基于参数优化MLOG与SAM的滚动轴承早期故障诊断

俞森， 马洁

(北京信息科技大学机电工程学院， 北京 100192)

0 前言

轴承被誉为“工业的关节”，在汽车、高铁、风力发电、冶金、化工、船舶以及大型制造业中广泛使用。但由于其在高压、碰撞、高温等复杂的工作环境极易发生损伤，在生产生活中，约1/3的机械设备损坏由轴承故障引起[1]。因此，如何更早地发现轴承故障并进行维修保养，对减少事故发生和降低经济损失非常重要。轴承故障诊断主要涉及2个任务：特征提取和故障分类[2-3]。

基于振动信号分析的故障诊断方法能有效诊断机械设备缺陷和破损[4]。受工作环境影响，振动信号特征往往被噪声覆盖[5]，因此，噪声处理是滚动轴承故障诊断中的关键问题之一。1980年，MARR 和HILDRETH[6]首次提出拉普拉斯高斯滤波器，被广泛应用于图像边缘检测问题中，但在振动信号中并没有得到好的应用；SAAD等[7]将拉普拉斯滤波器用于地震波去噪，计算地震波到达时间；LIU等[8]将teager能量算子和拉普拉斯高斯滤波器结合，用于变转速工况下的特诊提取，但滤波器参数需人为设定； SAM(Spectral Amplitude Modulation)由MOSHREFZADE等于2019年提出[9]，通过给原始信号赋予不同的权值重构信号，然后计算重构信号的平方包络谱寻找故障特征频率，但受噪声影响较大。因此，本文作者利用麻雀算法自适应地选择MLOG的最优参数，并结合SAM方法对信号重构，从而提取故障特征频率。

1 理论分析

1.1 拉普拉斯高斯滤波器

高斯滤波可用于消除高斯噪声，对图像噪声处理效果优异[10]，得到了广泛应用。由于图像由不同灰度级的像素组成，不同灰度级即可看作图像特征信息的突变，在轴承振动信号中，噪声信号和振动信号频率、相位、幅值等存在差异，采集同一时刻的故障信号可视为特征信息突变，因此，文中提出利用拉普拉斯高斯滤波器对振动信号去噪。

一阶高斯滤波函数定义式为

(1)

式中：σ为标准差；n为高斯指数。对式(1)求二阶导并将结果归一化得：

(2)

对于单位冲击响应滤波器，当系数之和为零时，噪声处理效果最优，此时可很好地提取信号的瞬态脉冲。式(3)为改进的拉普拉斯高斯滤波器数学表达式：

(3)

式中：N为滤波器的阶数。

1.2 麻雀搜索算法

麻雀搜索算法由XUE和SHEN[11]于2020年提出，是一种新的优化算法。通过模仿麻雀捕食行为，将种群分为发现者、加入者和预警者。发现者能量储备较高，负责搜寻食物；加入者跟随发现者捕食增加能量储备，当发现有危险靠近时，预警者预警，进行反哺食行为，此时发现者将所有麻雀引到安全区域。生产者为麻雀种群中随机选择能量储备最高的个体，但数量保持不变。

设n个麻雀搜索d维空间，麻雀位置表示为

(4)

麻雀的适应度值为

(5)

发现者位置更新公式为

(6)

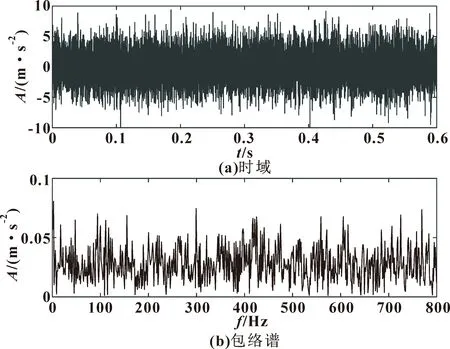
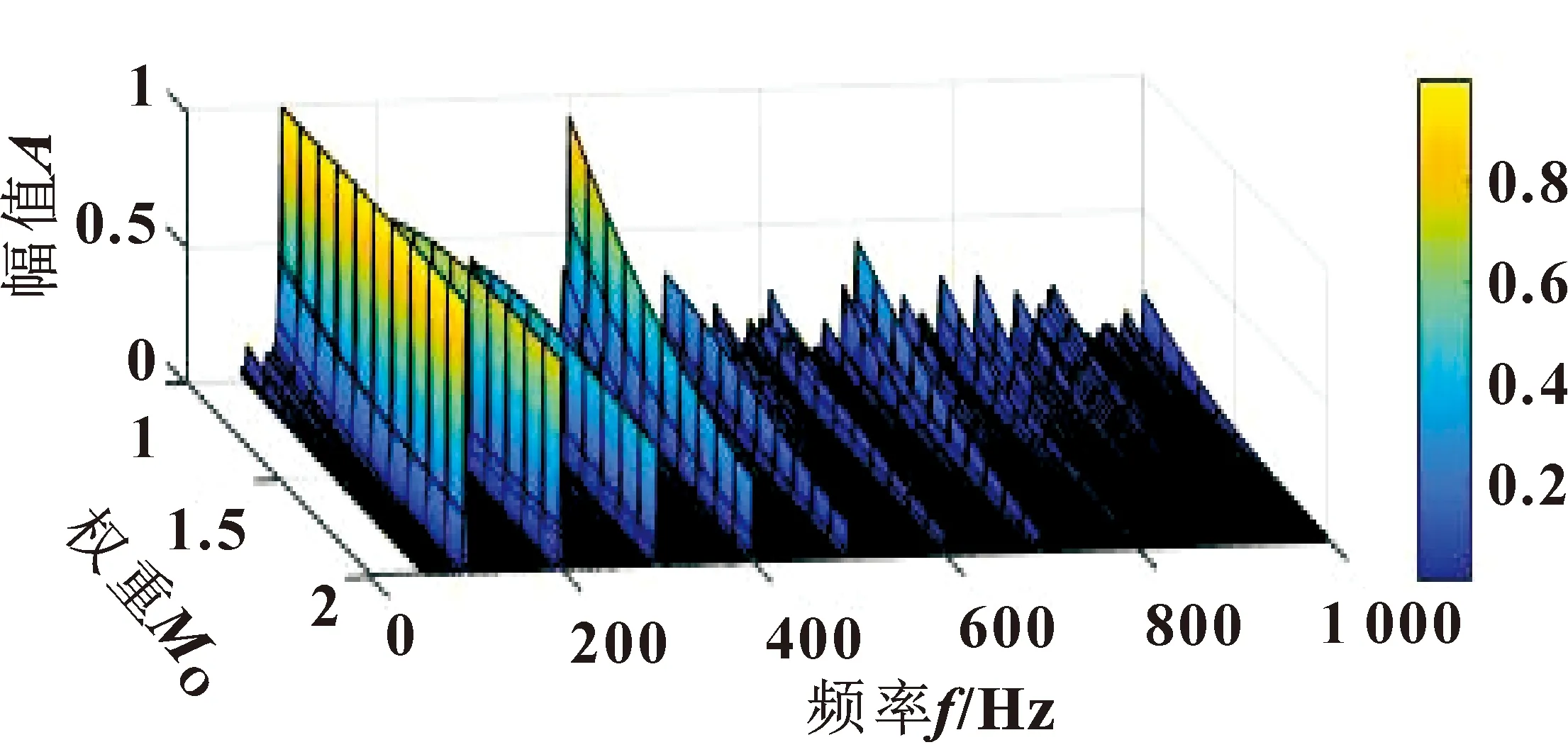
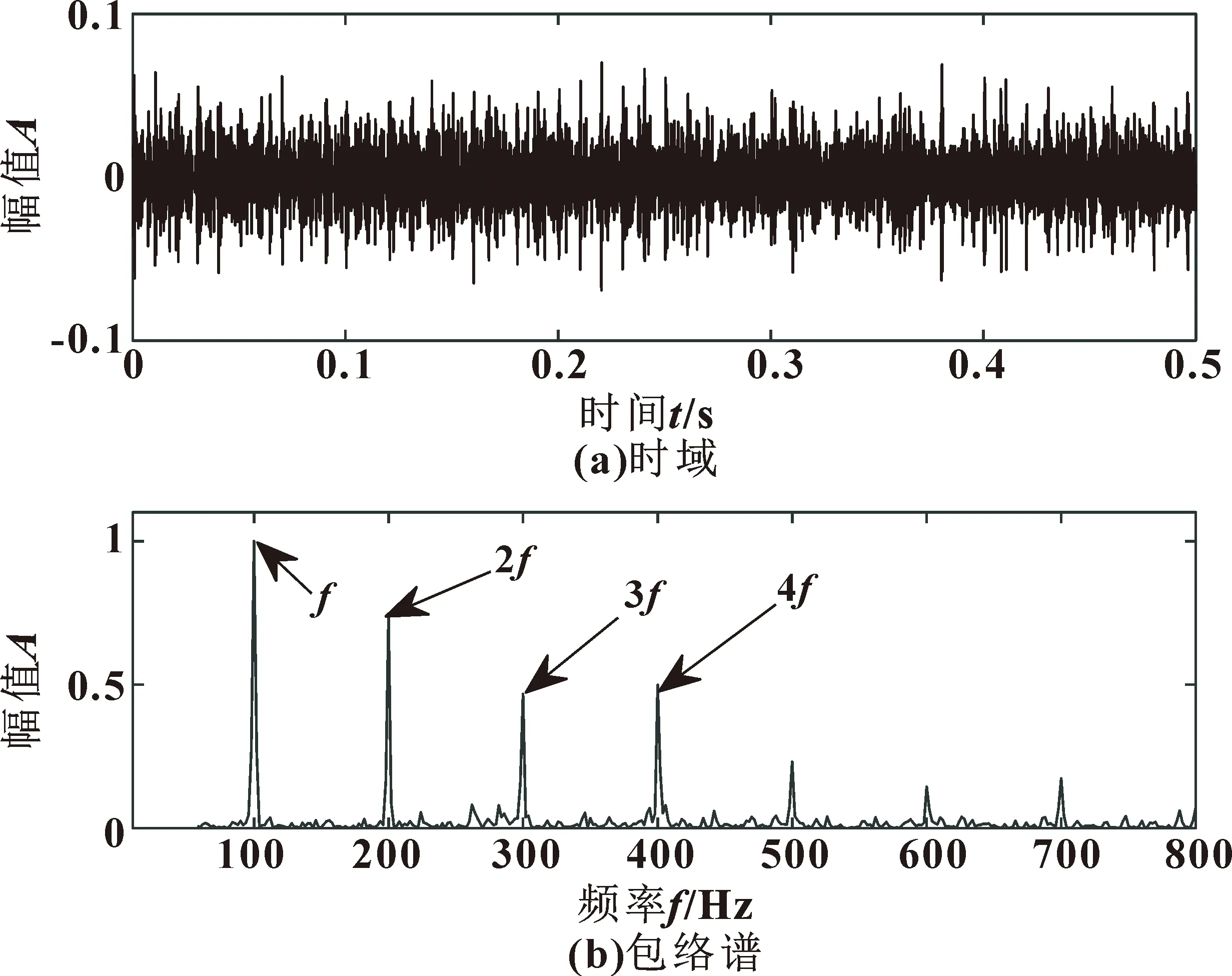
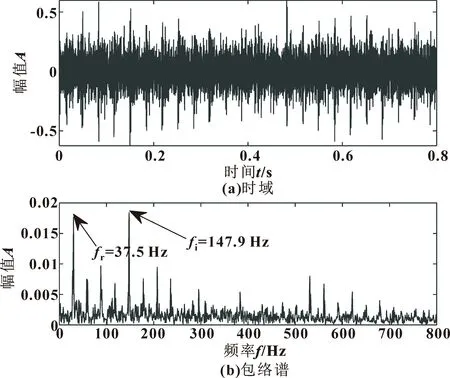
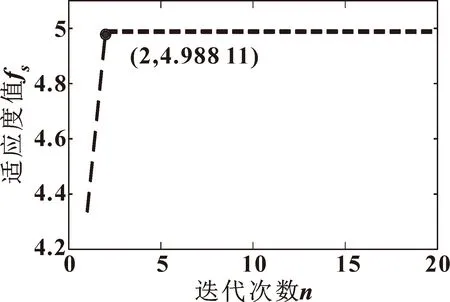
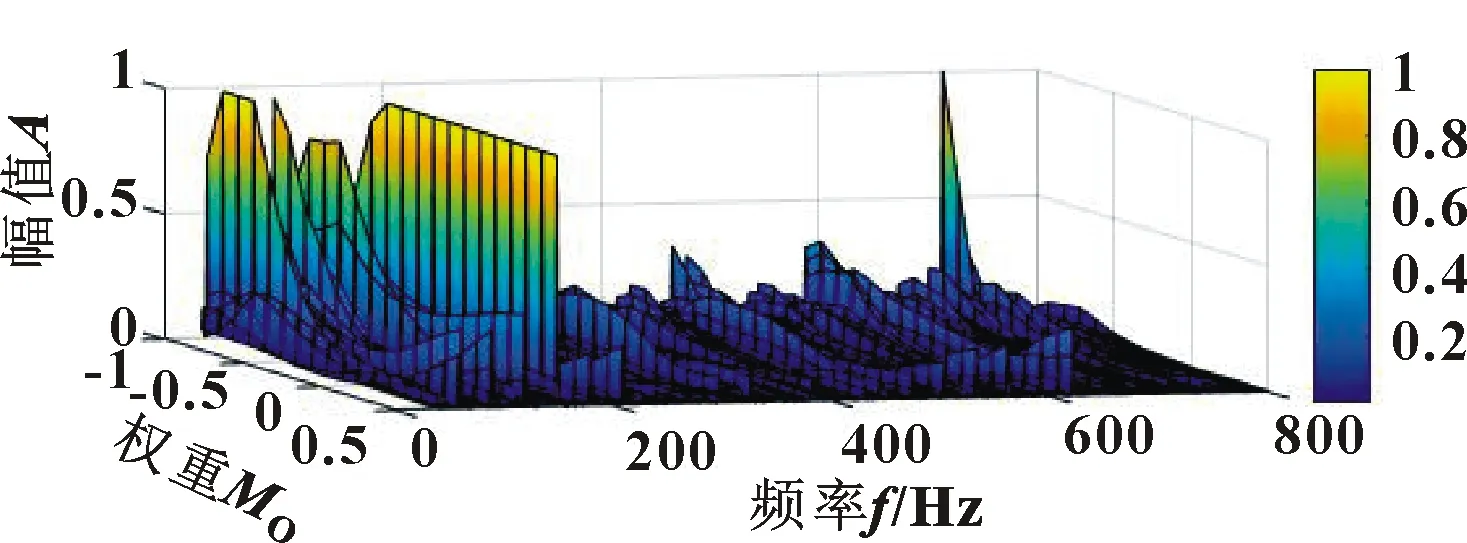
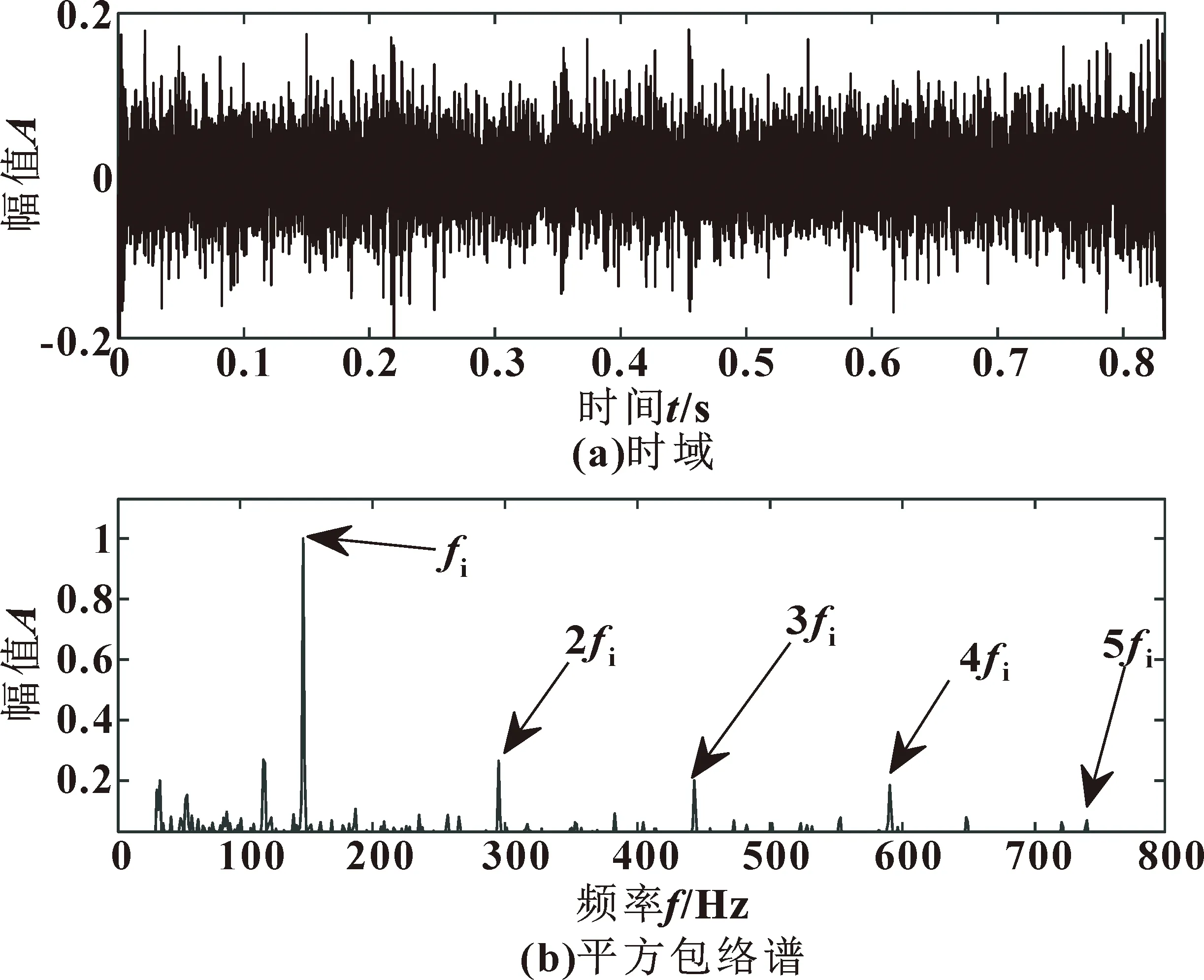
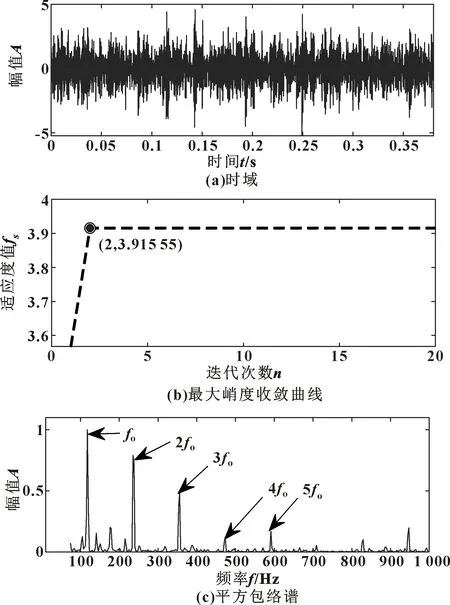
式中：t为当前迭代次数；tmax为最大迭代次数;α∈(0,1)；Q服从正态分布；I是元素都为1的1×d矩阵；R2∈(0,1)，ST∈(0.5,1)；R2

加入者位置更新公式为

(7)

式中：Xp和Xworst分别为当前发现的最优位置和全局中当前最差位置；A为1×d的矩阵，元素为1或-1随机分布，且A+=AT(AAT)-1。

随机选择麻雀总数的10%～20%作为预警者，位置更新公式为

(8)

1.3 频谱调幅(SAM)

在倒谱预白化过程中，由于单位幅度的任意设定而不能更好地表现频谱的特征，文献[12]中提出了倒谱预白化的新方法：

Xm(t,n)=IFT[A(f)nejφ(f)]

(9)

式中：Xm为重构信号；n为数量级。

均值为零的周期性信号x(t)的傅里叶级数表达式如下：

(10)

式中：D为傅里叶系数；q为信号x(t)的长度。

对x(t)做Hilbert变换，有：

(11)

计算原始信号的平方包络或范数，有：

cos[(ωi-ωj)t+φi-φj]

(12)

重构信号xm由x(t)的幅值和相位确定，则有：

(13)

计算xm的平方包络谱为

SES(fk,n)=(2-δ(k))·

(14)

2 麻雀算法优化MLOG数学模型

峭度与轴承自身属性无关，对冲击信号极其敏感，正常轴承峭度值为3。研究表明：峭度值会随轴承的损坏程度而逐渐增大，特别适用于早期故障的诊断问题。丁金玲等[13]以峭度最大值为标准选择小波包分解后的最优频带系数，准确提取特征频率。马晨佩等[14]利用麻雀算法搜索SVM的最优参数，有效解决了轴承的故障诊断问题。因此文中提出基于麻雀算法优化拉普拉斯滤波器的方法，以滤波后信号的峭度值为适应度函数，选择滤波器的最优参数，根据峭度最大值选择合适的滤波器参数，式(15)为峭度计算公式：

(15)

式中：x为振动信号；μ为均值；σ为标准差。

参数优化流程如图1所示，具体步骤如下：

(1) 输入故障信号，设置滤波器尺度参数和阶数N的上下界，初始化SSA算法的最大迭代次数和种群数量；

(2) 滤波器对故障信号滤波，根据式(15)计算滤波后信号的峭度并保存；

(3)判断是否达到终止条件，未达到则更新位置继续迭代。选择滤波后信号最大峭度值对应的N为最优参数；

(4) 用最优参数对原始信号滤波；

(5) 滤波后的信号用SAM处理，分析频谱特征，识别故障特征频率。

图1 故障诊断流程 Fig.1 Flow of fault diagnosis

3 仿真信号分析

为了验证文中方法的有效性，构造轴承故障时仿真信号如下：

y(t)=x(t)+n(t)

(16)

(17)

式中：x(t)为周期性冲击信号；n(t)为随机噪声信号；A为位移常数；ζ为阻尼系数；fn为轴承固有频率。

设故障冲击周期为T0=0.01 s，则故障特征频率为ft=100 Hz，采样频率f=20 kHz，采样点数N=10 000，令A=2，ζ=0.2，fn=2 000 Hz，n(t)是人为加入的高斯白噪声，此处信噪比SNR=-8 dB，图2所示为y(t)的时域和包络谱，从中无法识别任何故障成分。

图2 仿真信号

设置最大迭代次数20，种群数量10，滤波器阶数N∈[1,10]，标准差σ∈[0.1,5]，收敛曲线如图3所示，得到滤波器最优参数(N=10，σ=3)。

图3 仿真信号最大峭度收敛曲线

用选择的最优参数对信号用拉普拉斯滤波器滤波，将滤波后信号用SAM处理，设置1≤MO≤2，得SAM的三维图如图4所示。选择最高峰值对应的权重值MO=1.5对信号重构，重构信号的时域和对数平方包络谱如图5所示，可明显看到一倍频(100 Hz)及其他倍频成分，可判定轴承故障。

图4 仿真信号的SAMFig.4 SAM of simulation signal

图5 重构信号

4 实测数据分析

4.1 内圈故障数据分析

为验证文中方法的实用性，选取美国凯斯西储大学内圈故障数据进行验证，采用6203-2RS JEM SKF深沟球轴承，故障直径0.177 8 mm，轴承转速n=1 797 r/min，轴承参数见表1，根据公式计算得故障特征频率为fI=147.6 Hz。

表1 6203-2RS JEM SKF轴承参数Tab.1 Bearing parameters of 6203-2RS JEM SKF

采样频率fn=12 000 Hz，采样点数N=10 000，振动信号时域和包络谱如图6所示，可看出:转频fr=37.5 Hz，特征频率fi=147.9 Hz，与理论计算值基本一致，但其他倍频成分被噪声掩盖。

图6 内圈故障信号

设置麻雀算法最大迭代次数20，种群数量10，滤波器阶数N∈[1,10]，标准差σ∈[0.1,5]，收敛曲线如图7所示，迭代第2次得最大峭度值K=4.99，得最优参数(N=8，σ=2.24)。

图7 内圈故障信号最大峭度收敛曲线

用选择的最优参数对内圈信号用拉普拉斯滤波器滤波，将滤波后信号用SAM处理，设置-1≤MO≤0.5，得SAM的三维图如图8所示，选择最高峰值对应的权重值MO=-0.3对信号重构，重构信号的时域和对数平方包络谱如图9所示，可明显看出：一倍频及其他倍频成分与计算值接近，说明轴承内圈故障。

图8 内圈故障信号SAMFig.8 SAM of inner race fault signal

图9 重构信号

4.2 外圈故障数据分析

为再次验证此方法的有效性，选择西交大全生命周期故障数据进行验证[15]，轴承型号为LDK UER204，滚动轴承参数见表2，选择Bearing 2_5外圈故障数据集第120个样本，采样频率fn=25 600 Hz，转速n=2 250 r/min，根据公式计算得外圈故障特征频率为fo=115.6 Hz。

表2 LDK UER204轴承参数Tab.2 Bearing parameters of LDK UER204

外圈故障信号时域如图10(a)所示，用SSA-MLOG-SAM对信号处理，适应度函数的收敛曲线如图10(b)所示，得到滤波器最优参数(N=8，σ=1.87)。滤波后信号经SAM处理重构后的平方包络谱如图10(c)所示，可看到故障特征频率及其他倍频成分，证明轴承发生外圈故障。说明文中方法可准确识别不同试验台的不同故障类型。

图10 外圈故障信号分析

为表明麻雀算法优化滤波器参数的优越性，选择粒子群算法(Particle Swarm Optimization，PSO)和遗传算法GA对比验证，优化迭代曲线如图11所示。对比结果显示：麻雀算法在最少的迭代次数内达到最大适应度值，优于PSO和GA。

图11 不同算法优化滤波器参数迭代曲线

为表明拉普拉斯滤波效果的优越性，选择MCKD-SAM对内圈故障数据分析，设置滤波器长度L=160,移位数M=1，包络谱如图12所示，只能识别一倍频，其他倍频被淹没在噪声中。不对故障信号预处理，直接SAM后的包络谱如图13所示：从中只能识别一倍频和二倍频。对比结果显示：文中提出的方法对轴承早期故障特征提取更有效。

图12 MCKD-SAM包络谱Fig.12 Envelope spectrum of MCKD-SAM

图13 内圈故障信号SAM包络谱Fig.13 SAM envelope spectrum of inner race fault signal

5 结论

文中提出了SSA-MLOG-SAM的滚动轴承早期故障特征提取方法，通过仿真信号的不同试验台数据分析表明：

(1) 利用SSA算法自适应选择拉普拉斯高斯滤波器的最优参数，克服了人为设定参数的缺点，且优化效率高于传统粒子群算法和遗传算法；

(2) 验证了用于图像去噪的拉普拉斯高斯滤波器也能对振动信号去噪，且效果优于传统滤波方法；

(3)SAM利用非线性滤波分离信号成分，对滤波后信号赋予特定的权重来重构信号，通过平方包络谱分析准确地提取受强噪声干扰的故障特征频率，为滚动轴承的故障诊断提供了新的解决方法。