基于固定位姿约束的双目相机标定研究
2023-02-28张辉杨育陈瑶齐小龙
张辉,杨育,陈瑶,齐小龙
(江苏科技大学机械工程学院,江苏镇江 212003)
0 前言
双目视觉系统具有广泛应用,如三维测量和重建[1-3]、机器人导航[4-5]、航空航天工程[6-7]等。目前,用于相机标定的方法有多种。特别是ZHAO等[8]提出的利用标定板进行标定的方法,近年来得到广泛研究。许多研究集中于特征点的精确提取和参数优化模型上。ZHU等[9]提出了一种基于最优极化信息的方法来解决标定板图像中高亮区域的影响。谢佳奇等[10]提出一种基于改进风驱动算法的摄像机标定优化方法,该方法与张正友标定法相比具有更快的收敛速度和更好的稳定性。陈文艺等[11]针对平面目标的单目视觉标定过程复杂、标定精度不高的问题, 采用均方误差和最小原理对光心的位置坐标进行估计,并建立虚拟摄像机模型实现原图像的畸变校正。
在双目视觉系统中,2个相机间的相对关系在立体校正中起着重要的作用。双目视觉系统中仅仅对2个相机分别进行标定,无法保证在不同视角下相机之间的约束关系固定。郑顺义等[12]利用相机之间固定的相对位姿关系建立约束方程,并加入平差误差方程。杨伟姣等[13]考虑到观测点坐标提取误差,利用数字图像相关性对控制点坐标进行精确提取,并考虑相机之间关系建立约束方程,但优化模型的构建较为复杂,需从多方面考虑约束条件。
为获得高精度的标定结果,本文作者提出一种基于圆型图案标定板的双目相机标定新方法。采用数字图像相关法[14],从圆形图案的整体特征中提取特征点坐标。根据相机成像模型,建立涉及相机间固定约束关系的简化优化方程。该方法只需对其中一个相机的外部参数进行优化,就可保证2个相机在刚性位置关系的前提下获得更高的优化精度。
1 双目相机模型
相机成像模型通常用针孔模型[15]来描述。如图1所示,相机成像过程中涉及到的坐标系共有4个,分别是世界坐标系(WCS)、相机坐标系(CCS)、图像坐标系(ICS)和像素坐标系(PCS)。WCS中的一个点与PCS中的对应点之间的映射关系可以用数学方法描述为
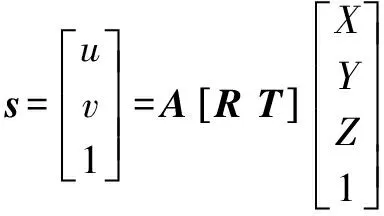
(1)
其中:s是比例因子;A是相机的内参矩阵;R和T分别表示从WCS到CCS的旋转矩阵和平移向量,也被称为相机的外部参数。
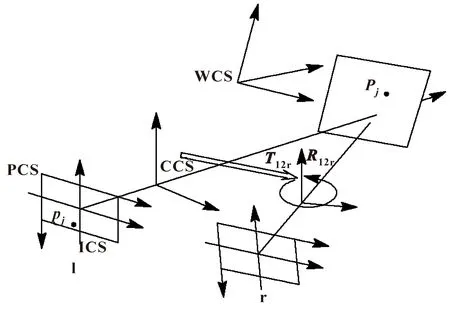
图1 针孔模型中的相机坐标系统Fig.1 Camera coordinate system in pinhole model
为了获得高精度的校准结果,需要考虑各种畸变引起的误差。造成误差的主要原因是径向畸变和切向畸变。因此系统的非线性失真模型定义如下:
(2)
其中:(x,y)为CCS中畸变点p的坐标;(xcorrect,ycorrect)为CCS中校正后点p的坐标;k1、k2、k3是描述径向畸变的系数;p1、p2是描述切向畸变的系数。另外,在双目相机系统中,2个相机之间的相对位置有如下变换关系:
Xl=Rl2rXr+tl2r
(3)
其中:Rl2r和tl2r分别是旋转矩阵和从右CCS到左CCS的平移向量;Xl和Xr分别表示左侧CCS和右侧CCS中的点的坐标。
2 标定方法
2.1 初始参数值估计
圆形目标的特征点是圆的中心点。传统的方法是利用圆形图案的边缘特征来拟合特征点的位置[16]。边缘检测用于获取圆形图案的边缘信息,然后通过椭圆拟合的方法计算像素点pj(u,v)的位置。给定控制点Pj(X,Y,Z),通过优化以下目标函数得到相机参数的初值A0:
(4)
其中:M为控制点从WCS到PCS的投影;m为从标定板图像中计算出的控制点个数。
2.2 特征点的精度提高
虽然椭圆拟合法可以检测原始图像中特征点的位置,但受到镜头和透视畸变的影响,圆形图案的中心坐标会偏离原来的位置。龚思宇[17]提出以Shi-Tomasi角点提取算法得到的特征点作为初始值,然后结合二次多项式逼近法的原理对特征点进行优化的方法,具有良好的抗噪声性能和鲁棒性。为了获得高精度的特征点像素坐标,文中提出了当标定板平面平行于相机成像平面的特定姿态的标定板前视图像。前视图像与标定图像的关系如图2所示。利用数字图像相关技术(DIC)将标准模板图像(由计算机生成的无畸变无噪声图像,且尺寸大小在图像坐标系下与真实图像一致)与前视图像进行匹配,得到两者之间的位移关系。
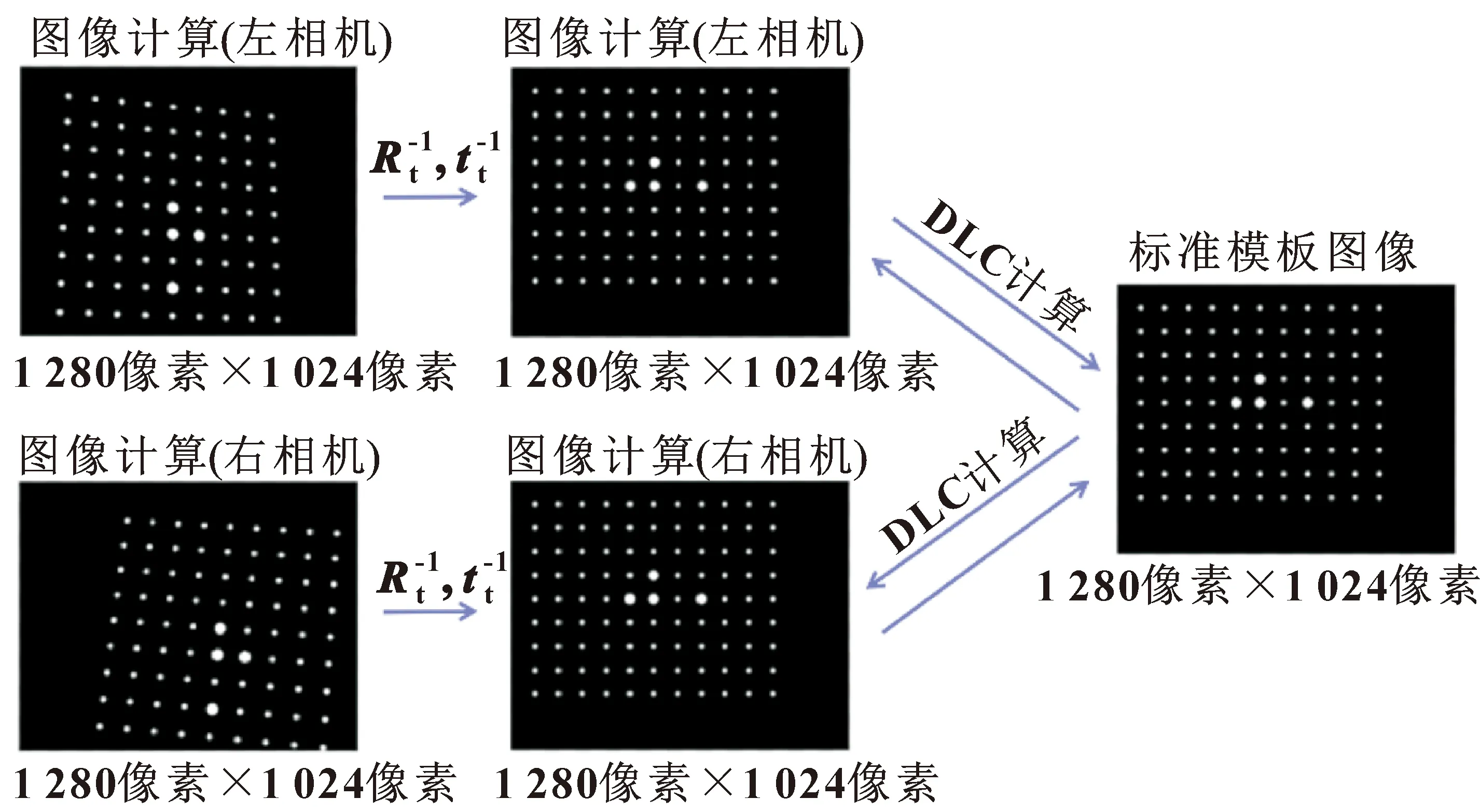
图2 前视图像与标定图像的关系
由于标准模板图像中特征点的像素坐标已知,在得到位移关系后可以准确地得到前视图像中特征点的坐标。相关形状函数为
(5)

∇C(s)=∇C(s0)+∇∇C(s0)(s-s0)=0
(6)
将上式改写为:∇∇C(s0)(s-s0)=-∇C(s0),其中s0为初值,s为迭代后的近似值,(s-s0)为单次迭代后的增量。∇∇C(s0)是相关函数的二阶偏导数,通常可构造为Hessian矩阵[19]。使用Newton-Raphson算法时涉及到亚像素位置的像素值。因此,有必要对前视图像的非整数位置进行插值。双三次插值具有良好的像素值平滑性和灰度梯度性,其插补形式如公式(7)所示:
G(x*,y*)=a00+a01y′+a02(y′)2+a03(y′)3+
a10x′+a11(x′)(y′)+a12(x′)(y′)2+a13(x′)(y′)3+
a20(x′)2+a21(x′)2(y′)+a22(x′)2(y′)2+a23(x′)2(y′)3+
a30(x′)3+a31(x′)3(y′)+a32(x′)3(y′)2+a33(x′)3(y′)3
(7)
其中:G(x*,y*)为插值点的灰度级;a00为像素(x,y)的灰度级;其余系数可通过在节点位置的一阶导数和交叉导数在相邻曲面之间连续的条件求得。插值点处的像素值为该像素在4像素×4像素的周边场中的权值。该插值方法考虑了4个相邻点对灰度的影响以及相邻点灰度变化率的影响。(x*,y*)是一个非整数像素点,x*在i和i+1之间,y*在j和j+1之间。
2.3 参数优化
优化上一节计算的特征点的新像素坐标,对左右相机重新标定。此时,只得到了单相机的内部和外部参数,尚未得到用于描述相机之间固定位姿关系的参数。此外,采用通用的单目相机优化方法对左右相机的参数进行独立优化时,由于没有考虑固定位置关系的因素,左右相机的固定位置关系参数仍然会有较大的误差。
因此,文中提出了一种基于固定约束关系的双目相机参数优化方法。根据两相机之间的位置关系,建立双目相机的重投影目标函数如下:
(8)
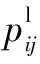
3 实验
3.1 仿真实验
通过仿真实验和实际实验对文中提出的标定方法进行了验证分析。通过计算机合成图像的大小为1 280像素×1 024像素,并加入了不同密度的高斯噪声。为了表明该方法的优越性,将该方法与传统的椭圆拟合方法进行了比较。采用椭圆拟合技术的方法称为method I,文中提出的方法称为method II。双目相机的内部参数和相对位置参数设置如下:
畸变参数被人为设置为0。为了保证标定结果的收敛性和准确性,使用10幅标定板图像来模拟双目相机在各个视角下所捕捉到的图像。
通过透视变换得到相应的标定板图像。将平均值为0、标准偏差σ从0到8每次间隔1像素的高斯噪声分别添加到这些图像中。在每个高斯噪声水平下,实验重复进行20次。采取2种方法,分别对左右相机进行标定,相对位置参数为各视角下计算的平均值。2种比较方法通过公式(8)优化相机参数,得到的相关内外参数校准结果如表1和表2所示,得到的平均重投影误差如图3所示。

表1 不同噪声水平下的双目相机内部参数 单位:像素

表2 不同噪声水平下双目相机的相对位姿参数Tab.2 Relative pose parameters of binocular cameras under different noise levels
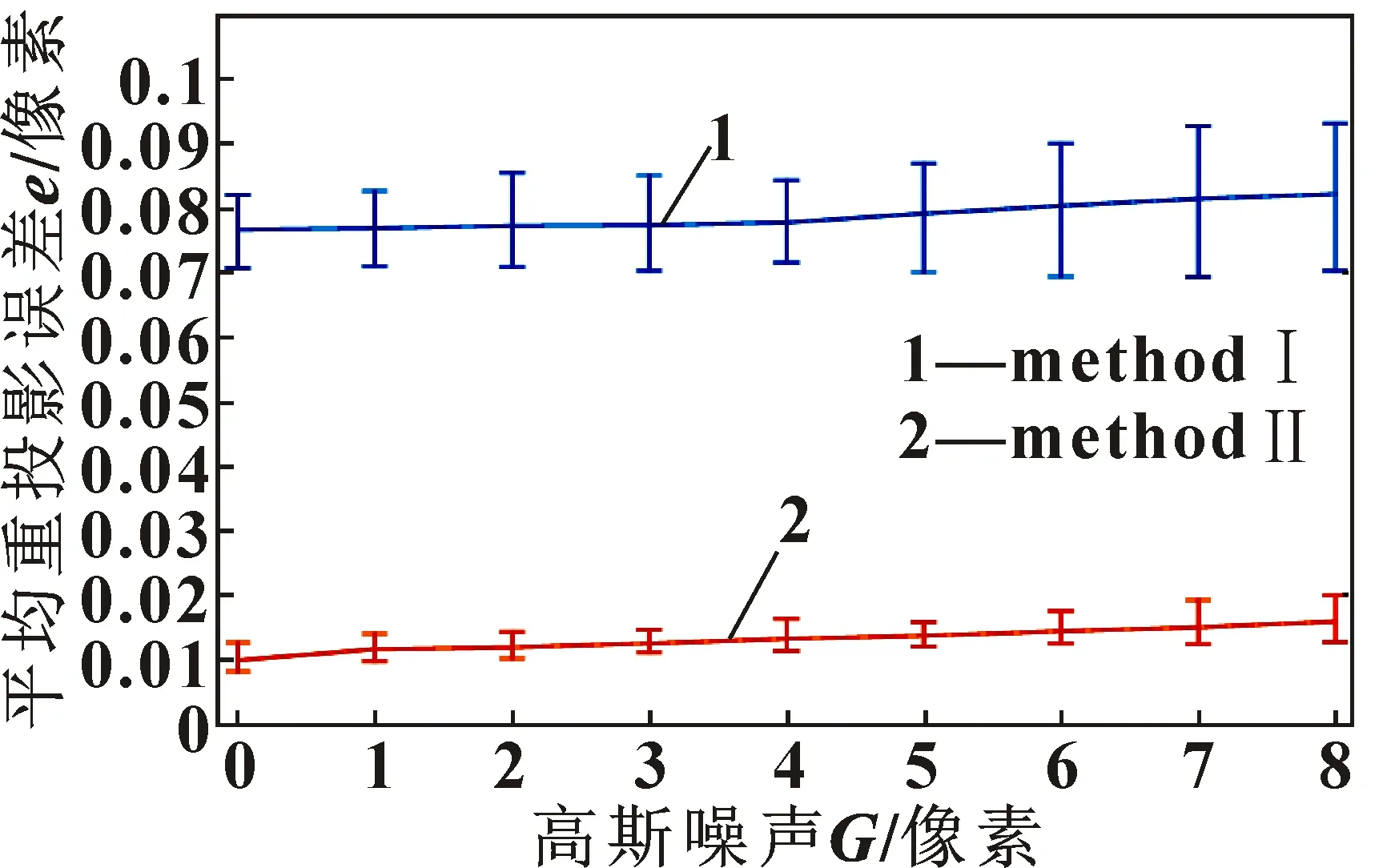
图3 双目相机平均重投影误差Fig.3 Average re-projection error of binocular camera
在固定约束条件下,2种方法的平均重投影误差分别为0.08像素与0.015像素左右。值得注意的是,当高斯噪声水平从0上升到8时,椭圆拟合方法和文中提出的方法得到的平均重投影误差都有所增大,其波动范围也有所增大。相比之下,在不同的噪声密度下,应用数字图像相关可以显著降低重投影误差。
3.2 实际实验
在实际实验中,使用2台工业相机OKIO-B-400组成的视觉系统进行双目标定。每个摄像头的分辨率为1 280像素×1 024像素。99个圆形图案(9×11)均匀分布的标定板,相邻的圆形图案的中心在水平和垂直方向上的距离均为30 mm(如图4所示)。

图4 带有99个圆形图案的校准板Fig.4 Calibration plate with 99 dot patterns
使用双目相机在不同视角下采集10对标定板图像,分别对左右摄像头进行标定,相对位置参数为各视角下计算的平均值。分别通过椭圆拟合法和数字图像相关法校正,再用公式(8)优化相机参数,校准结果见表3,得到的平均重投影误差如图5所示。

表3 真实实验的内外参数Tab.3 Internal and external parameters of real experiment

图5 优化后各视角的平均重投影误差
从图5可以看出:通过与使用椭圆拟合法获取特征点像素坐标的方法比较,利用文中提出的方法在降低重投影误差方面表现出了很好的效果。但是,由于相机制造精度、畸变因素、周围光照的影响以及相机参数初始设定不完整等原因,实际实验的精度无法达到仿真精度的水平。
4 结束语
(1)文中提出了一种基于固定位姿约束的高精度双目相机标定方法,并对校正后的相机相关参数进行了评价,仿真和实际实验验证了该方法的有效性。
(2)仿真结果表明:随着图像中的高斯噪声水平提高,使用椭圆拟合方法和文中提出的方法得到的平均重投影误差都有所增大,其波动范围也有所增大。相比之下,在不同的噪声密度下,应用文中提出的方法可以显著降低重投影误差。
(3)实际实验结果表明:该方法的平均重投影水平相比采用椭圆拟合法降低了25%左右,证明了该方法有效,并且可以推广到更多的相机上。
