基于球面线性插值的机器人磨削工具姿态规划

毛文志，潘通，李程鹏，徐金亭

(1.大连理工大学汽车工程学院，辽宁大连 116024；2.沈阳新松机器人自动化股份有限公司，辽宁沈阳 110168)

0 前言

汽车轮毂作为汽车的重要零部件，不仅影响着汽车行驶性能及安全性，同时还对汽车的车型定位、外观差异性及使役过程中的车辆性能等产生重要影响[1]。在轮毂制造中，轮毂坯件边缘通常存在翻边及毛刺等表面缺陷[2]。为保证轮毂最终的表面质量和使役性能，必须去除轮毂边缘的翻边及毛刺。目前，在汽车轮毂打磨过程中，通常会采用人工打磨或机器人人工示教磨削来完成翻边及毛刺的去除[3]。人工打磨的加工效率低、加工质量严重依赖工人的经验，而人工示教也存在着人力消耗大、灵活性及自动化程度不高、平稳性差等问题[4]。因此，为提高汽车轮毂磨削的加工效率及自动化程度，必须对机器人磨削工具姿态进行自动规划，以期在磨削过程中机器人末端工具姿态变化更加平顺，从而保证轮毂表面质量，并使磨削工具磨损更加均匀，满足大批量加工的生产要求。

目前，机器人磨削工具姿态的自动规划主要采用五轴数控加工中的刀轴矢量规划方法。对五轴刀轴矢量规划而言，PLAKHOTNIK和LAUWERS[5]采用迪卡斯特算法，对五轴机床的旋转轴角度进行优化，使得机床旋转轴在运动过程中变化最小。罗明等人[6]提出对刀轴矢量的角度变化进行约束，在保证加工不发生干涉的前提下，对刀轴矢量进行光顺。XU等[7]给出了五轴机床的逆向运动学变换关系，并基于此提出了相应的刀轴矢量光顺性指标。张平等人[8]提出用三次均匀样条四元数插补算法来构造刀具姿态过渡曲线，实现了工业机器人任务空间姿态平滑过渡。陈爱文等[9]提出基于正弦加减速控制的四元数球面线性插值的姿态轨迹规划算法，构建出姿态平滑的七自由度串联机器人位姿轨迹。HO等[10]利用四元数插值对五轴加工中的刀轴矢量进行优化，获得了变化均匀、光顺的刀轴矢量。HUANG等[11]则是将径向基函数插值应用到刀轴矢量的规划当中，完成了光顺刀轴矢量的优化。与四元数插值及径向基函数插值相比，球面线性插值具有实现简单、计算效率高等优点[12]，而且能够获得角速度变化均匀的中间矢量，避免了在复杂加工路径下末端执行器角度跃变损坏机器人关节电机的情况。

为此，本文作者将采用球面线性插值对末端执行器工具姿态进行规划，将离散路径拟合为B样条曲线，通过对样条路径关键区域中关键点处工具姿态间的球面线性插值，生成沿磨削路径光顺变化的工具姿态，从而保证磨削过程中的机器人末端执行器运动的平稳光顺。

1 离散路径的预处理

通过激光测量获得的轮毂内孔边缘路径点是散乱无序的，无法直接用于后续加工，必须对其进行序化处理。为此，给出如下的散乱点序化方法：

(3)基于第2步中的比较准则，通过快速排序算法完成散乱路径点的序化处理；

(4)完成路径点的有序化处理后，采用3次B样条曲线对其进行最小二乘拟合：

(1)

式中：di为B样条曲线控制顶点；Ni,3(u)为B样条基函数。拟合得到的轮毂内孔边缘B样条曲线如图1所示。

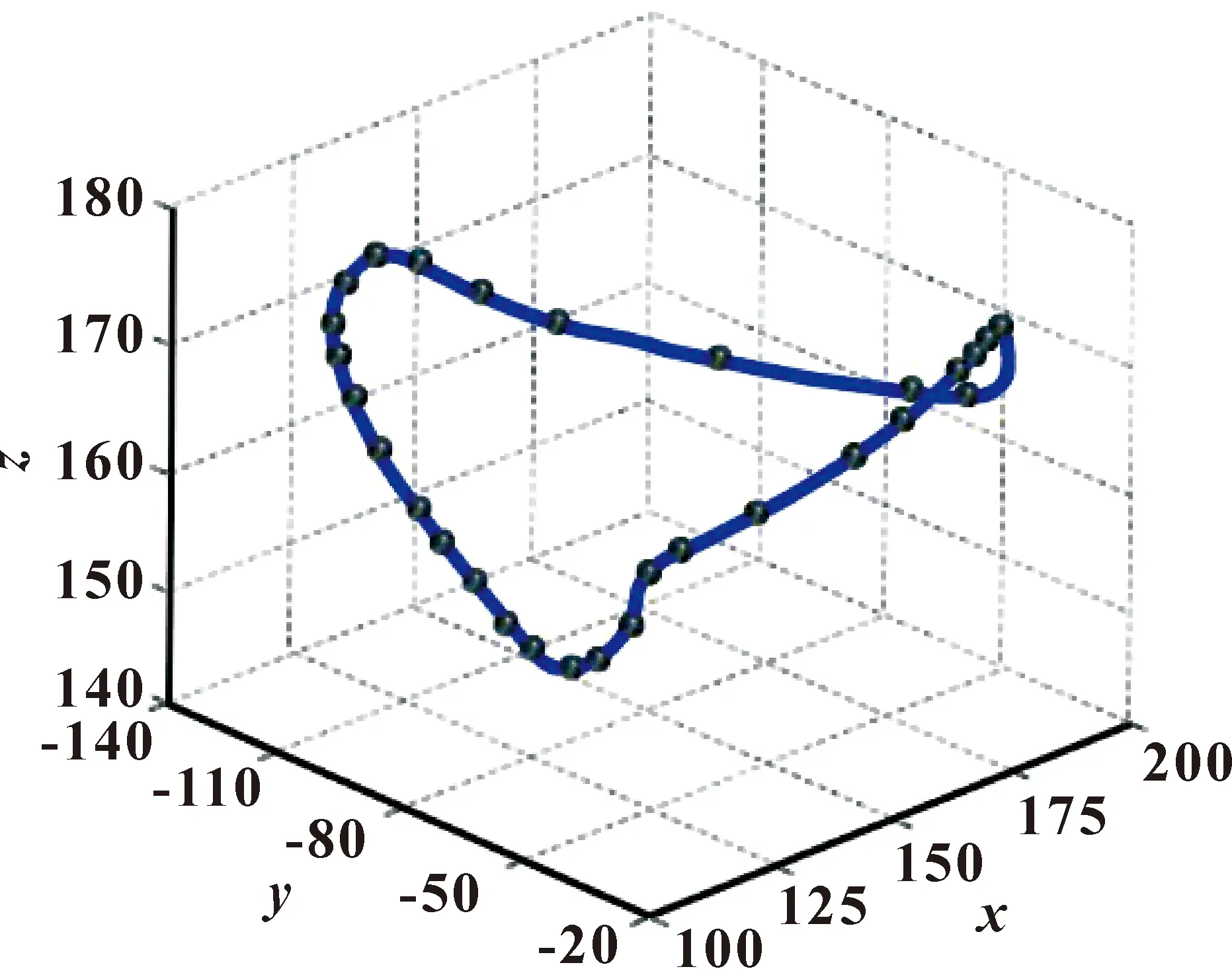
图1 B样条拟合的轮毂内孔边缘曲线Fig.1 Wheel inner hole edge curve fitted by B-spline

2 关键区域及关键点的识别

文中选取路径曲率κ作为衡量路径变化的参数，用于关键区域及关键点的选取。曲率计算公式如下：

(2)

式中：B样条路径的各阶导矢可由公式(3)计算：

(3)

设曲率阈值为κlimit，文中κlimit=0.02。曲率大于κlimit的点被认为是关键区域内的点，如图2红色所示，其他点则为非关键区域点。轮毂边缘曲线曲率分布及关键区域分割结果如图3所示。将关键区域的两边界点及区域内曲率最大点设定为关键点。

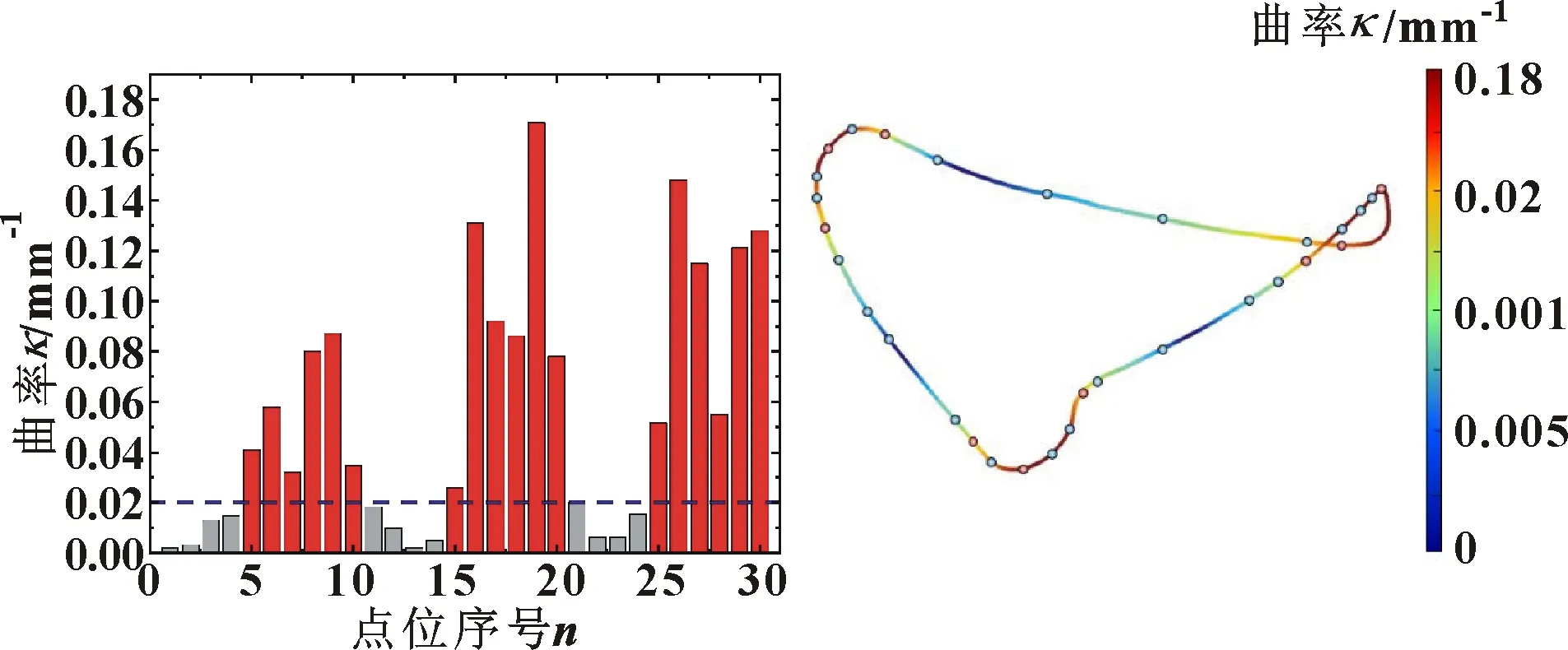
图2 各个拟合点的曲率分布 图3 识别出的关键区域与关键点

3 磨削工具姿态规划

文中将在机器人的任务空间进行磨削工具姿态规划。所谓磨削工具姿态即为机器人末端坐标系中Z轴矢量ze。ze将通过对末端坐标Y轴矢量ve的调整来重新规划，以保证工具姿态变化的光顺性。末端坐标系Z轴沿着磨削工具方向，正方向指向工件，Y轴初始为样条路径切矢量也是姿态规划过程中的优化对象，X轴由Y轴和Z轴按照右手法则确定。

3.1 切向过渡优化

关键点处末端坐标系切向(Y轴)矢量可简单设置为该点处的切矢量，也可由人机交互指定。然后，就可通过关键点处切矢量间的球面线性插值生成中间点的Y轴方向矢量，获得变化光顺的工具姿态。球面线性插值的公式如下：

(4)

(5)

式中：ut为姿态插值点的参数值。

这样，就可根据关键点序列，将加工路径分成若干段。在每一段首末工具姿态的切向矢量间进行球面线性插值，生成中间点处工具姿态的切向矢量。优化后的末端坐标系Y轴如图4所示，可以看到路径变化更为光顺。但优化后Y轴可能与Z轴不再垂直，需要根据优化后的Y轴对末端坐标系进行重新规划：

(1)求出上述球面插值过程产生的vt与Z轴方向矢量ze的叉积w，w=vt×ze；

(2)以w的方向作为新的X轴，vt的方向作为新的Y轴，w×vt为Z轴，即规划后的工具姿态，构建出新的机器人末端坐标系。

图4 优化前(a)与优化后(b)效果对比

3.2 Z向位置浮动

(6)

式中：σt为线性插值得到的中间路径点处的浮动量。利用上述方法就可生成所有点的Z向浮动值。

4 实例验证

为验证所提出的机器人磨削工具姿态规划算法的有效性，进行模拟仿真和实验验证。在实验中，优化前末端坐标系的Y轴方向是路径切线方向且不予以磨削位置点任何浮动。所分析的磨削工具姿态运动学参数为运动过程中Y轴的角度差及角速度差的波动。轮毂实际磨削实验如图5所示。优化后的角度差变化曲线、角速度差变化分别如图6、图7所示。可以看出：角度差和角速度差的波动与优化前相比明显降低。分别计算其标准差，可以得到角度差的波动程度比优化之前降低了22.28%，角速度变化的波动程度比优化之前降低了40.43%。

图5 轮毂实际磨削实验

图6 优化前后角度变化对比

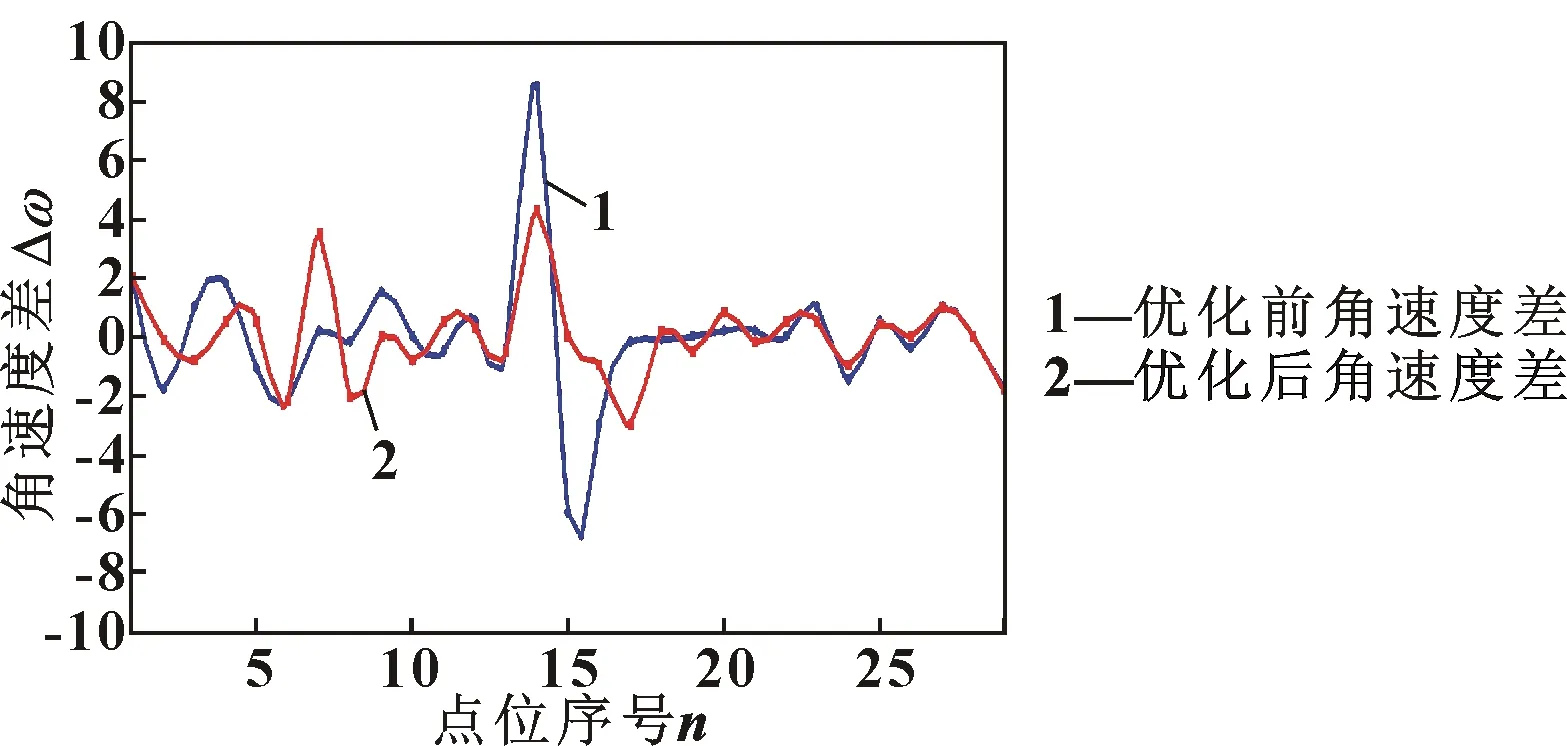
图7 优化前后角速度变化对比

5 结论

文中针对目前轮毂磨削中所规划工具姿态灵活度不够、平稳性差等问题，提出一种基于球面线性插值的机器人磨削工具姿态规划方法，并进行了模拟仿真和实际加工实验。实验证实所提方法能够产生变化更为光顺的工具姿态，优化后工具姿态角度波动降低22.28%，角速度波动降低40.43%，能够保证磨削过程更为光顺。此外，Z向位置浮动的引入使得轮毂边缘磨削更为均匀，能够有效减少工具磨损。在后续研究中，将结合动力学对磨削工具姿态规划进一步优化，以期得到更加顺滑、平稳的磨削工具姿态和更好的磨削效果。