新能源场站分布式同步调相机暂态功角失稳形态及机理
2023-02-27杨松浩李秉芳赵天骐
杨松浩,李秉芳,赵天骐,赵 伟,徐 鹏,谢 欢
(1. 西安交通大学电气工程学院,陕西省西安市 710049;2. 华北电力科学研究院有限责任公司,北京市 100045;3. 国家电网有限公司华北分部,北京市 100053)
0 引言
随着“双碳”战略的实施,大规模新能源集中送出的新格局逐步形成。然而,新能源集中送出系统动态无功支撑能力较弱,电压稳定性问题凸显,极大限制了新能源基地的外送能力[1-2]。
同步调相机作为一种动态无功补偿装置,在提升系统短路比、增强系统电压和频率稳定性等方面独具优势[3-4]。目前,国内外已开展了一系列同步调相机与新能源发电组合的相关研究[5-7]。结果表明,此种组合可作为一种新形式电网支撑型电源,有助于缓解送端系统暂态过电压、抑制故障暂态中新能源大规模脱网并提升新能源输送比例。《国家电网有限公司构建以新能源为主体的新型电力系统行动方案(2021—2030)》明确了推广新能源场站部署调相机来提高新能源场站对电网的短路容量支撑能力[8]。未来,同步调相机将在支撑新型电力系统建设和促进新能源消纳方面起到更重要的作用。
然而,同步调相机在提升送出系统电压稳定性的同时,也会对系统的功角稳定性构成潜在威胁。一般而言,同步调相机静稳裕度很大,发生功角失稳的风险较低,因此相关研究较少。文献[9]阐述了位于负荷中心的同步调相机减速失步现象及影响因素,但并未深入分析其失稳机理。关于更加广义的同步电动机功角稳定问题,现有研究集中在大扰动下电动机转子转矩平衡被破坏后发生减速失稳现象[10-11]。
实际上,新能源场站同步调相机的功角稳定性分析可借鉴新能源影响下的同步系统暂态稳定性相关结论。文献[12]将新能源有功功率等效为系统的机械功率,基于扩展等面积定则阐述系统功角失稳机理。文献[13-14]基于直流潮流模型提出了风电接入后两机系统暂态功角稳定性判据,并定性地分析了风电场选址、同步机出力和风电渗透率等因素的影响规律。文献[15]进一步将此判据扩展运用到了多风电场电力系统。文献[16]研究了风机外特性及单端送电系统的功率特性方程,认为随着风电出力的增大,系统功角稳定性会先提升后降低。
对于新能源场站中的同步调相机,由于新能源与调相机的强耦合性,调相机在故障过程中有发生暂态失稳的风险。文献[17]研究了新能源与同步调相机联合系统在其送出断面故障造成的孤岛运行模式下调相机功角加速失稳风险,并从短路比角度分析了其失稳机理及影响因素。这是首次明确指出同步调相机暂态加速失稳现象的研究,但其仅讨论了远区故障下新能源保持恒功率输出的场景,未研究发生近区故障、触发新能源低电压穿越(low voltage ride-through,LVRT)等更复杂、更具一般性的场景。针对这一问题,本文提出了一种考虑新能源故障暂态的同步调相机暂态稳定性分析方法。首先,通过网络化简和系统等值,构建了考虑新能源功率注入的调相机暂态稳定性分析模型;然后,分析了新能源故障暂态影响下调相机的转子运动过程和功角失稳形态,基于等面积定则揭示其失稳机理,并提出暂态失稳判据;最后,通过实际新能源送出系统的简化模型和IEEE 39 节点改进模型,仿真验证了理论分析的准确性。
1 新能源场站分布式调相机暂态功角稳定性分析模型
本文构造的含同步调相机的新能源送出系统拓扑结构如图1(a)所示。其中,新能源代表风电场或光伏电站,同步调相机与新能源电源经同一母线并入电网,并与远端同步系统构成了典型的两机系统。

图1 含调相机的新能源送出系统Fig.1 Renewable energy sending-end power system with condenser
为简化分析,本文采用以下假设:
1)新能源采用电流源模型,故障穿越期间有功输出下降,故障清除后恢复至稳态水平;
2)远端同步系统采用大容量的同步发电机模拟,同步发电机和调相机均采用经典二阶同步机模型;
3)暂态过程中不考虑同步发电机调速器的作用;
4)负荷采用恒阻抗模型;
5)不考虑频率变化对网络参数的影响。
基于上述假设,将该两机系统简化等值为单机无穷大系统。图1(b)为两机系统的等值电路图。图中,E1和E2分别为调相机、发电机的暂态电势;Zd1和Zd2为 暂 态 阻 抗;ZT1和ZT2分 别 为 变 压 器1、2的等值阻抗,ZL为线路等值阻抗;ZL1为新能源内阻抗、并网变压器阻抗及输电线路对地支路阻抗的等值阻抗;ZL2为线路末端负荷阻抗及输电线路对地阻抗的等值阻抗。
该两机系统的功角摇摆方程为:

式中:PM1和PM2分别为调相机、发电机的机械输入功率;PEC和PEG分别为调相机、发电机的电磁输出功率;M1和M2分别为调相机、发电机的惯性时间常数;δ1和δ2分别为调相机和发电机自身的功角。
定义相对功角δ=δ1-δ2,得到调相机相对于系统的摇摆方程为:

式中:Meq、PM和PE分别为两机系统等值惯性时间常数、机械功率和电磁功率。为获得PE的表达式,可消去图1(b)的中间节点,只保留同步机内电势节点1 和2[18-19],如 图1(c)所 示。详 细 推 导 过 程 见 附录A。
图1(c)中,y′11、y′12和y′22为化简后系统的导纳参数,表达式见附录A 式(A7)。I1和I2分别为节点1、2 的输出电流;I′0和I″0分别为新能源电流I0经化简后等效在节点1、2 注入的电流。其表达式为:

式中:y11和y12为化简过程中的导纳参数,表达式见附录A 式(A3)。
由式(6)可知,新能源发电可等效为两个分别注入同步调相机和发电机节点的电流源,其分配系数与网络参数有关,节点注入电流的幅值与新能源总出力I0成正比。从物理意义上来讲,新能源电流加入系统后,其有功功率根据电气距离影响各同步机节点的旋转动态(见附录A 式(A8))。I′0和I″0的大小实际反映了各同步机对功率注入源的敏感程度。
由图1(c)中网络列节点电压方程可得:

式 中:ϕ12为Y12的 幅 角;G11、G12和G22分 别 为Y11、Y12和Y22的实数部分。
需要指出的是:1)图1 中同步调相机的变量定义采用发电机惯例,在电动机视角下,只改变调相机电气量的正方向,不改变其暂态功角特性;2)式(1)至式(12)的推导具有一般性,网络拓扑发生变化时,只需更新式(7)中的导纳矩阵,即可获得准确的电磁功率曲线。当系统发生不对称短路故障时,可根据正序等效定则在网络故障处接入相应的附加阻抗,再更新导纳矩阵进行计算,过程与前述一致。
2 新能源基地调相机功角失稳形态及机理
2.1 新能源注入功率对调相机稳定运行点的影响
调相机相对于系统侧的稳定运行点是稳态时等值机械功率PM曲线与电磁功率PE曲线的交点。新能源的出力可通过改变PM和PE曲线的相对位置从而改变调相机功角稳态稳定运行点。
1)新能源功率对PM的影响
调相机没有原动机,稳态运行时只吸收少量的有功功率用以自身损耗,而发电机稳态时需供给有功负荷,即PM1≈0,PM2>0。由式(4)可知,稳态时PM<0,且假设其在暂态过程中保持不变。新能源的注入使发电机稳态出力减小。根据式(4),PM随之增大,进而导致调相机的静态稳定裕度变小。
2)新能源功率对PE的影响
由式(8)可知,新能源注入后调相机PE方程中增加了P″E项。 调相机的惯量较小,一般有M1 下面对调相机在故障暂态中的功角失稳形态展开研究。 图2(a)和(b)分别为不同新能源LVRT 深度下的调相机暂态等值功角特性曲线。图中,PE1、PE2和PE3分别为短路前、短路中、短路清除后调相机等值功角;红色、绿色阴影部分为加速面积,蓝色阴影部分为减速面积。LVRT 深度为0 表明故障期间新能源出力不变,LVRT 深度为90%表明故障期间新能源出力降低90%,即只保留10%有功输出。 图2 新能源LVRT 深度较低/较高的暂态过程分析Fig.2 Transient process analysis of low/high LVRT depth of renewable energy 1)新能源LVRT 深度较低 调相机初始稳定运行点为a点,对应的相对功角为δ0,随I0的增大而右移。当发生短路时,Pem因两机间的电气距离增大而减小,使得PE2曲线的幅值减小。在新能源LVRT 深度较低时,故障期间有功电流出力降幅不大,所以虽然PE2曲线会略微上移,但在短路过程中PE2 2)新能源LVRT 深度较高 当新能源的有功出力在故障期间显著降低时,短路中虽然Pem减小,但此时新能源出力的大幅减少会使得P″E较稳态时增大,从而使PE2相对上移,所以有PE2>PM,如图2(b)所示。下面详细分析调相机的功角摇摆情况。 (1)故障前 稳态运行点为a点,即PE1与PM的交点。 (2)故障期间 运行点a→b→c:由于PM (3)故障清除后 运行点c→d→e:由于PM>PE3,调相机开始加速。但在此期间,调相机转速小于发电机,相对功角会继续减小,直到到达e点两机同速。 运行点e→d→h:PM>PE3,调相机相对于发电机开始加速,功角开始增大。 运行点h→i→j:PM 对于上述机电暂态过程,可采用等面积定则进行稳定性判别。在新能源LVRT 深度较低时,调相机功角摇摆过程与传统同步机基本一致,暂态稳定/失稳的机理和判据也与之相同。在此暂态过程中,加速面积S+为由a、b、c、h这4 点围成的面积Sabch,即S+=Sabch,最大减速面积为Smax-=Shij。 当新能源LVRT 深度较高时,调相机在到达不稳定平衡点j之前经历了先减速、再加速、后减速的3 个阶段。整个暂态过程中加速面积为Sdefg+Sefh,最大减速面积为Sabcg+Shij。不考虑能量损耗,在运行点由b到c的过程中,调相机相对于发电机的动能减少量等于从d到e的动能增量,所以有Sabcg=Sdefg。因此,可用于稳定性判别的加速面积为: 式中:δh、δe、δj分别为运行点h、e、j所对应的功角。 根据等面积定则,若S+ 在Power Factory/DigSilent 中搭建含调相机的新能源送出系统简化模型如附录B 图B1 所示。仿真模型中线路、风机和主网同步机参数均根据冀北锡盟地区白音查干汇集站实际电网等值而来,可以较为准确地反映实际工程中调相机和风机的动态过程。 1)元件参数 新能源采用风力发电机模型,不同运行方式下风机、调相机和发电机的容量及惯量参数见表1。 表1 元件参数Table 1 Component parameters 2)故障设置 故障设置为0.5 s 时线路2 的一回线50%处发生三相永久性短路,100 ms 后保护动作将故障线路切除。故障期间,在LVRT 深度较高和较低两种情况下,穿越深度分别为90%和10%。故障切除后风机有功出力全部恢复。 在上述参数和故障设置下,分别针对新能源LVRT 深度较低/较高两种情况进行了仿真,得到的调相机等值功角、转速ω和相轨迹曲线如图3 所示。从图3 可见,新能源LVRT 深度的不同导致相轨迹在故障期间(运行点a→d)的动态存在差别。调相机初始功角稳定运行点均为a点,若LVRT 深度较低,则故障持续期间δ和ω都增大(a→d);反之,则都减小。故障清除后,方式1 下调相机经阻尼振荡稳定在新的运行点s(d→h→m→s);方式2 下δ先减小(d→e)后增大(e→j),最终调相机相对于系统失去同步。 图3 LVRT 深度较低/较高时两种运行方式下功角、转速和相轨迹Fig.3 Power angle, rotate speed and phase trajectory when LVRT depth is low or high with two operation modes 图4 给出了方式1、2 下新能源LVRT 深度较低/较高时新能源送出系统时域仿真功角特性曲线对比。其中,红色部分为加速面积,蓝色部分为减速面积,暂态仿真结果与理论分析一致。不同运行方式及LVRT 策略下的加减速面积计算结果见表2。方式1 下,不论LVRT 深度的高低均有S+ 表2 不同运行方式及LVRT 策略下的暂态稳定性仿真结果Table 2 Transient stability simulation results under different operation modes and LVRT strategies 图4 LVRT 深度较低/较高时两种运行方式下功角特性曲线Fig.4 Power angle characteristic curves when LVRT depth is low/high in two operation modes 为验证新能源场站分布式调相机在多机系统中的暂态功角失稳风险,构建了改进的IEEE 39 节点系统如附录B 图B2 所示。与标准系统相比,改进系统将母线38 的850 MV·A 同步发电机更换为同容量的风电机组,并配备了250 MV·A 的同步调相机接在母线40。扰动设置为线路28-29 的50%处发生三相短路故障,故障持续100 ms 后切除故障线路。故障清除后新能源功率恢复至稳态水平。 针对表3 所设计的4 种场景分别进行仿真,得到的调相机功角随时间的变化曲线如图5 所示,等值暂态功角特性曲线见附录B 图B3。 表3 4 种场景及相应暂态稳定性结果Table 3 Four scenarios and corresponding transient stability results 从图5 可知,当新能源稳态有功出力为850 MV·A 时(场景1 和2),调相机经暂态扰动后保持功角稳定。当稳态出力增至950 MV·A 时(场景3 和4),出现了调相机暂态功角失稳的现象。当LVRT 深度较低时(10%),调相机在短路阶段功角直接增大;而在LVRT 深度较高时(90%),调相机则呈现出功角先减小后增加的暂态功角稳定/失稳形态。上述仿真结果与理论分析一致。 图5 4 种场景下新能源送出系统等值功角Fig.5 Equivalent power angle of renewable energy sending system in four scenarios 针对新能源场站同步调相机的暂态功角稳定性问题,本文提出了一种考虑新能源暂态影响的调相机稳定性分析方法,主要结论包括:含调相机的新能源基地在故障暂态中,新能源发电以电流源形式分别向调相机和等值系统节点注入功率,使调相机具有暂态功角加速失稳的风险;在不同的新能源故障穿越深度控制策略下,调相机呈现不同的功角振荡形态。本文所提方法揭示了新能源送端同步调相机的加速失稳过程和物理机理,理论上能够量化分析控制及网络参数对调相机失稳的影响,后续可为新能源送出系统的配置及运行控制提供理论指导和参考。但是本文结论是在一定假设条件下获得的,而实际场景中新能源的暂态特性及耦合因素更加复杂,需要在此基础上开展更加深入的研究。 本文研究获得了华北电力科学研究院科技项目(KJZ2022035)的资助,特此感谢! 附录见本刊网络版(http://www.aeps-info.com/aeps/ch/index.aspx),扫英文摘要后二维码可以阅读网络全文。2.2 暂态功角失稳形态分析
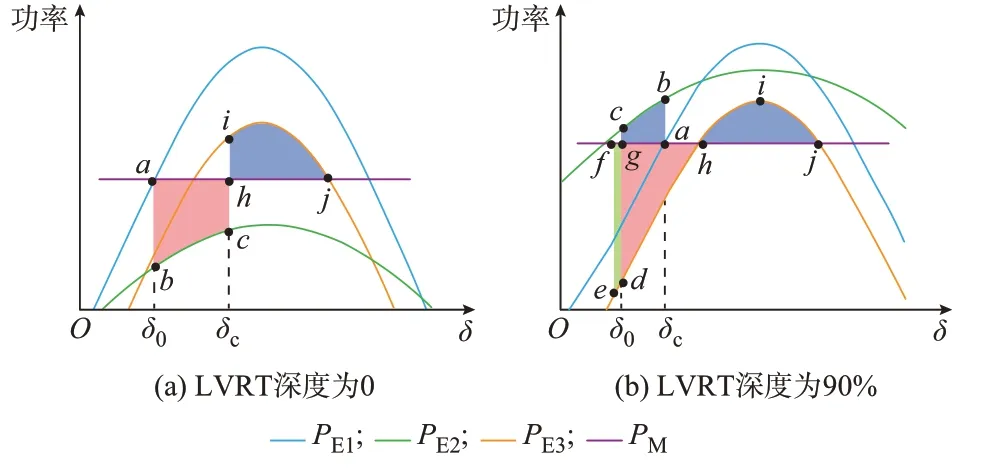
2.3 暂态功角失稳机理与失稳判据

3 仿真验证
3.1 新能源送出系统简化模型

3.2 简化系统仿真结果



3.3 IEEE 39 节点改进系统

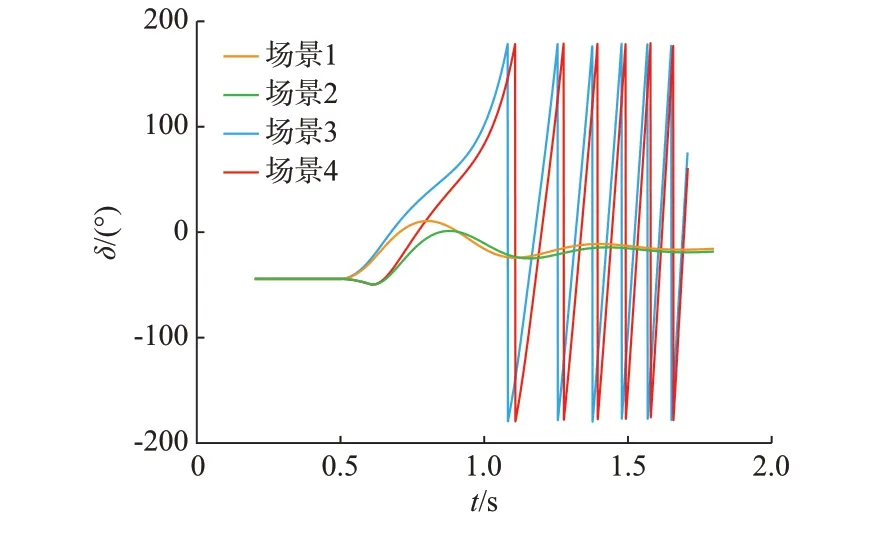
4 结语
