基于可观性分析和多步预报CKF 的双馈风机动态状态估计

朱茂林，刘 灏，毕天姝

（新能源电力系统国家重点实验室（华北电力大学）,北京市 102206）

0 引言

在落实“碳达峰·碳中和”目标的大背景下,风电的开发与利用必然会越来越受到重视。近年来,中国风力发电量迅速增长,但大规模风电接入电力系统会对电网的安全稳定运行产生影响［1］,需要实时获取并监测其运行状态。动态状态估计（dynamic state estimation,DSE）可以利用电网和电力元件的模型、参数以及实时遥信遥测数据,如同步相量测量装置（synchrophasor measurement unit,PMU）的数据,求解电力系统实时运行状态,并降低量测噪声及滤除不良数据,因此,DSE 对监测风力发电机的运行状态具有重要意义。基于双馈感应发电机（doubly-fed induction generator,DFIG）的风力发电机（以下简称“双馈风机”）因其良好的经济性和运行特性已成为风电场主力机型之一,本文选择其作为DSE 的研究对象。

卡尔曼滤波作为主要的DSE 方法［2-5］,本质上是一种数据融合的手段,即利用实际量测对系统模型预报值进行修正,因此,DSE 的结果受到量测的影响。不同量测集对应状态估计结果的收敛速度和准确性差异较大,即不同量测集对应的系统可观性不同［6］。文献［7］基于线性化方法研究了系统矩阵特征值对同步发电机状态可观性的影响。文献［8］利用线性化和Lie 导数这2 种方法分析了同步发电机的可观性,发现Lie 导数的分析结果更加准确。文献［9］采用经验可观测格兰姆矩阵来评估含发电机在内的整个系统的可观性水平。然而,上述文献都是以传统同步发电机为研究对象。目前,针对双馈风机的DSE 研究［10-11］大多基于风电场等值模型和风电场出口处的相量量测,且对于量测的选择都是简单指定。然而,风电场动态特征较同步发电机更为复杂,难以用单台风力发电机等值模型表征。此外,只基于风电场出口相量量测很难满足状态估计可观性的要求。随着风电场分布式能量管理系统（energy management system,EMS）的发展［12］,出现了针对新能源电源的PMU［13］,使得对风电场内单台风力发电机进行动态状态估计成为可能,且可提供更多的量测选择。因此,基于单台风力发电机模型,研究不同量测集对应的状态可观性,进而选择使双馈风机状态最可观的量测量,对实现高效准确的双馈风机动态状态估计很有必要。

目前针对风力发电机的DSE 方法中,文献［10］介绍了双馈风机的详细模型,并以此为基础比较了扩展卡尔曼滤波和无迹卡尔曼滤波的估计效果。文献［11］进一步将无迹卡尔曼滤波与粒子滤波相结合,以提高双馈风机状态估计的精度。但上述文献仅是将不同的卡尔曼滤波方法应用于双馈风机的状态估计,未针对双馈风机的实际特点进行改进。文献［14］考虑到实际中风速可能未知的情况,先估计未知风速再进行状态估计,使结果更具实用性。与同步发电机相比,双馈风机容量小且包含转子、直流电容、交流绕组和滤波电感等储能元件［15］,同时还采用快动态的电力电子装置来进行控制。因此,双馈风机的状态变量在扰动后变化迅速。通常,DSE的估计步长由PMU 量测上送速率决定,一般为25～100 Hz。对于时间常数较小的状态变量,此步长会导致卡尔曼滤波的状态预报向量不准确,进而导致DSE 的结果不收敛。

针对上述问题,本文首先基于Lie 导数推导非线性系统的可观性矩阵,并利用最小奇异值（smallest singular value, SSV）作为衡量系统可观性的指标,选出使双馈风机具有较高可观性的量测集；然后,提出基于多步预报的容积卡尔曼滤波（cubature Kalman filter,CKF）方法,通过减小预报步长减小离散误差,并根据预报误差估计值自适应确定多步预报参数；最后,利用修改后的IEEE 39 节点系统进行测试,验证所提算法的有效性。

1 双馈风机模型及量测分析

双馈风机模型主要由机械部分、电气部分以及控制系统组成。其中,机械部分包括风轮及传动系统、异步电机的转子；电气部分包括定子绕组、转子绕组、转子侧变流器和网侧变流器；控制系统包括转速控制、转子侧和网侧换流器控制等。双馈风机的结构图及详细动态模型见附录A,此处用动态系统的一般状态空间形式表示,如式（1）所示。

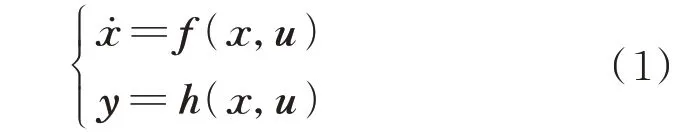
式 中:f为 系 统 函 数；h为 量 测 函 数；y为m维 量 测 向量；x=［ωr,ψdr,ψqr,ψds,ψqs,Udc,idg,iqg,x1,x2,x3,x4,x5,x6,x7］T为 双 馈 风 机 的n维 状 态 向 量,其 中,ωr为发电机转子角速度,ψdr和ψqr分别为转子绕组磁链Ψr的d轴、q轴分量,ψds和ψqs分别为定子绕组磁链Ψs的d轴、q轴分量,Udc为直流电容电压,idg和iqg分别为网侧换流器交流侧电流Ig的d轴、q轴分量,x1,x2,…,x7为双馈风机转子侧和网侧控制器中积分环节的状态变量,其定义就是实测值与给定参考值之间差值的积分,具体表达式见附录A,控制框图见附录A 图A2；u=［Vw,uds,uqs］T为输入向量,其中,Vw为 风 速,uds和uqs分 别 为 定 子 电 压Us的d轴、q轴分量。

传统EMS 是一种以控制中心为核心的集中式管理系统。在这种集中式系统中,为了降低模型复杂程度,通常对风电场进行等值建模,而目前多数风电场只在与系统连接处装有PMU。因此,双馈风机的DSE 一般基于风电场聚合模型［10-11］,可用量测仅限于风电场出口数据,如式（2）所示。

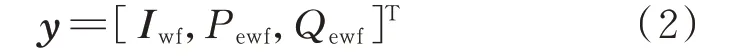
式中:Iwf、Pewf、Qewf分别为风电场与电网连接处的电流、有功功率和无功功率。

风电场分布式EMS 可以有效提高风电利用效率,其以风电场的精细化网络模型和实时测量量为基础［12］,能够准确感知风电场内部的运行状态,但仅风电场出口处的量测难以满足可观性要求。因此,需要对风电场内双馈风机加装量测装置。现已有针对新能源系统的PMU［16］,增加了DSE 的可用量测,故本文基于上述分析对单台风力发电机DSE进行研究。

结合相关标准［17］,确定在对单台双馈风机进行状态估计时的备选量测如式（3）所示。

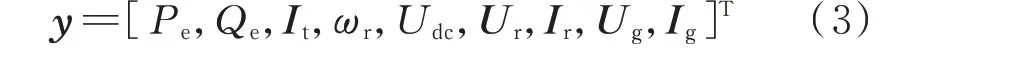
式中:Pe和Qe分别为双馈风机输出的有功和无功功率；It为双馈风机输出电流；Ur和Ir分别为转子电压和电流；Ug为网侧换流器的交流侧电压。

式（3）给出了本文对双馈风机进行估计时的备选量测,但目前并非所有风电场都能满足这样的量测条件,且从状态估计的角度来看,并不是所有量测对DSE 都是必要的,需要通过可观性分析来进行量测集的系统选择,同时减少量测需求以提高DSE 的适用性。

2 可观性矩阵计算及评价指标

对于式（1）所示动态系统,输入控制量u通常假设已知,输出y可直接由量测装置获得,而系统的状态变量x大部分无法通过直接测量获得,需要通过估计得到,而DSE 能否准确估计系统状态则受量测集可观性的影响。

2.1 可观性定义及可观性矩阵

可观性定义:对于如式（1）所示动态系统,如果对任意给定的输入u,在有限观测时间［t0,tf］内,根据［t0,tf］期间的输出y（t）能唯一确定系统在初始时刻t0的状态x0,则称状态x0是可观的。若系统的每一个状态都是可观的,则称系统是完全可观的。系统的可观性反映了通过有限时间内的量测确定系统状态的能力。可观性分析可在进行状态估计之前分析确定最佳量测集,为DSE 量测集的选择提供依据。对于线性定常系统:

式中:A为系统矩阵；B为输入矩阵；C为输出矩阵。

状态x可观的充分必要条件为:式（5）中可观性矩阵O͂的秩等于状态向量维数n［18］。

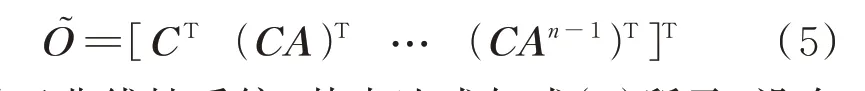
对于非线性系统,其表达式如式（1）所示,没有对应的矩阵A和C,无法按式（5）计算可观性矩阵O͂。最直接的方法是将非线性系统线性化,但简单线性化会引入较大的截断误差［8］。因此,考虑采用Lie 导数来计算非线性系统的可观性矩阵。

可观性表示的是输出反映状态的能力,与控制作用u没有直接关系,所以分析可观性问题时可忽略输入。式（1）所示的非线性系统可表示为:

式 中:Ω为y0到y(p-1)组 成 的 列 向 量；h1(x),h2(x),…,hm(x)为式（1）中m维量测函数h的组成元素。

如果映射Θ是可逆的（即单射）,则可以从输出y重建状态［19］。因此,考察该映射的Jacobian 矩阵,即可观性矩阵O͂的奇异性就可判别系统的可观性,O͂如式（12）所示。

2.2 O͂的计算及可观性评价指标

在确定双馈风机的量测集和动态方程后,就可以计算可观性矩阵。然而,由式（12）可知,Lie 导数的计算涉及高阶求导,具体到双馈风机模型,其状态向量维数n=15,意味着最高要算14 阶Lie 导数,手工计算或使用常规符号计算工具求解非常耗时。自动微分（automatic differentiation,AD）技术根据微分计算的链式法则,将微分定义为代数运算,不需要推导导数计算公式就可以自动计算函数的微分,且不含截断误差,克服了上述缺点［20］。ADOL-C［21］是基于C++语言开发的AD 系统,能够计算任意阶导数,且该工具能够处理条件语句,非常适用于双馈风机这种高阶模型。因此,选择该工具进行双馈风机可观性矩阵的计算。利用ADOL-C 计算不同量测集下的双馈风机可观性矩阵的步骤如下所示。

1）输入双馈风机参数和仿真数据。

2）为AD 申请空间,声明活跃变量,包含自变量x,用于存储状态变量的值；因变量f（x）,用于存储双馈风机的系统方程；因变量y,用于存储不同量测集的量测方程。

3）将双馈风机状态向量的数值传递给活跃变量x,并写出f（x）和y的具体表达式,即式（1）。

4）调用lie_gradient 函数,得到y（x）关于f（x）的Lie 导数矩阵,即式（12）中的O͂。

由于可观性矩阵O͂的计算与系统状态有关,可观性分析结果是时变的,且结果也不是简单的可观或不可观［6］,为此选择O͂的最小奇异值作为评价可观性的指标。可观性矩阵O͂的奇异值分解如下:

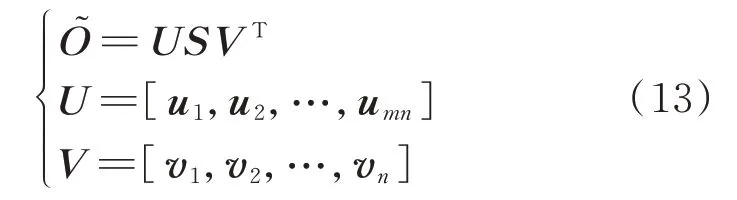
式中:U和V分别为左奇异矩阵和右奇异矩阵,均为正交阵,ui和vi分别为其第i个列向量；S=diag（δ1,δ2,…,δn）,为奇异值矩阵,其中,diag 表示求对角矩阵的函数,δi为O͂的奇异值,且δ1>δ2>…>δn,δn即为最小奇异值,其值的大小代表了O͂的奇异程度。

对于给定的量测集,可观性矩阵的SSV 越大,表示系统状态可观性越好。由于非线性系统的可观性是局部性质,可观性矩阵的SSV 将随着状态向量x的变化而变化。

3 基于多步预报的CKF

3.1 离散误差与多步预报

在确定测量量后,就可以利用卡尔曼滤波进行状态估计。PMU 量测数据属于离散采样,且状态估计和控制算法经常在数字电路中实现,因此,需要把式（1）中连续时间的动态系统转化为离散形式。对式（1）中微分方程在［tk-1,tk］内积分得:

式中:tk-1和tk分别为第k-1 个和第k个离散时间；xk-1和xk分别为第k-1 个和第k个离散时间的状态向量。

通过式（14）和式（15）就可将离散问题转化为积分问题。由数值分析可知,可以从2 个方面减小积分结果的误差:一是采用高精度的数值方法；二是减小步长λ。

首先,为了平衡计算复杂度和精度,本文采用2 阶精度的改进欧拉法［22］得到离散模型:

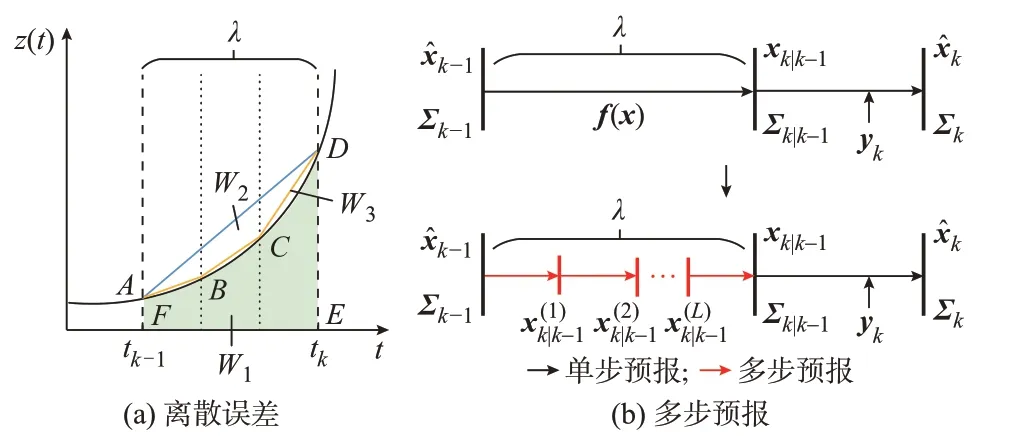
图1 离散误差和多步预报示意图Fig.1 Schematic diagram of discretization error and multi-step prediction

3.2 自适应确定参数L

得到预报误差后便可确定L:设置容许误差ε,若将原步长λ分为L段,则步长变为λ/L,由于改进欧拉法是2 阶精度,因而理论上预报误差应除以L2,故可利用式（19）确定L的值:

3.3 多步预报CKF 步骤

基于上述分析对CKF 进行改进得到多步预报CKF,具体步骤如下:

步骤1:初始化。设定初始时刻状态值x̂0、状态估计误差协方差矩阵Σ0和初始输入u0为稳态运行值,设定过程和量测噪声协方差矩阵Λ和β,令k=1。

4 仿真验证

基于修改后的IEEE 39 节点系统对双馈风机的备选量测进行可观性分析并选出最佳量测集,然后检验所提多步预报CKF 方法的效果。加入双馈风机的IEEE 39 节点系统拓扑见附录A 图A3,双馈风机的参数见附录A 表A1,IEEE 39 节点系统的详细参数见文献［23］。线路28-29 在t=1.5 s 时发生断线故障,t=2.5 s 时故障清除,量测采样间隔为0.02 s,仿真时长8 s。将时域仿真获取的双馈风机相关电气量作为真实值,在真实值基础上添加噪声作为量测,过程和量测噪声的协方差矩阵Λ和β设定为10-6γn×n和10-8γm×m,γ表示单位矩阵,容许误差ε设 为10-4。

4.1 不同量测集的可观性分析

式（3）列出了对双馈风机进行状态估计时的备选量测,将这些量测分别单独作为一个量测集,计算对应的可观性矩阵,以研究量测对双馈风机状态可观性的影响。由于Pe和Qe都是视在功率的分量,将其同时作为量测的情况也考虑在内。此外,考虑双馈风机所有状态量都可直接测量这一理想量测集,用xDFIG表示以方便结果比较。仿真过程中,各量测集对应的SSV 均值如表1 所示,各量测集SSV 随时间的变化情况如图2 所示。

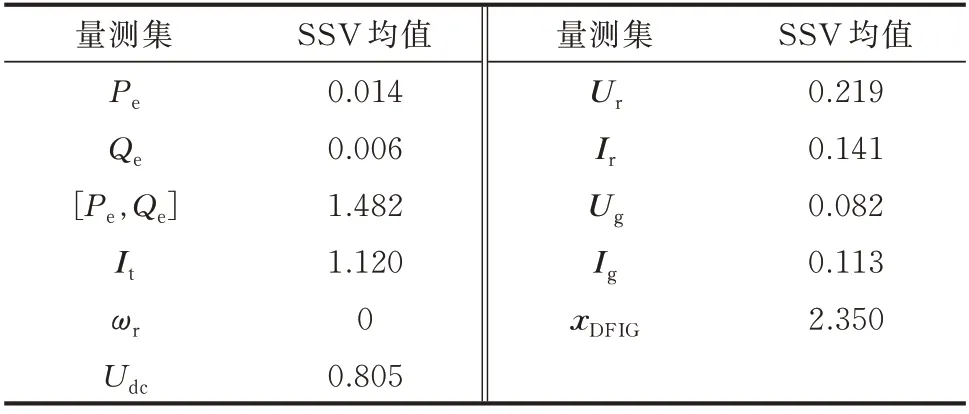
表1 各量测集对应的SSV 均值Table 1 Mean value of SSV corresponding to each measurement set

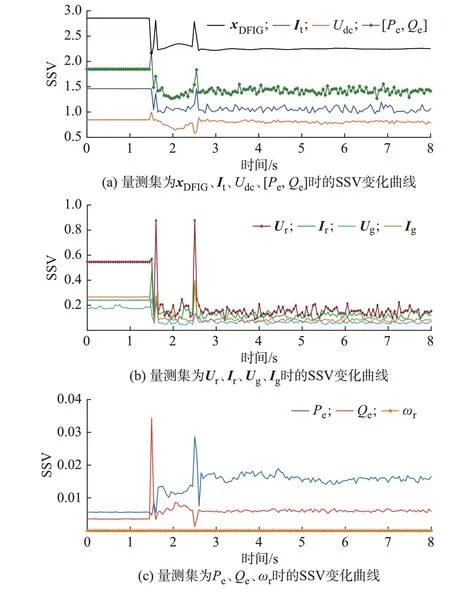
图2 各量测集的SSV 变化曲线Fig.2 Variation curves of SSV with each measurement set

从表1 以及图2 可以看出,当双馈风机输出的有功功率Pe和无功功率Qe单独作为量测时,其可观性矩阵的SSV 较小；Pe和Qe同时作为量测时的SSV 与理想情况（即所有状态变量都可直接量测）较接近,即该量测集可为双馈风机的状态估计提供较好的可观性；双馈风机输出电流It、直流电容电压Udc对应的SSV 也较大,说明将其作为量测也可提供较高的状态可观性；将ωr作为量测时,可观性矩阵的最小奇异值为零,说明此时系统是不可观的；其他量测集的SSV 较小,说明能够提供的状态信息较少。

在SSV 较大的量测集中,首先考虑到［Pe,Qe］的计算需要用到It,即该量测集提供的信息中已经包含It的信息,故选择［Pe,Qe］以及Udc作为量测；其次,由于滤波电感的动态变化快,仅靠以上量测无法及时跟踪其状态变化,故将Ig也作为量测之一。综上,选定的量测集yfinal如下:

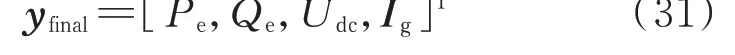
量测集yfinal的可观性矩阵SSV 的变化如图3 所示。由图3 可知,其SSV 比［Pe,Qe］更接近所有状态可直接量测时的SSV,说明其可提供更多状态信息。在附录B 图B1 中给出了部分其他量测组合的讨论,以证明所选量测集yfinal的合理性。

图3 选定的量测集对应SSV 的变化曲线Fig.3 Variation curves of SSV corresponding to selected measurement sets

4.2 不同量测集状态估计结果的比较

可观性分析的最终目的是为了选择合适的量测集以提高动态状态估计的收敛速度与精度,故本节将利用CKF 对双馈风机进行状态估计以验证上述量测选择是否恰当。本节选择Pe、［Pe,Qe］、［Pe,Qe,Udc］以及yfinal分别作为量测,对比CKF 的状态估计结果,如图4 和图5 所示。由于控制器中间变量x1～x7无实际物理意义,其估计结果未给出。

由图4 可知,所有量测集下ψds、ψqs的估计结果都收敛且较准确,说明Pe和Qe能够提供这2 个状态的信息,但由图5（a）和（b）可知,Pe和［Pe,Qe］的估计结果在扰动后经过一段时间才收敛到真实值,其他量测则较快收敛；Pe和［Pe,Qe］作为量测时部分状态量的估计结果不收敛,其中,ωr、Udc的估计结果［Pe,Qe］好于Pe；［Pe,Qe,Udc］和yfinal作为量测时所有状态的估计结果都能收敛,但是扰动发生后一段时间内［Pe,Qe,Udc］的估计结果偏离真实值,且经过较长时间才收敛到实际值,收敛速度较慢；而yfinal增加滤波电感电流作为量测后,其估计结果在扰动后能够较快地收敛到真实值,说明滤波电感的时间常数较小,动态变化较快,将Ig作为量测是必要的。然而,在扰动期间yfinal的估计结果仍存在一定的误差,如图5（c）和（d）中ωr和ψqr的放大图所示。

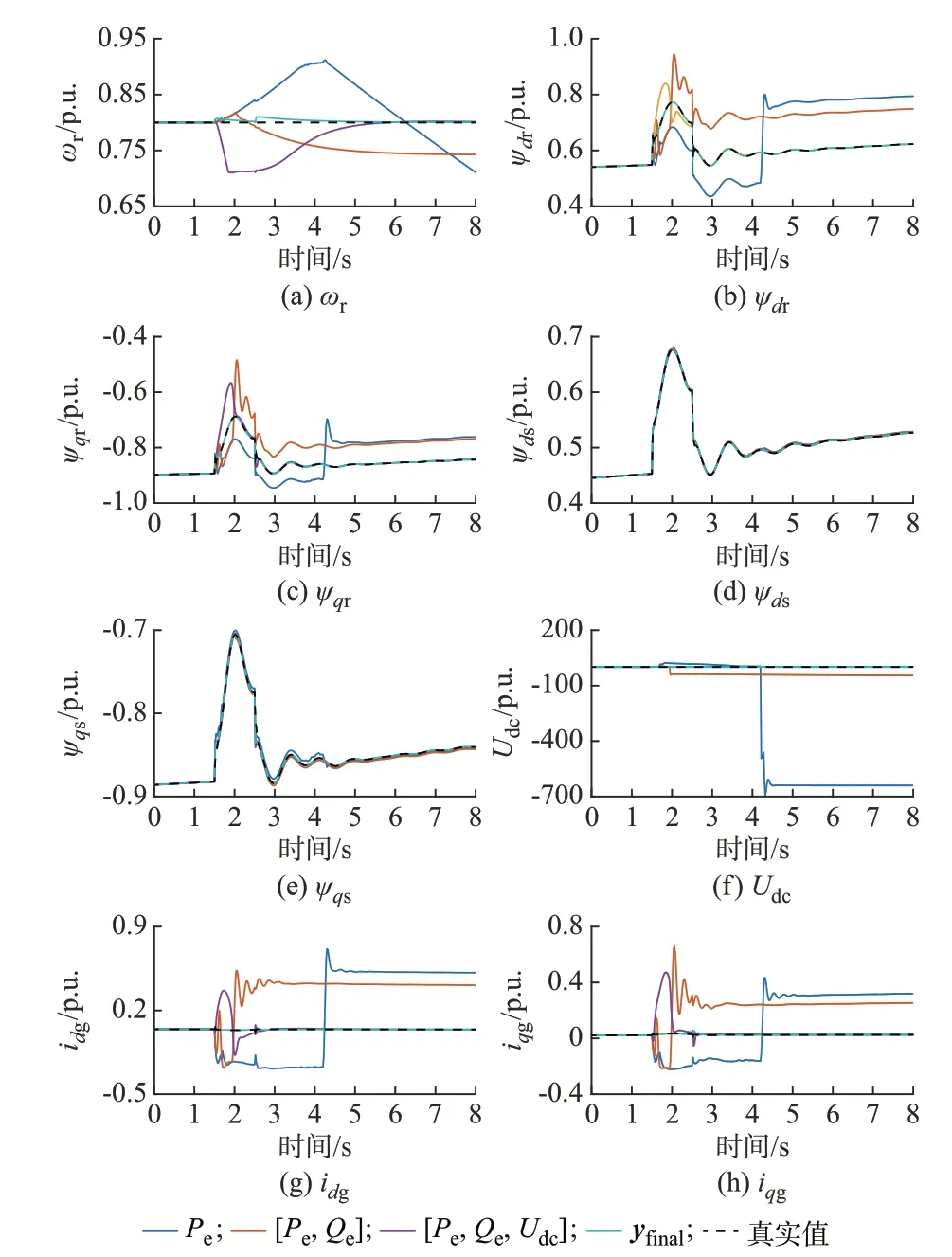
图4 不同量测集的状态估计结果Fig.4 State estimation results of different measurement sets

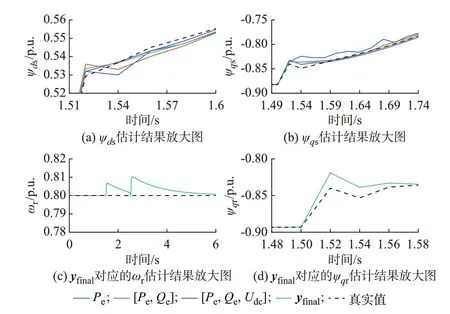
图5 状态估计结果的放大图Fig.5 Enlarged view of state estimation results

4.3 多步预报CKF 算法测试

量测集的正确选取是实现准确DSE 的基础,但由于量测速率不足、量测噪声等原因,DSE 结果仍会存在一定偏差,所以在通过可观性分析确定量测集后,可通过对比L固定取值与自适应取值的状态估计结果来测试所提多步预报CKF 方法的有效性。设置L分别等于1、10、30、60、100,其中L=1 即为普通CKF。为量化评估L取不同值时状态向量预报值和状态估计值的准确程度,采用均方根误差（rootmean-squared error,RMSE）作为整体误差评价指标,并用σk表示第k个离散时间的均方根误差,具体定义如下:

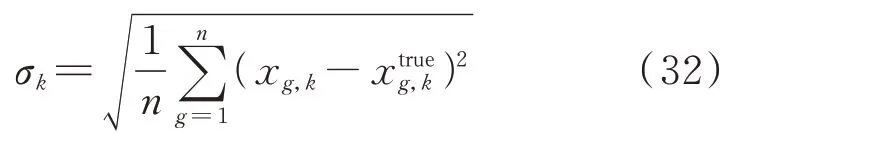
式中:xg,k为第k个离散时间的状态预报向量或状态估计向量的第g个变量；xtrueg,k为第k个离散时间的状态向量第g个变量的真实值。

不同L状态预报向量的均方根误差和自适应L取值的变化如图6 所示。由图6（a）可知,无论是在稳态还是故障期间,L=1 的均方根误差都是最大的,即预报最不准确；随着L的增大,预报值的均方根误差减小,说明增大L可以提高预报值的准确性；但L等于30、60 和100 时的均方根误差差别很小,说明L增大到一定程度时,继续增大L所带来的精度提升有限。此外,扰动发生（1.5 s 和2.5 s）时的均方根误差会显著增大,这是因为状态预报需要用到前一时刻的状态和输入,同时扰动不可预测,导致预报值误差增大。图6（b）给出了自适应L取值的变化。从图中可以看到,在扰动时刻L迅速增大,且在扰动期间因预报误差增加而保持较大值,其他时间维持较低值,整个过程中大部分取值小于20,与上述均方根误差分析结果保持一致。

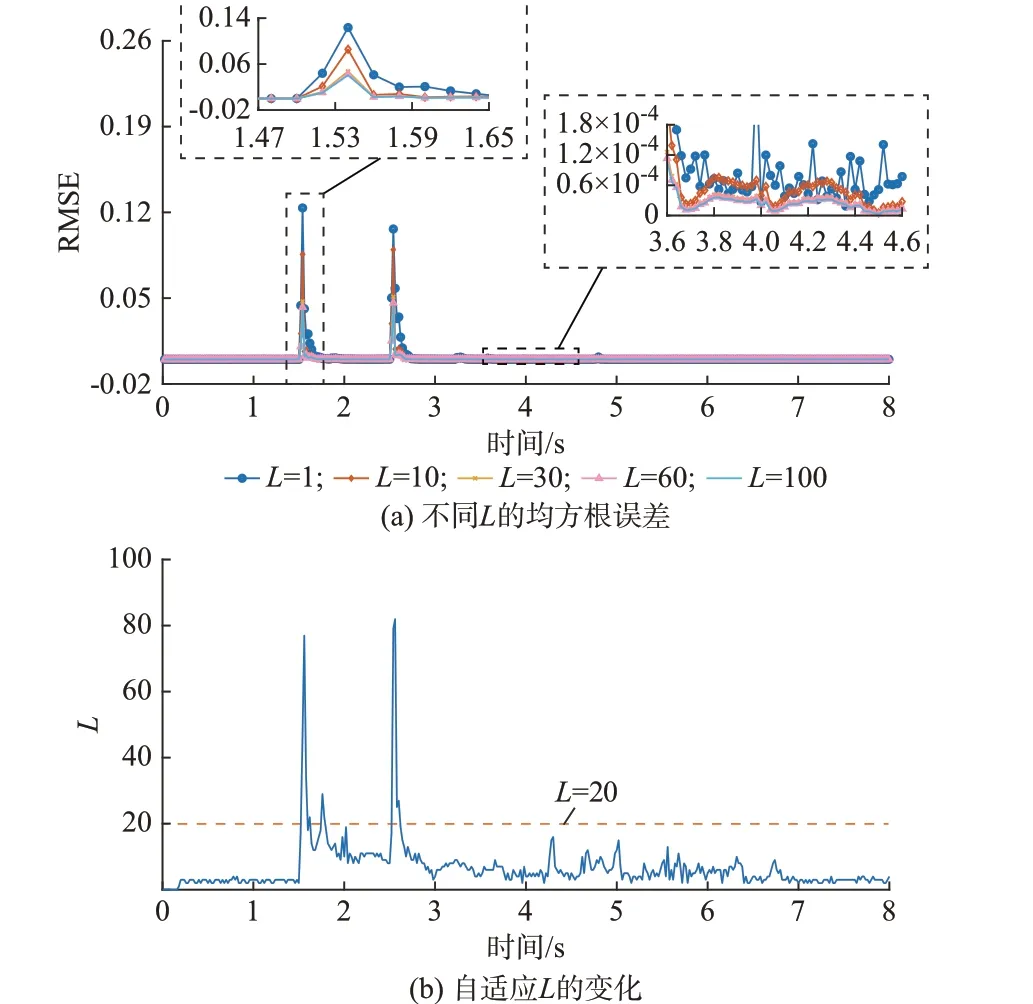
图6 不同L 的均方根误差和自适应LFig.6 RMSE of different L and adaptive L

L取不同值时多步预报CKF 的状态估计结果见附录B 图B2,图7 给出了ωr和ψqr的估计结果,可知,在合理选择量测集的基础上,CKF 基本能够跟踪状态变化的轨迹,但在扰动发生时会产生一定的偏差。由图7 可知,在一定范围内增大L可以减小这一误差,从而降低扰动对状态估计结果的影响,证明了所提多步预报CKF 方法的有效性。

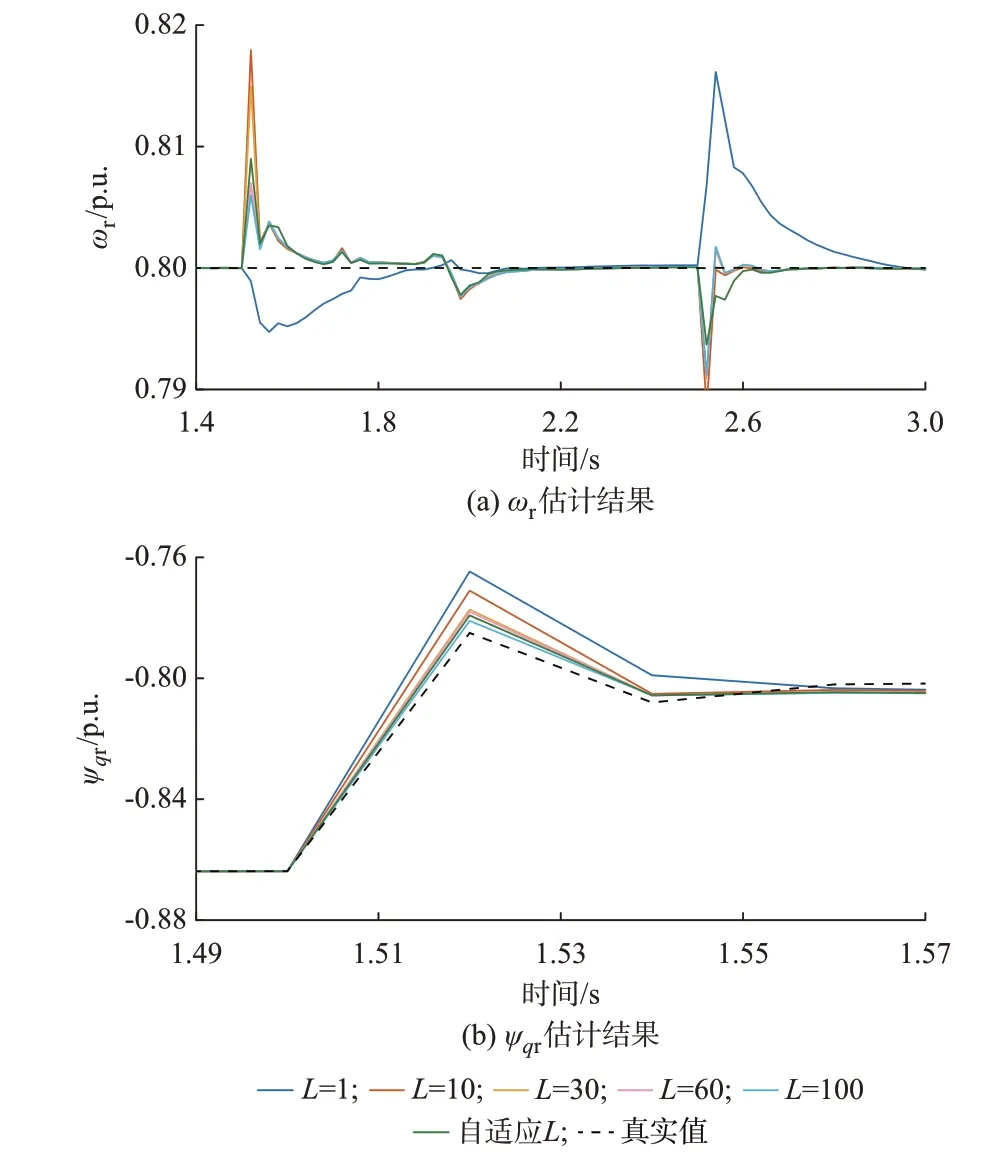
图7 不同L 的ωr 和ψdr 估计结果Fig.7 Estimation results of ωr and ψdr with different L

L取不同值时多步预报CKF 方法状态估计结果的均方根误差与计算时间如表2 所示。

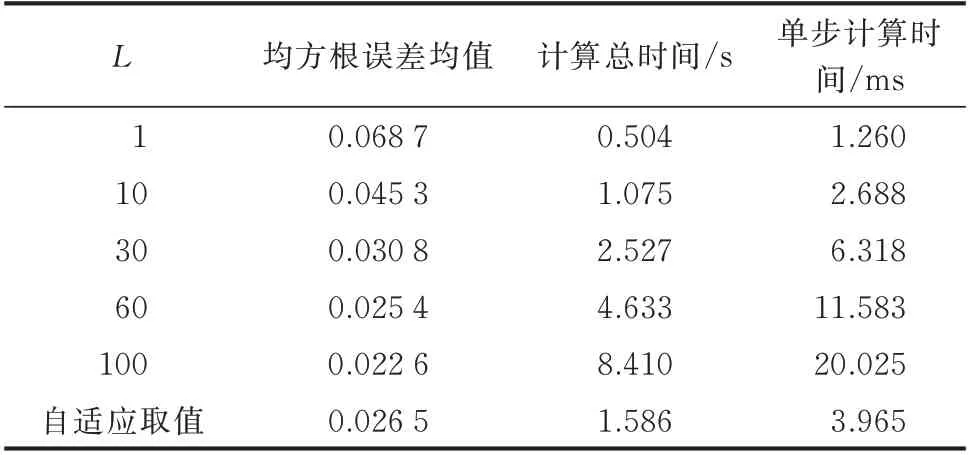
表2 不同L 的多步预报CKF 方法均方根误差与计算时间Table 2 RMSE and computation time of multi-step prediction CKF with different L

由表2 可知,增大L时均方根误差会减小,但随着L的增加均方根误差的减少幅度也变小,同时计算时间却会快速增加,说明L需要在一定范围内取值以平衡精度和计算时间的要求。所提L自适应取值方法的均方根误差与L等于30、60 时基本一致,但计算速度更快,更重要的是,其可自适应取值,通用性较强。

5 结语

可观性分析对于双馈风机动态状态估计量测集的选择有重要指导意义。本文推导了Lie 导数计算可观性矩阵的原理,基于AD 和ADOL-C 工具实现了不同量测集下双馈风机可观性矩阵的快速计算,并利用奇异值分解和最小奇异值对不同量测集的可观性进行了定量评价,选出了最佳量测集；然后,提出多步预报CKF 方法,缓解了双馈风机部分状态变量变化较快导致预报不准确的问题,并且能够基于预报误差自适应确定参数L；最后,基于改进IEEE 39 节点系统对双馈风机进行了可观性分析,选出使双馈风机状态具有较高可观性的量测集,在此基础上验证了所提多步预报CKF 方法的有效性。

本文不足之处在于假设双馈风机模型和参数已知且量测准确,但实际中双馈风机模型和参数可能未正确校对,量测数据也可能存在不良数据。因此,下一步将考虑采用鲁棒滤波方法来应对模型、参数和量测中的不确定性误差。

附录见本刊网络版（http：//www.aeps-info.com/aeps/ch/index.aspx），扫英文摘要后二维码可以阅读网络全文。