考虑不变桨风速范围的风电机组有功功率控制
2023-02-27陈载宇殷明慧
顾 伟,陈载宇,殷明慧,李 群,李 强,邹 云
(1. 南京理工大学自动化学院,江苏省南京市 210094;2. 国网江苏省电力有限公司电力科学研究院,江苏省南京市 211103)
0 引言
风电大规模、高渗透率接入电网将逐步形成新能源为主体的新型电力系统[1-2]。在此背景下,迫切需要变速-变桨风电机组从常规采用的最大功率点跟踪(maximum power point tracking,MPPT)控制转变为跟踪电网功率指令的有功功率控制(active power control,APC)[3-4],以参与电网的自动发电控制,支撑系统的有功功率平衡。
现有APC 方法主要有基于闭环转速控制[3,5-7]和基于预设功率给定[8-12]两种实现方式,文献[13]分别将两者定义为风轮主动变速和被动变速方法。主动变速方法在闭环反馈控制框架下令风电机组跟踪设定稳定平衡点,从而快速运行至平衡点处以响应功率指令;被动变速方法可以利用大惯量风轮惯性响应来应对风速波动,具有功率指令响应精确、传动链载荷小和变桨动作量少等特点,更适用于湍流风速场景[13],因此也是本文的研究对象。
对于被动变速APC 方法,现有研究的关注点之一是如何利用风轮被动变速缓冲风速波动,以减轻变桨机构动作疲劳。转速调节(rotor speed control,RSC)方法[8]最早提出了优先利用风轮惯性响应平抑因风速波动带来的风电机组气动(输入)功率与电磁(输出)功率的不平衡。但因仅利用了零度桨距角风轮的被动变速,RSC 方法会在风速升高或电网功率指令降低时退化为只依赖变桨调节的恒转速控制。为此,文献[9]提出了集成变速-变桨APC(下文简称IAPC),通过利用任意桨距角风轮被动变速应对风速波动,有效减少了变桨动作。类似地,文献[14]提出的分段桨距控制也具有利用任意桨距角风轮被动变速的效果。
总结现有被动变速APC 方法,桨距角调节均发生在风轮转速达到转速边界时,均为限转速控制。这使得桨距角设定与风速、风电机组动态和反馈控制器有关,具有很强的随机性和不确定性。可见,现有研究中的桨距角设定只关注限转速调节,忽视了其对风轮被动变速缓冲风速波动的影响。然而,本文发现桨距角会明显改变被动变速风轮的动态特性,体现在不同桨距角风轮通过被动变速能够独立应对的风速波动范围(即不变桨风速范围[15])存在明显差异。因此,随机设定的桨距角势必会影响风轮被动变速对风速波动的缓冲效果,即风电机组更容易达到转速边界而出现风轮超速或电磁功率跌落,削弱了APC 的控制性能。
为此,本文基于桨距角对不变桨风速范围的影响进行分析,以保证风电机组的稳定和尽可能利用风轮被动变速缓冲风速波动为原则,讨论了桨距角与风速变化范围之间的适配关系。在此基础上,提出了考虑不变桨风速范围的风电机组APC 方法。该方法通过增加适配桨距角的设定环节,使得被动变速风轮的不变桨风速范围动态匹配风速波动范围,降低了风轮达到转速边界的频次,进而缓解了风轮超速和电磁功率跌落。最后,基于风电机组动模实验平台,实验验证了本文方法的有效性。
1 风电机组模型与APC
本章主要介绍变速-变桨风电机组的数学模型、APC 的基本原理以及基于被动变速运行模式的风电机组APC。
1.1 风电机组数学模型
完整的变速-变桨永磁同步风力发电系统包括风轮、传动链、发电机与变流器等部分,如附录A 图A1 所示。考虑到电磁动态的响应速度要远快于机械动态的响应速度[16],本文主要关注机械动态,忽略电磁动态过程,认为现有电机控制可以快速且精准地响应电磁转矩参考值。
由水平轴风电机组的气动理论可知,风轮捕获的气动功率Pm为:

式中:ρ为空气密度;R为风轮半径;v为风速;CP为风能利用系数,是叶尖速比λ与桨距角β的函数,当桨距角为零时,CP在最佳叶尖速比λopt处取得最大值CP,max;ω为风轮转速。
风电机组的机电动态是指含风轮、齿轮箱和发电机转子的传动轴转速变化过程。若齿轮箱变速比为ng,机电动态可表示为如式(3)所示的双质量块模型[16]。

式中:Jr和Jg分别为风轮与发电机转子的转动惯量;ωg为发电机转速;Tls和Ths分别为低速侧和高速侧转矩;Dr和Dg分别为风轮与发电机的外阻尼系数;Tm和Tg分别为气动转矩与电磁转矩。
将低速轴假定为理想的刚性轴,则风电机组机电动态可简化为如式(4)所示的单质量块集总模型[17]。

1.2 基于被动变速的APC
在风电机组最大出力、最高转速等约束条件[18]下,风电场控制将电网有功功率需求分配给场内的风电机组。风电机组APC 的控制目标是让风电机组按功率指令Pcmd输出电磁功率,同时维持风电机组机电动态稳定。在稳态视角下,风电机组在风速v下存在稳定平衡点(ω0,β0)(ω0和β0分别为稳定平衡点处的风轮转速和桨距角),使得捕获气动功率、输出电磁功率与电网功率指令三者相等,即
那么风电机组运行在该稳定平衡点,便实现了APC的控制目标。基于被动变速的IAPC 见图1,一般包括3 个环节:变速区间内的风轮被动变速、限转速的变桨调节和低转速段的风电机组稳定。

图1 基于被动变速的IAPCFig.1 IAPC based on passive speed variation
1)变速区间内的风轮被动变速。当风轮转速ω处于变速区间[ωopt,ωN]内时,风电机组桨距角保持不变,电磁功率直接响应电网功率指令,发送至变流器的电磁转矩指令Tg,ref按式(6)给定。
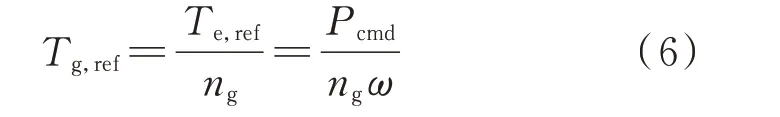
式中:Te,ref为等效在低速侧的电磁转矩指令。
此时,风轮转速不依靠电磁功率主动调节,而随传动链承受不平衡功率(即Pm-Pe)自由变化。被动变速能够自然利用风轮动能缓冲风电机组输入/输出功率的短时不平衡,无须时刻调节电磁功率或桨距角。
2)限转速的变桨调节。当风轮转速超出变速区间,即ω>ωN或ω<ωopt时,通过桨距角调节将风轮转速限制在变速区间内。具体如图1 所示,分别在转速上边界ωN上调桨距角和转速下边界ωopt下调桨距角,并通常根据实际转速相对于转速边界的偏差,经由比例-积分(PI)环节确定桨距角指令[8-9,19]。
3)低转速段的风电机组稳定。为避免低风速下风电机组失稳,当风速降低使风轮转速下降至ωopt时,风电机组运行切换至MPPT 模式,电磁转矩指令按式(7)给定。
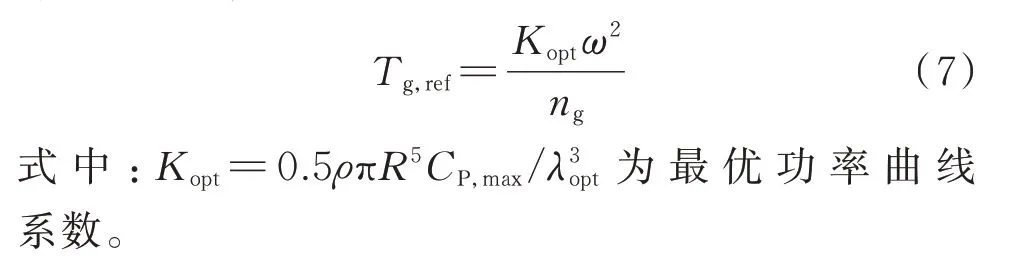
值得注意的是,虽然是有限转速的变桨调节,但由于风轮的大惯量和变桨机构的动作延迟,风电机组在达到变速区间边界时均容易出现不同程度的转速超调,即ω>ωN或ω<ωopt。由式(7)可知,后者会造成电磁功率跌落。
由上述分析可知,现有被动变速APC 中的桨距角调节大都在风轮转速达到边界时启动,并基于转速反馈控制律实现。桨距角设定与风速、风电机组机电动态和控制器密切相关,具有很强的随机性和不确定性。这种只关注限转速控制的变桨调节未考虑到桨距角对风轮被动变速缓冲风速波动效果的影响,忽视了针对风轮被动变速过程的桨距角优化设定。
2 被动变速风轮桨距角与风速波动范围的适配分析
针对上述问题,本章首先分析风电机组不变桨风速范围的变化规律,其次通过讨论实际风速波动范围与不变桨风速范围之间的关系,确定与风速波动范围相匹配的桨距角。
2.1 不变桨风速范围及其随桨距角的变化分析
风电机组被动变速利用风轮动能缓冲输入/输出功率之间的不平衡。其中,桨距角是影响气动功率的主要因素,不同桨距角下的风轮被动变速特性存在差异。基于不变桨风速范围[15],本节首先分析桨距角对风轮被动变速的影响。
不变桨风速范围表征了APC 方法利用风轮变速减少变桨动作的效果。对于功率指令为Pcmd和变速区间设为[ωL,ωU]的APC 方法,当桨距角为β时,存在一个最大的风速波动范围Unpv,即



可见,只要风速波动不超出Unpv(β),其可由桨距角为β的风轮在变速区间[ωL,ωU]内被动变速完全应对,无须启动桨距角调节,否则,若风速超出Unpv(β)(v>vU(β)或v 由式(9)和式(10)可以看出,Unpv与风电机组参数(R、CP、ωN)、环境参数(ρ)和功率指令相关,但是风电机组参数和环境参数不可调,Unpv主要受功率指令影响。以额定容量为1.5 MW 的风电机组[20]为例,当应用IAPC 方法且功率指令设定为300 kW时,不同桨距角下Unpv的上边界vU和下边界vL分别如附录B 图B2 中虚线和实线所示。在每一个桨距角下,vU和vL共同确定了风电机组在该桨距角下仅利用风轮被动变速(而不启动变桨调节)可应对的风速变化范围。可以发现,桨距角变化对Unpv的影响主要体现在风速水平和波动范围两个方面。 1)Unpv内的风速水平随桨距角的增大呈现升高趋势。当桨距角增大时,风轮捕获气动功率的能力下降(即桨距角对应的CP-λ曲线整体下移)。为实现给定的功率指令目标,风电机组则需要在更高的风速下捕获足够的气动功率。这意味着桨距角越大,被动变速风轮可以应对幅值越高的风速波动。 2)Unpv随桨距角增大呈现扩大趋势。当桨距角增大时,风轮捕获气动功率对转速变化的敏感度升高,使得相同风速扰动下的风轮转速变化量减小。因此,桨距角越大,相同变速区间的风轮被动变速可以缓冲更大范围的风速波动。 3)功率指令越高,相同桨距角下的Unpv上边界和下边界均增大,则Unpv内的风速幅值越大。同时,由于功率指令增大使得风电机组变速区间缩小,使得Unpv也有所缩小。 综上,桨距角会显著影响被动变速风轮的动态特性,主要体现在不同桨距角对应的不变桨风速范围存在明显差异。因此,面对实际湍流风速的波动范围变化(即平均风速和湍流强度变化),有必要设定合适的桨距角,从而利用该桨距角风轮的被动变速来更有效地缓冲风速波动。 在风电机组运行过程中,风速波动范围随机变化,且未必处于当前桨距角对应的不变桨风速范围内。两者之间的关系直接影响到APC 的控制性能。附录B 图B3 所示为一段由Bladed 软件[21]生成的湍流风速序列,可以看出风速特征在分钟级时间尺度上就会存在明显的差异[22]。 风电机组在某一桨距角下的Unpv是有限的,很难全面覆盖长时段湍流风速波动范围。但将时间尺度缩短到分钟级,风速波动范围Uv=[vmin,vmax]与Unpv存在可比性。为使风轮被动变速更有效地缓冲湍流风速,缓解风电机组超速和电磁功率跌落,有必要比较分析Unpv与Uv之间的关系,为合理设定匹配分钟级风速波动的桨距角奠定基础。 图2 所示为波动范围相同、幅值水平不同的Uv,并将其与Unpv(β)比较。由图可知,随着桨距角设置的不同,Unpv(β)与Uv之间至少存在6 种关系。 图2 Uv 与U np v 之间的6 种关系Fig.2 Six kinds of relationship between Uv and U np v 进一步地,为了阐述每种关系意味着的被动变速风轮的动态过程及其达到变速区间边界(ωU或ωL)的情况,在风轮转速-风速平面上,对应固定β(即β1至β6)的风电机组稳定平衡点的集合(黑色实线所示)见附录B 图B4(a)至(f)。根据图B4 可知,变速区间[ωL,ωU]确定的风速范围即为Unpv(β)。共用风速纵轴的风速序列确定了Uv,其中的最高风速vmax(或最低风速vmin)对应的风轮转速若落在变速区间内,则是可行稳定平衡点,否则,便是不可行稳定平衡点,且意味着风电机组有可能运行至变速区间边界而启动变桨调节。通过比较Unpv(β)与Uv,它们的6 种关系描述如下: 1)关系1:Unpv(β1)∩Uv=∅,且vU(β1) 2)关 系 2:vmin 3)关 系 3:Unpv(β3)∩Uv=[vmin,vU(β3)],即vL(β3) 4)关 系4:Unpv(β4)∩Uv=[vL(β4),vmax],即vmin 5)关 系 5:vL(β5) 6)关系6:Unpv(β6)∩Uv=∅,且vmax 由上述不变桨风速范围与风速变化范围之间关系的讨论可知,桨距角会明显改变被动变速风轮触及转速边界的情况,进而影响到风电机组APC 的控制性能。两类范围的关系讨论为适配湍流风速的桨距角确定奠定了基础。 基于2.2 节Unpv(β)与Uv的关系分析,本文以充分利用风轮被动变速,尽量避免风电机组超出变速区间为目标,得到与风速波动相适配的桨距角选取原则如下: 1)首先,应满足关系5(Uv⊆Unpv(β)),这样仅利用风轮被动变速便可缓冲风速波动,而无须启动转速边界处的变桨动作。 2)若不存在满足关系5 的桨距角,则应让Unpv(β)与Uv的交集最大,且风轮转速不触及ωL。前者可以最大程度地利用被动变速,而减少风电机组达到转速边界的频次;后者是为了避免风电机组因电磁功率跌落而不能实现APC 的控制功能。 综合上述原则,对于给定Uv,本节利用Unpv(β)与Uv的关系描述,给出适配桨距角β̂确定策略: 依据第2 章适配桨距角的确定原则,本章提出考虑Unpv的风电机组APC 方法。该方法通过主动设定适配桨距角β̂,使得被动变速风轮的Unpv动态匹配湍流风速的实际变化范围,进而提升APC 性能。 改进APC 方法的控制原理框图如图3 所示,在IAPC 方法[9]的基础上增加了基于β̂搜索的桨距角设定环节。除了原有的变速区间内风轮被动变速、限转速的变桨调节和低转速段风电机组稳定3 个环节之外,新增了基于β̂搜索的桨距角设定环节。该桨距角设定环节具体如下。 图3 所提APC 方法的原理图Fig.3 Principle diagram of proposed APC method 1)Uv估计模块。 应用基于长短期记忆(LSTM)网络模型的风速预测方法[24-25](参数设定见附录C 表C1),预测得到下一周期的平均风速vˉfc,并结合风场的湍流等级特征估计风速变化范围Uv。基于该风速预测方法,本文对分钟级时间尺度平均风速预测进行仿真。仿真结果表明,预测精度较高,预测误差在10%以内(如附录C 图C1 所示)。鉴于分钟级的Uv与Unpv具有可比性,并对比不同周期设定时的风电机组APC 的控制性能,本文方法将Uv的周期经验性地设定为1 min。 2)β̂搜 索 模 块。根 据Uv估 计 值,并 基 于2.3 节所述原则和策略,搜索紧邻下一周期的适配桨距角β̂。由于是有限范围内的单变量寻优,本文在桨距角运行范围[βmin,βmax]内采用遍历方法,搜索满足式(11)的β̂,遍历搜索步长为0.1°。特别地,如果存在多个满足式(11)的桨距角,则选择与当前桨距角偏差最小的值作为β̂。 需要注意的是,虽然通过估计风速范围寻优得到的适配桨距角与实际风速对应的适配桨距角会存在偏差,但是由于大惯量风轮具有慢动态特性,可以应对短时的风速大幅变化,对APC 的控制性能影响较小。 改进方法对于Uv估计、β̂搜索和设定是周期性的,即在每个周期开始前,根据预测得到的平均风速和风场内湍流等级特征信息,估计出这一周期的Uv,并据此搜索这一周期的β̂,进而将桨距角设定为该β̂。需要注意的是,尽管主动设定了适配桨距角,但风电机组依然存在达到变速区间边界的可能。如果发生,则基于PI 的变桨调节会启动,将风轮转速限制在变速区间内。 综上,由于保留了变速区间内的风轮被动变速和限转速的变桨调节两个环节,本文方法继承了IAPC 方法的改进机理:分别利用被动变速和PI 变桨调节应对湍流风速中的高频率、小幅值和低频率、大幅值的波动分量。在此基础上,新增的桨距角设定环节不仅克服了被动变速风轮桨距角设定的随机性和不确定性,而且Unpv(β̂)与Uv的适配性使得大惯量风轮能更好地缓冲高频率、小幅值的风速波动分量,减小因触及转速边界而引发的风轮超速或电磁功率跌落。 本章应用风电机组动模实验平台,实验验证本文提出方法的有效性。首先,介绍风电机组动模实验平台;其次,介绍APC 性能的评价指标;最后,针对实验结果进行比较分析。 风 电 机 组 动 模 实 验 平 台[26]如 附 录D 图D1 所示,包括风轮模拟器、发电变流部分和APC 控制器。该实验平台能够模拟美国国家可再生能源实验室CART 3 风电机组[27](参数见附录D 表D1)的气动特性和机械动态。 1)风轮模拟器由驱动变流器、18.5 kW 三相异步电机、机械飞轮和可编程逻辑控制器(PLC)组成。通过应用功率比例缩放、气动-弹性耦合仿真、惯量补偿和阻尼补偿算法,该实验平台可基于小容量、低转动惯量机组模拟大容量、大转动惯量风轮的气动特性和慢动态特性[26,28-30]。此外,对变桨执行机构的动作特性是通过一阶惯性环节和变桨速率限制来模拟的。 2)发电变流部分与实际风电机组基本相同,包括15 kW 永磁同步发电机和并网变流器(含机侧变流器和网侧变流器)。机侧变流器接收来自APC 控制器的电磁转矩指令Tg,ref,控制发电机的电磁转矩Tg。由于采用了功率缩放技术(缩放系数为50),模拟风电机组的输出功率是实验电机输出电磁功率的50 倍。 3)APC 控制器。在PLC 中编程实现APC 控制策略,包括RSC 方法、IAPC 方法和本文方法。控制器在每一个控制周期计算电磁转矩指令Tg,ref和桨距角指令βref,并分别发送至机侧变流器和风轮模拟程序。 本节从风轮转速调节性能、变桨机构疲劳载荷和功率指令响应性能3 个方面比较分析不同APC方法,具体指标介绍如下。 1)为了评价风轮转速性能,选取风轮超速(即转速大于ωN)累积时间tU和最大转速偏差率ηmaxU来描述风轮超速的严重程度。其中,ωmaxU为统计时段内的风轮最大转速。类似地,根据实验数据统计得到转速低于ωL的累积时间tL,用于描述风轮转速越过ωL而导致电磁功率跌落的严重程度。 2)选取变桨动作量Δβsum[5,9]来反映变桨执行机构疲劳载荷。其中,β(i)为第i个采样时刻的桨距角,N为统计时段内采样次数。 3)考虑到APC 的控制目标,选取电磁功率相对电网功率指令的偏差统计σPe指标[31]来综合反映风电机组能否快速、准确地跟踪功率指令。其中,Pe(i)为第i个采样时刻的输出电磁功率。需要指出的是,电磁功率跌落仅因风轮持续减速越过ωL而导致,因此tL与σPe具有正相关性。 在600 s 湍流风速(平均风速10 m/s,湍流强度C 级)下,针对不同功率指令情况进行实验验证。图4 所示为功率指令为150 kW 时风电机组在RSC 方法、IAPC 方法和本文方法下的转速、桨距角和电磁功率轨迹,表1 所示为相应控制性能评价指标。其他功率指令下的风电机组转速、桨距角和电磁功率轨迹如附录D 所示。 图4 不同APC 方法的比较Fig.4 Comparison of different APC methods 表1 控制性能评价指标Table 1 Evaluation indices of control performance 1)风轮转速调节性能 考虑到风轮转速调节性能的改善是其他APC控制性能提升的根本原因,本文首先针对该类性能指标,比较分析3 种APC 方法。 对于RSC 方法,因为仅运用了零度桨距角风轮被动变速,风速增大使得风轮很容易加速到ωN,进而频繁触发ωN处的限转速变桨调节。相应地,转速轨迹表现为持续在ωN附近波动,并反复出现风轮超速,tU高达204.92 s。而且,由于变桨机构动作缓慢,且电磁功率因响应电网指令而无法参与限转速调节,风轮超速明显(ηmaxU=11.20%)。此外,同样因为零度桨距角有助于获得强劲的气动功率,零度桨距角风轮不易减速到ωopt,tL为0。 由于IAPC 方法应用了任意(零度和非零度)桨距角风轮被动变速,转速不再是RSC 方法下的在ωN附近持续波动,而是在变速区间[ωopt,ωN]大范围变化,tU大幅减小到76.88 s。但是,限转速变桨调节只关注转速控制效果,通过其设定的桨距角不仅不考虑后续风轮被动变速对风速波动的缓冲效果,而且具有很强的随机性和不确定性。例如,观察图4 风轮转速和桨距角实验曲线可以看出,t=7 min 内风轮转速低于ωopt与相邻前次ωN处限转速变桨调节(紫色虚线圆框所示)引发的桨距角上调幅度过大有关。相较于RSC 方法,IAPC 方法即便更充分利用了风轮被动变速,但随机且与实际风速无关的桨距角设定依然会使风电机组容易触及转速边界,tU与tL之和达到了120.44 s。 对于本文方法,由于在IAPC 方法的基础上增加了考虑Unpv的桨距角设定环节,根据风速信息动态更新的适配桨距角提升了风轮被动变速对湍流风速的缓冲效果,进而有效降低了风轮达到转速边界的频次(tU和tL大幅降低至20.64 s 和0 s),缓解了风电机组超速(ηmaxU=4.36%)并避免了电磁功率跌落。 2)变桨动作量 因为限转速变桨调节是引发变桨机构动作的主要原因,所以风轮转速调节性能(即风轮被动变速对湍流风速的缓冲效果)越好,则风电机组越少触及转速边界(tU和tL越小),进而Δβsum越低。由表1 可见,在功率指令为150 kW(0.25 p.u.)时,仅利用零度桨距角风轮被动变速的RSC 方法,Δβsum高达173.71°;IAPC 方法应用了非零度桨距角风轮被动变速,但桨距角设定未适配风速变化范围,Δβsum缓解为89.10°;在此基础上,本文方法增加适配桨距角的设定环节,使得被动变速风轮能更好地缓冲高频率、小幅值的风速波动分量,Δβsum相应降低到42.24°,其中还包括了主动设定适配桨距角导致的25.42°。 3)功率指令响应性能 当风电机组在ωopt处出现转速超调(即ω<ωopt)时,为维持风电机组转速稳定,风电机组运行切换到MPPT 模式,导致电磁功率出现跌落。风轮转速低于ωopt的情况是影响风电机组输出电磁功率对功率指令响应性能的主要因素。tL越大,则功率指令响应性能越差,σPe越大。由表1 可见,相较于IAPC 方法,由于确定适配桨距角遵循了风轮转速不触及ωopt的原则,本文方法将σPe降低为0,改善了功率指令响应性能。 虽然本文方法需要估计风速波动范围和遍历搜索适配桨距角,但由于风速波动范围估计耗时较少,且适配桨距角的确定是有限范围内的单变量寻优,计算负担不重。经测试,单次适配桨距角确定所需平均时间为18.8 ms,而且风电机组变桨执行机构变桨速率较快,为5~10(°)/s[32]。可见,本文方法完全满足适配桨距角的更新、设定周期(分钟级),不会影响APC 的工程应用和性能。 当功率指令为180 kW(0.3 p.u.)时,相较于RSC 和IAPC 方法,本文方法在风轮转速调节性能、变桨动作量方面的控制性能都有较为明显的改善,见附录D 图D2 和表D2。与功率指令为150 kW 的场景相似,此处不再赘述APC 的控制性能提升的具体原因。由于t=7 min 内的风速幅值较低且持续时间较长,3 种APC 方法下的风电机组运行均切换到MPPT 模式,通过降低电磁功率避免风电机组持续减速,以此保证风电机组转速稳定。 进一步地,在附录D 图D3 所示的风速波动下,本文方法通过设定与风速波动范围相适配的风轮桨距角,可以完全利用转速区间内的风轮被动变速来应对风速波动,风轮转速未达到转速边界而产生边界处的恒转速变桨。而RSC 和IAPC 方法下风轮转速则多次触发转速边界,导致风轮转速超速和电磁功率跌落。 对于被动变速APC,变速区间内风轮变速对于湍流风速的缓冲效果成为提升控制性能的关键所在。虽然现有APC 方法在变桨控制环节采用先进控制算法,实现了对风轮转速超速的抑制,但是其仅关注限转速控制效果,忽视了桨距角优化设定对风轮被动变速过程的影响。这使得桨距角运行值具有很强的随机性,并导致风轮容易触及转速边界而引发风轮超速和电磁功率跌落问题。为此,本文分析了不变桨风速范围随桨距角的变化关系,建立了桨距角与风速变化范围之间的适配关系。在此基础上,本文提出了考虑不变桨风速范围的APC 方法。该方法通过动态设定与风速波动范围相适配的桨距角,降低了风轮达到转速边界的频次,提升了风电机组APC 在风轮转速调节、变桨机构疲劳载荷和功率指令响应3 个方面的性能。 需要指出的是,对于本文方法,当风轮转速达到变速区间边界时,同样可以采样先进控制算法来进一步改善风轮转速超速程度。 本文在撰写过程中获得国家自然科学基金项目(61773214)资助,特此感谢! 附录见本刊网络版(http://www.aeps-info.com/aeps/ch/index.aspx),扫英文摘要后二维码可以阅读网络全文。2.2 Unp v 与风速变化范围的关系分析
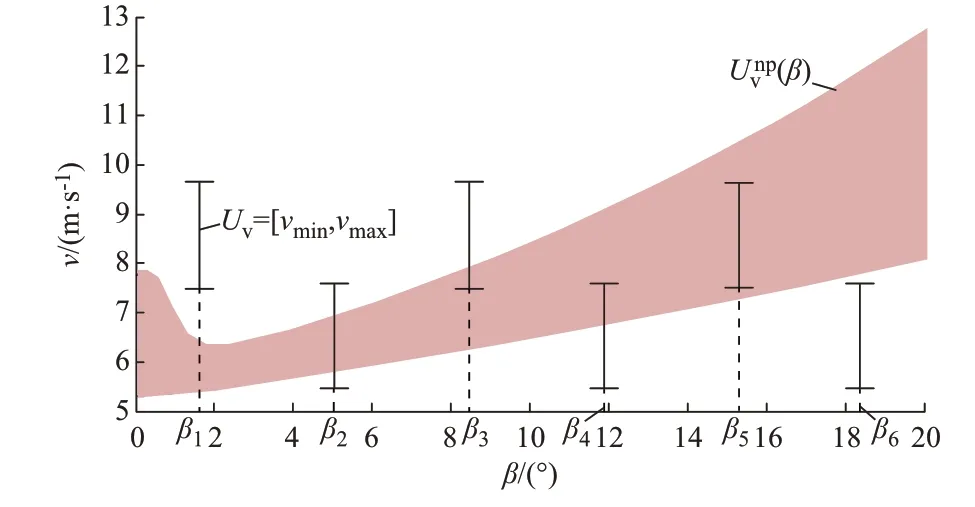
2.3 适配风速波动范围的桨距角确定


3 考虑Unp v 的APC 方法

4 实验验证与分析
4.1 风电机组动模实验平台
4.2 APC 控制性能的指标



4.3 实验结果分析
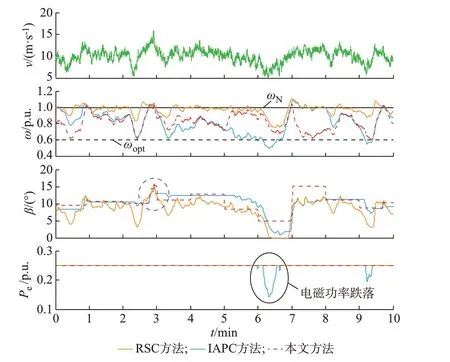

5 结语
