基于全局灵敏度分析的电气互联系统韧性提升方法

王 晗，侯 恺，刘晓楠，余晓丹，贾宏杰，杜 洁

（1. 国网郑州供电公司,河南省郑州市 450000；2. 智能电网教育部重点实验室（天津大学）,天津市 300072；3. 国网天津市电力公司电力科学研究院,天津市 300384）

0 引言

随着全球气候的加剧波动,极端自然灾害的发生愈来愈频繁,灾害的强度也愈来愈高。在极端灾害的冲击下,能源系统容易发生元件故障,威胁系统的安全稳定运行［1］。2011 年,西太平洋国际海域发生9.0 级地震,日本仙台以及附近岛屿发生大面积停电事故,燃气管道破裂引发多处火灾［2］。2020 年,台风“黑格比”导致中国浙江电网584 条线路停运,影响198.6 万户居民正常用电［3］。

为分析极端灾害带来的巨大影响和损失,文献［4-5］提出了韧性的概念,评估系统应对极端灾害冲击并快速恢复的能力。韧性指标可定义为系统功能损害部分与时间的积分,它同时考虑了系统抵御灾害的鲁棒性和灾后恢复的快速性［6］。文献［7］指出鲁棒性和快速性在韧性指标中所占的比重不同,建议考虑决策者对初始损失和恢复时间的侧重偏好。文献［8］认为输电网需要确保系统面临扰动时能足够坚强,相比快速性更侧重于鲁棒性。文献［9］从鲁棒性角度出发,采用系统负荷损失描述韧性水平,对于输电网和输气网耦合得到的电气互联系统而言是可行的简化指标。

韧性提升是韧性研究的关键。文献［10］提出了多微电网系统两阶段能量管理调度方法,实现灾后恢复阶段的供电最大化。文献［11］构建了一个系统拓扑重构模型,以指导制订灾后系统元件的修复序列。不同于微网调控和拓扑重构,元件强化着眼于灾前规划阶段,更适合侧重鲁棒性的电气互联系统的韧性提升。文献［12］基于三层鲁棒优化模型设计了识别和保护易受攻击元件的防御策略,提高了电气互联系统韧性。现有文献虽然对韧性提升方法开展了大量研究,但仍缺少对实施措施耗资与韧性提升效果之间关系的量化分析。

灵敏度分析能够定性或定量地评价参数不确定性对韧性指标的影响,包括局部灵敏度分析（local sensitivity analysis,LSA）和全局灵敏度分析（global sensitivity analysis,GSA）。现有研究通常应用LSA对元件进行排序,从而找到系统薄弱环节,指导制定韧性提升方案［13-14］。然而,LSA 只能描述单个参数的变化对韧性指标的影响程度,GSA 则可以分析每一个参数及参数之间相互作用对韧性指标的总影响［15］。GSA 已经广泛应用于生态模型和结构系统,但在韧性研究领域应用较少。此外,GSA 的计算方法Sobol 法是一种基于方差的蒙特卡洛模拟（Monte Carlo simulation,MCS）法［16］,存在可行性差、操作复杂耗时等问题。

对电气互联系统而言,韧性指标可用负荷损失期望简化描述,韧性未达标时可采取元件强化措施提升韧性。现有研究难以量化分析因元件强化成本的投入所带来的系统韧性水平的提升,无法服务于面向韧性提升的精细化规划。灵敏度分析方法具有解决该问题的潜力,但是主流的LSA 方法存在一定局限性。为此,本文提出了基于影响增量的全局灵敏度,并定量描述多元件失效概率变动对韧性指标的总影响,进而构建元件强化方案的全局寻优模型。

1 韧性理论基础

1.1 韧性指标

电气互联系统为跨区级能源输送网络,其韧性研究侧重系统抵御灾害的能力。本文将负荷损失期望作为电气互联系统的韧性指标［9］,该指标可以由状态枚举（state enumeration,SE）法求得,表达式为:

式中:R为韧性指标值；A为元件编号的集合,A={1,2,…,N}；card(·)为求集合中元素个数的基函数；N为元素个数；s为故障元件的状态集合；i和i′分别为发生故障和未发生故障的元件编号；pi为元件i的失效概率；pi′为元件i′的失效概率；Is为故障状态集合s的影响量,即负荷损失值。

作为SE 法的改进方法,基于影响增量的状态枚 举（impact-increment-based state enumeration,IISE）法将式（1）中的括号全部展开,并应用换元法对其进行数学变换,得到的表达式为［17］:

式中:ΔIs为故障状态集合s的影响增量；ns为故障状态集合s的故障元件个数；Ωk s为集合s的k阶子 集。

SE 法通常只枚举低阶故障状态以确保指标求解效率。这种情况下,式（1）中忽略的高阶项远小于式（2）中的高阶项。因此,IISE 法能够有效提高SE法的计算精度。当最高故障枚举阶数设定为J时,韧性指标的解析表达式为:

1.2 电气互联系统负荷削减优化算法

燃气电厂的技术现状成熟,应用前景广阔,是最常见的电气耦合设施。为便于分析,本文假定电气互联系统中只包含燃气电厂耦合设施。

电力子系统和天然气子系统通常由不同的公用事业公司运营［18］,故本文采用解耦优化框架计算故障状态下电气互联系统的最优负荷削减量,算法示意图见附录A 图A1。算法流程包括以下步骤:

步骤1:以各节点电负荷削减量之和最小为目标对电网进行优化,得到燃气电厂的出力,进而确定供气节点应提供的气负荷。

步骤2:以各节点气负荷削减量之和最小为目标对气网进行优化,得到燃气电厂供气节点的负荷削减量。

步骤3:若供气节点负荷出现削减,则根据削减量修改对应燃气电厂的出力上限,并返回步骤1；反之,判定算法收敛。

步骤4:根据电网优化结果和气网优化结果计算故障状态s的影响量,即系统总负荷削减量,表达式如式（5）所示。

式中:Pshed和Gshed分别为电负荷削减量和气负荷削减量；q为天然气的热值。

解耦框架将电气互联系统优化问题分割为更易于处理的电网优化模块和气网优化模块。针对电网优化模块,本文采用交流潮流模型计算最优电负荷削减量［19］。该模型能够充分考虑各种运行约束,且可以基于Matpower 工具包进行求解。针对气网优化模块,本文采用两阶段气网优化模型计算最优气负荷削减量［20］。此模型通过第2 阶段的非线性连续模型对第1 阶段的简化解进行修正,兼顾了模型精度与计算效率。

1.3 灾害模型

极端灾害主要包括地表灾害和地质灾害。其中,地质灾害能够同时打击电力系统和天然气系统,是电气互联系统最需要警惕的灾害类型。本节以最典型的地质灾害——地震为例介绍灾害模型。

震级和震中点描述了地震的自身性质,烈度则描述了地震在受灾区域各点造成的破坏程度。依据椭圆衰减模型,地震等烈度线可视为同心同向、层层嵌套的椭圆序列［20］。这些椭圆均以震中点为中心,在椭圆长、短轴方向上各点地震烈度表达式为:

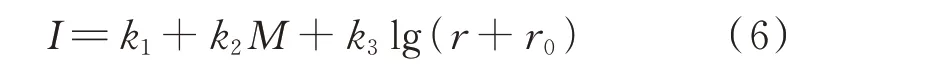
式中:I为地震烈度；M为地震震级；r为震中距；k1、k2、k3和r0为回归参数。

在已知震级和震中点坐标后,依据式（6）可以绘制地震烈度分布图,进而判断系统各元件所处烈度区。文献［20］介绍了变压器、输电线路和燃气管道的基于烈度的失效概率模型。据此可计算式（4）中的pi。极端灾害影响下,电气互联系统元件的失效概率大幅增加。一方面,地震可能致使输电线路和变压器受损,引发电网切负荷；另一方面,地震也可能致使深埋地下的燃气管道破裂,导致气网负荷切除和燃气电厂出力下降,进一步加重电网负荷损失。

2 面向韧性提升的全局灵敏度分析

2.1 基于影响增量的全局灵敏度

现有研究难以定量分析多元件失效概率变化带给韧性指标的整体影响。为此,本文以IISE 法为基础推导计算韧性指标的全局灵敏度。

由式（4）可知,韧性指标R即为元件失效概率数组（p1,p2,…,pN）的多元函数。数组（p1,p2,…,pN）与定义在N维超立方体[0,1]N上的点p相对应,故可将此多元函数记作R(p)。

定义Rj(p)为:

式中:L（p）为拉格朗日余项；θ为取值在区间[0,1]上的一个实数；Δp为各元件失效概率增量的数组,即Δp=（Δp1,Δp2,…,ΔpN）。

本文结合R（p）的函数性质对式（7）和式（8）进行化简,详细过程见附录B。根据化简结果可将R(p)改写为:

元件强化是通过升级材料、增设冗余等措施削减灾害下元件的失效概率,这对应着p∈[0,1]N从初始点p0向原点内收的过程。在此过程中,韧性指标R减小,系统韧性增强。因此,通常将韧性指标的下降值ΔR作为韧性提升强度的衡量标准,其表达式:

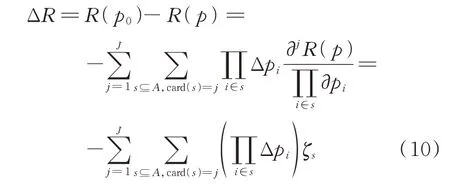
式中:ζs为全局灵敏度,描述了集合s中所有元件失效概率的相互作用对韧性指标的影响。

全局灵敏度的定量表达式进一步展开为:

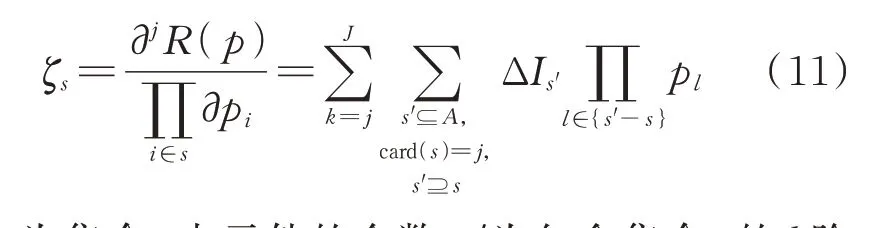
式 中:j为 集 合s中 元 件 的 个 数；s′为 包 含 集 合s的k阶元件集合；{s′-s}为集合s′与集合s之差；pl为元件l的初始失效概率。

为与IISE 法区分,本文将由式（10）和式（11）展开的相关研究记作基于影响增量的全局灵敏度分析（impact-increment-based global sensitivity analysis,IIGSA）法。值得一提的是,韧性指标J阶泰勒展开式的拉格朗日余项为0,这意味着IIGSA 法并未对IISE 法引入新的误差。

2.2 基于IIGSA 法的强化元件优选模型

元件强化的研究重心在于目标强化元件的选择。由于现有方法难以确定满足各类约束且全局最优的元件强化方案,本文基于IIGSA 法构建了强化元件的全局优选模型。

2.2.1 用于优化的ΔR表达式

韧性指标下降值ΔR由全局灵敏度ζs构成,能够准确描述多元件失效概率变化带来的韧性提升强度。然而,式（10）中的Δpi并非可优化变量,因此,ΔR表达式无法直接插入优化模型中。

非零的Δpi包含了2 层含义:第1 层含义指元件i被选择进行强化；第2 层含义表示元件i强化后的失效概率下降。本文假定对任一元件只采用一种强化措施,并引入0-1 整数变量,对Δpi进行优化范畴的表述,表达式为:

式中:hi为0-1 变量,强化元件i时hi=1,不强化元件i时hi=0；Δβi为 元 件i强 化 后 失 效 概 率 的 下降值。

特定强化措施下,Δβi为定值。例如,采用增设冗余强化元件时,Δβ即为元件失效概率与元件失效概率平方之差。

将式（12）代入式（10）中,得到的表达式为:

式（13）的高阶项会出现多个0-1 变量相乘的情况,需要引入新的0-1 变量替换消去连乘的hi,表达式为:

从而将式（13）转化为:

式中:ψ（s）为集合s的基数；Hs为0-1 变量,集合s中元件全部得到强化时Hs=1,反之Hs=0。

至此,本文得到了可用于优化的ΔR表达式,式（15）可以直接插入优化模型的目标函数或约束条件中,并结合实际需求优选目标强化元件。

2.2.2 强化元件的定量优选模型

设计元件强化方案时,既要关注方案的强化效果,也要定量分析成本-效益关系［22］。在实际应用场景中,有时需要考虑有限的强化预算,有时则需要考虑须满足的韧性标准［23］。现将各场景下的韧性提升需求归纳如下:

需求1:在预算限制场景下,充分利用有限的预算实现电气互联系统韧性的最大提升。

需求2:在达标约束场景下,花费尽可能少的元件强化成本,使得电气互联系统韧性指标达标。

实施元件强化方案后,韧性提升效果直观反映在韧性指标下降值上。因此,本文以式（15）为核心,分别构建了预算限制场景和达标约束场景下的强化元件优选模型。它们的目标函数和约束条件有所区别,但都能发挥IIGSA 法的全局分析优势。

1）预算限制型优化模型

成本预算限制场景下,优化目标为韧性提升效果最佳,约束条件以元件强化方案成本限制为主。该优化模型表达式为:

式中:ci为元件i的强化成本；Cmax为强化方案的预算成本上限。

2）达标约束型优化模型

韧性达标约束场景下,优化目标为元件强化方案成本最小,约束条件以韧性达标约束为主。该优化模型表达式为:

式中:R0为电气互联系统初始韧性指标；Rs为韧性指标的标准值。

2.3 元件强化方案全局寻优流程

基于IIGSA 法的强化元件优选模型可以得到最合适的目标强化元件集,为韧性提升规划提供参考。元件强化方案的全局寻优流程图如附录A 图A2 所示,具体步骤描述如下:

步骤1:基于灾害模型计算灾害场景下的电气互联系统元件失效概率pl。

步骤2:根据IISE 法求解电气互联系统初始韧性指标R0与各阶影响增量ΔIs。

步骤3:根据式（11）计算1 至J次全局灵敏度ζs。

步骤4:根据预采用的特定强化措施计算各元件的Δβ。

步骤5:根据应用场景选择预算限制型优化模型或韧性达标约束型优化模型。这2 类优化模型均为混合整数线性规划模型,可应用Cplex 求解。

步骤6:根据0-1 变量hi的优化结果确定目标强化元件,得到最优元件强化方案。

3 算例分析

3.1 算例介绍

电气互联测试系统［20］被引入一次地震场景的灾区作为算例。算例研究区域为250 km×300 km的长方形,其中,地震震中点坐标为（60 km,120 km）,震级为7.25 级。算例系统示意图如附录A图A3 所示,算例参数如表A1 和表A2 所示。

本文以此测试系统为例,对基于IIGSA 法的韧性提升方法进行验证。作为韧性研究方法的支撑数据,测试系统1 至3 阶元件故障下的最优负荷削减量被预先求出,各故障状态下的电负荷削减量及气负荷削减量如附录A 图A4 所示。

3.2 可行性验证

由于IIGSA 法以IISE 法为基础,需要验证IISE法求解韧性指标的精度及效率,并确定影响增量的最大枚举阶数。此外,IIGSA 法的最大优势在于全局视角。因此,还需要验证韧性提升研究中全局分析的必要性。最后,将IIGSA 法与现有韧性提升方法进行了对比分析。

3.2.1 IISE 法计算精度及效率验证

本文分别采用SE 法和IISE 法计算测试系统的韧性指标,并将MCS 法（当方差系数小于0.01 时判定收敛）的计算结果作为比照基准。几种方法的计算结果如表1 所示。表中,SE 法(N-J)和IISE 法(N-J)分别表示最高枚举至J阶故障的SE 法和IISE 法。

表1 系统韧性指标计算结果Table 1 Calculation results of system resilience index

由表1 可知,IISE 法的计算精度显著高于SE法,其计算时间又远低于MCS 法。IISE 法枚举至3 阶时,韧性指标计算结果已非常接近基准值,故本文设定故障状态最大枚举阶数J=3。

在IISE 法的计算过程中已经得到了影响增量,根据1 至3 阶影响增量数据可以直接求得各次全局灵敏度。

3.2.2 全局分析的必要性验证

本文采用增设冗余的措施强化部分元件（被强化元件的失效概率变为初始失效概率的平方）,并预设了3 个元件强化方案:方案1 为强化元件19 和23；方案2 为强化元件47 和49；方案3 为强化元件44、46 和47。

为比较元件强化方案的韧性提升效果,即韧性指标下降值ΔR,本文提出了以下3 种方法:

方法1:由式（4）计算实施元件强化方案前后的韧性指标,得到韧性指标下降值。此方法计算结果作为基准值。

方法2:计算各次全局灵敏度,并根据ΔR的解析式（10）直接求得韧性指标下降值。

方法3:根据式（10）单独计算方案中各元件强化后的韧性指标下降值,然后将其相加。

本文分别采用方法1、方法2 和方法3 计算3 个预设元件强化方案的韧性提升效果,计算结果如表2 所示。表中:ΔR1、ΔR2、ΔR3分别为通过方法1、方法2 和方法3 求得的韧性指标下降值。

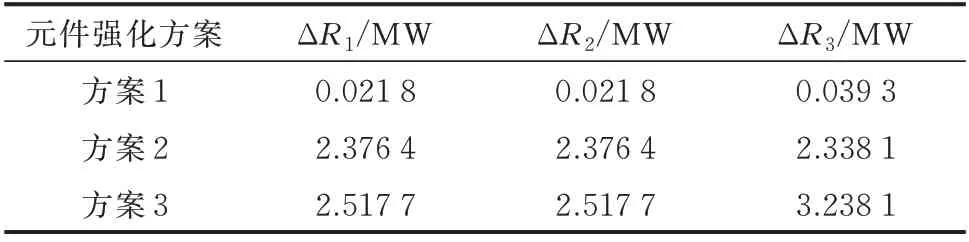
表2 韧性提升效果计算结果Table 2 Calculation results of resilience enhancement effect

方法2 与方法1 的计算结果一致,表明IIGSA法能够准确描述多元件失效概率变化带来的共同影响。方法3 的计算结果与方法1 差别明显,说明多元件失效概率变化的总影响并非单个元件失效概率影响的简单相加,凸显了韧性提升研究中全局分析的必要性。

分别采用电负荷损失期望值和气负荷损失期望值表示电力子系统和天然气子系统的韧性指标。应用方法1 计算元件强化方案1 至方案3 中电网的韧性指标下降值ΔRe与气网的韧性指标下降值ΔRg,结果如附录A 表A3 所示。方案1 强化元件均为电网元件,因此,ΔRe远高于ΔRg；方案2 和方案3 的强化元件均为气网元件,因此,总韧性指标下降值主要由气网侧的ΔRg提供。此外,只强化电网元件或气网元件都会给另一能源子网的韧性水平带来一定扰动。随着电气耦合程度的不断加深,这一扰动将不断放大。因此,有必要全局而非割裂地看待电气互联系统规划问题。

3.2.3 IIGSA 法与元件级指标法的对比分析

在不考虑经济性的情况下,规划人员往往需要在强化元件个数固定的限制下实现韧性的最大提升。本文分别采用IIGSA 法和元件级指标法［9］求取最优元件强化方案,并将强化元件个数的固定值从1 取至6。IIGSA 法和元件级指标法分别通过全局灵敏度优化模型和基于指标的元件强化次序确定目标强化元件集,2 种方法的详细流程如附录C 所示。

IIGSA 法与元件级指标法的计算结果如表3 所示。表中,Rnew为实施元件强化方案后的韧性指标,计算时间包括影响增量的计算用时和目标强化元件优选用时。在强化元件个数为1 或2 时,IIGSA 法与元件级指标法的优化结果一致；当强化元件个数大于2 时,2 种方法的目标强化元件集合出现了偏差,而且IIGSA 法的韧性指标下降值即韧性提升效果总高于元件级指标法。

表3 强化元件个数固定时的最优元件强化方案Table 3 Optimal component enhancement schemes when number of enhanced components is fixed

元件级指标法本质上仍是局部灵敏度的扩展方法。在强化元件个数不多时,元件级指标法尚且能够求得全局最优解,但随着强化元件个数的增加,该方法将难以给出最优的元件强化方案。IIGSA 法将各次灵敏度全部插入优化模型,建立了多元件失效概率变化与韧性指标下降值之间的准确关系式,故其全局寻优能力不受强化元件个数影响。

不同强化元件个数下,IIGSA 法的计算时间略有差异,而元件级指标法计算时间则保持不变。这是因为IIGSA 法优化模型的求解速度随强化元件个数变化存在一定波动。元件级指标法则直接确定了元件强化次序,按照此排序选择前列元件即可。2 种方法均以IISE 法指标为基础展开韧性提升规划,所耗时间主要用于影响增量的计算上,因此计算时间相近。此外,IIGSA 法相比元件级指标法还需要求解高次的灵敏度,因此计算时间稍长。

受限于固定的元件强化次序,元件级指标法无法适应实际应用中多变的韧性经济提升需求。而IIGSA 法优化模型能够根据不同的应用场景灵活配置待优化元件,与经济性的结合能力较强。针对预算限制场景和达标约束场景下的韧性提升,IIGSA法能给出最合适的元件强化方案。

3.3 元件强化方案优化结果分析

根据文献［24］,架空输电线路和燃气管道的造价分别为600 万元/km 和1 200 万元/km,并假定单台变压器造价为360 万元,由此可计算各元件强化成本。以下分别在预算限制场景和达标约束场景下对算例系统应用基于IIGSA 法的韧性提升方法。

3.3.1 预算限制场景下的韧性提升研究

本文采用基于IIGSA 法的预算限制型优化模型,分别计算预算上限Cmax为6 亿、12 亿、18 亿元时的最优元件强化方案,计算结果如附录A 表A4所示。

Cmax从6 亿元增至12 亿元时,目标强化元件集增加了元件44；而当Cmax从12 亿元增至18 亿元时,目标强化元件集中的元件15、1、17、44 被替换为元件47、8、11。这种基于IIGSA 法的目标强化元件调整不仅需要避免元件强化总成本超出预算上限,而且能够考虑不同元件失效概率之间的相互影响。此外,总强化成本非常接近预算上限,这表明IIGSA法能够充分调动预算额度,避免预算闲置。

同样是增加6 亿元预算,Cmax从6 亿元增加到12 亿元带来的ΔR提升幅度远小于从12 亿元增加到18 亿元。为分析预算上限Cmax与韧性指标下降值ΔR之间的非线性关系,本文对Cmax从0 到30 亿元均匀取值,取值间隔为1 亿元。然后,分别求出各预算上限取值对应的ΔR,从而得到两者的关系曲线如 图1 所 示。在Cmax位 于3 亿～4 亿 元 和12 亿～13 亿元取值段时,ΔR发生了跃升,这2 段跃升对应的元件强化方案变化也在图1 中给出,以表现IIGSA 法优化模型的全局调整效果。例如,Cmax为12 亿元时,待强化元件集合为{1,7,14,15,17,27,10,44}；而Cmax升 至13 亿 元 后,强 化 元 件 集 中 的 元件10、44 被替换为元件16、47。其中,元件47 的强化成本高达8.76 亿元,在预算上升后刚好能够计入强化,大幅拉高了韧性指标下降值ΔR。

图1 预算上限-ΔR 曲线Fig.1 Curve of maximum budget and ΔR

不难看出,如果将预算上限定在4 亿元或13 亿元附近有助于高效利用预算资金。这也为如何更好地设定预算上限给出了一条思路:先测算出如图1的韧性指标随预算变化的曲线,再根据该曲线与财务情况优化预算额度设定。

3.3.2 达标约束场景下的韧性提升研究

本文采用基于IIGSA 法的达标约束型优化模型计算韧性指标标准值Rs分别为1.2、1.0、0.8 MW时的最优元件强化方案,计算结果如附录A 表A5所示。

当Rs从1.2 MW 降至1.0 MW 时,待强化元件集增加了元件7、8；当Rs从1.0 MW 降至0.8 MW时,待强化元件集中的元件8 被替换为元件11、48。这种基于IIGSA 法的调整不仅能够保证韧性指标达标,还考虑了不同元件失效概率之间的相互影响作用。此外,优化结果的Rnew略低于韧性指标标准值Rs,且与Rs非常接近,这表明IIGSA 法能够多削减韧性指标,避免多余的成本开销。

同样是降低0.2 MW,韧性指标标准值Rs从1.2 MW 降至1.0 MW 增加的成本远低于从1.0 MW降至0.8 MW。为分析韧性指标标准值Rs与总强化成本之间的非线性关系,本文对Rs从0.5 MW到4.5 MW 均匀取值,取值间隔为0.1 MW。然后,分别求出各指标标准取值所对应的强化成本,从而得到两者的关系曲线如图2 所示。在Rs位于0.9～1.0 MW 或3.3～3.4 MW 取值段时,元件总强化成本急剧下降,这2 段跃变对应的元件强化方案变化也在图2 中给出,以表现IIGSA 法优化模型的全局调整效果。例如,Rs取0.9 MW 时,待强化元件集合为{7,8,10,27,47,5}；而Rs放宽至1.0 MW 后,刚好不再需要强化元件5。由此节省的强化成本对应了图2 中Rs在0.9～1.0 MW 段的成本剧降。

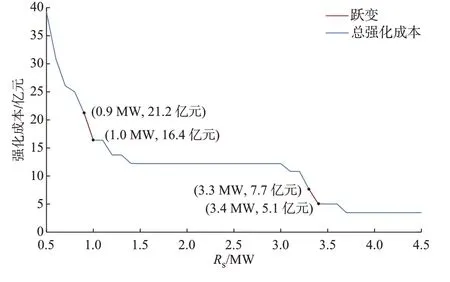
图2 强化成本曲线Fig.2 Curve of enhancement cost

由图2 可知,韧性指标标准值如果定为1.0 MW或3.4 MW,就能够避免不合理的强化成本增加,最大化达标的吸引力。值得一提的是,Rs为3.0 MW时,最优元件强化方案直接将韧性指标降至1.4 MW。这在图2 中体现为:在Rs从3.0 MW 降至1.5 MW 的过程中,元件强化总成本保持不变。

图1 与图2 中的曲线均为阶梯形,这主要是由于各个元件的强化成本是定值而导致有关成本的变化曲线不是平滑的。

4 结语

本文推导得到了韧性指标基于影响增量的全局灵敏度,并以此为基础构建了元件强化方案的全局优选模型,提出了量化提升韧性水平的IIGSA 法,并将其应用于电气互联测试系统中。主要结论如下:

1）与现有的局部灵敏度分析法相比,IIGSA 法能够准确描述多个元件失效概率变化带给韧性指标的总影响,即具备全局分析的优势。

2）全局灵敏度构成的韧性指标下降值可以插入优化模型中,以求得满足各类约束且全局最优的元件强化方案。

3）精准寻优的IIGSA 法可用于绘制阶梯形的预算上限-韧性指标下降值曲线和指标标准-强化总成本曲线,指导制定合理的预算上限或指标标准。

在规划周期内,电气互联系统可能遭遇的极端灾害场景存在不确定性。通过对各场景下的全局灵敏度赋权的方式可以将IIGSA 法拓展到基于潜在灾害场景集的韧性规划中。结构强化通过改变系统拓扑来提升系统韧性,与全局灵敏度的结合具有应用价值。此外,本文未考虑灾后恢复阶段,这一不足可通过向韧性指标加入赋权后的灾后恢复时间进行改进。

附录见本刊网络版（http：//www.aeps-info.com/aeps/ch/index.aspx），扫英文摘要后二维码可以阅读网络全文。