基于频域振荡模式的次/超同步分量可观可控分析
2023-02-27任健淼肖仕武
任健淼,肖仕武
(新能源电力系统国家重点实验室(华北电力大学),北京市 102206)
0 引言
随着可再生能源和电力电子设备在电力系统中所占比例不断增加,次/超同步振荡现象备受专家和学者们的关注[1-3]。中国新疆哈密地区多次发生直驱风电场次/超同步振荡,振荡发生时总是同时存在次同步和超同步两个互补的频率分量[4]。例如,在2018 年的哈密望洋台风电场的次同步振荡中,现场的电流监测结果表明,次、超同步频率为25.5 Hz 和74.5 Hz,次、超同步频率电流幅值为3.146 A 和10.75 A,次同步频率分量幅值明显不同于超同步频率分量[3]。因此,有必要解释次、超同步分量不相等现象的发生机理,并为抑制方案提供指导。
已有大量文献研究了风电机组并网的次/超同步振荡机理,分别从时域状态空间法[5]、频域阻抗特性[6-10]解释了次/超同步振荡的产生机理。由于阻抗特性可以用扫频的方式得到,适用于“黑箱”或“灰箱”控制结构的风电机组,这种研究方法获得了广泛应用[11],阻抗特性分为dq轴和正负序阻抗特性。文献[8]用谐波线性化的方法建立了单台直驱风电机组并网的正序阻抗和负序阻抗模型。文献[10]用相量图定性地解释了控制不平衡与频率耦合效应之间的联系,采用谐波线性化方法建立频率耦合的正负序阻抗模型并进行了验证。文献[12]针对风电场接入大规模电网的频域回路阻抗和节点导纳矩阵提出了频域可观性、可控性以及参与因子的研究方法,可以分析大规模电网振荡的产生机理及传播路径。以上文献分析了次/超同步振荡的产生机理及规律,但没有解释次、超同步分量相对大小不同及引起的原因。
次/超同步分量存在于相坐标系中,在相坐标系下的电网侧抑制风电机组次/超同步振荡时[13],往往需要选择目标频率进行模态滤波及抑制,发生次/超同步振荡时次同步分量谐波电流和超同步分量谐波电流都存在于系统之中[9-10],所以主要针对次同步频率分量还是超同步频率分量进行抑制便是需要讨论的重要问题。
本文首先在相坐标下建立风电机组并网系统的正负序回路耦合阻抗方程,计算其振荡模式及其在正负序分量上的可观可控度。根据正负序分量与次/超同步分量、dq分量之间的等价关系,解释了次/超同步分量幅值不相等的成因,随后定量推导得到次/超同步分量的可观度、可控度的理论表达式,实现了次/超同步分量的可观可控分析。最后,分析了影响次/超同步分量相对大小的影响因素,并进行了时域仿真验证。
1 直驱风电机组并网系统的正负序阻抗特性及其振荡模式分析
单台直驱风电机组并网如附录A 图A1 所示,直驱风电机组由风力机、永磁同步发电机、机侧换流器、直流电容器、网侧换流器组成,再通过升压变压器并入工频为50 Hz 的外部电网。在研究分析中可把发电机、机侧换流器等效为一个直流功率源。
直驱风机与电网的相互作用为系统在小信号下的动态行为,可以选择特定工况下的线性化模型分析此类问题[14-16],得到单机并网系统附录A 图A1 中风电机组和外部电网的等值阻抗特性,构成风电机组等值阻抗与电网等值阻抗的并联等效电路。其中,Lg为电网等效电感,iabc和uabc为风电机组的机端三相电压、电流信号。为了准确反映风电机组内部动态过程和相互作用,风电机组采用正负序耦合阻抗模型,考虑了频率耦合效应,其计算结果更精确,适用范围也更广。
风电机组的正负序耦合阻抗的建模过程已有文献进行了说明[7,10],具体的建模过程参考附录A,得到风电机组正负序耦合阻抗矩阵Zpns(s)为:

式中:Up(s)、Un(s′)分别为回路中加入的正序、负序扰动电压源,为系统输入扰动量[16];Ip(s)、In(s′)分别为正序、负序回路电流,s′=s-j2ω1,表示正负序回路之间的频率耦合关系,相对于2ω1呈频率互补关系,ω1为工频50 Hz 对应的角速度。
依据式(4)可以画出并网系统正负序回路下的等效图,如图1 所示。其中,受控源表示的是直驱风电机组频率耦合效应,而电压源表示的是加入的小扰动信号。基于直驱风电机组并网系统正负序回路阻抗方程,可以分析振荡模式在正序回路和负序回路中的次/超同步分量的可观、可控度。

图1 单台风电机组并网正负序电流回路Fig.1 Positive and negative sequence current circuit of grid connected with single wind turbine
根据并网系统正负序回路阻抗方程计算得到振荡模式,即为回路阻抗矩阵ZpnL行列式的零点[7,17],进而分析并网系统稳定性及其振荡特性。也可以通过电路节点导纳矩阵行列式的零点计算系统振荡模式,方法与回路阻抗一致[12,17]。考虑到单机并网系统网架结构简单,采用回路阻抗法分析更具优越性,对振荡电流的观测也更清楚。
风电机组并网系统振荡模式通过下式计算:

计算得到并网系统的振荡模式会有多个[7],具体数量与系统的阶数有关。其中,与次/超同步振荡相关的模式都是成对出现,并在振荡发生时呈现为主导振荡模式。单机并网系统的参数如附录A 表A1 所示,计算得到的振荡模式如附录A 表A2 所示,其中存在一对发散的互补频率振荡模式。
次/超同步振荡的主导模式是一对实部相等且虚部相加为2ω1的振荡模式。其中,振荡频率大于ω1的振荡模式称为超同步振荡模式,记为ssup;而振荡频率小于ω1的振荡模式为次同步振荡模式,记为ssub。
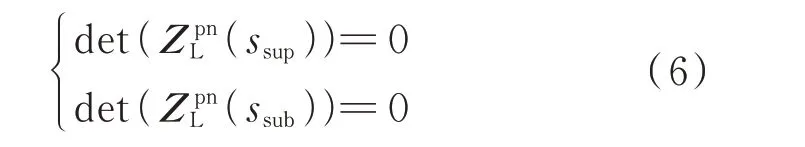
通过次/超同步振荡模式ssub、ssup的实部、虚部可以判断并网系统的稳定性和振荡频率。ssub、ssup的实部相等,次/超同步振荡模式的发散或收敛速度一样。
次/超同步振荡模式是一种从振荡频率范围形成的称谓,可以从正负序阻抗回路中得到,与正负序振荡模式是等价的。次/超同步振荡分量和正负序振荡分量存在着变换关系,正负序振荡分量与dq轴分量之间也可以等价变换。因此,次/超同步振荡分量、正负序振荡分量和dq轴振荡分量之间可以相互转换,而且振荡模式在次/超同步分量上的体现也可以通过正负序分量、dq轴分量进行研究。下面将利用三者之间的关系对次/超同步振荡分量幅值不相等的原因进行分析。
2 次/超同步分量与正负序分量、dq 轴分量之间的关系
2.1 正负序与次/超同步电气量之间的关系
直驱风电机组并入弱交流电网发生次/超同步振荡,会产生次/超同步分量的电流电压。当振荡的正序分量频率在50~100 Hz 的超同步频段,负序分量频率在-50~0 Hz 之间的次同步频段,此时负序分量变换到正序的频率为正,体现为两个正序频率分量,即两个都是正序的次/超同步分量。如果正序分量频率超过100 Hz,负序分量的频率为正,体现为负序分量形式[14]。因此,从理论上正负序分量可以等价表示为次/超同步分量。
角频率为ω的正序电压信号,也可以被写成负序形式:

式中:φ为振荡电压初相位。三相正序和负序电压的频率相反,相位相反。
基于回路阻抗方程计算得到次同步频段的负序电压可以变换成正序次同步电压,电流的对应关系也有相似的形式,表示为:
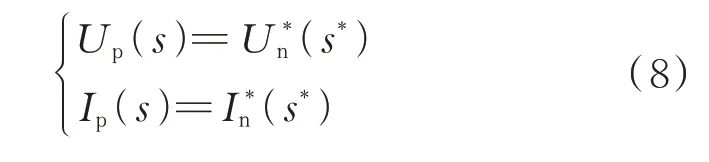
式(8)的物理意义是频率互补的正序相量和负序相量信号可以相互转化,可以用来分析以正序形式存在的次/超同步振荡分量以及振荡模式,即正负序分量与次/超同步分量之间具有等价变换关系。
以电流分量为例,将次/超同步振荡模式ssub、ssup代入正负序坐标系阻抗回路方程得到4 个正负序电流分量,把相同频率的电流分量相互叠加得到次/超同步分量电流,如图2 所示。

图2 次/超同步分量与正负序分量之间的关系Fig.2 Relationship between sub-/super-synchronous components and positive and negative sequence components
结合图2 可以得到正负序分量与次/超同步分量电流的关系为:

式 中:İsup为 超 同 步 振 荡 分 量 的 电 流 相 量;İsub为 次 同步振荡分量的电流相量。
根据式(9),对于次/超同步分量可观度、可控度的分析可以分为两步:首先,基于正负序阻抗得到正负序分量的可观度和可控度;然后,通过变换式(9)将正负序分量的可观度、可控度转化为次/超同步分量的可观度和可控度。
2.2 次/超同步分量与dq 分量之间的变换关系
已有文献基于dq坐标系讨论了正负序分量和dq分量之间的关系[8]:

定 义İd+=Id(ssup-jω1),İq+=Iq(ssup-jω1),İd-=Id(ssub-jω1),İq-=Iq(ssub-jω1),式(11)可 以简化为:

考虑到ssup-jω1和ssub-jω1是实部相等、虚部互为相反数的复数,而且d轴时域电流信号和q轴时域电流信号是实数信号,故而基于虚轴对称的两个复频率对应的相量值[18]应该满足:

将式(13)代入式(12)可以得到次/超同步电流和dq轴电流之间变换关系:
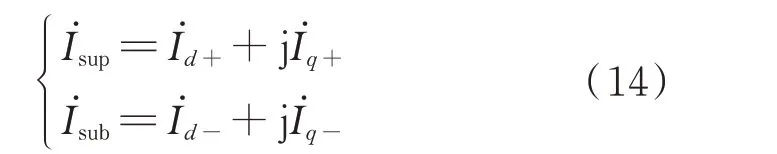
式(14)反映了次/超同步分量与dq分量之间的联系。
2.3 次/超同步分量大小在dq 坐标系上的反映
下面讨论当次、超同步振荡分量幅值不相等时dq轴电流相量应满足的数学关系式。设dq振荡分量的相量İd+=ad∠θd,İq+=aq∠θq,由式(14)可求出次、超同步分量之间的幅值差与dq分量之间的关系式为:

当θd>θq即d轴振荡电流分量超前于q轴时,相序下超同步振荡分量会大于次同步振荡分量;反之,当θd<θq即q轴振荡电流分量超前于d轴时,相序下超同步振荡分量会小于次同步振荡分量。图3形象地用相量图表示了次/超同步电流与dq电流之间的关系,依据dq电流的相位关系即可定性地判断次/超同步分量幅值大小的相对关系。

图 3 次/超同步分量与dq 电流分量相量图Fig.3 Phasor diagram of sub-/super-synchronous components and dq current components
以上分析只能解释次/超同步振荡分量的发生机理。下面将从正负序阻抗的角度定量描述可观度和可控度的计算方法以及物理意义,量化解释次/超同步分量大小不同的原因,并为次/超同步振荡的抑制提供理论根据。
3 振荡模式在次/超同步分量上的可观度和可控度定量分析
3.1 次/超同步振荡模式在正负序分量上的可观可控度
如图1 所示的单机并网系统被拆分成了一个正序回路和一个负序回路,由此便将一个电流回路拆分为正负序两个电流回路,从而可以将多节点多支路的可观可控分析方法[17]引入单机并网系统,便可以分析正负序分量的可观可控度。

风电机组并网发生次/超同步振荡时,正序、负序分量的频率相对于2ω1呈频率互补关系,即式中正序、负序分量受到频率互补关系的约束。
将式(16)代入式(17),并进行对角化矩阵变换,可以得到:

式中:J1(s)、J2(s)分别为与振荡模式相关的模式电流;V1(s)、V2(s)分别为与振荡模式相关的模式电压。
式(18)表明通过矩阵变换,正负序耦合回路方程可解耦为两个模式的回路方程。
回路阻抗矩阵的零点就是振荡模式,式(16)在振荡模式s=ssup处存在极点,而Hpn(s)和Wpn(s)均为非奇异矩阵,故而可以知道对角阵Λ-1(s)存在极点,即λ-11(s)或λ-12(s)存在极点。设振荡模式ssup存在于λ-11(s),即λ-11(ssup)=0。通过式(20)可以推导出振荡模式ssup在正负序电流的可观度和可控度。
由模式电流和模式电压的关系式(18)可知,若式(16)中的右特征矩阵可以表述成Hpn(ssup)=[h1,h2],左特征矩阵可以表述成Wpn(ssup)=[w1,w2]T,其中,h1、h2、w1、w2均为二维列向量。
1)可观度为ssup模式电流J1(s)对Ip(s)、In(s)的反映能力。依据式(20)可得:
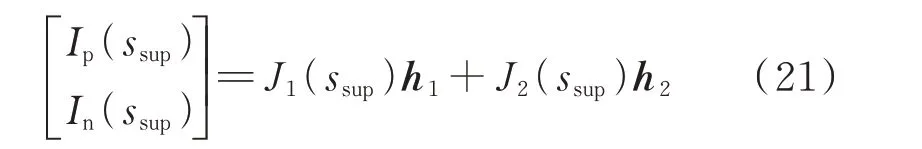
因为此时J1(s)为超同步振荡模式ssup的模式电流,而J2(s)不是,有J1(ssup)≫J2(ssup),忽略式(21)中J2(s)对系统的影响得到:

h1为超同步振荡模式ssup对正负序分量的可观度向量。
2)可控度为Up(s)、Un(s)对ssup模式电压V1(s)的控制能力。同理,依据式(19)可以得到:

式中:w1为正负序分量对超同步模式ssup的可控度向量。
以上便是正负序分量在超同步模式ssup的可观、可控度的定义及物理意义。由于次同步模式的可观、可控度和上面的分析过程是一致的,不再详述。
为了不失一般性,将正负序分量在超同步模式下的可观度统一成hsup(即上面分析的h1),可控度统一成wsup(即上面分析的w1)。与超同步模式相似,次同步模式ssub对应可观、可控度也可以分别被统一成hsub和wsub。
通过上面的表述,可以总结出如下:

由此,正负序分量对次/超同步振荡模式的可观度和可控度已经被求出,接下来使用式(9)将正负序分量转换为次/超同步分量,便可以讨论次/超同步振荡分量的可观度与可控度。
3.2 次/超同步分量可观可控度分析
上文依据正负序阻抗特性完成了对正负序分量的可观可控的分析,但是正负序分量与次/超同步分量有所不同,式(9)已经说明了它们是可以相互转换的,本节将把上一节的分析结果变换到次/超同步分量的可观性和可控性。
式(27)可以写成:
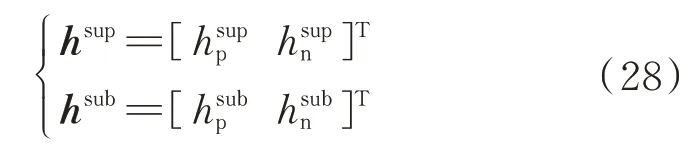


式中:osup、osub分别为超同步分量、次同步分量的可观度,它们反映了次/超同步振荡发生时超同步分量幅值与次同步分量幅值之间的相对大小关系。
将式(27)、式(28)代入式(29),可以得到次/超同步振荡分量对于超同步振荡模式的可观度:

直驱风电机组并网系统的总正负序耦合阻抗各元素满足如下关系[7,10]:
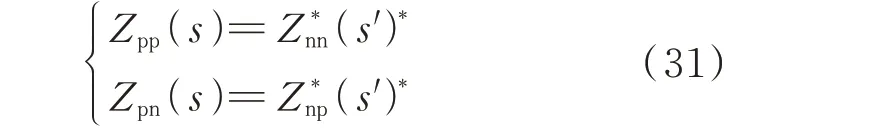
将式(31)代入式(30)得到次/超同步分量的可观度:
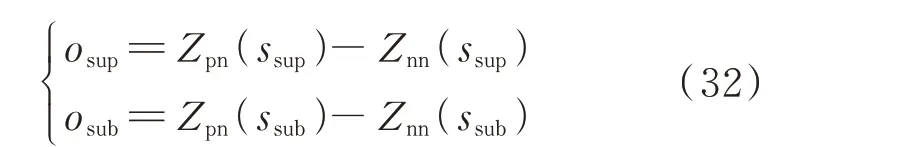
同理,对于次/超同步分量对次/超同步振荡模式处的可控度也可以推导出:

式中:csup为超同步分量的可控度;csub为次同步分量的可观度。它们反映了次/超同步振荡发生时超同步分量的控制信号与次同步分量控制信号对振荡模式的影响能力。
由式(32)和式(33)可以看出,导致次/超同步分量的可观度和可控度不相等的主要原因是阻抗特性在振荡模式ssup、ssub处的阻抗值不相等。基于单机并网系统,参数如附录A 第A1 节所示,得到的可观度表征阻抗Zpn(jω)-Znn(jω)、可控度表征阻抗Znp(jω)-Znn(jω)的幅值随频率变化曲线如图4 所示。由于可观度表征阻抗、可控度表征阻抗在次/超同步振荡频率处的阻抗值不相等,导致了次/超同步分量可观度、可控度不同。
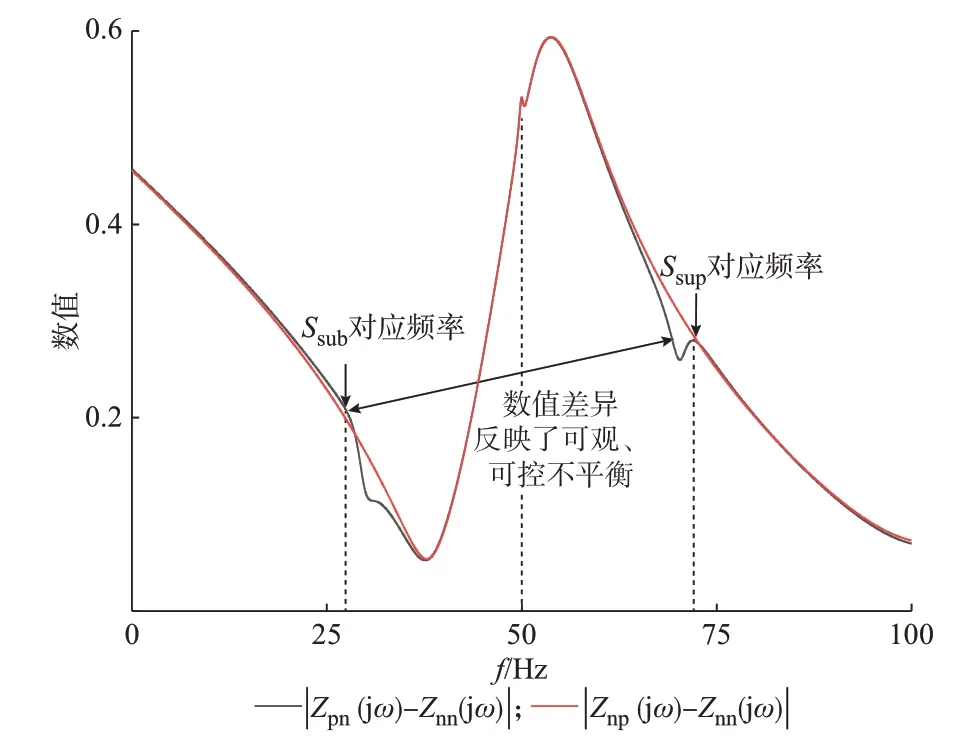
图4 可观度和可控度表征阻抗幅值频率变化曲线Fig.4 Amplitude frequency change curve of observable and controllable characteristics impedance

3.3 次/超同步分量的可观度和可控度的物理意义
虽然式(32)和式(33)已经可以将并网系统的可观度和可控度描述的很清楚,但是较为抽象。为了能更清晰地表述次/超同步分量的可控度和可观度,下面将对其物理意义进行讨论。
由式(22)可得:

如果次同步电压为Usub、超同步电压为Usup,次/超同步电压的表达式也与附录A 图A3 和式(9)的对应关系类似:
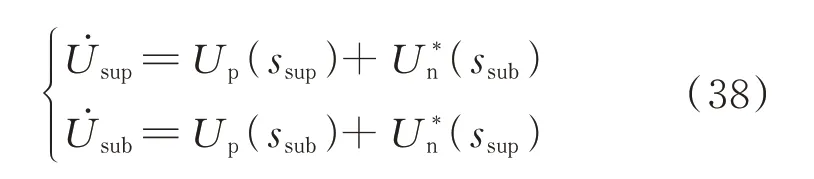
将式(34)至式(37)代入式(9)、式(38),可以得到:

式中:模式电流J̇=J(ssup)=J*(ssub),模式电压V̇=V(ssup)=V*(ssub)。
式(39)反映了次、超同步可观度,即在振荡发生时模式电流在次、超同步分量上的体现能力,这是与振荡时次、超同步振荡分量的幅值不等最相关的物理机理。式(40)反映了次、超同步可控度,即超同步控制信号与次同步控制信号对模式电压的控制能力。
3.4 次/超同步分量的可观比和可控比分析
式(32)可观度可以反映次/超同步振荡分量的幅值大小,式(33)可控度可以反映施加次、超同步控制电压对振荡模式的控制能力。为了更明显地反映它们的相对大小,定义次/超同步可观比和可控比分别为:

式中:χ为可观比,其物理意义是振荡发生过程中次同步振荡分量与超同步振荡分量的幅值比;γ为可控比,其物理意义是施加次/超同步控制电压对振荡模式的控制能力。特别地,当|χ|>1 时,次同步分量的幅值大于超同步振荡分量的幅值;当|χ|<1 时,次同步分量的幅值小于超同步振荡分量的幅值;当|γ|>1 时,输入次同步分量对振荡模式的影响程度比超同步控制分量信号强;当|γ|<1 时,超同步分量对振荡模式的影响程度比次同步分量强。
3.5 用dq 回路阻抗表示次/超同步分量可观比和可控比
基于正负序阻抗的形式展示了次/超同步分量的可观比和可控比,根据正负序分量和dq轴分量之间的关系,可以进一步在dq轴上表示次/超同步分量的可观比和可控比。假设风电机组并网系统的dq回路阻抗矩阵的形式为:
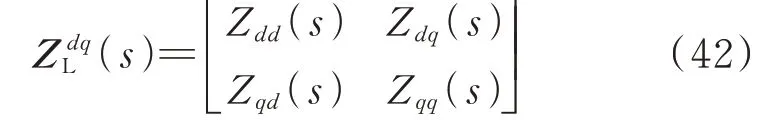
根据式(10),可得dq阻抗和正负序阻抗之间的转化关系为:

式中:s+=ssup-jω1=(ssub-jω1)*是在dq坐标系上求解出的虚部为正值的振荡模式。
根据式(44),可观比和可控比不再需要求得系统的正负序阻抗,而仅需通过dq阻抗便可以直接得到,这方便了可观比和可控比相关性质在dq坐标系上的应用。
3.6 次/超同步与dq 振荡模式及可观可控分析小结
当取s=ssup或s=ssub代入式(10)时,次/超同步振荡模式变换到dq轴上分别为ssup-jω1和ssubjω1。记s+=ssup-jω1,s-=ssub-jω1,依据频率耦合关系可以得到:

式(45)表明了次/超同步振荡模式变换到dq坐标系下的振荡模式是一对共轭的振荡模式,实部相等,振荡频率相反。也证明了次/超同步模式和dq坐标系下的振荡模式仅仅是频移的关系。结合式(13)、式(14)、式(43),做出dq分量与次/超同步分量的对应关系如图5 所示。

图 5 不同振荡模式与电气量之间的关系Fig.5 Relationship between different oscillation modes and electrical quantities
总结上述有关不同坐标系下振荡模式在不同电气量可观度的讨论。一方面,超同步振荡模式ssup在负序回路上的可观度与次同步振荡模式ssub在正序回路上的可观度是共轭的;另一方面,振荡模式s+与振荡模式ssup相对应,振荡模式ssup在正负序回路上的可观度可由振荡模式s+在dq回路上的可观度变换得到,故振荡模式在dq回路上的可观度也可以决定次/超同步分量的相对大小。
4 次/超同步分量可观可控度影响参数分析
在一般情况下直驱风电机组并网系统发生次/超同步振荡时,超同步分量大于次同步分量,即可观比χ<1,而对于可控比一般有γ<1,有必要具体找到导致次、超同步分量大小不一致的具体参数。本章将基于频域灵敏度法找到影响次/超同步分量相对大小及耦合关系的参数。频域灵敏度是目标变量对被研究参数在稳态运行点处的偏导数,反映了被研究参数对于目标变量的影响程度,故本文采用频域灵敏度方法来分析次/超同步分量可观比、可控比的影响因素[8]。
若α是待研究的参数,α0是参数的初始稳态值(参数见附录A 表A1)。由式(41)或式(44)可得可观比、可控比在参数α变化时频域灵敏度Kχ、Kγ的表达式为:
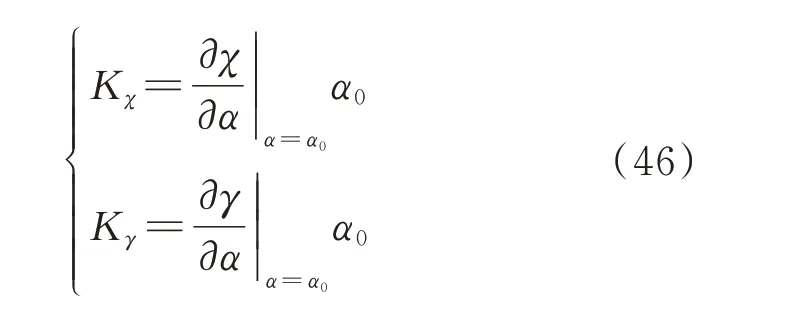
在直驱风电机组并网系统稳态工作点下,次/超同步分量可观比可控比灵敏度的计算结果如附录A表A3 所示。风电机组并网系统的控制参数与电气参数均会对可观比和可控比产生影响,而对于可观比灵敏度较大的参数,如锁相环积分时间常数、风机的输出功率以及电网的等效电感是造成次/超同步分量幅值不一致的重要原因。
根据灵敏度的正负性,可以知道除了稳压电容值C、电流环积分时间常数Ti和稳态电压U1外,其他参数的增大会使得超同步分量的可观度变得更大,也使得超同步分量的可控度变得更大。
从附录A 表A3 中可以看出,当锁相环带宽越大(锁相环比例系数Kp或锁相环积分时间常数Tp增大)、电压外环带宽越大(电压比例系数Kv或电压积分时间常数Tv增大)或直流稳压电容越小时,系统的可观比越低,也就意味着超同步分量比次同步分量将变得更大。
根据文献[10],锁相环带宽越大、电压外环带宽越大以及低直流稳压电容值会增强并网系统的频率耦合效应。但只凭借频率耦合效应的强弱无法解释系统可观比可控比的变化趋势。因此,本文所提的次/超同步分量可观可控分析方法具有独特的优势。
风电机组设计好并接入电网后,它的可观度和可控度与电网等效电感值Lg、稳态电压U1和稳态输出功率Pin有关。当风电机组输出较大的功率时,或当电网的等效电感更大时,或风电机组运行在低电压状态时,振荡分量中超同步分量会更大。对于可控比而言,风机在高输出功率、高运行电压、电网等效电抗大时,针对超同步进行抑制会更加合适。
5 仿真验证
5.1 振荡过程中可观度的验证
在PSCAD/EMTDC 搭建直驱风电机组并网系统电磁暂态时域仿真模型,参数如附录A 表A1 所示。根据式(6),通过正负序回路阻抗方程,理论计算得到超同步振荡模式和次同步振荡模式为:

在时域仿真模型运行1 s 时刻,向系统施加扰动使系统开始振荡,附录A 图A4 展示了振荡时a 相电流的时域波形,用Prony 处理该时域信号可以得到其发散速度为1.318 9 s-1,与理论计算得到的振荡模式实部的基本一致。图6 展示了a 相电流基于快速傅里叶变换(FFT)分析的频谱图,可以发现其振荡频率为73.50 Hz 和26.50 Hz,其与计算所得振荡模式的虚部的基本一致,说明理论计算振荡模式的正确性。
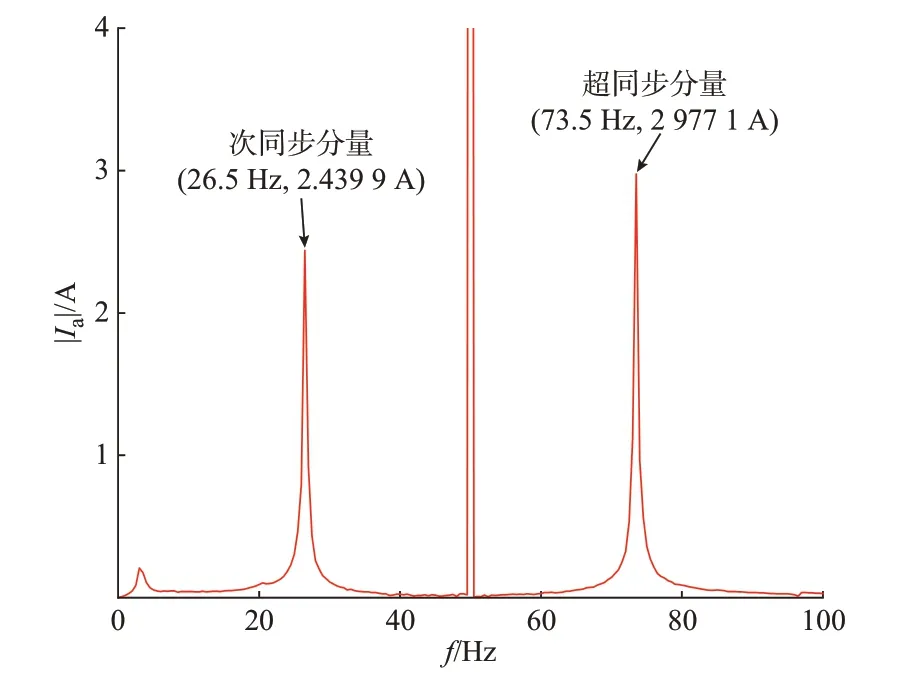
图 6 a 相 电 流FFT 分 析Fig.6 FFT analysis on a current of phase
根据式(41)和式(44)计算得到此时系统的次/超同步可观比理论值为χth=0.808 5。而在时域仿真中,次同步振荡分量与超同步振荡分量的幅值比为χact=0.819 6,两者的相对误差为1.35%,从而证明了理论计算可观比方法的正确性。
5.2 可控比的对比验证
5.2.1 测试原理
可控度反映了在次/超同步电压对振荡模式的控制能力。依据式(39)、式(40),如果在机端只串联注入超同步电压扰动U̇h,这时超同步电流为:

5.2.2 对比验证
根据附录A 表A3 所示的可控比灵敏度,发现电压环的比例参数对可控度的影响最小。为了在调整参数时尽量不改变可控度的大小,根据文献[8]的参数调整原则调整电压环的比例参数,将系统调整到稍稍收敛的状态,这是为了保证在注入谐波的过程中,系统的自激振荡不会因为电压扰动而被激发出来。
在系统稳定后在机端母线处串联谐波电压扰动源。第1 次,注入幅值为10 V、频率为73.5 Hz 的超同步电压扰动,应用滤波程序得到此时超同步电流信号的幅值为12.88 mA;第2 次,注入幅值为10 V、频率为26.5 Hz 的次同步电压扰动,得到此时超同步电流信号的幅值为10.34 mA。最后,依据式(49),可以得到如表1 所示的结果,从而验证了可控比理论的正确性。
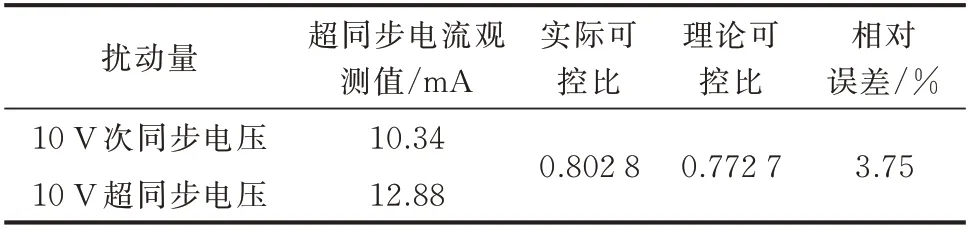
表1 可控比的对比验证Table 1 Comparison and verification of controllable ratio
6 结语
本文研究了直驱风电机组并网系统在振荡发生时次同步分量和超同步分量的可观度可控度。
1)建立了风电机组并网系统的正负序回路阻抗模型,计算次/超同步振荡模式及其在正负序回路上的可观度、可控度,分析出了阻抗特性在振荡模式ssup、ssub处的不相等是导致次/超同步分量可观度和可控度不同的主要原因。
2)基于dq轴分量与次/超同步分量之间的变换关系,分析得出d轴分量和q轴分量之间的相位关系导致了次/超同步分量的不相等,当d轴分量超前于q轴时,相序下超同步分量会大于次同步分量。
3)根据频域灵敏度分析了换流器及控制参数对次/超同步分量不平衡程度的影响规律,锁相环积分时间常数、风机的输出功率以及电网的等效电感是造成次/超同步分量幅值不一致的主要原因。
4)直驱风电机组在接入弱电网时发生次/超同步振荡时,应根据可控度的大小选择次/超同步频率进行抑制,一般超同步分量优先于次同步分量。
本文分析方法和结论也可推广应用于由多台风电机组组成的电力网络。另外,风电场内除了风电机组外,还有各种各样其他的电力电子设备,这些设备对系统可观度和可控度的影响并没有被本文所考虑,这将是下一步要研究的问题。
附录见本刊网络版(http://www.aeps-info.com/aeps/ch/index.aspx),扫英文摘要后二维码可以阅读网络全文。
