邻近既有建（构）筑物隧道爆破方案评价及优化方法

2023-02-24宋战平张艺多郭德赛张玉伟金琪

土木与环境工程学报 2023年1期

宋战平,张艺多,郭德赛,张玉伟,金琪

（西安建筑科技大学a.土木工程学院；b.陕西省岩土与地下空间工程重点实验室，西安 710055）

对于邻近建（构）筑物隧道，钻爆法仍是最常用的施工方法。然而，在爆破控制段施工过程中，爆破设计方案的优劣会直接影响爆破施工质量和成本，影响针对爆源所采取降震措施的实施效能[1]。因此，为保证爆破设计的合理性，学者们分别从不同角度进行了研究和讨论。针对爆破振动控制参数优化，李利平等[2]结合萨道夫公式及现场爆破监测数据，回归分析得到了竖向振速衰减模型，并以此优化掏槽爆破药量；刘冬等[3]采用数值模拟方法，对多孔微差爆破特征点振动规律进行探讨，为爆破控制参数设计提供了参考；Tian等[4]通过小波包分析，掌握了爆破地震波在地层中的传播规律，指导了振动控制参数的优化；梅比等[5]基于Adaboost-SVM组合算法实现了多种振动控制及影响因素的质点振动强度预测，为振动控制参数调整及最优爆破控制指标设计奠定了基础。针对质量控制参数优化，Xie等[6]基于深部岩体开挖抵抗应力和损伤传播方向的各向异性，提出了适用于深部岩体的掏槽设计方法；张国华等[7]借助DYNA软件将作用于损伤区内的振速转换为爆炸压力，并采用UDEC软件实现了对累计损伤范围的模拟预测；Monjezi等[8]使用人工神经网络技术确定了最佳光爆参数，保证了围岩的完整性；东兆星等[9]利用模糊数学理论对常用隧道掏槽方式进行了综合评判，分析了各方式的掏槽效果及适用条件；张建华等[10]基于层次分析法建立了评价指标体系，通过灰色关联分析确定各爆破设计参数最优解，得到了较为理想的爆破方案。在成本控制方面，张世雄等[11]基于模糊层次分析法（FAHP）对各爆破方案总成本进行了综合评价；戴俊等[12]基于模糊数学方法建立了爆破参数与爆后效果评价指标间的对应关系，实现了爆破成本和质量映射的最优参数选取。

上述研究主要是根据所依托工程的特点进行特定层面的爆破参数优化，尚未建立综合考虑振动危害、爆破质量及经济效益的设计参数评价及优化方法。鉴于以上问题，笔者利用数值模拟和非线性FAHP建立了邻近建（构）筑物隧道爆破方案评价及优化的新方法；结合实际工程，分阶段实现对受控对象的振动影响控制及开挖隧道的爆破质量和钻爆成本控制；将该方法应用于地宗隧道爆破控制段，并将方案各阶段评价与爆破结果进行对比分析，验证该方法在下穿既有建筑物爆破方案评价及优化过程的合理性和适用性。

1 爆破方案评价及优化方法的构建

爆破设计是隧道钻爆施工地震效应主动控制的关键，而隧道初始爆破方案多采用工程类比法得到，如何进一步结合工程特点对爆破参数进行优化，提高爆破控制洞段的施工效率是目前亟需解决的问题。针对此现状，笔者提出基于振动速度控制标准和非线性FAHP的爆破方案评价及优化新方法。新方法分2阶段实施：第1阶段采用数值模拟方法对基于工程经验确定的初始爆破方案的振动影响特征进行分析，结合邻近既有建（构）筑物爆破振速安全阈值要求对设计方案进行评价及优化；第2阶段针对第1阶段优化得到的满足振速控制标准的爆破方案，再从振动控制参数设计、质量控制参数设计及经济技术指标设计等层面对爆破设计进行综合评价及优化，得到满足爆破质量、爆破负面效应及爆破综合成本控制要求的方案。

1.1 基于振动速度控制标准的方案评价及优化

1.1.1 爆破荷载等效模型根据圣维南原理[13]，作用于等效弹性边界的复杂荷载形式可简化为合力相等的均布等效荷载，由此可确定爆破荷载的等效计算方法。不耦合或耦合系数较小的装药结构由式（1）计算得出群孔起爆等效荷载峰值，结合式（2）计算衰减至隧道轮廓线上的爆破荷载[14]。

式中：ρe为炸药密度，kg/m3；D为爆轰速度，m/s；γ为等熵指数；a为炮孔间距，m；r0为炮孔半径，m；r1为装药半径，m；le为单孔药柱累计长度，m；lb为炮孔深度，m；rb为等效边界至炮孔中心的距离，m；α为爆破荷载衰减指数。

爆破等效荷载的升压和作用时间与装药量、岩石力学性质、炸药距炮孔壁的距离等因素有关，可由经验公式（3）、（4）分别确定tr和ts[13]。

式中：tr为升压时间，ms；ts为荷载作用总时间，ms；r=R/r0，其中，R为弹性边界距装药中心的距离，r0为炮孔半径，m；μ和K分别为岩石的泊松比和体积压缩模量；Q为该段位炮孔药量，kg。

将爆炸应力波按不同比例均布于掏槽和非掏槽区各段等效弹性边界上，分别确定掏槽段和非掏槽段考虑微差效应的爆破荷载时程函数Pt(t)和Pe(t)[14]。

式中：n为该段位炮孔数；r为破碎区半径，m；l为等效弹性边界周长，m。

1.1.2 基于振速控制的方案评价及优化将爆破等效荷载时程函数导入Midas/GTS NX计算模型，可计算得到预留测点爆破全过程的振速时程曲线。根据振速时程曲线各段位峰值及变化规律，结合振动影响的安全判据，对周边建筑物的振动响应进行分析，由各段位振动响应特点确定降震措施，经逐步模拟优化得到符合振动危害控制要求的爆破参数。

1.2 基于非线性FAHP的方案评价及优化

1.2.1 爆破设计评价指标模型的构建根据爆破设计合理性评价目标及方案实施效果评价标准，结合爆破参数设置原则、文献资料和专家咨询结果[15]，将邻近既有建（构）筑物的隧道爆破设计评价模型分为振动控制参数设计、质量控制参数设计和经济技术指标设计3个一级评价指标，并由从属于一级指标的各因素构建二级指标，形成爆破设计方案评价的指标模型，见图1。所构建的爆破设计评价指标模型中，一级指标因素集为：U={U1，U2，U3}；二级指标因素集为：U1={u11，u12，u13，u14}，U2={u21，u22，u23，u24，u25，u26，u27}，U3={u31，u32，u33，u34}。

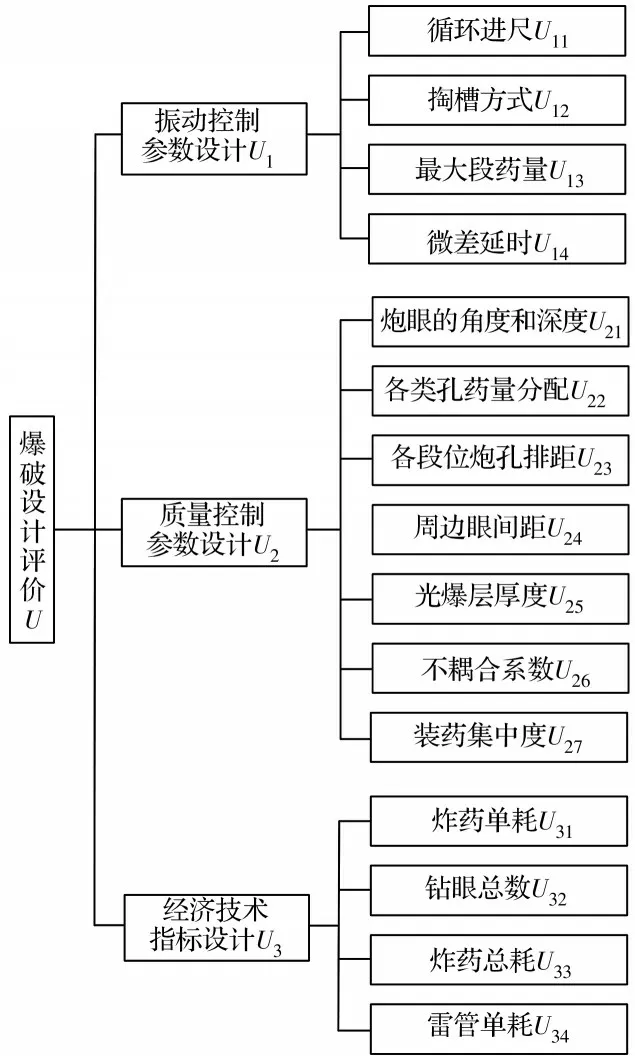
图1 爆破设计评价指标模型Fig.1 Evaluation index model for blasting design

1.2.2 权重向量确定根据1～9标度法评分准则，由相关专家分别对同级各个指标进行重要性比较，由两指标（包括自身）的重要性程度进行仿数量化，构建同级评价指标判断矩阵A，A=(aij)n×n且满足aij×aji=1，0＜aij≤1（i,j=1,2,…,n）。由式（7）求解最大特征根及其对应特征向量，并将特征向量W归一化得到权重向量W′。

式中：An×n为判断矩阵；W为最大特征值对应的特征向量；λmax为判断矩阵对应的最大特征值。

1.2.3 爆破设计评价指标权重的合理性检验判断矩阵阶数的增加会导致其一致性随机偏离概率增大，一致性偏离程度越大，所得权重的评价误差越大[16]。因此，判断矩阵最大特征值所对应的特征向量作为权向量是否合理，需通过一致性检验判断。由式（8）进行一致性指标计算，由式（9）计算检验指标C.R.，若C.R.＜0.10,则评价指标满足权重合理性检验标准。

式中：λmax为判断矩阵的最大特征值；n为判断矩阵的阶数；R.I.为随机一致性指标，如表1所示。

表1 R.I.对照表Table 1 R.I.comparison table

1.2.4 隶属度计算需从多个层面对隧道近接施工爆破设计方案的合理性进行讨论，如振动控制、光爆效果和掏槽效果等，而在爆破设计阶段，设计参数指标并无明确的合理性取值标准，难以定量地对其进行评价。专家评分法作为一种定性描述、定量分析的评价方法，可凭借经验，根据所制定的评分标准对无明确标准而难以量化的问题给出相应得分。笔者根据爆破设计评价特点建立评语集V，按照爆破设计方案的综合表现，将爆破设计评价等级划分为5级，即V=(v1,v2,v3,v4,v5)，如表2所示；采用逐级估量法对各指标因素进行模糊评价，构建指标因素uij的各评价等级隶属度向量Rij，如式（10）所示。为满足非线性模糊矩阵算子合成要求，需对隶属度取值进行模糊转换，rijm” =10×rijm，得到评语集与爆破设计评价指标模型各因素集对应的模糊关系矩阵Ri[17]。

表2 综合评价等级量化表Table 2 Comprehensive evaluation grade table

式中：rijm” ≥1，rijm” 为经模糊变换后的指标隶属度值；i为一级指标因素，i=1,2,3；j为二级指标因素；m为所属评价等级类别，m=1,2…5。

1.2.5 非线性模糊综合评判邻近既有建（构）筑物隧道爆破设计过程存在模糊性和不确定性，且振动控制指标参数的选定所呈现的突出影响效应对评价结果有一定的主导作用。因此，基于现场实际情况，由非线性合成算子替代线性加权算子反映部分爆破设计指标对评价结果的突出影响，并可将线性加权模型视为无振动控制要求时爆破设计方案评价的特例，进而通过模糊综合评价模型[18]计算结果向量N。

式中：“°”为合成算子；RN为2级评判矩阵。

根据振动控制指标对隧道爆破设计结果突出影响的特点，参考曹文贵等[18]对突出影响程度的量化标准，将各评价指标进行标度，得到突出影响系数向量Λ，记Λ=(λ1,λ2…λk)。非线性模糊综合评判中的合成算子（即式（12）中的“°”）形式为

其中

式中：win为指标因素权重；X为模糊转换后一级指标因素i所对应二级指标评价矩阵的第m列。

1.2.6 爆破设计指标参数综合评价及优化基于以上分析，考虑各专家评语间存在一定的模糊性，由式（14）将专家评语进行加权总分计算，转换为更加准确的量化分析结果。根据综合评价等级表可知，在计算总分≥75时，判定爆破设计参数合理，可由此确定爆破方案；当爆破设计评价结果得分＜75时，为突出主要影响评价结果指标，由式（15）将各指标隶属度取值与各评价等级得分结合，构建单指标评价向量f，由此确定单指标得分最小值fmin，并将fmin对应指标参数进行优化，待满足综合评价合理性判据时方可生成爆破方案。

式中：Nl为2级非线性综合评价结果的第l个元素；F为设计方案评价等级得分；RT为二级指标各评价等级隶属度向量组成矩阵R的转置；Sl为各评判等级对应得分，取值如表2所示；ST=[S1…S5]，为综合评价等级向量S的转置。

1.3 爆破方案评价及优化实现

由现场工况判断隧道爆破施工段是否需要考虑振动控制，有振动控制要求时，优先采用数值模拟方法对受控对象在等效爆破荷载作用下的振动响应进行评价，不满足规范要求的振速安全阈值则需利用数值模拟评价结果对振动控制参数进行优化，满足要求时，进入基于非线性FAHP的方案评价及优化阶段；无振动控制要求时，直接由非线性FAHP进行评价，此时振动控制指标的突出影响系数λi=1，满足合理性判据时即可确定爆破设计方案，不满足时，则有针对性地对影响评价结果的主要参数进行优化，而后再次进行非线性FAHP评价及优化，直至符合方案合理性判据。具体实现过程如图2所示。

图2 爆破设计方案评价及优化方法流程图Fig.2 Flow chart of blasting design scheme evaluation and optimization method

2 实例分析

2.1 工程概况

地宗隧道是新建安六高速铁路安六高铁站ALTJ-2段的重要节点工程，全长3 045 m，中间带宽3.6 m。爆破控制段里程为DK41+000～DK42+100，围岩分级为Ⅲ级（坚固性系数取8），隧道的埋深为49～57 m，与既有建筑物的水平距离为45～80 m。综合现场工况和工期要求，采用台阶法爆破开挖施工，并将上台阶单次进尺调整为2.4 m。

2.2 爆破设计及振动监测

2.2.1 初始爆破设计工程采用RJ-2防水乳化炸药，炮孔直径为40 mm，药卷直径为25 mm。采用台阶法钻爆施工时，上台阶仅以既有开挖面为自由面，而下台阶爆破时已具有足够的碎涨空间，引起的地震效应较上台阶大幅度降低。因此，仅对上台阶爆破设计进行评价及优化，具体设计参数如图3和表3所示。

表3 原方案上台阶爆破参数Table 3 Upper step blasting parameters of original scheme

图3 原方案炮眼布置图（单位：cm）Fig.3 Blast hole layout drawing of original scheme(Unit:cm)

2.2.2 爆破振动监测为验证第1阶段基于振速控制标准的方案评价过程的合理性，采用TC-4850爆破测振仪，在控制里程段DK42+000～DK42+100最接近隧道中心线的房角处布置测点，如图4所示。

图4 现场监测点布置图Fig.4 On-site monitoring point layout drawing

2.3 爆破方案评价及优化

2.3.1 基于振动速度控制标准的方案评价

根据隧道所处地质情况，将有限元计算模型简化为2 m厚的人工堆积土和78 m厚的灰岩，隧道为五心圆截面，洞径为15.2 m，隧道埋深为25.4 m，左右边界与隧道距离为3.5倍洞径，以减少边界效应的影响，如图5所示。围岩采用Mohr-Coulomb弹塑性模型，由于爆破动荷载的瞬时特性，材料的动强度与静强度存在着较大的区别。因此，根据静、动弹性模量与泊松比的转换公式对材料参数进行转换[19]，转换后的材料参数如表4所示。边界条件采用黏性阻尼边界，避免应力波在边界的反射对模拟结果产生影响，使应力波在地层中的能量衰减趋势和实际相符。

表4 岩体参数表Table 4 Rock mass parameter table

图5 有限元计算模型Fig.5 Finite element calculation model

隧道开挖轮廓边界的爆破等效荷载时程函数采用考虑微差效应的“群孔荷载模型”确定。由式（1）计算出炮孔壁上的爆破荷载峰值，根据式（2）计算出衰减到粉碎区边界上的爆破荷载，再以粉碎区为爆源，重复以上步骤，分别计算出掏槽段和非掏槽段等效至开挖轮廓面上的荷载峰值。在此基础上，由式（3）和式（4）分别计算出各段爆破荷载的升压和卸荷时间，最后结合各段位雷管延时及式（5）、式（6），分别得到掏槽和非掏槽段的荷载时程函数。其中，各段毫秒延期电雷管延时参考国产第一系列毫秒电雷管延期时间确定。将爆破等效荷载作用于数值计算模型，并添加与工程实际相对应的监测点，如图5所示。经有限元软件Midas/GTS NX分析计算，提取计算结果中模型C-3监测点三通道爆破全过程振速曲线，如图6所示。

图6 C-3测点模拟三通道振动时程曲线Fig.6 Simulated three-channel vibration time-history curve of measuring point C-3

综合考虑《爆破安全规程》（GB 6722—2014）及爆破负面效应随楼层升高的放大作用[20-21]，确定爆破控制段最危险点振速安全界限值为1.2 cm/s。由模拟结果可知，测点PPV为1.55 cm/s，大于安全界限值，且此测点位置距爆心68 m，大于爆破控制区建筑物最危险点的爆心距，因此,该方案不满足控制爆破要求。为确保受控对象安全，需对振动控制参数进行优化。由模拟的三通道速度时程曲线可知，监测点垂直方向（Z方向）振速大于水平方向（X方向）和切向（Y方向），且掏槽段振动的振速大于其他段位。由此可知，掏槽爆破是引起PPV大于振速安全阈值的主要原因，掏槽参数的设计是振动危害控制的关键。

2.3.2 爆破设计方案优化

1）根据模拟分析结果，原方案所采用的单级大楔形掏槽受到岩体的强夹制作用，单次消耗药量较大，引起的振动效应明显。因此，优化方案采用复式多级掏槽形式，减小掏槽最大段药量，且逐级增大掏槽区面积，以改善爆破振动控制效果及破岩效果。

2）在掏槽区布置一定量的空孔。由空孔为掏槽爆破过程提供岩石破碎膨胀的补偿空间，改变局部抵抗线，以改善掏槽效果。

3）在开挖轮廓增设小间距减震孔。介质的波阻抗特性是爆破地震波传播的基础，不同介质分界面具有不同的波阻抗特性，这将使地震波发生反射和透射，从而降低爆破地震效应影响。优化后的炮眼布置和爆破参数如图7和表5所示。

图7 优化方案炮眼布置图（单位：cm）Fig.7 Layout drawing of blasting holes for optimization scheme(Unit:cm)

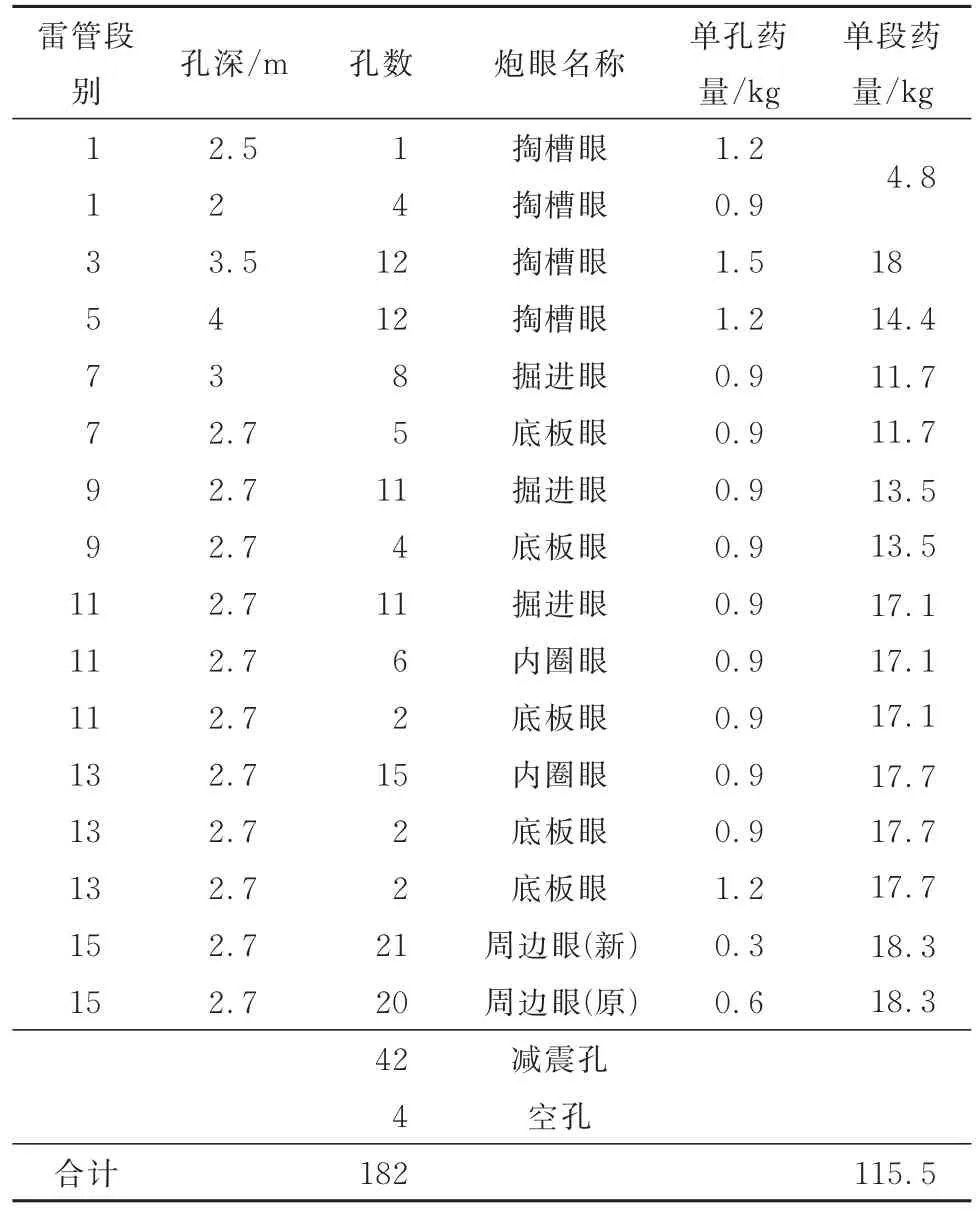
表5 优化方案上台阶爆破参数Table 5 Upper step blasting parameters of the optimization scheme

2.3.3 优化方案振速计算及评价

对优化方案进行数值模拟可知，监测点PPV为0.915 cm/s，小于设定的振速控制标准。根据夏祥[22]等和凌同华等[23]的研究成果，隧道围岩中存在软弱夹层、节理裂隙等地质现象，此类地质现象的存在会导致应力波能量耗散更为明显，而有限元计算所采用的地质模型为理想化的均质各向同性地层，未能考虑节理裂隙等因素的影响，导致模拟振速相较于实测值偏大。由以上分析可知，优化方案符合爆破段振速控制要求，可通过非线性FAHP对爆破设计指标进行下一阶段的综合评价。

2.3.4 基于非线性FAHP的方案评价及优化

1）权重计算。根据地宗隧道DK42+000～DK42+100里程段爆破施工特点，根据10位专家对各级指标做出的评价结果建立判断矩阵。通过MATLAB程序进行判断矩阵最大特征值λmax和对应特征向量的求解，经一致性检验和归一化得到各级指标对应权重。

第一级指标权重W′=[0.461,0.319,0.220]

第二级指标权重

振动控制参数设计：W1” =[0.281,0.320,0.245,0.153]

质量控制参数设计：W2” =[0.138,0.121,0.107,0.158,0.202,0.179,0.095]

经济技术指标设计：W3” =[0.341,0.265,0.232,0.162]

2）隶属度计算。结合爆破设计方案的评价等级，采用专家打分法对地宗隧道爆破控制段爆破设计方案的二级设计指标参数进行打分，优化方案上台阶炮孔布置及开挖参数见图7和表5，得到各指标所对应评语集的隶属度；通过公式rijm” =10×rijm将其转换为可进行非线性模糊综合计算的评判矩阵。

振动控制参数设计中各指标形成的非线性模糊评判矩阵为

质量控制参数设计中各指标形成的非线性模糊综合评判矩阵为

经济技术指标设计中各指标形成的非线性模糊综合评判矩阵为

3）确定指标的突出影响程度系数。根据地宗隧道爆破控制段实际需求，结合突出影响系数取值参考表，确定爆破设计评价指标所对应的突出影响系数，如表6所示。

表6 评价指标突出影响程度系数Table 6 The prominent influence degree coefficient of the evaluation index

4）非线性模糊综合评判。基于以上步骤，得到非线性评判矩阵R1～R3对应的突出影响程度系数向量Λ1～Λ3，利用式（12）进行一级非线性模糊综合评判，可得到爆破设计评价指标中二级指标所对应的评判结果向量Ni。以振动控制参数设计指标为例，突出影响程度系数向量为Λ1=[3.5,4.0,3.0,2.0]，则λ=max(3.5,4.0,3.0,2.0)。一级非线性综合评判过程如下：

同理，得到地宗隧道DK42+000～DK42+100段爆破方案评价中其他二级爆破设计指标所对应的1级非线性模糊综合评判结果向量分别为

由一级评判结果向量Ni构建新的单因素评判矩阵RN=[N1N2N3]T，并通过式rijm” =10×rijm进行模糊转换得到R′N。将一级指标权重、模糊评判矩阵和一级爆破设计评价指标所对应的突出影响程度系数向量Λ=[4.0,3.5,2,2.5]带入式（12），进行二级非线性综合评判，得到结果向量N。

由式（14）和式（15）分别计算方案综合评价量化得分F和单指标评价向量f。

根据加权计算确定最终设计方案得分为79.2，满足评价方法设定的方案合理性标准，且由单指标评价向量最小值fmin可知，影响设计效果的主要指标为爆破经济技术指标中的炮孔总数。相比于原方案，优化方案增加了掏槽区空孔和沿轮廓线布置的减震孔，增加了钻爆施工成本。而增设空孔是为了满足爆破控制要求，消减爆破振动负面效应对受控对象的影响，保证爆破控制段施工安全。对比优化前后爆破参数可知，优化后掏槽眼最大段位的药量较原药量减少了25%，上台阶总药量减少了0.7%。为满足控制爆破要求，优化方案采用三级复式楔形掏槽及增设减震孔减少爆破振动效应对周边建筑物的影响，且优化后模拟测点PPV较原方案降低了41.2%，符合规范要求。

3 监测和爆破效果分析

3.1 监测与数值模拟对比分析

由图8中Z方向模拟和实测振速对比可以看出，各段位模拟与实测振速的总体衰减趋势基本一致，波峰和波谷出现的数量和时间也较吻合；测点PPV出现在第3段位，为掏槽区爆破段位，引起的振动强度比其他段位更强烈，这与陈明等[24]的研究一致；测点振速峰值模拟值（0.915 cm/s）大于实测值（0.86 cm/s），但均小于振速阈值（1.2 cm/s）；大部分段位PPV模拟值均稍大于实测值，这是因为除模拟地质模型与现场地质差异造成的影响外，优化方案的荷载等效及模拟过程并未考虑掏槽区空孔及减震孔对地震波能量的耗散作用，这也使模拟结果略大于实测结果，但对爆破控制段爆破方案优化，能使评价和优化结果趋于保守，减少爆破测试次数，提高施工效率。

图8 C-3测点Z方向模拟和实测振速对比Fig.8 Comparison of simulated and measured seismic velocity in the Z direction of measuring point C-3

由图9中各测点三向实测和模拟PPV对比分析可知，随着爆心距的增加，Z方向实测和模拟PPV呈衰减趋势，但大于X和Y方向的PPV；各监测点PPV模拟值均大于或接近实测值，因此，采用数值分析方法能够很好地指导爆破设计评价及优化，提高隧道邻近既有建（构）筑物洞段的施工效率。

图9 各测点三向实测和模拟PPV对比Fig.9 Comparison of measured and simulated PPV in three directions at each measuring point

3.2 爆破效果

根据现场统计可知，优化方案实施后隧道最大线性超挖为15 cm，局部欠挖量小于5 cm，炮孔痕迹保存率大于80%；在保证原循环进尺的基础上，炮孔利用率达到了91%，提高了隧道近接施工效率，降低了该段的防护成本及爆破总成本。由此可以看出，该方法建立的方案合理性评价和优化过程及评定判据能够满足实际工程的需要，保证了爆破控制段施工过程中爆破振动影响控制、爆破质量控制及成本控制的效果。