基于MATLAB的滚柱活齿传动滑动特性研究
2023-02-24王冉王士军杜雅宁齐娜郑苏芮
王冉 王士军 杜雅宁 齐娜 郑苏芮
(山东理工大学机械工程学院,山东 淄博 255000)
滚柱活齿传动与行星齿轮传动、谐波传动和RV传动相比具有很多优点,如结构紧凑、传动比范围广、啮合度高、承载能力大、传动效率高和制造成本低[1]。随着活齿传动技术不断发展,逐渐被广泛应用于工业自动化、数控机床、卫星技术、工业机器人和数控机床等领域。因此,研究滚柱活齿传动是一项具有巨大应用前景的研究。滑动率和滑滚比作为滚柱活齿传动的重要参数,与传动效率和活齿啮合过程中的磨损密切相关,然而针对活齿传动相关的滑动率和滑动比系统性研究非常少。因此,研究设计参数对滚柱活齿传动的滑动率和滑滚比的影响变得越来越重要。
在目前的研究中,滚柱活齿传动的研究主要讨论中心轮齿形设计、传动特性分析、啮合刚度及承载性研究、啮合建模与仿真。宜亚丽等提出一种计算对数修形复合滚柱活齿啮合变形量的方法,分析了不同填充度对滚柱活齿啮合刚度的影响规律,并通过有限元分析对啮合处等效应力图进行了对比分析[2]。王志刚等建立了滚柱活齿传动平移-纯扭转耦合动力学模型,建立系统非线性动力学微分方程,通过改变参数偏心距和啮合阻尼,分析了参数变化对系统非线性动态的影响[3]。韩晓娟等提出了一种新型可实现任意齿差数的活齿传动,推导出中心轮齿廓方程,并对中心轮齿廓曲率、重合度和压力角进行了影响因素分析[4]。Kato K提出了一种单球传动活齿减速器,提高了能量效率,减少了传动滑移,简化了机构设计[5]。李勇进等用“等效机构法”推导了二齿差滚柱活齿传动的啮合曲线,提出了用矢量法求解激波凸轮中心轮实际齿廓线的方法,分析了不同参数修形方式与中心轮实际廓线曲率的关系[6]。陈杨等结合活齿啮合原理,对滚柱活齿传动的啮合副进行研究,建立相关啮合方程,采用可视化编程进行了滚柱活齿传动的建模与仿真[7]。张帅等针对二齿差纯滚动活齿内齿圈提出基于UG NX设计平台的三维数字化设计与加工的方法,并进行了建模与仿真,提高了工作效率[8]。
基于滚柱活齿传动的研究不少,但关于滚柱活齿的滑动特性很少有人研究。在本文中,通过结构特点和工作原理推导出滚柱活齿传动的数学模型和运动学模型[9-10],基于MATLAB软件分析了设计参数激波器半径、活齿半径、传动比和偏心距对滑动率和滑滚比的影响。
1 滚柱活齿传动的运动学原理
滚柱活齿传动主要有4个部分组成:激波器H、滚柱活齿G、中心轮K和活齿架M,如图1所示。
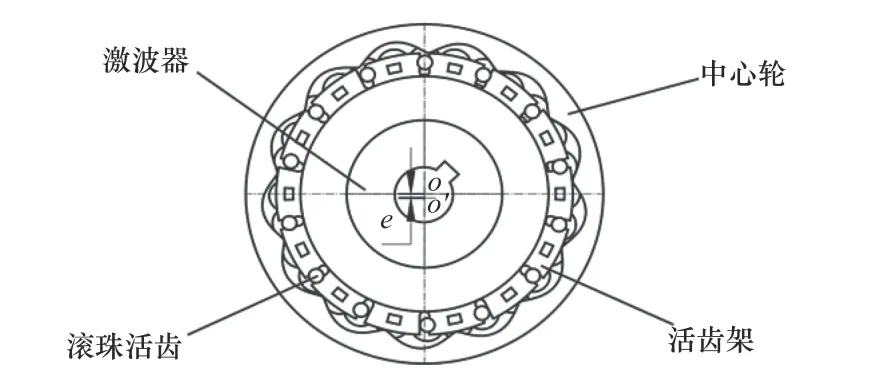
图1 滚柱活齿传动结构图
在滚柱活齿传动中激波器采用偏心凸轮,本文的研究对象中心轮是固定的,中心轮、活齿架和激波器是运动部件,利用机构转换法,假设给活齿施加一个与其周向角速度大小相等方向相反的角速度,此时活齿在活齿槽中作上下往复运动,设激波器的角速度为ωH,中心轮的角速度为ωK,滚柱活齿的角速度为ωG,根据三者的运动关系可以计算出传动比如式(1)所示。
本文的中心轮是固定的,激波器作为输入带动滚柱活齿转动,在活齿架和中心轮的约束下,滚柱活齿驱动活齿架输出角速度,其中ωK为0,偏心凸轮作为激波器通常为一齿差结构,计算传动比如式(2)所示。
式中:ZK为中心轮齿数;ZG为活齿齿数;“+”表示同向传动;“-”表示反向传动。
滚柱活齿传动的中心轮齿形设计对整个结构是十分重要的,通常需要根据结构的设计参数来确定,首先根据激波器和活齿的运动轨迹确定滚柱活齿的运动曲线方程,中心轮的齿廓曲线则为滚柱活齿的外包络曲线。
如图2a所示为滚柱活齿传动结构简图,在OXY坐标系中已知中心轮固定,激波器作为输入构件以某一角速度顺时针匀速旋转,滚柱活齿在激波器的作用下与中心轮啮合,在中心轮的约束下推动活齿架以恒定角速度顺时针旋转。
设滚柱活齿中心曲线的径向矢量OM=p,激波器半径为Rd,激波器的偏心距为e,活齿的半径为r。确定参数后可以得到中心轮理论齿廓线方程s-s方程为
式中:p为活齿中心的径向矢量可以用方程表示为
式中:θH为激波器的转角;θG为滚柱活齿的转角。
如图2b所示,中心轮实际齿廓线s′-s′为中心轮理论齿廓线的外等距线,α为y轴与s′-s′法线在啮合点的夹角。中心轮的工作齿廓线可以表示为
通过包络原理和如图2所示结构分析得到中心轮理论齿廓线s-s和实际齿廓线s′-s′进而确定具体设计参数,如表1所示为本文研究的滚柱活齿传动基本设计参数。

表1 滚柱活齿基本设计参数
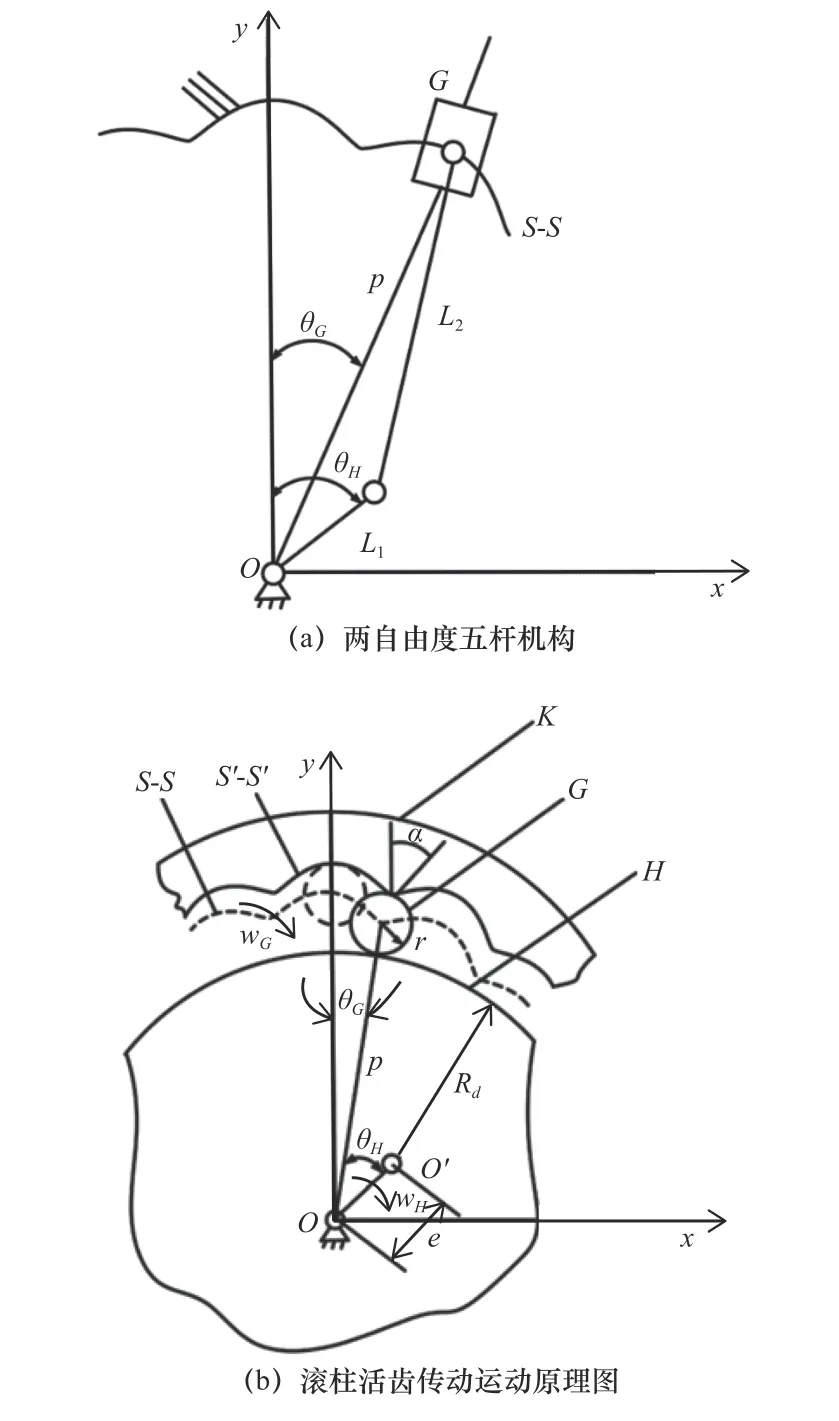
图2 滚柱活齿传动运动学模型
2 滚柱活齿传动滑动模型的建立
滚柱活齿传动由两个高副和一个低副组成,高副在运动过程中因接触点切向速度不同会产生相对滑动。滚柱活齿和中心轮之间的啮合状态是滚动与滑动并存的,滑动状态的增加会产生较多的摩擦,造成运动构件的损耗、传动不稳定和传动效率低等问题。解决上述问题最好的方式就是提高滚柱活齿在工作过程中的滚动状态。
目前国内外文献中对滑动率的研究非常少,本文基于对一般曲线的滑动率和滑滚比的研究结合滚柱活齿的结构特点,将运动过程中滚柱活齿与中心轮的啮合点相对滑动速度和切向速度的比值定义为滑动率。
式中:V1和V2分别为啮合点1和2处的切向速度;S1和S2分别为啮合点1和2的滑动率。
滑滚比可通过下式计算得到:
以滚柱活齿为研究对象,将滚柱活齿的速度进行分解:一是滚柱活齿在激波器驱动和中心轮齿形的约束下作圆周运动,此时的速度为VGg;二是滚柱活齿在活齿槽围绕滚柱销作自由转动,此时的速度为VGt;三是滚柱活齿在活齿架内作上下往复运动,此时的速度为VGn,这3个方面的速度可用下式计算:
式中:VHt=VG/sinδi,VG=qωH,ωH=iωG,δi=π/2-ηi,μi=π-δi-γi,φi=2γi-ηi,
在滚柱活齿运动过程中有两个方面会产生滑动,一方面为激波器与滚柱活齿之间,一方面中心轮与滚柱活齿之间。如图3所示建立了滚柱活齿传动滑动模型,假设激波器和滚柱活齿在啮合点N2处为纯滚动接触,中心轮与滚柱活齿在啮合点N1处运动规律不同又相互制约,因此中心轮与滚柱活齿之间一定会产生相对滑动。根据啮合原理和一般曲线的滑动率公式确定计算公式。
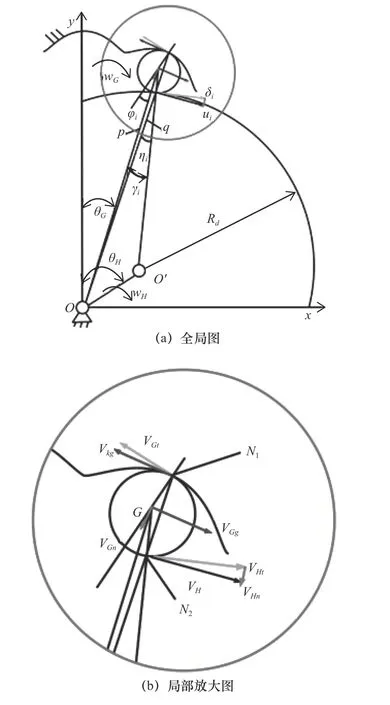
图3 滚柱活齿传动滑动模型
中心轮滑动率S1计算公式为
滚柱活齿滑动率S2计算公式为
滚柱活齿传动滑滚比S3计算公式为
式中:VKg=VGt。
3 参数对滑动率和滑滚比的影响分析
通过上述建立的滑动模型和方程,利用MATLAB软件编写程序,建立数值建模仿真[11],分析滚柱活齿传动设计参数激波器半径Rd、滚柱活齿半径r、激波器偏心距e和传动比i对滑动率和滑滚比的影响规律。
在保证其他设计参数不变的情况下,研究激波器半径Rd对滚柱活齿传动滑动率和滑滚比的影响,将激波器半径从55 mm增加到75 mm,每次增加5 mm,经过数值建模分析得到激波器半径对滚柱活齿传动滑动率和滑动比影响如图4所示。
由图4a可知,当活齿转角θG从0逐渐增加到0.448 7 rad时,激波器转动一圈,滚柱活齿完成从齿根到齿顶再次回到齿根的整个运动过程,中心轮滑动率S1先增大后减小,滑动率的变化率先增大后减小,在齿顶滑动率的变化率达到最小,在滚柱活齿和中心轮的啮合点处,中心轮滑动率的变化率最大。当激波器半径增加时,中心轮滑动率峰值增大,激波器半径每增加5 mm,中心轮滑动率峰值增大约0.21%,滑动率变化趋势越来越平缓。
由图4b可知,随着活齿转角θG从0增加到0.448 7 rad,活齿滑动率S2先减小后增大,活齿滑动率变化率先增大后减小,在啮合点处滑动率变化率最大,在齿顶处变化率最小。随着激波器半径每增加5 mm,活齿滑动率峰值减小约6.67%,滑动率变化趋势越来越平缓。
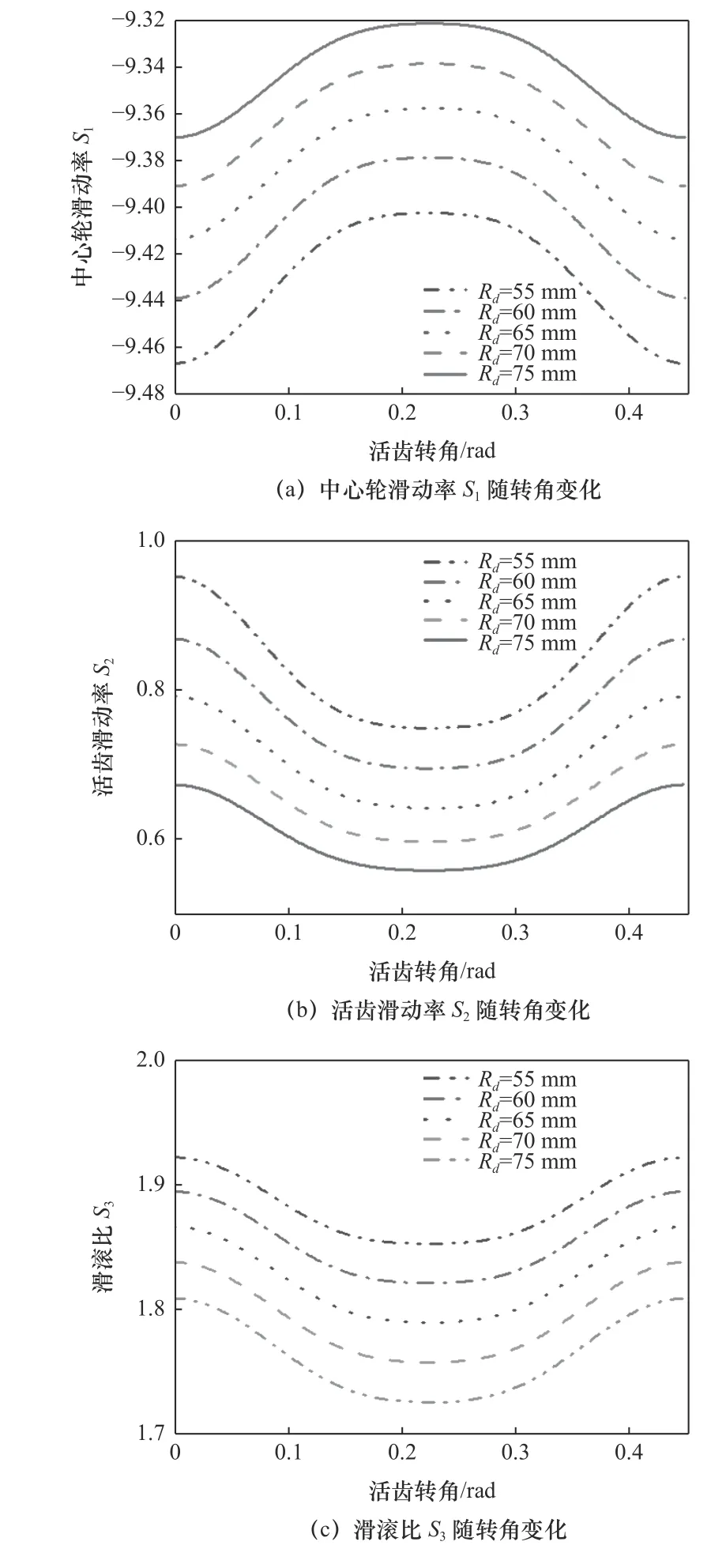
图4 激波器半径对滑动率和滑滚比的影响
由图4c可知,随着活齿转角θG从0增加到0.448 7 rad,滑滚比S3先减小后增大,在啮合点处滑滚比的变化率最大,在齿顶处变化率最小,滑滚比的峰值出现在中心轮的齿根处,激波器半径每增加5 mm,滑滚比峰值减小约1.62%。
在保证其他参数不变时,研究滚柱活齿半径r对滚柱活齿传动的滑动率和滑滚比影响,将滚柱活齿半径从4 mm增加到8 mm,每次增加1 mm,得到滚柱活齿半径对滑动率和滑动比的影响如图5所示。
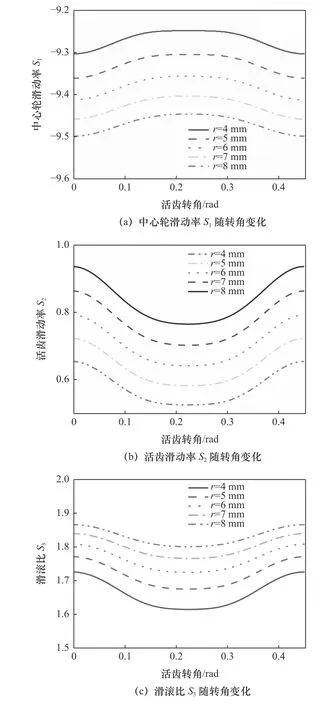
图5 滚柱活齿半径r对滑动率和滑动比的影响
由图5a和5b可知,随着活齿转角θG从0到0.448 7 rad,中心轮滑动率S1先增大后减小,滑动率变化率较小。随着滚柱活齿半径的增大中心轮滑动率峰值减小,在齿顶处达到峰值,每增大1 mm,峰值减小约0.54%。活齿滑动率S2正好相反,随着活齿转角θG增加,活齿滑动率S2先减小后增大,滑动率变化率较大,随着活齿半径的增大,活齿滑动率峰值增大,每增大1 mm,峰值增大约10.3%。
由图5c可知,随着活齿转角θG从0增加到0.448 7 rad,滑滚比S3先减小后增大,滑滚比变化率在啮合点处最大,在齿顶处滑动率变化率最小。随着滚柱活齿半径的增大,滑滚比峰值增大,增大的速度越来越慢。
当保证其他参数不变时,研究偏心距e从2 mm增加到4 mm,每次增加0.5 mm对滚柱活齿传动的滑动率和滑动比的影响,如图6所示。
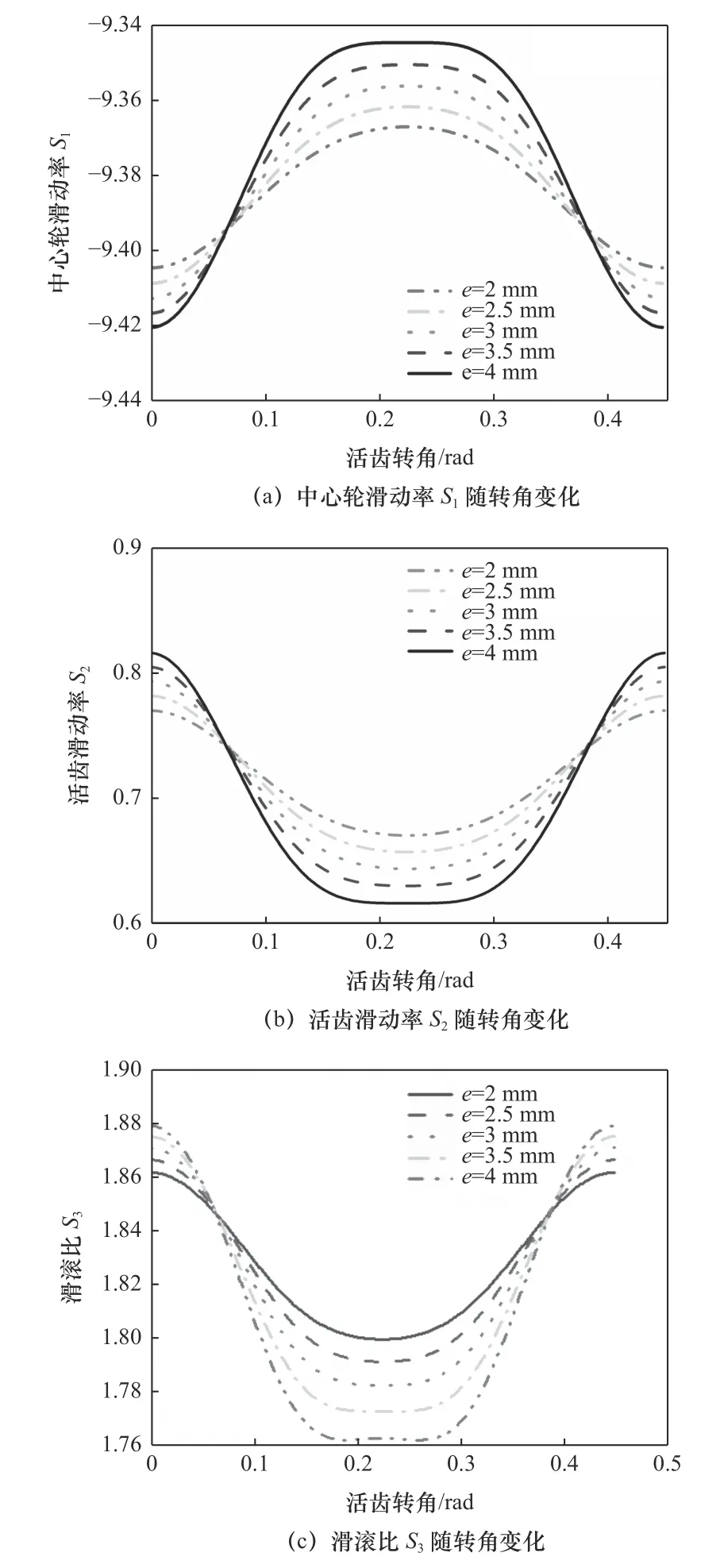
图6 偏心距e对滑动率和滑滚比的影响
由图6a和6b可知,随着活齿转角θG从0到0.448 7 rad,中心轮滑动率S1先增大后减小,滑动率变化率较小,活齿滑动率S2先减小后增大,滑动率变化率较大。随着偏心距的增加,中心轮滑动率峰值增大,每增加0.5 mm,中心轮滑动率峰值增大约0.005,在齿顶处达到峰值。相反,随着偏心距的增大,活齿滑动率减小,每增大0.5 mm,活齿滑动率峰值减小约0.011,在齿根处达到峰值。在拐点处,无论偏心距怎样变化,中心轮滑动率和活齿滑动率都不改变,而且在拐点后滑动率的变化趋势越来越大。
由图6c可知,随着活齿转角θG从0增大到0.448 7 rad,滑滚比S3先减小后增大,在啮合点处,无论偏心距变大还是变小,滑滚比S3都是保持不变的。随着偏心距的增大,滑滚比S3的变化率越来越大,在齿根处滑滚比达到最大值,在齿顶处达到最小值。滑滚比的峰值随着偏心距每增大0.5 mm,相应增大约0.004。
当保证其他参数不变时,研究传动比i从12到16,每次增加1,对滚柱活齿传动滑动率和滑动比的影响。因为传动比不同会导致滚柱活齿从齿根到齿顶再到齿根的活齿公转角范围发生改变,表2为不同传动比对应的滚柱活齿公转角。

表2 滚柱活齿公转角
由图7a、b可知,随着活齿转角θG增大,在对应的滚柱活齿公转角范围内,中心轮滑动率S1先增大后减小,滑动率变化率较小,在齿顶处滑动率达到最大值;活齿滑动率S2先减小增大,滑动率变化率较大,在齿根处活齿滑动率达到最大值。随着传动比增加,滚柱活齿在一个工作行程中公转角范围减少,中心轮活齿滑动率减小,并且减小的趋势变得缓慢;随着传动比增大,活齿滑动率增大,增大的速度保持恒定。
由图7c可知,随着活齿转角θG增大,滑滚比S3先减小后增大,在齿根处滑滚比达到最大值,在齿顶处滑滚比达到最小值;滑滚比变化率在啮合点处最大,在齿顶处最小。随着传动比的增大,滑滚比增大,滑滚比增大的速度变得越来越缓慢。
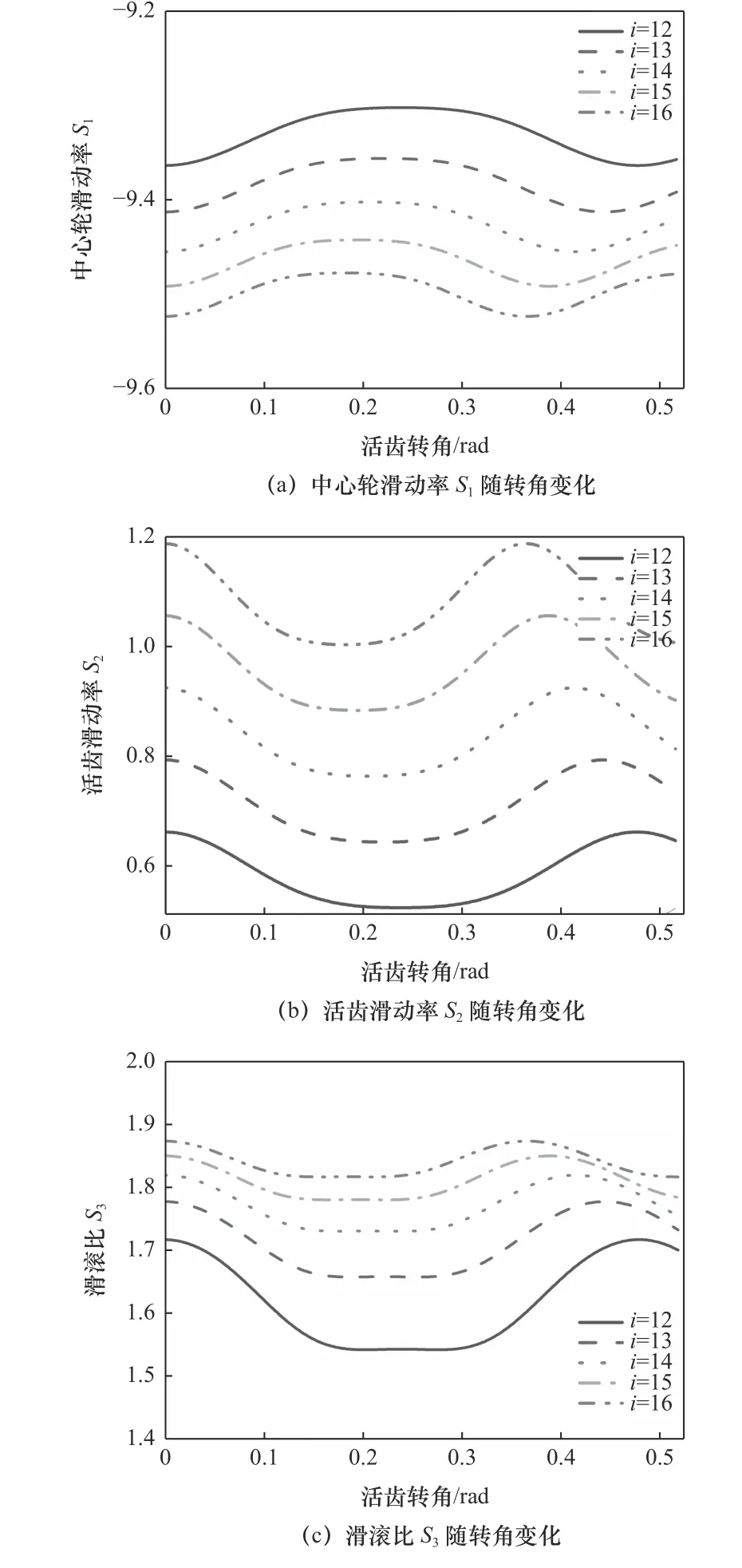
图7 传动比i对滑动率和滑滚比的影响
4 结语
本文基于滚柱活齿传动的结构特点和工作原理,建立了滚柱活齿传动的运动学模型,基于运动学原理,提出了滚柱活齿传动滑动模型,利用数值分析建模的方法分析了设计参数的变化对滑动率和滑动比的影响。研究结果可以为设计滚柱活齿传动结构参数提供依据,降低滑动率和滑滚比,减少传动摩擦,提高传动效率。
(1)中心轮滑动率S1和活齿滑动率S2的绝对值和滑滚比S3随着活齿转角θG增大先减小后增大,在啮合点处,滑动率和滑滚比的变化率最大,在齿顶处变化率最小。
(2)随着激波器半径Rd和偏心距e增大,中心轮滑动率S1增大,活齿滑动率S2和滑动比S3减小;当滚柱活齿半径r和传动比i增大时,中心轮滑动率S1减小,活齿滑动率S2和滑滚比S3增大。
(3)滚柱活齿半径r对活齿滑动率影响较大,随着活齿半径增大,每增大1 mm,活齿滑动率峰值增大约10.3%。偏心距e对滑动率和滑滚比变化率的影响较大,在啮合点处无论偏心距怎样变化,滑动率和滑滚比保持不变,并且过了啮合点偏心距越大,滑动率和滑滚比的变化率越快。
