基于主成分回归法的Johnson-Coo k损伤准则的渐进成形破裂预测*
2023-02-24王佰超许虎张澧桐张洪明王慧冬
王佰超 许虎 张澧桐 张洪明 王慧冬
(①长春理工大学机电工程学院,吉林 长春 130022;②内蒙古第一机械集团股份有限公司,内蒙古 包头 014000)
板材渐进成形工艺[1](以下简称渐进成形工艺)作为一种柔性无模板材成形新技术,成形轨迹可以提前编写,采用“分层制造”想法,对模具没有依赖性,复杂曲面零件也可以通过渐进成形进行加工。柔性板材渐进成形工艺类似于3D打印,均为复杂三维模型在高度方向离散并分解为一系列二维断层面,分层进行加工,最终实现目标形状的制造。渐进成形的另外一个特点是柔性化,成形轨迹可预先编制,可方便实现成形形状的改变,使成形工艺更加灵活。另外,成形过程易于实现是自动化甚至智能化,可有效融合在线监测技术实现成形质量的闭环控制。渐进成形因其灵活性高,开发时间短,经济成本低等特点,在多品种、小批量生产中具有巨大优势。图1为渐进成形原理图。
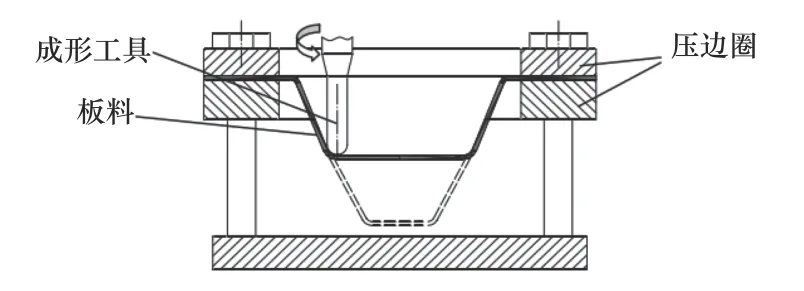
图1 渐进成形原理图
金属板材渐进成形作为一种先进的加工工艺,加工中难免出现一些不可避免的缺陷:零件成形失效,过度减薄或者发生破裂;成形件表面质量欠佳,如大尺度波纹度和材料沉积;零件几何精度低,如回弹、下沉等现象[2-3]。
破裂是指在渐进成形过程中随着板材表面积的增大,厚度不断减薄直至不能承受成形力的现象。这是因为在单点工具头的加工过程中,工具头与板材的接触类似于逐点接触,板材上与工具头接触的点应力集中明显,其中包括两向拉应力和一向压应力,尤其在垂直进给位置时还受到很大的冲击载荷,因此在板材加工的后期很容易产生破裂缺陷。如图2为成形角为71°时板料破裂图,破裂高度为-12.84 mm。针对板材成形发生破裂的处理手段,可以根据以下两个层面上解决:

图2 板料破裂图
(1)降低刀具在加工过程中,板材成形区的进给量,尽量在0.1~2 mm。
(2)板材应选取塑性能力强,比如抗拉强度,屈服强度都要比一般材料要高;延展性好的材料,可以扩大所需变形区,从而减少成形力的集中。
戴聪聪[4]以韧性值为评价指标,得出了双点渐进成形工艺参数对板材破裂的影响规律,得出以下结论:成形角影响最大,其次为板厚、刀具直径和进给量,进给速度影响最小。不过试验数据较少,不能完全证实该结论的成立。利用Oyane断裂准则,杨琴[5]根据应变率效应,计算出铝合金材料在破裂过程中的材料参数并且总结出应用于渐进成形铝合金材料的破裂准则。但提出的韧性破裂准则仅对圆锥台进行了应用,对于大型复杂零件需要进一步研究。朱浩[6]通过对铝合金在剪切力作用下的断裂行为及力学性能进行研究,发现随着剪切应力速率的增加,剪切断裂应变会降低。而剪切应变速率对铝合金的剪切强度几乎没有影响。同时,还得出结论,在剪切应力的作用下,微裂纹的产生和扩大基本上是完成的。但是未针对车用铝合金进行撞击等实验,仅仅通过拉伸试验和有限元模拟来确定铝合金的损伤和断裂机制。李军超等[7]在数值模拟过程中,采用了均匀分布策略和正反转交替的处理方法,有效地避免了G代码处理轨迹导致的板料断裂等不稳定现象。但对摩擦机理的研究不够深入,需要找到更好的润滑方法。Maria B Silva[8-9]等讨论了单点渐进成形过程中刀具头直径等工艺参数对AA1050-H111铝板成形极限和断裂的影响。此外,对单点渐进成形过程中颈缩现象的发生也作了进一步说明。比较了单点和双点渐进零件成形精度和成形的其他性能。但是研究对象主要是方锥台和圆锥台件等之类的简单轴对称制件,需要对复杂异形件进行更多研究。Duc Toan Nguyen[10]等结合混合硬化法则和Oyane[11]韧性断裂准则利用有限元仿真寻找到了在对镁合金材料的韧性断裂影响因子中,刀具半径和进给量的增大,板料的成形极限也随着降低,两者成反比,成形极限预测结果却以混合硬化法则较为精确。但是数值模拟的过程复杂,时间过长,需要开发一套适用于板材多点复合渐进成形的专用软件。
1 主成分分析回归原理与步骤
1.1 主成分分析回归法的原理
主成分分析[12](principal component analysis)是多元统计分析的重要降维和分析评价方法;多元分析(multivariate analyses)作为一种多变量统计分析方法在数理统计领域有着广泛应用。它主要使用所有的自变量运行主成分分析,对自变量进行降维,获得一组互不相关(正交)的主成分,这些主成分承载了原始变量的方差。所以在建立线性回归方程时无需考虑各个参数之间的交互作用,它的建立是依靠矩阵相同参数对应方程的参数,因此不会出现参数相乘或者平方的情况。
主成分分析(PCA)的要旨是主成份分析的目的是用尽量少的主成份代表众多的变量,因此它们所包含的信息量不应该损失太多。应用这一原理可以从大量数据(如温度、湿度等)中提取出与之相关程度高的信息,从而达到简化数据处理过程和提高预测精度的目的。用这种方法进行了预报试验。这说明主成分分析其实就是降维方法之一。
1.2 主成分分析回归法的步骤
(1)对原始数据建立矩阵,将原始数据标准化,假定主成分分析指标变量假定主成分分析指标变量(渐进成形样品)有n个,每个指标变量都有P个主要影响因子,将原始数据转化成xnp的矩阵,见式(1)。
(2)标准化处理。
对于各个因素的单位的不同,需进行统一处理,所以将各个因素指标进行标准化,如式(2)。
(3)计算相关系数矩阵,如式(3)。
式中:rii=1,rij=rji,rij就是第i项指标和第j项指标之间的相关系数,见式(4)。
(4)计算特征值与特征向量。
①计算相关系数矩阵的特征值 λ1≥λ2≥···≥λP≥0。
②计算出对应特征值的特征向量u1,u2,···,uP。
(5)主成分指标的确定。计算特征值λi(i=1,2,···,p)的信息贡献率及累积贡献率。
(6)线性回归方程的建立。已知主成分指标变量条件下,将以上主成分指标设出线性回归,见式(5)。
根据式(5)计算出包含Z1,Z2,···,Zm的线性回归方程,代入主成分式子,可得出关于X1,X2,X3,···,Xp的线性回归方程如式(6)。
1.3 Johnson-Cook本构模型
Johnson-Cook本构模型[13]可以描述金属在变形量大,应变速率高,温度高的条件下的塑性变形行为。该本构模型定义的等效断裂应力为:
式(7)显示了金属的流变应力与应变、应变速率和温度之间的关系。其中:σ为非零应变率时金属的屈服应力;A为初始屈服应力;B为硬化常数;ε为等效塑性应变;n为硬化指数;C为应变率常数;ε˙ 为应变速率;T*为对同系温度;m为热软化指数。
Johnson-Cook本构模型可以与渐进性损伤和失效模型联合使用,来指定不同的损伤初始准则和损伤演化规律,来允许材料刚度渐进退化并从网格中去除单元,即可以显示出破裂的现象。
1.4 Johnson-Cook损伤准则
Johnson-Cook损伤准则[14]是韧性准则的特殊情况。Johson G.R等[15]提出一种动态失效模型(Johson-Cook本构模型),它以单元积分点等效塑性应变值为依据而创建出来的。假定相关性是分离的并具有以下形式:
式中:σ*=p/σeff=-σm/σeff=-Rσ,p为压应力,σeff为Mises应力,Rσ为应力三轴度;ε˙*=ε˙/ε˙0,ε˙是塑性应变率,ε˙0为参考应变率,通常为 1s-1;T*是无量纲温度;D1~D5是在转变温度或其之下测得的失效参数。因为大部分材料随着压力与偏压力之比的增加,其 εf增加,所以上述表达式的D3通常采用正值。
Johnson-Cook动态失效模型是具有硬化规律和率相关分析形式的Mises塑性模型的一个特殊种类。它适用于许多材料,包括绝大部分金属的高应变率变形。同时可以在Abaqus/Explicit中与Johnson-Cook动态失效模型联合使用。而且Johnson-Cook动态失效模型提供两种失效选择,包括作为结构撕裂或剥开的结果从网格中去除单元。渐进性损伤模型允许材料刚度的平滑退化,以使得它们适用于准静态和动态两种情况,这对于研究渐进成形的板材破裂是极大的优势。
2 材料参数和实验研究
2.1 铝合金材料参数
本实验选用6061AL,铝合金属于可加工性好、焊接性、成形塑性和屈服强度的热处理强化合金。退火后仍能保持一定的可操作性,表1是其材料参 数。

表1 6061AL材料参数
由朱浩等人的实验结果知AL6061的Johnson-Cook本构模型为:A=250MPa,B=265.94 MPa,n=0.32,C=0.002,m=0,D1=0.299,D2=1.496 5,D3=3.32,D4=D5=0。
2.2 正交实验设计
本文选用刀具直径、层间距、成形角、板料厚度、成形高度和制件尺寸作为6个试验因素,每个因素选取3个水平如表2所示,选取破裂高度目标参数,设计6因素3水平的L18(36)正交试验,其试验方案及结果如表3所示,图3为板料加工的工艺参 数示意图。
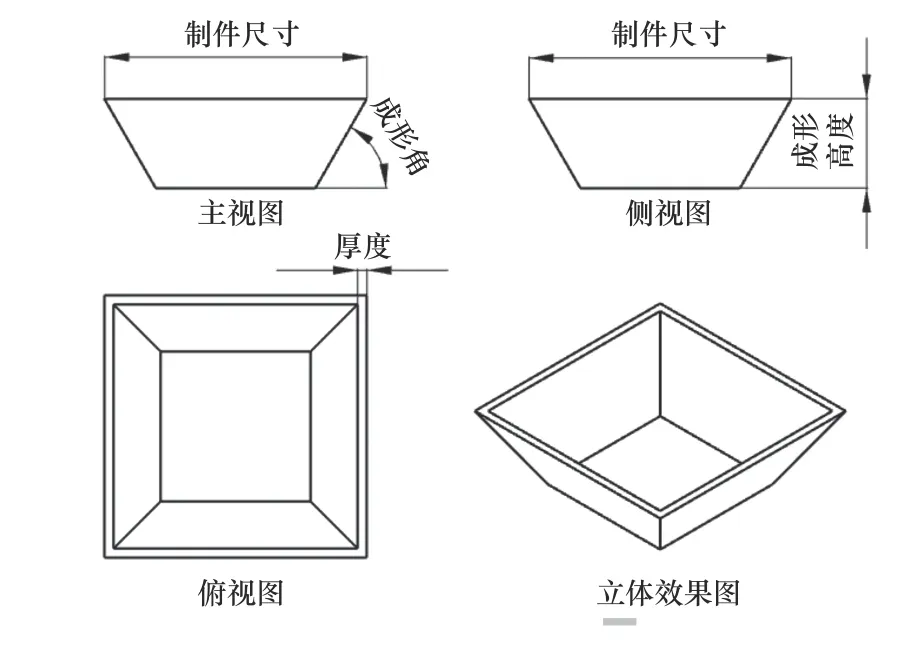
图3 工艺参数示意图
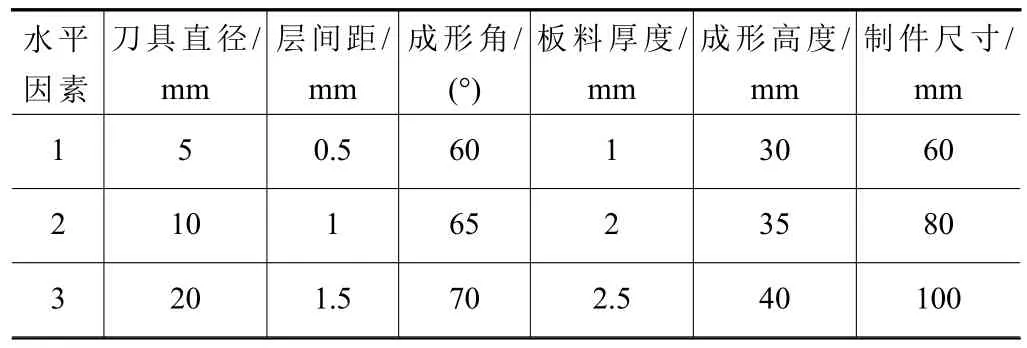
表2 渐进成形试验因素水平表
2.3 渐进成形实验设备
渐进成形设备是实现渐进成形过程的关键,由于渐进成形力相对于传统冲压成形所需的成形力要小很多,这样就使得该类工艺的成形设备比较小巧,而且容易自主研发制造。本文采用自主研发的渐进成形设备来
对本课题进行研究,该设备为CNC六自由度数控渐进成形设备,该机床在工作时,工作台不会移动,以并联机构的运动来实现在XYZ方向的运动,各轴运动指令主要靠计算机数控加工模拟软件传输数控加工代码来实现,具体如图4所示。

图4 渐进成形实验设备
3 主回归方程的建立
在渐进成形过程中,板料的破裂时常发生,而影响破裂的因素有很多,例如:刀具直径、层间距、成形角、板料厚度、板料材质、刀具运动轨迹、成形高度、刀具转速和制件尺寸等。选取6个关键工艺参数因素来探索板材破裂深度:刀具直径、层间距、成形角、板料厚度、成形高度和制件尺寸。表3为板材破裂的影响因素表。
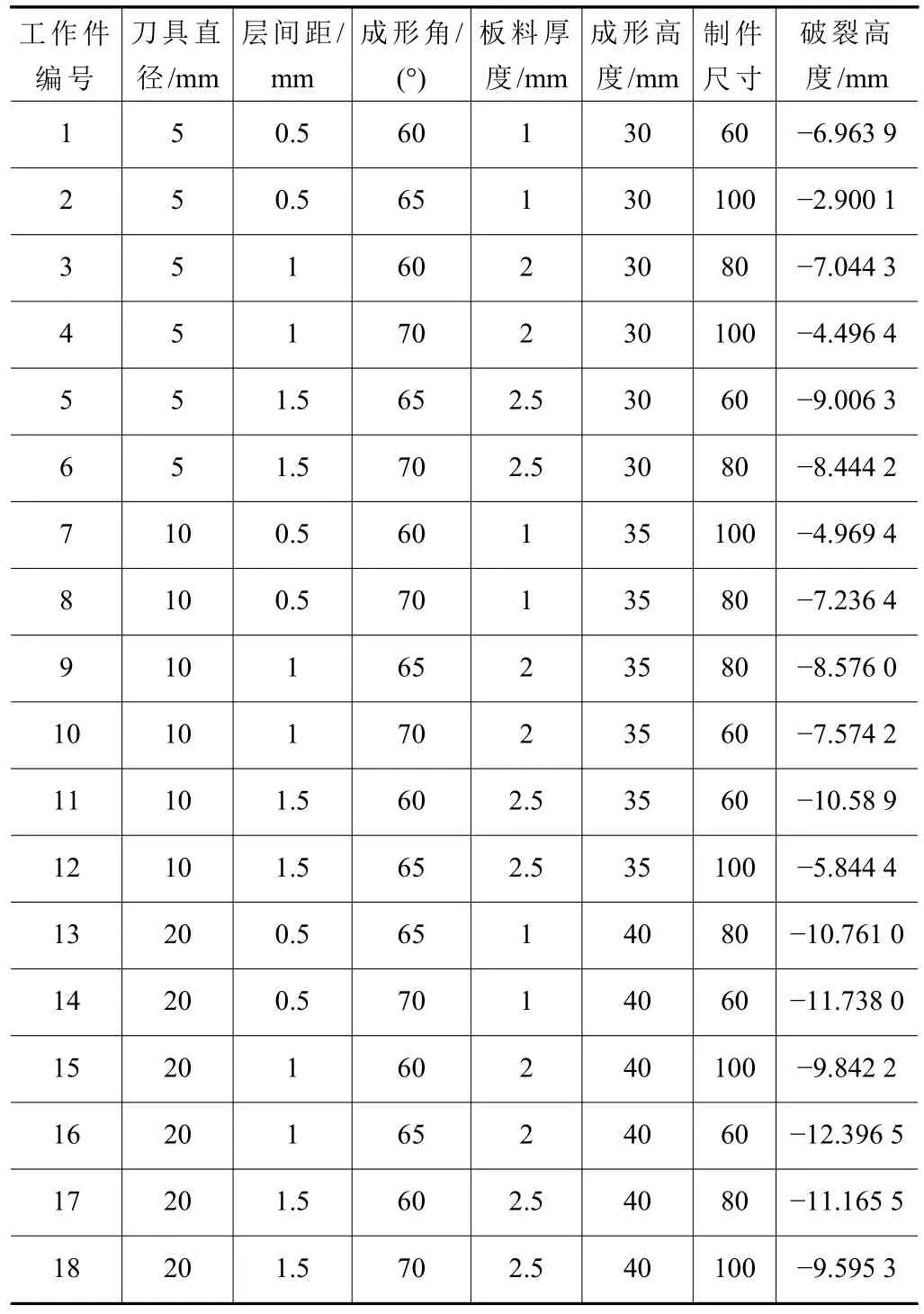
表3 板料破裂的影响因素表
3.1 建立主回归方程
对于上述18个工作件所选取的6个指标分别依次确定为x1~x6,将赋予数据的矩阵进行标准化处理。为了验证主成分回归法对预测板料破裂高度具有可靠性,将前16个工作件的数据作为分析数据,将后17和18两个工作件数据作为方程结果的证明。设x1~x6构成的矩阵为矩阵A,如公式(10)。
第一步:使用SPSS统计学软件对式(10)作标准化处理,获得标准化矩阵B,如式(11)。设~(矩阵B)为标准化处理的6个指标。
第三步:再次运用SPSS数据分析软件对相关系数矩阵C进行特征向量与特征值计算,设该矩阵为矩阵D,如式(13)。
第四步:确定主成分,如式(14)。
基于已知特征向量及特征值,计算主成分贡献率及累计贡献率,如表4。
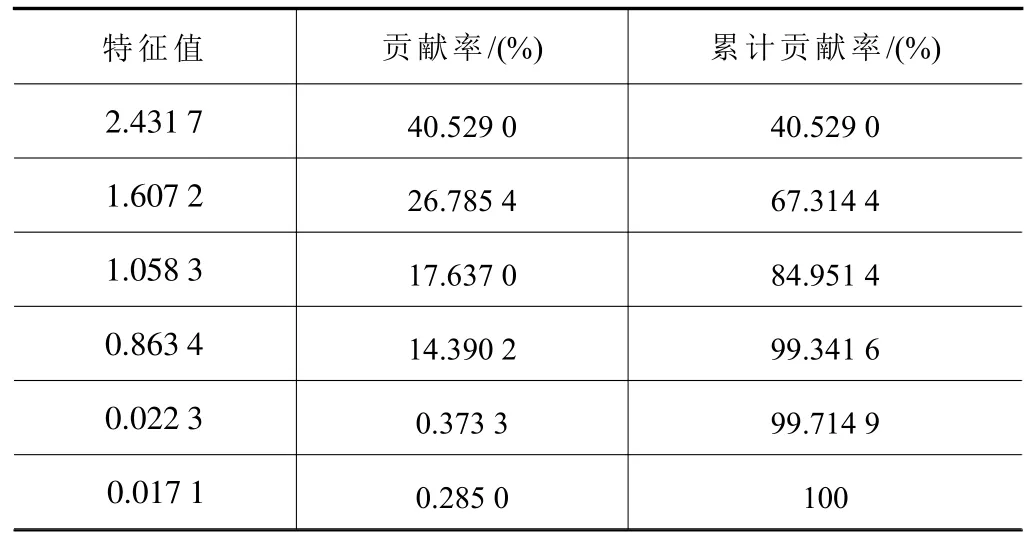
表4 主成分特征值和贡献率
观察表4可知,前4个主成分F1~F4特征值的累计贡献率超过85%,达到99.341 6%,由上文可知,主成分分析的成立的标准(累计贡献率>85%)已满足,取这4个主成分,建立线性组合如式(15)。
根据式(15),通过判断主成分对应的变量系数的绝对值的大小对比,来决定工艺参数因素对板材破裂高度的影响重要性。由此可知,x1、x2、x4和x5可以被看作F1的变量,即反映了刀具直径,层间距,板料厚度和成形高度对板料破裂高度的影响;同理,x3可以被看作F3的变量,体现出成形角对板料破裂高度的影响;而制件尺寸对板料破裂高度的影响则需要通过观察x6。表5为F1、F2、F3和F4的得分。取前4个主成分建立回归方程(式(16))。
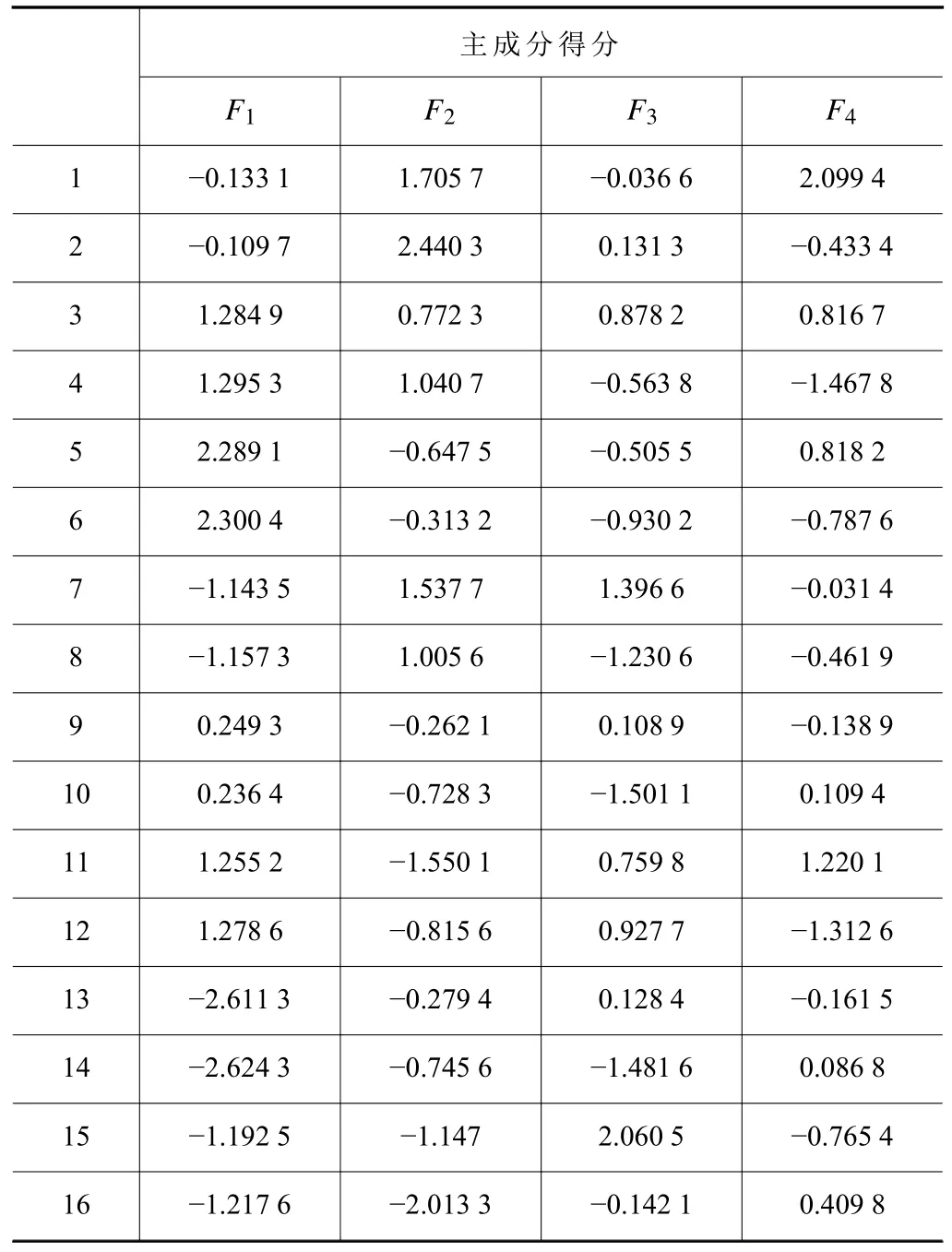
表5 主成分分布表
采用最小二乘估计可得式(17)。
将式(15)数据代入式(17)可得到式(18),式(18)即为原自变量的回归方程系数;再把标准化之后的数据转换成初始数据,表6为初始数据的回归方程系数。解得线性回归方程式如式(19)。
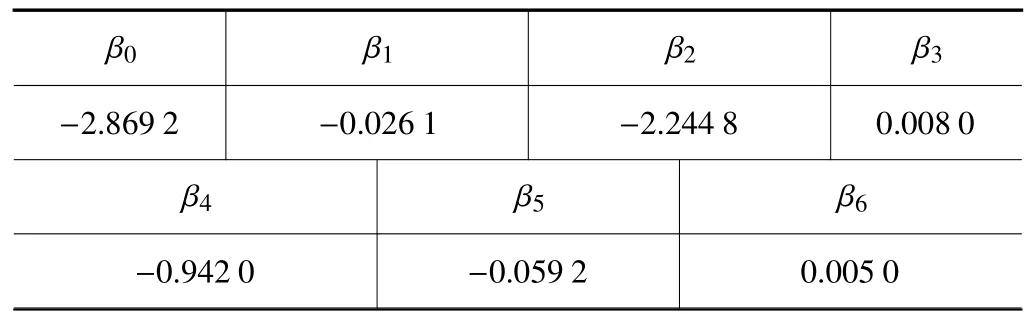
表6 原始数据回归系数
3.2 回归模型检验分析
3.2.1 回归显著性检验
假设H0线性关系不显著,根据公式(20)计算出统计量F,将回归离差平方和(SSR)和剩余离差平方和(SSE)进行比较,见式(20);确定显著性水平α,再通过分子1和分母n-2的自由度找出临界值Fα,最后判断F与Fα的大小,如果F>Fα,则拒绝H0,反之接受H0。
根据步骤确定α=0.05,检验统计量F可通过MATLAB软件计算出为42.453 8,则F>Fα(拒绝假设H0),表示回归方程显著且回归模型成立。
3.2.2 回归系数显著性检验
提出假设H0:β1=0(没有线性关系)或者H0:β1≠0(有线性关系);接着计算检验的统计量t如式(21)。最后根据显著性水平α判断 |t|与tα/2的大小,如果|t|>tα/2,表示拒绝H0,反之表示接受H0。
由上述检验可知α=0.05,用MATLAB数据分析软件得到的xi对y的线性作用结果见表7。由表7可知,显著性都是0,因此xi对y的线性作用具有显著性且成立。

表7 xi对y的线性作用
4 渐进成形破裂高度
4.1 主成分分析回归模型
根据以上回归模型的检验分析,已经确定了回归方程模型的准确性。将最后需要验证工作件17与18的刀具(直径)和板料(成形角、成形高度、厚度、制件尺寸、层间距)的量化指标代入回归方程,可以得到预测的板料破裂高度,将其与实际值相对比,相对误差见表8。
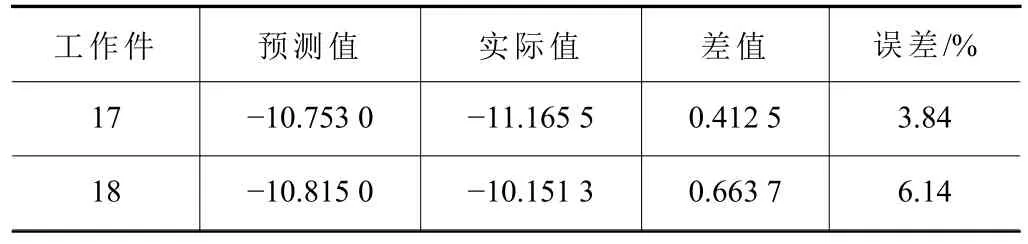
表8 实测值与预测值对比
4.2 线性回归对比
针对式(19)的验证,采取另一种方式:利用Minitab求出线性回归方程进行对比。将16组数据导入Minitab并回归分析中使用逐步法可算出式(22)。
再将工作件17和18的参数代入可计算得到破裂值分别为-5.390 4 mm和1.352 7 mm。可以看出该方程不符合此实际破裂值,并且方程中舍弃了成形角和板厚这两个参数,故利用主成分回归分析更符合实际。
4.3 结果分析
主成分分析的要领在于从数据中抽提到的主成份相当于对于数据的一种浓缩,得到的主成份往往综合了多个变量的信息,因此可以用于进行综合评价。破裂高度为板材破裂最低处和板材起始位置的距离。经过测量,得到工作件17与工作件18的破裂高度分别为-11.165 5 mm与-10.151 3 mm,其应力图结果如图5所示,图6则显示为两工作件的破裂高度。又根据式(19)可计算出两工作件预测的破裂高度分别为-10.753 0 mm和-10.815 0 mm,预测相对误差都是10%之内,分别为3.84%和6.14%。与Minitab回归分析的预测结果相对比,采用主成分回归分析模型方法对工件的破裂高度具有更高精度的预测,可以更好地预测板材的破裂高度。

图5 工作件17(左)和工作件18(右)破裂应力图
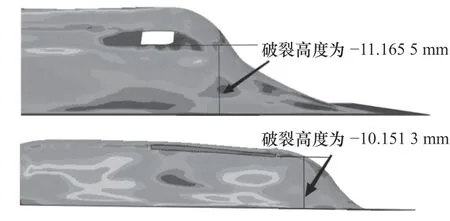
图6 工作件17(上)和工作件18(下)破裂图
5 结语
(1)本文使用ABAQUS仿真软件针对铝合金材料破裂的预测,采用Johnson-Cook本构模型与Johnson-Cook损伤准则,可以很好地描述铝合金的失效应变,应用于渐进成形破裂仿真中是可行的。
(2)影响渐进成形板材破裂高度的工艺参数共6个,采用主成分分析的方法,选择了前4个主成分分量用于回归分析预测。它不但可以提高结果质量和准确度;还能使评价过程更简洁、合理;同时也可避免人为主观因素造成的偏差,减少指标选择的工作量,从而得到更好的效果。
(3)通过实测数据可知工作件17与工作件18的破裂高度分别为-11.165 5 mm与-10.151 3 mm,基于16个工作件的实测数据建立的主成分回归模型,对两工作件破裂高度预测分别为-10.753 0 mm和-10.815 0 mm,预测相对误差分别为3.84%和6.14%。
