基于电子齿轮箱的展成磨齿多轴同步自适应控制*
2023-02-24韩江周广鑫夏链黄晓勇李彦青田晓青
韩江 周广鑫 夏链 黄晓勇 李彦青 田晓青
(①合肥工业大学机械工程学院,安徽 合肥 230009;②安徽省智能数控技术及装备工程实验室,安徽 合肥 230009)
展成磨齿是齿轮一种常见的主要精加工手段,数控磨齿实际加工中,其运动参数、受力状态、热变形以及转矩实时变化,使得工件在进行磨削时出现形位偏差以及磨齿机床运动偏差明显增加。磨齿高速高精度加工对多轴控制精度提出更高的要求,研究利用电子齿轮箱(EGB)进行磨齿机多轴控制就显得尤为重要。在展成磨齿过程中,工件回转轴、刀具回转轴和各进给轴按照电子齿轮箱约束关系进行联动,共同完成齿轮的磨削加工,但是由于整个运动系统出现的响应延迟、加工过程中产生扰动、传动丝杆自身制造误差等导致磨齿机床各轴无法按照啮合规则同时完成理想动作,这是产生齿轮加工误差的主要原因[1]。采用合适的控制策略保障多轴联动精度,补偿系统的控制误差,对于提高实际工况齿轮加工具有重要意义。
在高速磨齿时,磨削力实时波动,使得主轴转速跟踪误差变大问题逐渐凸显,目前主要研究方法包括建立转速跟踪误差与齿形误差之间的数学模型方法、磨削加工中的插补控制以及误差补偿等[2]。上述方法对于提高系统控制精度有一定参考价值,但展成磨齿在高速高精度工况下,由于多轴联动延迟、扰动等因素,减小单轴跟踪误差并不能保证整体控制精度,各运动轴并未至理想位置。针对多轴同步运动控制问题,Sarachik P等人[3]提出交叉耦合(CCC)概念,使用计算产生的同步误差逐步调整被控轴达到同步运动。Koren Y等人[4]对交叉耦合模型进行完善,首次实现了在数控系统中的应用。田晓青等人[5]提出了一种将软件式电子齿轮箱与交叉耦合控制策略相结合电子齿轮箱交叉耦合控制器(ECCC),结果显示交叉耦合控制模型取得了较好的控制效果,能够迅速、实时消除工况中的扰动,但为了得到合适的反馈信号,计算各轴轨迹轮廓误差仍是难点。为了降低控制难度,简化计算模型,学者们采用多种控制方法相结合来实现多轴之间高性能同步控制。其中包括PID控制、鲁棒控制、最优化控制和干扰观测器等[6-7]。彭晓燕等人[8]提出一种适用多个电机同步PI补偿控制的改进型偏差耦合控制结构,仿真结果说明,该结构具有更高同步精度。Jeong S K等人[9]提出了一种多轴回转系统同步位置控制方法,保证鲁棒性同时,使用最大误差比较法减少各轴之间同步误差,仿真与实验表明可有效提高控制精度。为了解决实际工况系统性能参数的实时波动,干扰观测器和自适应控制是学者们主要选择的控制方法,徐壮等人[10]比较了滑模观测器与卡尔曼观测器之间的特点,研究表明卡尔曼观测器对外界噪声等干扰更加敏感,位置感知更加优秀,适合高速高精度的场合。
磨齿加工精度由机床同步精度直接决定,常见能够有效确保同步精度策略包括交叉耦合、最优化控制、模糊控制与神经网络、干扰观测器等,通过对磨齿工艺分析,针对实际工况中时变扰动特点,选择干扰观测器中的扩展卡尔曼观测器作为该系统的控制策略。本文针对磨齿工况中磨削力等扰动引起的同步精度问题,建立了一种基于电子齿轮箱的多轴联动模型,给出加工齿轮误差与工件轴误差之间的数学关系,设计了一种针对实际工况磨削力波动具有自适应功能的扩展卡尔曼观测器,将磨削力波动作为扰动参数输入系统,对多轴联动过程产生的磨削力进行观测,并使用设计并验证的前馈模型对其磨削力产生的位置误差进行补偿,大幅度降低系统控制误差,通过实验验证本方法的有效性。
1 磨齿原理与电子齿轮箱结构
1.1 磨齿加工运动原理
蜗杆砂轮磨齿加工原理及运动关系如图1所示。实现磨齿运动包括:砂轮回转运动B轴、工件回转运动C轴、轴向进给运动Z轴、切向进给运动Y轴、径向进给运动X轴与刀架回转运动A轴。其中各进给轴控制磨削进给量,刀架回转A轴控制刀具安装角度。

图1 蜗杆砂轮磨齿加工原理及运动关系
1.2 磨齿加工数学模型
根据蜗杆砂轮磨齿原理,加工过程中,砂轮和工件在电子齿轮箱控制下,按照一定速比关系实现展成磨削运动,刀具沿着工件轴线方向进行进给完成齿面磨削,为了磨削加工效果,在磨削量和加工速度较大时,需要砂轮沿自身轴线(Y轴)作窜刀运动。整个加工过程,被加工齿轮不仅需要与蜗杆砂轮保持一定啮合关系,还必须和刀具进给运动保持一定约束关系。
在磨齿过程中,砂轮和工件之间相互运动遵循啮合原理,C轴跟随Z轴产生的转动为[11]
C轴跟随Y轴产生的转动为
则工件回转C轴与其他各轴的联动关系为
式中:k为砂轮头数;z为齿轮齿数;λ为砂轮安装角;β为工件齿轮螺旋角;mn为齿轮法面模数;Ki(i=b、z、y)为各轴方向系数,取值为“1”或“-1”;Δi(i=Z、Y)为i轴跟踪误差,Δnic(i=z、y、b)为i轴附加在C轴上的转动。
1.3 电子齿轮箱控制系统结构设计
在磨齿中,设计电子齿轮箱结构如图2所示。
电子齿轮箱结构模型采用主从式和平行式相结合的结构模型,其中刀具主轴采用速度控制模式,各主动轴输入插补信息经过相应的模块后由编码器反馈至电子齿轮箱模块进行保存,在电子齿轮箱中根据各轴间展成关系运算后得到工件轴输入插补信息,从而加工出符合要求的齿轮。由于电子齿轮箱使用主切削轴实际反馈位置对从运动轴进行控制,从运动必然相对主运动存在滞后,而系统各轴又为独立控制,各轴同步精度取决于各轴对插补指令的跟踪精度,为了进一步提升电子齿轮箱控制精度,必须要设计控制策略对其进行优化。
1.4 电子齿轮箱控制误差模型
齿轮的加工精度直接由电子齿轮箱同步精度决定,当系统同步精度较差时,所加工齿轮存在严重误差,如图3所示,分别对齿形和齿向造成不同程度误差,严重影响齿轮精度。为了提高系统同步精度,减小电子齿轮箱控制误差,需研究系统控制误差与齿轮加工误差之间的数学关系。

图3 齿轮加工误差示意图
由于齿廓偏差受螺旋角、刀具等综合影响,电子齿轮箱控制误差在加工齿轮过程中主要体现在齿轮齿距偏差和螺旋线偏差上,对于图2所示的电子齿轮箱结构,由于采用主从式结构跟随主轴运动,主轴跟踪误差不会对电子齿轮箱精度造成影响,根据加工过程中刀具与工件相对位姿关系,综合考虑安装角、螺旋角、X、Y、Z轴跟踪误差等,得到齿距偏差Fp的数学模型为[1]

图2 磨齿加工电子齿轮箱控制模型
综合考虑得到螺旋线偏差Fβ数学模型为
根据磨齿过程中实际多轴联动关系,综合式(3)、(4)、(5),得到齿距偏差和螺旋线偏差相对于工件转轴误差的表达式分别为
式中:z为加工齿轮的齿数;λ为砂轮安装角;β为工件齿轮螺旋角;mn为加工齿轮法面模数;Ki(i=b、z、y)为各轴方向系数;Kpi(i=c、y)、Kβi(i=c、y、z)为偏差方向系数,取“1”或“-1”;Ei(i=c、x、y)为i轴误差。
分析式(6)和式(7)可得,在磨齿多轴联动中,可以将各轴误差通过联动关系的方式累积到工件轴上,推导出电子齿轮箱控制误差与齿轮展成加工误差之间的映射关系,为加工过程中实时估算齿轮相关精度情况提供了可能。
为了能够准确地实时估算出电子齿轮箱控制精度,确保系统的鲁棒性,需要实时读取能够反应磨齿过程中受到的扰动,并利用该参数保障系统同步精度,设计了一款能够观测该参数的滤波观测器。
2 自适应卡尔曼观测器设计
2.1 观测器模型原理与设计
在磨齿工况中,作用在工件运动轴上时变的等效磨削力会在电机内部的电流中引入对应扰动,使得电机在运行过程中出现干扰信号,从而引起误差。为了探究工况中磨削力与电机最终输出误差之间的关系,设计补偿策略,搭建工件运动轴观测器如图4,输入信息为电子齿轮箱运算得到的插补,由传感器得到的电流iq和转速 ωc作为输入参数进入观测器中,观测器将观测得到的磨削力矩进行输出。电流环部分按照永磁同步电机的运行原理进行搭建。

图4 PMSM观测器-控制器结构框图
其中电机运动方程为
工件回转轴采用闭环控制,因为电磁时间常数远远小于机械时间常数,电流环稳态时间相对速度环可以忽略。测量转速和电流由传感器返回。
综上所述可以把电磁转矩和摩擦转矩引起的扰动全部等效为负载扰动。根据式(8)可得系统离散系统状态空间和测量方程分别为
式中:xk为二维状态向量;uk为输入电流iq;Ts为离散时间常数取0.1ms;Ke为电流系数;ϕ、B、H为状态空间的系数矩阵。
由于建模偏差和测量误差等问题,考虑动态噪声与测量噪声系统状态方程与测量方程修正为
式中:ωk和vk+1vk+1为系统模型扰动与测量误差。
由于卡尔曼观测器对外界噪声等干扰更加敏感,且在协方差矩阵合适情况下具有更高的观测精度,适合高速高精度场合。因此针对磨齿选择扩展卡尔曼观测器进行控制。扩展卡尔曼观测器可以使用相应的协方差矩阵对输出进行滤波,如图5所示,包括预测和修正过程两部分。其预测过程表达式为

图5 自适应卡尔曼观测器原理框图
修正过程表达式为:
为了能使得协方差矩阵Q能够根据扰动和突变进行自适应变化,建立k时刻协方差矩阵Qk为
2.2 前馈设计
为了运用改进观测器观测的磨削力,设计基于磨削力观测值运算的前馈补偿,需要建立以力矩形式反应在工件轴磨削力与加工工件偏差之间的数学关系。在Simulink中搭建工件轴仿真模型,通过前述研究将磨齿中磨削力进行叠加,得到反应在工件整体上的磨削力数据,选取该参数为模型扰动引入,观测模型输出位置量与引入扰动之间数学关系,基于此逻辑设计前馈补偿,来平衡扰动所带来的误差。结果如图6所示,输出位置加速度与引入扰动呈线性关系,选取适当比例系数k1积分补偿模型为

图6 输入磨削力与输出加速度示意图
其中:T为输入磨削力,a为输出加速度,可以据此对工况中实时变化的扰动进行补偿。
3 仿真及实验结果
为了验证设计系统的性能,在MATLAB Simulink环境下对其进行验证,并在基于DSP28335的多电机控制平台上进行试验,实验平台如图7所示,电机参数如表1所示。编码器线数为2 500 PPR,四倍频。系统工作频率10 kHz,电流环周期0.1 ms。

图7 多电机驱动控制实验平台
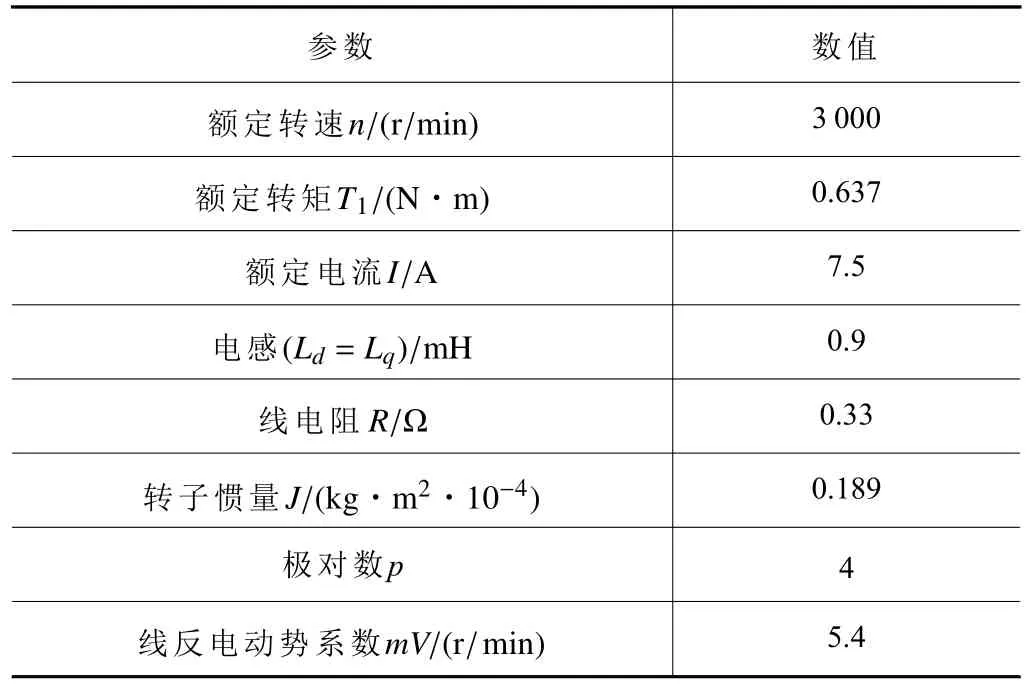
表1 电机参数
3.1 仿真结果分析
分别对观测性能以及补偿前后进行仿真试验,给定电机转速为60 r/min,接入扰动为前述磨削力参数,采样周期为0.1 ms。图8、图9为在仿真条件下,传统卡尔曼观测器和改进自适应观测器,对于引入模型输入磨削力和观测器观测到的磨削力之间的对比。由图中可以看出,在最开始极短时间受启动电流影响后,改进的自适应扩展卡尔曼观测器有效对电机产生的磨削力矩进行了观测,误差峰值不超过20 N ·cm,平均误差小于3 N ·cm,且观测系统整体滞后周期小于1 ms,可以得出其性能良好,观测值可靠性高。图10、图11为在仿真环境下,系统引入扰动后是否进行前馈补偿,加工齿轮螺旋线偏差和齿距偏差对比,可以看出,系统引入合适前馈,选择适当补偿系数k2,补偿后偏差值减小到扰动情况下1/5以内并且向0收敛,螺旋线平均偏差由26.32 μm降至3.77 μm,偏差幅值不超过7 μm;齿距平均偏差由41.63 μm降至6.92 μm,偏差幅值不超过11 μm。证明所建立的前馈补偿的有效性。

图8 传统观测器系统磨削力与观测磨削力对比图

图9 改进观测器系统磨削力与观测磨削力对比图
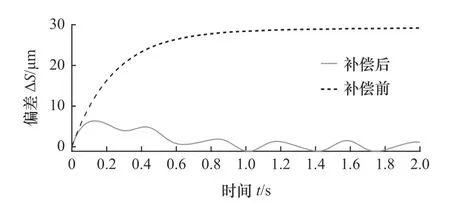
图10 补偿前后螺旋线偏差对比图

图11 补偿前后齿距偏差对比图
从仿真结果中可以看出,改进观测器和前馈补偿明显减少了加工工件的误差,提高系统的同步精度和鲁棒性,确保了磨齿工况中的抗扰动性。
3.2 实验结果分析
为了在实验中验证所设计的前馈补偿有效性,将前述磨削力参数作为负载输入到电机中,分别将系统在未加载、加载未补偿、加载带前馈补偿3种不同情况下对工件偏差进行对比,将转速控制在60 r/min情况下得到相应数据,通过实验平台反馈的偏差对前馈补偿进行检验。图12是在上述3种情况下由传感器和编码器所获得整个系统误差,可以看出,未加载系统本身由于静摩擦、粘性摩擦等,使得系统自初始即带有一定的误差。而在磨削力接入系统后,由于磨削力远远大于系统静摩擦等扰动,可以将其均等效到磨削力上,将其引入系统后对工件偏差产生了较大的波动,使得加工工件的精度受到巨大影响。在运用观测值运算出适合的前馈补偿并接入后,可以看出,由等效磨削力引起的工件偏差明显被所设计的前馈补偿平衡,在取样时间内,偏差幅值由488 μm降至13 μm,极差由591 μm降至13 μm。

图12 三种情况下偏差对比图
对比仿真与实验过程中出现的扰动与补偿效果,研究表明进行的仿真与试验有较好的吻合性,也说明仿真与试验的有效性。
综上所述,该前馈能够较好地吸收工况中出现的实时波动干扰并有效做出补偿,减小系统偏差,明显增加系统抗扰动性,鲁棒性大幅提高。
4 结语
通过研究电子齿轮箱控制模型与磨齿基本原理,基于齿轮螺旋线偏差、齿距偏差相对于同步等效工件运动轴偏差之间数学关系,结合扩展卡尔曼滤波算法,构建了具有自适应功能的观测器与前馈,实现了磨齿中动态扰动观测与补偿。为了贴近实际工况,引入的磨削力数据为工况下多齿受到的实时波动磨削力叠加的扰动。运用磨削力观测值,进行处理形成前馈对系统进行补偿,在高速高精度的环境下具有更好的控制效果。通过仿真和实验研究,所设计的观测器拥有较好的观测效果,可以准确地追踪工况中实时波动的扰动。结果表明,所设计的前馈补偿系统显著减小了加工工件的螺旋线偏差和齿距偏差,提升了系统的同步精度和抗扰动性。
