具有基数约束的多阶段均值-半方差可信性投资组合优化

2023-02-22崔淑琳李璟欣

运筹与管理 2023年12期

张鹏, 崔淑琳, 李璟欣

(华南师范大学经济与管理学院, 广东广州 510006)

0 引言

MARKOWITZ[1]提出了均值-方差投资组合选择模型。传统上,概率论是一个分析投资组合选择不确定性的主要工具。然而,如果没有足够的历史数据,假设风险资产的收益为模糊变量更合理。模糊投资组合选择已在许多文献中被提出,诸如VERCHER等[2],MOHEBBI和NAJAFI[3],JIN等[4]分别提出了几种多阶段模糊投资组合选择模型;LIU和ZHANG[5]提出了多阶段可能性投资组合优化模型。但以上模型中的可能性测度不满足自对偶性。为了弥补可能性理论的缺陷,LIU和LIU[6]提出了具有自对偶性的可信性理论。此后,学者们将可信性理论运用于投资组合研究中,如HUANG[7]构建了可信性均值-半方差投资组合模型。GUPTA等[8]探究了多阶段均值-半绝对偏差-偏度可信性投资组合选择模型。

现有的模型大多以Markowitz的均值-方差模型为框架,同时考虑一些现实约束,如基数约束和阈值约束。考虑交易成本,管理由大量资产组成的投资组合显然是不可取的。具有基数约束的Markowitz投资组合模型及其拓展模型在过去十几年里已被深入研究。特别是从计算的角度,一些研究者提出了精确解的方法,如BERTSIMAS和 SHIODA[9],LE THI和MOEINI[10]。由于精确解法只能够解决决策变量较少的情况,因此,许多学者提出了启发式算法求解,如LEUNG和WANG[11],YAMAN和DALKILIC[12]。事实上,标准Makowitz模型是凸二次规划问题,而具有基数约束的Markowitz模型是混合整数二次规划问题,属于NP完全问题。

现实生活中投资者可以将自己的财富在不同时期重新分配,因此,实际投资活动是动态且连续的。JIN等[4]构建了多阶段均值-方差-流动性投资组合模型;LIU和LIU[6]提出了多阶段均值-方差可信性投资组合模型。张鹏等[13]提出了多阶段均值-半方差随机投资组合模型。

本文引入了具有交易成本、借贷约束、交易量限制以及基数约束,构建了具有现实约束的多阶段均值-半方差可信性投资组合模型,并提出离散近似迭代算法求解。最后,用一个具体的算例验证了模型和算法的有效性。

1 预备知识

设ξ为隶属度函数μ的一个模糊变量,u和x是实数。对于任何给定的集合B(ξ∈B),可能性、必要性和可信性测度分别定义为:

其中可信性测度满足自对偶性,Cr{ξ≤r}+Cr{ξ≥r}=1。

定义1[6]设ξ是一个模糊变量。则ξ的期望值定义为:

(1)

定理1[6]设ξ和η是相互独立的模糊变量,λ和μ是两个实数。则

E(λξ+μη)=λE(ξ)+μE(η)

(2)

定义2[7]设ξ的期望值为e,(ξ-e)-=min{ξ-e,0},则ξ的可信性半方差为:

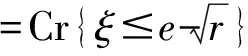
(3)

定理2令ξ和η为期望值有限且相互独立的模糊变量,λ和μ为非负实数,则:

SV(λξ+μη)=λ2SV(ξ)+μ2SV(η)

(4)

定理3设ξ=(a,α,β)是一个三角模糊数。则ξ的可信性期望值和可信性半方差为:

(5)

(6)

2 多阶段投资组合模型

假设证券市场上存在风险资产和无风险资产可供投资。投资者将初始财富W1配置于n+1种资产,并在T期结束时使其财富最大化。假设每个阶段风险资产的收益率为三角模糊变量。符号及说明如表1所示。

表1 符号及说明

2.1 收益、风险和基数约束

假设第t阶段风险资产i的收益率Rit=(ait,αit,βit)是三角模糊变量,采用V型函数来刻画交易成本,xt的净回报率为:

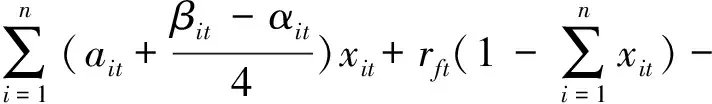
(7)

第t+1期的初始财富为:

(8)

投资组合的可信性半方差可以表示为:

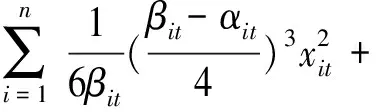
(9)

多阶段投资组合模型的阈值约束可以表示为:lit≤xit≤uit。

θ表示投资者的风险厌恶系数(0≤θ≤1)。θ越大,表示投资者厌恶风险程度越大。假设(1-θ)和θ分别为rNt和SVt(xt)的偏好系数,则投资者效用函数可表示为:

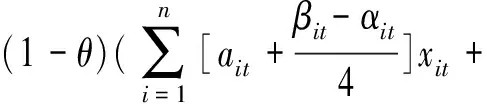
(10)

2.2 多阶段投资组合优化基本模型

投资者希望在整个T期的效用最大化。具有现实约束的多阶段投资组合模型为:

(11)

约束条件(a)是财富动态转移方程;约束条件(b)表示无风险资产的投资比例超过给定下界;约束条件(c)表示xt中非零风险资产的数量不能超过K;约束条件(d)为xit的阈值约束。

3 求解算法

第t阶段的状态变量Wt按由小到大分成4等分,则在每个时期均有5个离散状态变量值。模型(11)可以近似转化为多阶段加权有向图,如图1。有向图的阶段数即投资期数,第t阶段目标函数值和状态变量的离散值分别由多阶段加权有向图第t阶段的权重和点表示。本文运用HEIDERGOTT等[14]的极大代数法求上述多阶段有向赋权图的最长路径。

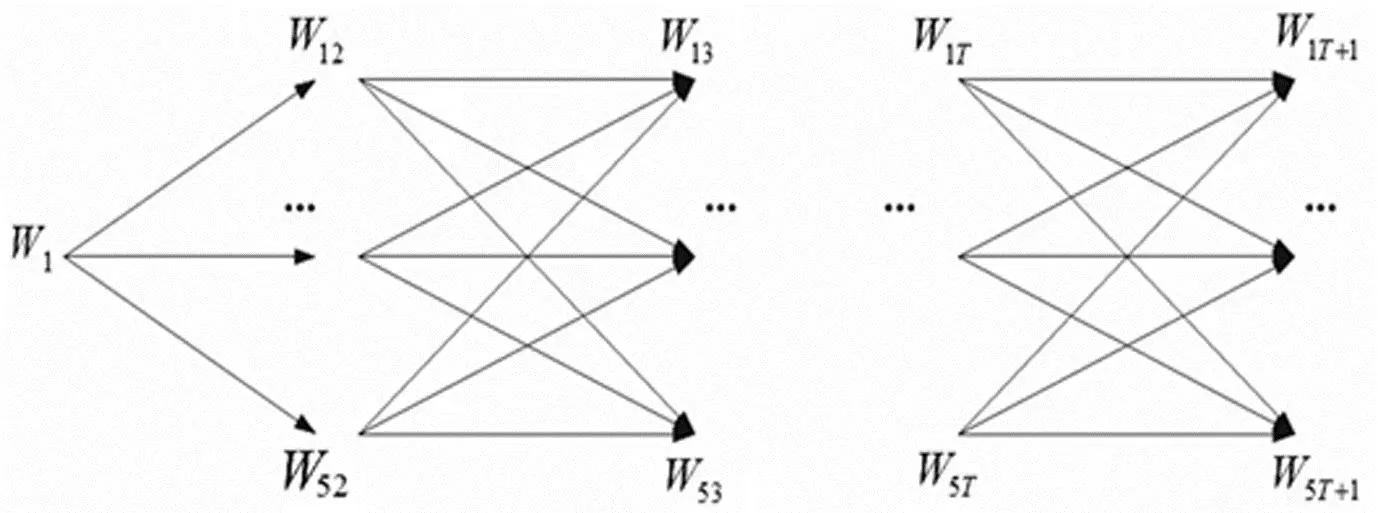
图1 多阶段有向赋权图

3.1 离散近似迭代法

离散近似迭代法的具体步骤:

步骤1确定第t(t=2,…,T+1)阶段的离散状态变量:

假设投资者只考虑在第t阶段使投资组合的半方差最小化:

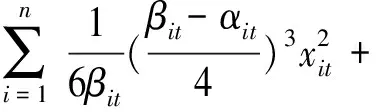
(12)

假设投资者希望第t阶段投资组合期望收益最大化:

(13)

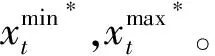
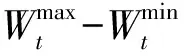
步骤2确定有向赋权图的权重。

步骤3计算多阶段加权有向图的最长路径。

多阶段加权有向图的最长路径F(1)的第一次迭代可以得到如下:

(14)

步骤4离散近似迭代法的第k+1次迭代具体描述如下:

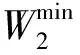
步骤4.3可得第k+1次迭代F(k+1)的最长路径和另一个可行解如下:

(15)

如果|F(k+1)-F(k)|≤10-6,则最长路径F(k+1)的最优解也是模型(11)的近似最优解。否则返回步骤2。

3.2 离散近似迭代法的收敛性

定理4离散近似迭代法是收敛的。

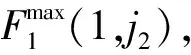
则可得第k次迭代F(k)的多阶段加权有向图的最长路径如下:

(16)

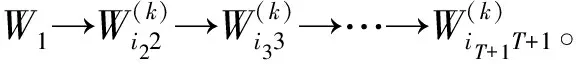
定理证毕。

4 算例

假设投资者从上海证券交易所选择30支股票投资。股票代码分别为S1,…,S30。以W1=1为初期财富进行5期投资,其财富在每个时期的开始可以调整。假定每个时期的收益,风险和30支股票的流动率分别用三角模糊数表示。本文以2006年4月至2015年3月的历史数据为样本,并以每3个月为一个周期进行处理。用VERCHER等[2]计算每个阶段资产收益率的三角可能性分布。

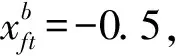
表2 当θ=0.5,K=6时的最优解

表3 当θ=0.5,K=8时的最优解

当θ=0.5,K=6时,第1阶段最优化投资策略投资者分别以20%,20%,20%,20%,20%,20%,-20%,0%的比例分配其初始财富于资产1、资产13、资产17、资产19、资产24 、资产28、无风险资产和30支股票中的其他资产。从表2中也可以得到第2阶段,第3阶段,第4阶段,第5阶段的最优投资策略。最终可用财富为2.0396。当θ=0.5,K=8,最终可用财富为2.2268。从表2和表3可以看出,当K=6和8时,最优解中大部分资产相同。当θ=0.5,K=0,1,…,9时,得到的最终可用财富如表4所示。由表4可知,K=8与K≥9的最优解相同。当K∈[0,8]时,投资组合中非零风险资产数量越多,最终财富越大,它反映了在投资组合优化中所需资产数量的影响。

当K=7,θ=0.1,…,0.9,1时,可得到的最终财富如表5所示。