混合失配模型预测金属/半导体界面热导*

宗志成 潘东楷 邓世琛 万骁 杨哩娜 马登科 杨诺†

1)(华中科技大学能源与动力工程学院,武汉 430074)

2)(北京理工大学宇航学院,北京 100081)

3)(南京师范大学物理科学与技术学院,南京 210000)

声学失配模型和漫散射失配模型被广泛应用于界面热导的计算,两种模型分别建立在极端光滑和粗糙界面的假设基础上.由于实际界面结构与两种假设的区别较大,造成两种模型预测结果与实际界面热导偏差较大.近期提出的混合失配模型考虑了界面结构对声子镜面透射和漫散射透射比例的影响,预测的准确度有所提高.但该模型需要通过分子动力学模拟获取界面声子信息较为复杂.为此,本文通过引入测量的粗糙度数值简化混合失配模型,并增加考虑界面结构对接触面积的影响,实现对界面热导简单快捷、准确地预测.基于该模型,计算预测了金属(铝、铜、金)和半导体(硅、碳化硅、砷化镓、氮化镓)的界面热导.并将铝/硅界面的结果与实验测量结果对比,数据吻合较好.该模型不仅有助于界面导热机理的理解,而且利于与测量结果对比.

1 引言

现代电子器件尺寸的逐渐减小和功率密度的迅速增大,使得散热已成为器件性能和可靠性的最重要挑战之一[1−6].特别是在包含高密度界面结构的纳米器件和结构中,其特征尺寸已缩小到能量载流子平均自由程的量级,原子尺度界面热阻已经无法被忽视[4,7−10],频率更高、密度更大的微电子器件散热问题对增大界面热导的需求更为迫切[11,12].深入理解金属/半导体界面的热输运对于热科学的基础和工程应用,如半导体器件的热管理都是至关重要的.

近年来,界面热输运已经成为学术界和工业界的研究热点[13].Deng等[3]用漫散射失配模型预测了SiC/SiO2和Si/SiO2的界面热导,其预测值与3-omega 实验的测量结果非常吻合.分子动力学(molecular dynamics,MD)被广泛用于界面热输运的模拟,如Yang等[10]模拟了Al/Si 界面的热输运,并发现界面处原子的无序程度是影响界面声子运输的一个重要方面.Peng等[5]研究石墨烯/水界面时发现,引入超晶格结构可以显著增强界面的热输运.Ren等[14]对于石墨烯/六方氮化硼范德瓦耳斯异质结构的研究表明,层间旋转是控制范德瓦耳斯异质结构热输运的一种有效方法.此外,Yang等[8]通过非平衡格林函数(non-equilibrium Green function,NEGF)方法和机器学习算法研究了一维原子链中间层质量分布对界面热导的影响,计算了界面热导极值对应的质量分布.纳米尺度下界面热输运极大依赖于界面结构[13,14],实验发现,界面热阻和以下几种因素有关:粗糙度[15−18]、界面缺陷[17,19,20]和生长方法[21−23]等.

作为经典的界面热输运理论模型,由于其简单易用,声学失配模型(acoustic mismatch model,AMM)和漫散射失配模型(diffuse mismatch model,DMM)被广泛应用于界面热导的预测.然而AMM 和DMM分别建立在极端光滑和粗糙界面的假设基础上,没有考虑具体界面结构,其预测结果与实际界面热导有较大偏差.Zhang等[24]提出了混合失配模型(modified mismatch model,MMM),考虑界面粗糙度及其对声子镜面透射和漫散射透射比例的影响,对界面热导预测更准确,但其需要借助MD 模拟获取界面声子信息,其复杂性限制被更广泛使用.

本文提出利用实验测量得到的粗糙度数值,简化混合失配模型,从而更方便快捷地对界面热导进行预测.首先,根据晶格动力学和第一性原理计算了金属(铝、铜、金)和半导体(硅、碳化硅、砷化镓、氮化镓)的声子热输运参数.随后,基于简化的混合失配模型,计算预测了金属(铝、铜、金)和半导体(硅、碳化硅、砷化镓、氮化镓)的界面声子透射率和界面热导.并将铝/硅界面热导的计算结果与实验测量结果对比,计算准确度得到验证.

2 理论与方法

对于金属/半导体界面,热的载流子包括声子和电子[6].针对电子贡献率的问题,研究人员们开展了诸多工作,如Singh等[25]基于Bloch-Boltzmann-Peierls 公式的研究发现电子-声子耦合对界面热输运的贡献可以忽略;Hamaoui等[26]通过频域光热辐射法研究发现,对于金属/硅界面在高于150 K 时界面热输运主要由声子主导;Giri等[27]则通过时域热反射测量法研究发现,对于金属/半导体界面,只有当电子和声子之间处于高度非平衡的条件下,界面上的电子-声子散射才会对界面热导有贡献.因此,电子-声子耦合对固-固界面热导的重要性仍存在争议[28].当处于平衡条件下时,在金属/非金属界面中电子对界面热导的贡献大多被认为可以忽略[13].因此在本文中仅考虑了声子对界面热导的贡献.

根据Landauer 公式的假设,简化A 和B 是各向同性的德拜固体[29].此时界面热导的理论模型计算结果Gm可以通过(1)式进行预测:

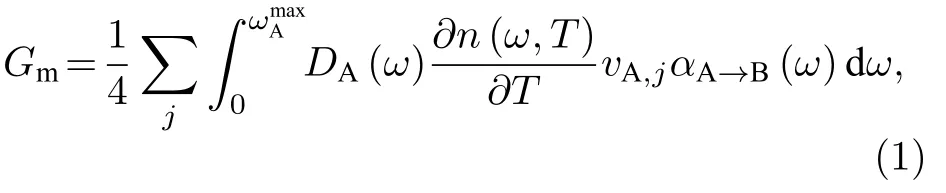
其中ω为频率;为材料A 的声子色散关系截止频率;DA为声子态密度(density of states,DOS);n(ω,T)为玻色-爱因斯坦分布函数;v为声子群速度;αA→B为界面处声子透射系数;下标j表示不同的声子模式.由(1)式可知,只需得到界面两侧材料的声子热输运参数和界面处的声子透射率αA→B,即可得到理论界面热导Gm.在本文中,声子热输运参数主要通过晶格动力学和第一性原理进行计算,而界面处的声子透射率将采用理论模型进行计算.

AMM 和DMM 作为经典的界面声子输运模型,其计算公式为[29]

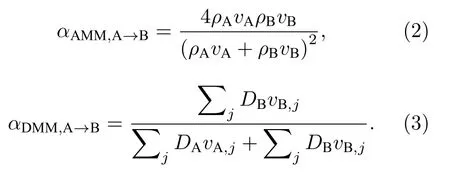
其中ρ为材料的密度.

AMM 假设界面仅发生透射和反射,而DMM假设界面处发生漫散射,但在实际情况中的固-固界面处,声子会同时发生透射、反射和漫散射[30,31].因此,MMM 中用一个假设的镜面参数p来表示声子在界面上的镜面透射比例,则声子漫散射的比例为(1-p),此时的声子透射率通过AMM 和DMM的线性组合来定义[24]:

Ziman等[32]曾指出镜面参数p与均方根粗糙度η和声子波长λ有关,并将这种关系定义为

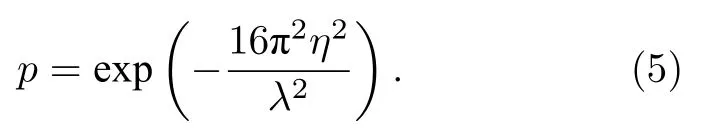
(5)式的关键是界面处的粗糙度η的获得,Zhang等[24]采用MD 模拟了Al/Si 界面,并采用DOS 来表征η的大小,但MD 复杂的建模与模拟时间使得MMM 的使用极为复杂.因此,本文使用先前研究人员测量得到的粗糙度η代入(5)式中得到镜面参数p,进而可以简便使用MMM 模型计算界面热导,并与实验测量的结果进行对比验证.

此外,在实际情况中界面处材料间接触通常存在孔隙、不是理想的完美接触,因此实际接触面积将变小影响导热.为了界面热导预测中增加孔隙对接触面积的影响,本文引入修正接触面积的参数S(界面接触系数).当界面处完美无孔隙时,S=1;对于实际情况,界面处存在孔隙时,S<1.实际情况下的界面热导G可以表示为

其中Gm是理论模型计算得到的界面热导值;S为界面接触系数,当界面处无孔隙时,S=1,当界面处存在孔隙时,S<1.

3 结果和讨论

金属(Al,Cu,Au)和半导体(Si,SiC)的色散关系及DOS 使用晶格动力学软件GULP[33]计算,其中Al 采用Mei-Davenport[34]势函数,Cu 和Au使用EAM[35,36]势函数,Si 使用SW[37]势函数,SiC使用Tersoff[38]势函数.GaAs 和GaN 的色散关系及DOS 使用VASP[39]结合PHONOPY[40]计算.以上3 种金属和4 种半导体材料的声子色散关系及DOS 如图1 和图2 所示.

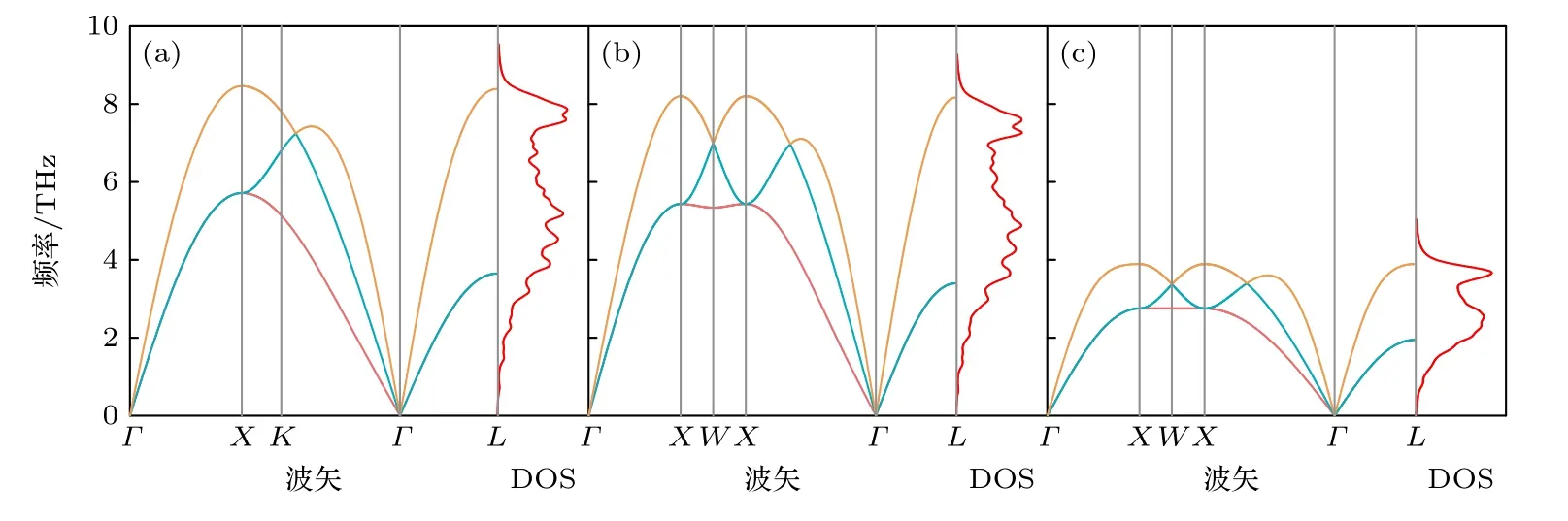
图1 金属的声子色散关系和DOS(a)Al;(b)Cu;(c)AuFig.1.Phonon dispersion relations and DOS of metals:(a)Al;(b)Cu;(c)Au.

图2 半导体的声子色散关系和DOS(a)Si;(b)SiC;(c)GaAs;(d)GaNFig.2.Phonon dispersion relations and DOS of semiconductors:(a)Si;(b)SiC;(c)GaAs;(d)GaN.

图1 和图2 中红色的曲线代表的是DOS,并进行了归一化处理.金属(Al,Cu,Au)均为面心立方结构,原胞中仅有一个原子,因此色散关系曲线中仅有声学支,截止频率由大到小依次为:Al(8.4 THz),Cu(8.1 THz),Au(3.8 THz).对于半导体材料,原胞中不止一个原子,因此色散关系曲线中除了声学支还有光学支的存在.由于在理论模型中,界面仅考虑相同声子模式j间的作用,因此对于半导体材料同样仅考虑声学支对界面热导的贡献,截止频率由大到小依次为:SiC(20 THz),Si(13 THz),GaN(7.1 THz),GaAs(6.2 THz).各模式的声子群速度vj可由声子色散关系曲线得到(声子群速度详见补充材料图S1 和图S2(online)),下面展示金属Al 和半导体(Si,SiC,GaAs,GaN)界面热导的计算过程.

在计算界面声子透射率频谱之前,首先需要确定声子传输的方向.在理论模型计算界面热导(G)时DMM 不存在方向性的问题,即GDMM,A→B=GDMM,B→A.但AMM 存在方向性的问题.AMM中声子入射角和透射角服从Snell 定律,当材料A的声子群速度大于材料B 的声子群速度时,来自材料A 的声子能以任意入射角通过界面传输.而在反方向,材料B 的入射角不能超过临界角,以避免全反射[28,29].因此在本文DMM 和MMM 的计算中均选择声子群速度较大一侧向群速度较小一侧传输.

对于Al 和半导体(Si,SiC,GaAs,GaN)可根据(2)—(5)式,分别计算AMM,DMM 和MMM(粗糙度:0.28 nm,1.38 nm,2.16 nm)三种模型下的界面声子透射率频谱如图3 所示,同样可以计算金属(Cu,Au)和半导体(Si,SiC,GaAs,GaN)界面的声子透射率频谱(详见补充材料图S3 和图S4(online)).对于Al/Si,Al/GaAs 和Al/GaN 界面,在大多数频率下AMM 计算所得的界面声子透射率要高于DMM 的计算结果.这是因为AMM 假设入射界面处的声子通过镜面透射,不发生散射,因此透射概率由声学阻抗失配决定.相反,DMM假设界面是完全无序的,所有声子都是扩散散射的.而对于Al/SiC 界面,则是DMM 计算结果更高,而对于Al/SiC 界面两侧材料阻抗失配较大,此时DMM 预测的结果大于AMM 的结果[29].

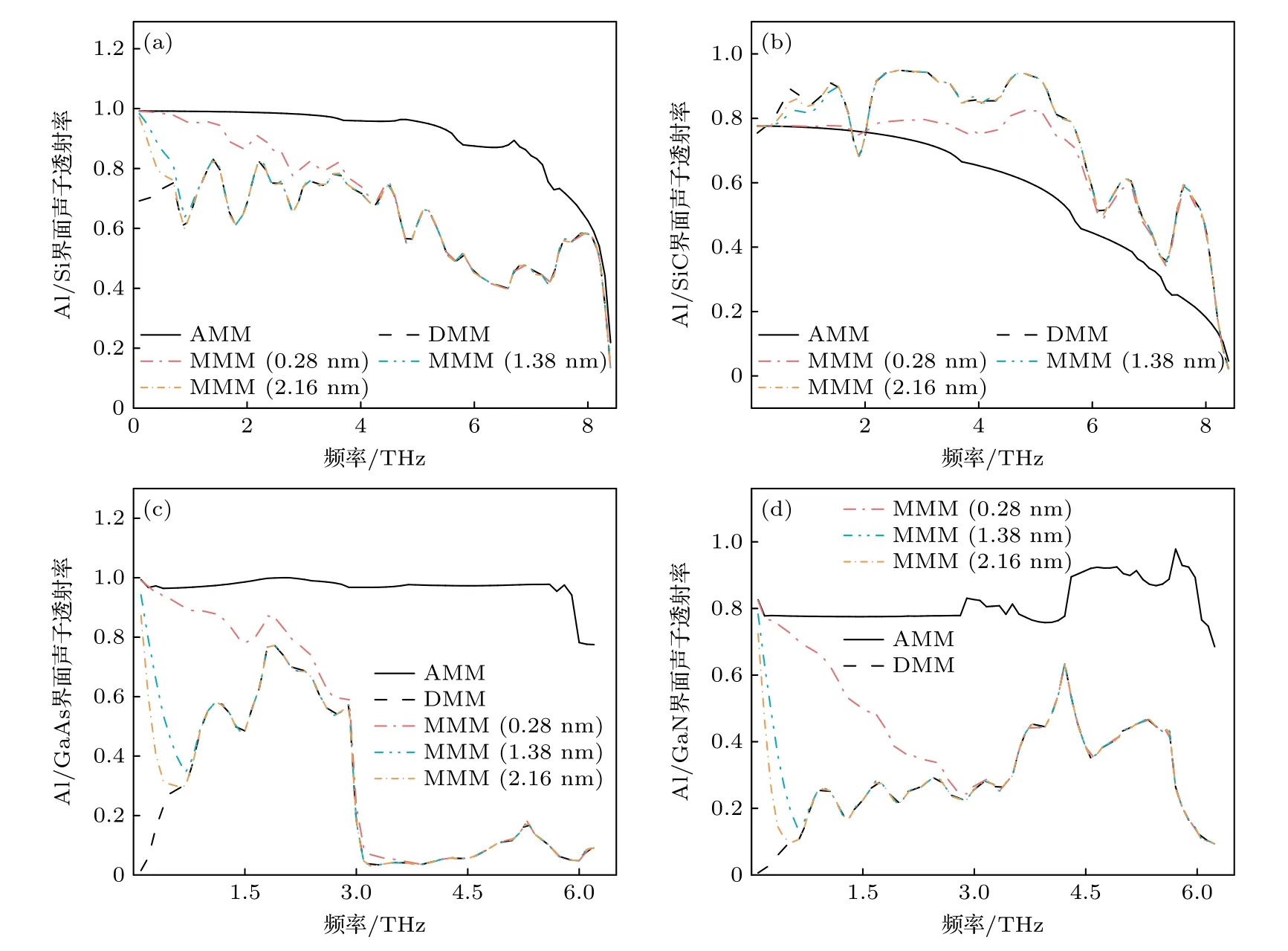
图3 AMM,DMM 和MMM(粗糙度:0.28,1.38,2.16 nm)三种模型计算界面声子透射率频谱对比(a)Al/Si 界面;(b)Al/SiC界面;(c)Al/GaAs 界面;(d)Al/GaN 界面Fig.3.Comparison of phonon transmittance spectra calculated by AMM,DMM and MMM(roughness:0.28,1.38,2.16 nm):(a)Al/Si interface;(b)Al/SiC interface;(c)Al/GaAs interface;(d)Al/GaN interface.

将声子输运参数和声子透射率代入(1)式中即可得到界面热导随温度变化的曲线.此外,在理论模型计算前,参考界面接触力学理论[41],得到界面接触系数S与界面粗糙度的关系,如图4 所示.其中,ηmax为界面两侧材料的原子间经验势函数截止半径,当界面粗糙度大于这个值时,认为界面接触系数趋近于0,对于Al/Si 界面,该值为4.7 nm(其他界面的ηmax详见补充材料表S1(online)),其他金属/半导体界面同样可采用上述方法得到界面接触系数S与界面粗糙度的关系.

图4 界面接触系数S 和粗糙度之间的关系,其中ηmax 为界面两侧材料的原子间经验势函数截止半径,当界面粗糙度大于这个值时,认为界面接触系数趋近于0,对于Al/Si界面,该值为4.7 nmFig.4.Relationship between interface contact coefficientS and roughness,whereηmax is the cutoff radius of the interatomic empirical potential function of the materials on both sides of the interface.When the roughness of the interface is greater than this value,the interface contact coefficient is considered to approach 0,which is 4.7 nm for Al/Si interface.

将系数S代入(6)式中即可计算不同温度、不同粗糙度下的理论模型结果,如图5 所示.并与Al/Si 界面实验测量值进行对比,得出结论:MMM计算的界面热导值与实验测量值吻合度较高.

从图5 可以看出,界面热导的大小随着温度升高逐渐趋于饱和.在此过程中,声子群速度、DOS和界面透射率均保持不变.界面热导的变化的原因是玻色-爱因斯坦分布,在低温条件下,只有低频声子对界面热导有贡献.因此,当温度升高时,更多频率较高的声子被激发参与界面热输运,从而增加了界面热导.当温度足够大时,激发的声子数饱和,温度的升高将不会再使更多的声子参与界面热输运.因此,界面热导会处于饱和状态.

图5 AMM,DMM 和MMM(粗糙度:0.28,1.38,2.16 nm)预测界面热导随温度的变化(a)Al/Si 界面;(b)Al/SiC 界面;(c)Al/GaAs界面;(d)Al/GaN 界面;实验值来源于Hopkins等[16]的测量Fig.5.Curves of interfacial thermal conductance predicted by AMM,DMM and MMM(roughness:0.28,0.53,1.38 nm)models as a function of temperature:(a)Al/Si interface;(b)Al/SiC interface;(c)Al/GaAs interface;(d)Al/GaN interface.The experimental values were obtained from measurements made by Hopkins et al.[16].

对于其他金属(Cu,Au)和半导体(Si,SiC,GaAs,GaN)界面同样可根据上述流程计算界面热导随温度变化曲线(详见补充材料图S5 和图S6(online)),同时在理论模型计算时,采用了图4 中同样方法得到不同界面的接触系数S,以上界面热导在不同粗糙度下的计算结果如图6 所示,可以发现,对于金属/半导体界面,当粗糙度增大时,界面热导普遍会减小,这与前人的研究结论一致[15,16,18,28].

图6 MMM 模型预测300 K 时的金属(Al,Cu,Au)和半导体(Si,SiC,GaAs,GaN)界面热导,其中粗糙度取值为0.28,1.38,2.16 nmFig.6.Interfacial thermal conductance of metal(Al,Cu,Au)and semiconductor(Si,SiC,GaAs,GaN)interfaces predicted by MMM model at 300 K,roughness values:0.28 nm,1.38 nm,2.16 nm.

从图6 可以发现,Al/半导体界面和Cu/半导体界面热导的预测结果十分相似,但与Au/半导体界面相差较大.Al 和Cu 声子色散关系和DOS 极其相似,参与到界面热输运的声子频率近似,但金的声子色散关系截止频率低,使得只有较少的低频声子参与到界面热输运中.同时可以看出在金属/半导体界面中,Al,Cu 组成的金属/半导体界面热导要普遍更高,主要原因是相比Au,金属(Al,Cu)声子色散关系截止频率较高,与半导体材料的DOS重合度高,同时对于声子色散关系截止频率较高的金属,如钼(Mo)[42]、铬(Cr)[43]、镍(Ni)[44]也可得到较高的界面热导;而其他声子色散关系截止频率较低的金属,如铂(Pt)[44]、钌(Ru)[45]、钨(W)[46]只能得到相对较低的界面热导.

而从半导体的角度对比发现,在金属(Al,Cu)/半导体界面中,Si 和GaN 组成的界面热导更高,而热导率较高的SiC 在金属/半导体界面中界面热导偏低,主要是因为SiC 的声学支截止频率远高于Al 和Cu,而Si 和GaN 的声学支截止频率与Al 和Cu 相对接近,DOS 重合度更大,界面热输运中有更多声子参与.声学支截止频率较低的半导体如氧化锌(ZnO)[47]、氧化镓(Ga2O3)[48]、磷化铟(InP)[49]则只能得到较低的界面热导.而对于GaAs 而言,Au 的色散关系截止频率更加近似,DOS 重合度更高,因此Au/GaAS 界面热导要大于Au/半导体(Si,SiC,GaN)界面.

4 总结和展望

综上,本文通过考虑界面粗糙度和界面结构对金属/半导体界面热导的影响,提出预测界面热导的简化混合失配模型.通过将铝/硅界面的预测结果与实验测量结果进行比较,验证了简化混合失配模型的正确性.基于该模型,本文计算预测了金属(铝、铜、金)和半导体(硅、碳化硅、砷化镓、氮化镓)的界面热导,计算结果表明金属/半导体界面热导会随温度的升高而增大,但当温度较高时,界面热导增幅减缓.此外,充分考虑界面结构的计算结果表明界面热导会随粗糙度的增大而降低.简化混合失配模型具有使用简单、预测结果准确的特点,有利于对界面热导预测以及与实验测量结果进行对比和分析.

混合失配模型考虑了界面粗糙度的影响,以实现较为精确的预测.因其基于传统的声学失配模型和漫散射失配模型,所以无法考虑高温时多声子散射过程对界面热阻的影响.此外,界面处的结构形变会导致出现新的界面声子模式[10,50,51],进而影响界面热阻.借助分子动力学,混合失配模型可以考虑界面声子模式的影响[24].本文在简化模型的同时,无法考虑界面声子模式的影响.