新型压缩感知计算模型分析三维电大目标电磁散射特性*

王攀 王仲根† 孙玉发 聂文艳

1)(安徽理工大学电气与信息工程学院,淮南 232001)

2)(安徽大学电子信息工程学院,合肥 230601)

3)(淮南师范学院机械与电气工程学院,淮南 232001)

为提高基于压缩感知技术的矩量法在三维电大目标双站电磁散射问题中的计算效率和稳定性,提出新的稀疏、测量和重构方法,构建一种新型压缩感知计算模型.不同于基于欠定方程的传统的压缩感知计算模型,新型计算模型首先采用按行均匀抽取阻抗矩阵的方法构造测量矩阵以获得稳定的计算结果;然后,基于Foldy-Lax 方程生成多阶特征基函数并作为稀疏基对感应电流进行稀疏转换;再依据少数低阶特征基函数足以近似表征感应电流的先验条件,将恢复算法简化为最小二乘法;最后,将矩阵方程转换为一个超定系统并采用最小二乘法解出电流系数.与传统的计算模型相比,新型计算模型不仅可以获得更加稳定的精确解,还可以显著提高电大目标双站散射问题的求解效率和计算精度.数值仿真结果证明了新方法的可行性和高效性.

1 引言

作为求解电磁散射问题的有效数值方法之一,矩量法[1](method of moments,MoM)可以将电磁场积分方程离散为一个线性矩阵方程.由于其生成的阻抗矩阵为稠密矩阵,对于电大尺寸问题,求解该矩阵方程将消耗大量的时间和内存.为提高计算效率,提出了一些有效的快速算法,如多层快速多极子法[2]、复合基函数法[3]、高阶MoM[4]和特征基函数(characteristic basis function,CBF)法[5,6]等.近年来,压缩感知(compressive sensing,CS)[7]技术被成功引入到MoM 中,为上述问题提供了新的解决方案,并形成了两种主要的计算模型:分别是基于新型激励源的计算模型和基于欠定方程的计算模型.

基于新型激励源的计算模型由陈明生等[8]于2011 年提出,该技术的基本原理是通过压缩入射激励以减少矩阵方程的求解次数,从而提高多激励散射问题的求解效率.在此模型基础上,相关学者对模型框架内中的稀疏、测量以及重构等关键技术进行了深入研究[9−11],并将该方法的应用扩展至复杂结构目标的散射问题[12,13].然而,该技术仍然采用传统方法求解MoM 中的矩阵方程,无法用于双站散射问题分析.与第一种模型不同,王哲等[14]于2014 年提出的基于欠定方程的计算模型直接改变MoM 的算法结构,使其满足CS 框架,继而引入CS 技术快速重构待求电流.该方法将矩阵方程缩减为一个欠定系统,显著减少了矩阵方程的求解时间.然而,该计算模型中的一些关键技术仍需要进一步改进.首先,在测量矩阵的构造中,随机抽取阻抗矩阵[14,15]或左乘随机高斯矩阵[16,17]的方法造成了计算结果的不确定性;其次,在使用Rao-Wilton-Glisson(RWG)基函数的三维问题中很难构造合适的稀疏基.Cao等[18]采用Krylov 子空间构造稀疏基的方法实现了对三维目标感应电流的稀疏转换,但是稀疏基的构造需要大量的矩阵乘积运算,并不适用于电大尺寸问题.Ding等[19]利用具有特征基函数的基于CS 技术的MoM 方法(CSCBFs)同样实现了对三维目标感应电流的稀疏转换,并且采用区域分解策略使其更适用于电大尺寸问题,然而对于复杂目标,该方法的计算精度有待提高.Wang等[20]采用基于区域分解的特征模构造稀疏基,避免了阻抗矩阵的完全填充以提高计算效率,然而该方法中基函数数量以及测量矩阵的维数显著较大.最后,由于缺乏先验知识,基于欠定方程的计算模型在具体问题中很难设定合适的稀疏度和观测次数等关键参数.

本文提出一种新型CS 计算模型(NCS-CBFs)用于求解三维电大目标双站电磁散射问题.首先,采用按行均匀抽取阻抗矩阵的方法构造测量矩阵以获得稳定的计算结果;然后,基于Foldy-Lax 方程生成多阶CBFs 用于构造稀疏转换矩阵,以降低基函数的个数和构造时间;再依据低阶CBFs 的特性获取先验条件,将恢复算法简化为最小二乘法;最后构造一个超定方程,并采用最小二乘法解出电流系数.NCS-CBFs 与CS-CBFs 相比,显著降低了计算时间,提高了计算精度.最后结合具体算例,给出了与CS-CBFs 的比较结果,证明了NCS-CBFs的有效性.

2 基本原理

2.1 基于欠定方程的CS 计算模型

结合CS 技术的MoM 的基本思想是将感应电流作为待重构信号,压缩的阻抗矩阵和激励分别作为测量矩阵和测量值,从而将矩阵方程转变为一个欠定系统.在MoM 中,以RWG 函数作为基函数和权函数,将积分方程离散成如下矩阵方程:

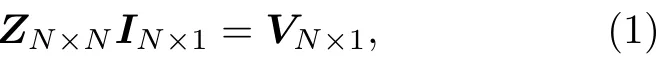
式中,Z表示满秩的阻抗矩阵;I表示RWG 基函数的权重系数向量,又称为感应电流;V为激励向量;N为RWG 基函数的数量,即未知数的数量.随机抽取Z和V中的M行分别构造测量矩阵和测 量值,则将(1)式转变为如下欠定方程:

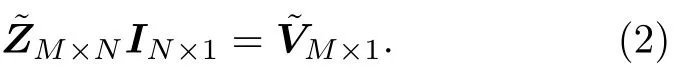
由于I本身不稀疏,为满足CS 框架,需对I进行稀疏 转换:

式中,Ψ为稀疏转换矩阵,a为稀疏基的权重系数向 量.将(3)式代入到(2)式,可得

式中,Θ为传感矩阵.根据CS 理论,当Θ满足限制等距性质[21],则可采用恢复算法得到精确解.通常恢复算法选择计算复杂度较小的贪婪算法,例如广义正交匹配追踪算法(generalized orthogonal matching pursuit,GOMP)[22].

在上述基于欠定方程的CS 计算模型中,随机构造的测量矩阵不可避免地导致结果存在不确定性.此外,对于电大尺寸问题,由于未知数N较大,构造N×N维的稀疏转换矩阵比较困难.对于三维问题,文献[20]采用CBFs 构造Ψ.首先将目标划分为m块较小的子域,并对每块子域进行扩展以保障电流在边界处的连续性.然后,分别计算每块子域的主要特征基函数(PCBFs)与次要特征基 函数(SCBFs):

显然,该方法对I稀疏转换的同时进行了降维,此时Ψ的维数为m2×m2.由于CS-CBFs 只采用一阶SCBFs,包含的子域间的互偶信息较少,在计算复杂目标时精度不高.

2.2 新型CS 计算模型

为提高基于CS 的MoM 的计算效率和结果的稳定性,本文提出新的稀疏、测量和重构方法,构造一种新型CS 计算模型(NCS-CBFs).首先采用基于Foldy-Lax 方程的多阶CBFs[6]构造稀疏转换矩阵.其中PCBFs 的构造方法与CS-CBFs 方法相同,根据(5)式得到出全部子域的PCBFs.然后,对于每块子域,将其他子域的PCBFs 所产生的散射场的叠加作为入射场用于构造一阶SCBFs:

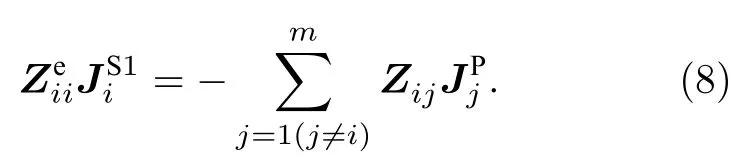
类似地,二阶及以上的高阶SCBFs 由上一阶的SCBFs 构造:

显然,构造一个N×N维的JC是非常耗时的.考虑到SCBFs 在物理意义上表现为子域间的互偶效应,越高阶的互偶效果越微弱,也就是高阶的SCBFs 对感应电流的贡献更小,可由此作为先验条件对恢复算法GOMP 进行简化.在GOMP 中,每次迭代的第一步为“识别”传感矩阵Θ中与残差最相关的列,然后采用最小二乘法解出电流系数a.由于最相关的列对应的基函数对电流的贡献最大,再结合上述先验条件可知,PCBFs 和一些低阶的SCBFs 对应的Θ中的列就是所要“识别”的列,这些CBFs 的个数便是I在JC上的稀疏度.因此,在确定少数低阶CBFs 后,可以省去GOMP 中的“识别”步骤,直接采用最小二乘法解出a.根据以上分析可知,仅需计算少数低阶的CBFs.

假设计算至K阶(含PCBFs),共获得LmK个CBFs,L为基函数数量,则(10)式中的为

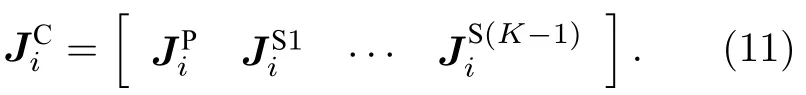
将(10)式代入到(2)式可得

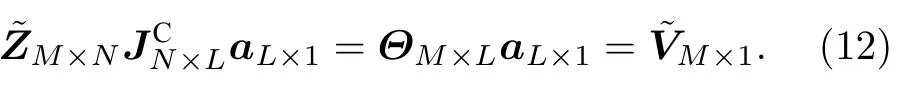
NCS-CBFs中M取L的3—5 倍,此时(12)式为一个 超定方程.然后采用最小二乘法求解a:

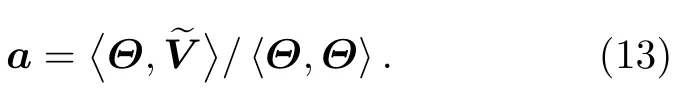
最后,将a代入到(10)式得到感应电流I.

对于测量矩阵的构造,采用按行均匀抽取阻抗矩阵的方式,即按固定行距间隔进行抽取,行距间隔约为N/M.首先,由于阻抗矩阵在形式上为RWG函数离散的满秩矩阵,与作为宏域基函数的CBF具有不相关性,由此构造的传感矩阵各列之间不相关.其次,王哲等[14]证明了对应阻抗矩阵行向量的权函数具有冗余性,然而由于目标表面电流分布情况未知,即以RWG 函数作为权函数的冗余情况未知,因此在缺少先验知识的情况下,可以认为阻抗矩阵的每一行作为一次对电流系数的观测具有相同的意义.故均匀抽取和随机抽取所获得的测量矩阵具有相似的随机特性和等价的形式意义.王哲等[14]同时指出测量矩阵的规模是决定获得高精度解的主要因素.由以上分析可知,均匀抽取阻抗矩阵所构造的测量矩阵与随机抽取相同,可以保障电流系数被精确重构.一旦确定M的值,即可构造一个确定性的测量矩阵,从而获得稳定的计算结果.

与文献[19]相比,NCS-CBFs 不仅实现了对三维目标感应电流的稀疏和降维,而且改进了稀疏转换矩和测量矩阵的构造方式,并简化了恢复算法.此外,NCS-CBFs 的算法结构与基于欠定方程的计算模型不同,最终生成的求解模型为一个超定系统.由于NCS-CBFs 生成的基函数更少(K＜m),传感矩阵维数更低,且简化了恢复算法,可以显著降低构造基函数和重构电流系数的时间.

3 计算复杂度分析

NCS-CBFs 和CS-CBFs 的计算过程主要分为三个部分:填充阻抗矩阵、构造基函数以及重构电流系数.为便于分析,假设目标被划分为m个同等大小的子域,每个子域内的未知数均为Ni,并忽略子域扩展部分对计算的影响.

填充阻抗矩阵:对于填充阻抗矩阵部分,两种方法均需填充矩阵的全部元素,其计算复杂度均为O(N2).

重构电流系数:在CS-CBFs 中生成的基函数的数量为m2,重构电流时采用GOMP 迭代求解.该方法中构造传感矩阵的计算复杂度为O(MNm2),迭代求解复杂度为O(sMm2),其中S为迭代次数.在NCS-CBFs 中,生成的基函数数量为L=mK,其构造传感矩阵的计算复杂度为O(MNL).重构电流采用了简化的GOMP 方法避免了迭代求解,其计算复杂度为O(ML).由于L≪m2,且抽取的行数M为基函数的固定倍数,NCS-CBFs 构造的测量矩阵及传感矩阵的维数更低.因此NCS-CBFs比CS-CBFs 在重构电流系数中具有更低的计算复杂度.

综述所述,NCS-CBFs 在构造基函数以及重构电流系数部分计算复杂度比CS-CBFs 更低,可以有效减少计算时间.

4 数值算例

为了证明NCS-CBFs 的有效性,分别采用NCSCBFs 和CS-CBFs 对不同三维导体模型进行数值仿真,其中CS-CBFs 采用GOMP 算法.所有算例均在Intel(R)Core(TM)i7-10750H 2.60 GHz,64 GB RAM 的PC 机上完成.为了分析计算精度,定义目标双站雷达散射截面(radar cross section,RCS)的均方根误差为

式中,σcal,i为所用方法的计算结果,σref,i为传统MoM 的计算结果,Na为采样点个数.

算例1计算了一个边长为1 m 的导体立方体模型的双站RCS.入射平面波kinc的频率为800 MHz,入射角度为θ=0°,φ=0°,其中θ和φ分别代表球坐标系中的天顶角和方位角.采用RWG 基函数离散目标表面为16206 个三角形面元,产生24309 个未知数.将目标划分为26 块子域,每块子域扩展0.15 倍波长,扩展后的未知数个数为33772.

首先,分别计算CS-CBFs 和NCS-CBFs 在不同抽取方式下构造的测量矩阵与稀疏基之间的相关系数[15],如表1 所列.其中,被抽取的行数约为所生成的基函数数目的4 倍,NCS-CBFs 计算至13 阶CBFs.由表1 可知,在四种方法中构造的测量矩阵与稀疏基之间均为不相关或弱相关.由此可知,测量矩阵的行与稀疏基的列不能相互稀疏表示,测量矩阵可以保障电流系数被精确重构.为进一步验证NCS-CBFs 计算结果的稳定性和精确性,采用CS-CBFs 和NCS-CBFs 在不同抽取方式下分别进行5000 次仿真实验.所得到的RCS 误差按升序排列,如图1 所示.从图1 可以看出,采用随机抽取方法时,每次计算结果不相同,其RCS 误差在一定范围内浮动.而采用均匀抽取方法时,两种算法均可获得固定的计算结果,其RCS 误差约为随机抽取时多次计算的平均值.图2 给出了采用随机抽取方法的CS-CBFs 在5000 次实验中取得最大误差和最小误差时的双站RCS.由图2 可知,在取得最大误差时其计算结果出现明显偏差,因此采用均匀抽取方法获得稳定的计算结果更为可靠.为准确对比两种方法的精度情况,之后的算例中两种算法均采用了均匀抽取方式.

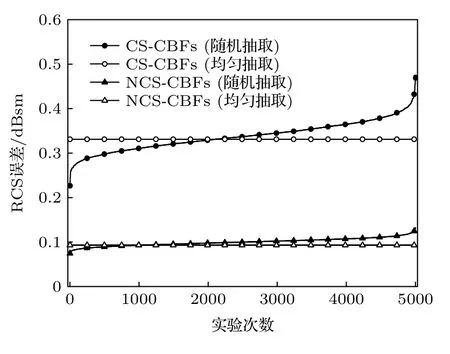
图1 5000次实验的RCS 误差分布Fig.1.RCS error distribution of 5000 experiments.

图2 随机抽取方法下CS-CBFs的不同计算结果对比(φ=0°)Fig.2.Comparison of different calculation results of CSCBFs with randomly extracting(φ=0°).

表1 测量矩阵与稀疏基之间的相关系数Table 1.Correlation coefficient of the measurement matrix and sparse basis.

图3 给出了两种方法中抽取行数M与RCS误差、求解时间的关系,其中求解时间包括生成基函数时间、构造和求解超定方程时间.在NCSCBFs 中,计算至13 阶CBFs.从图3 可以看出,RCS误差随着M的增加而减小,在M为基函数数量的3 倍以上时,计算精度趋于稳定.此外,M的增加会造成传感矩阵Θ的维数增大,求解时间也相应增加.因此,NCS-CBFs中M设为基函数数量的3—5 倍即可获得较高的效率和精度.

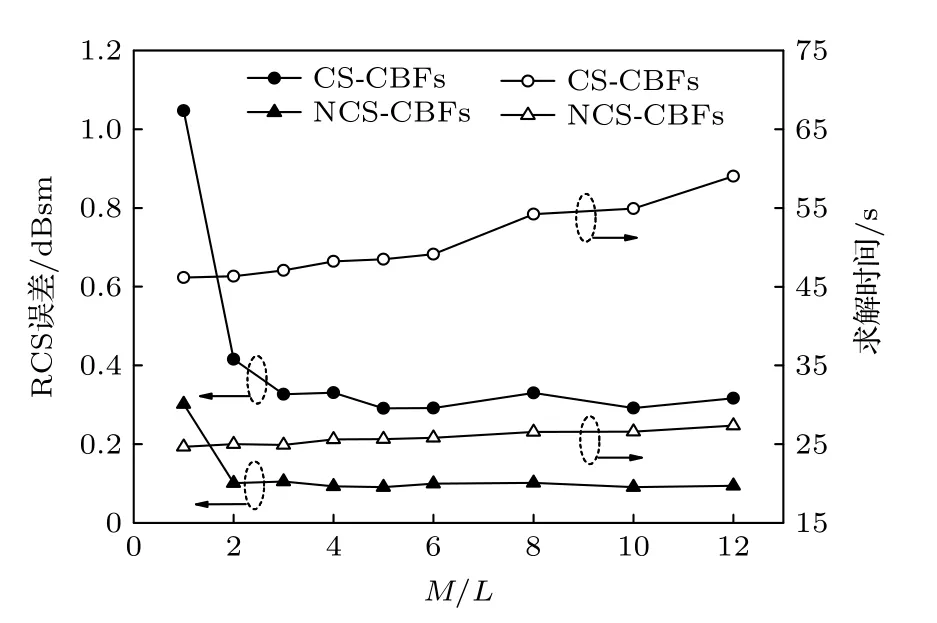
图3 不同抽取行数下两种方法的RCS 误差和求解时间Fig.3.RCS error and solution time of two methods with different number of extracted rows.

在NCS-CBFs 中,由于感应电流在CBFs 稀疏基上不是严格稀疏,少数低阶的CBFs 只能近似地表述感应电流,因此参与计算的CBFs 阶数越多计算结果越准确.图4 给出了RCS 误差和求解时间与参与计算的CBFs 阶数的关系,其中M取基函数数目的4 倍.从图4 可以看出,较高的CBFs阶数可以获得更精确的结果,但是同时带来求解时间的快速增加.为平衡效率和精度,本文中计算的阶数取在m/2左右.采用CS-CBFs 和NCS-CBFs分别计算了立方体的双站RCS,计算结果见图5,其中抽取行数均为基函数的4 倍.CS-CBFs 方法生成676 个CBFs,其传感矩阵的维数为3039 ×676.NCS-CBFs 方法计算至13 阶生成338 个CBFs,其传感矩阵的维数1430×338.从图5 可以看出NCS-CBFs 与MoM,CS-CBFs 的计算结果吻合较好,计算精度较高.

图4 不同基函数阶数下本文方法的RCS 误差和求解时间Fig.4.RCS error and solution time of the proposed method for different orders of basis functions.

图5 立方体水平极化双站RCS(φ=0°)Fig.5.Bistatic RCS of cube in horizontal polarization(φ=0°).

算例2计算了一个导体圆柱体模型的双站RCS,其底面半径为0.2 m,高为1 m,入射频率为2 GHz.采用RWG 基函数离散目标表面为27174 个三角形面元,产生40761 个未知数,目标被划为40 块子域,每块子域扩展0.15 倍波长,扩展后未知数的个数为58126.两种方法均采用均匀抽取方式,抽取行数为基函数数量的4 倍.CS-CBFs 中生成1600 个CBFs,传感矩阵维数为6794×1600.NCS-CBFs 中计算至18 阶生成720 个CBFs,传感矩阵维数为2912×720.两种方法计算的结果如图6 所示,可见,NCS-CBFs 的计算结果与MoM,CS-CBFs 吻合较好,具有较高的计算精度.

图6 圆柱体垂直极化双站RCS(φ=0°)Fig.6.Bistatic RCS of cylinder in vertical polarization(φ=0°).

算例3计算了一个导弹模型的双站RCS,其长为1 m,宽为0.64 m,入射频率为2 GHz.剖分目标表面为14132 个三角面元,产生21198 个未知数,目标被划为24 块子域,每块子域扩展0.15 倍波长,扩展后未知数的个数为33159.两种方法均采用均匀抽取方式,抽取行数为基函数数目的4 倍.CS-CBFs 得到576 个CBFs,传感矩阵的维数为2304×576.NCS-CBFs 计算至12 阶得到288个CBFs,传感矩阵的维数为1152×288.两种方法的计算结果如图7 所示,NCS-CBFs 在较复杂目标问题中可以获得比CS-CBFs 更高的精度.

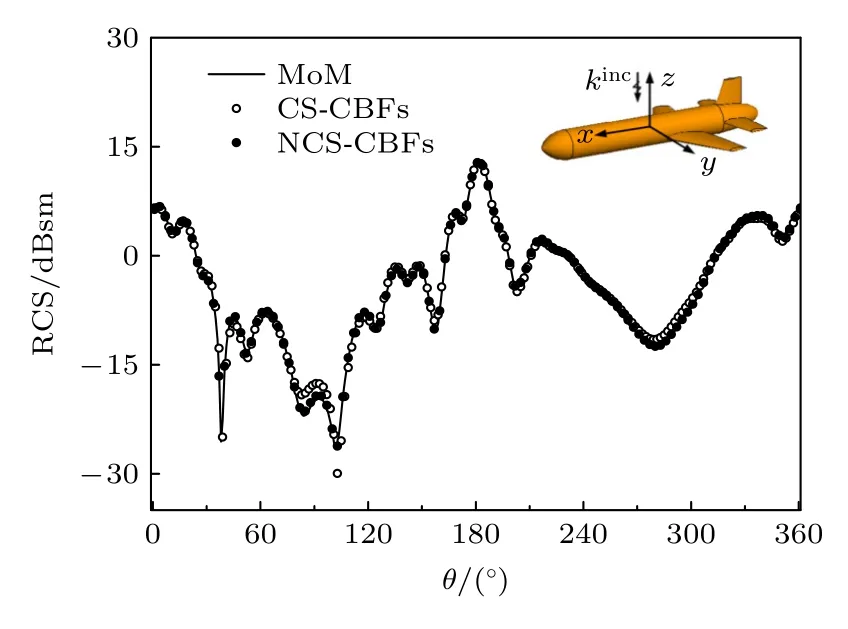
图7 导弹水平极化双站RCS(φ=0°)Fig.7.Bistatic RCS of missile in horizontal polarization(φ=0°).

表2 列出了对应于图5—7 的仿真时间和RCS误差.从表2 可以看出,与CS-CBFs 相比,NCSCBFs 显著降低了构造基函数以及重构电流系数的时间.三个仿真实验的总求解时间分别减少了47%,40%和68%,求解效率得到大幅度提升.此外,NCS-CBFs 得到的RCS 误差均低于CS-CBFs,新方法具有更高的计算精度.

表2 计算时间和RCS 误差比较Table 2.Comparison of computation time and RCS error.

5 结论

针对基于CS 的MoM 关键技术,本文提出了新的稀疏、测量和重构方法,构建了一种新型CS计算模型——NCS-CBFs.相比传统的CS-CBFs,NCS-CBFs 不仅可以获得稳定的计算结果,还提高了计算效率和精度,仿真结果证明了NCS-CBFs的有效性.与基于欠定方程的计算模型相比,NCSCBFs 将矩阵方程压缩为尺寸更小的超定方程进行求解,更适用于电大尺寸问题,并可与快速偶极子法、自适应交叉近似算法等加速算法相结合进一步提高计算效率.