基于GARCH-JSU分布模型对风险价值评估的实证研究
2023-02-19陈媛媛李翠霞
陈媛媛 李翠霞
(1.福州工商学院文法学院 福建福州 350715;2.徐州工程学院数学与统计学院 江苏徐州 221018)
风险价值(VaR)是在选定的一段时间内,某一置信水平上以货币单位或占投资组合价值百分比的最大损失。1993年,G30集团在研究金融衍生品类别的基础上,提出了度量市场风险的VaR方法。1994年,摩根大通推导出了用于计算VaR的风险控制模型(RiskMetrics),提高了该公司的知名度。随后,巴塞尔银行监管委员会提出,可以使用内部VaR模型确定银行进行的交易活动必须满足的资本要求。在此领域出版了多部著作,如Jorion(1996)[1]和Dowd(1998)[2]等解释了VaR背后的统计基础;Jorion(2000)[3],Mittnik和Rachev(2000)[4],Duffie和Pan(1997)[5]给出了VaR的一般解释。市场上大部分投资者对VaR的衡量主要通过在预定的置信水平上由于市场下行影响而造成在接下来的一段时间内可能产生的最大损失,计算结果主要依赖选取的条件分布的尾部状态,随着GARCH模型成功地应用于对波动率进行建模,GARCH模型对VaR的研究成为一个重要的研究领域。Francq (2015)[6]认为,对参数形式εt=σt(θ0)ηt的这种GARCH模型来说,VaR值的计算结果主要依赖对tη所设定的分布形式,而不依赖波动率参数 0θ。本文在Francq思路的基础上,使用了一种新的条件分布形式——JSU(Johnson SU)型分布,为上证综合指数建立了条件方差模型,并与之前提出的传统分布形式,即正态分布、学生t分布、广义误差分布(GED)进行比较。
1 模型基本原理
1.1 风险价值(VaR)
VaR(Value at Risk) 是指在确定的一段时间内,投资组合在某一置信水平上产生的最大损失,即
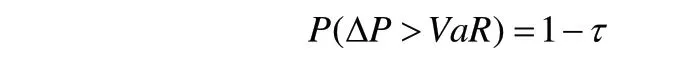
其中,P表示概率度量;ΔP=P(t+Δt)-P(t)表示投资组合在持有期Δt内产生的损失;P(t)表示投资组合当下t时刻的实际价值(通常看作收益率);τ为置信水平,VaR值代表在置信水平τ上可能产生的最大损失值。通过上述表达式可以看出,VaR是关于Δt(持有期)和τ(置信水平)的函数,并且其计算结果随着Δt和τ的增加而增加。因此,排除其他外在因素的影响,VaR值由持有期和置信度两个参数决定。本文均采用一天的持有期进行计算。
1.2 Johnson SU型分布
Johnson分布体系是由Johnson(1949)对服从标准正态分布的随机变量进行不同变换得到的,其中主要包括三种类型:对数正态系统(SL)、有界系统(SB)、无界系统(SU)。表1给出了Johnson分布体系及其与各种变换形式之间的对应关系。由于随机变量取值范围的限制,SL型和SB型均不适用于对金融时间序列的分布进行拟合,因而SU型分布受到金融计量建模者的广泛关注[7]。

表1 Johnson分布体系及变换

在JSU分布中,当偏度参数γ>0(γ< 0)时,分布呈现右(左)偏;当γ=0时,分布呈现对称。此外,当峰度参数δ取值越大时,分布的峰值越高。由于JSU分布与Norm分布存在变换关系,因此这类分布的分位数、密度函数、分布函数均可由标准正态分布的对应参数经变换得到。不同于其他(如学生t、非对称或有偏的学生t等)分布,Choi等[8]推导出JSU分布的前四阶中心矩,由此说明JSU分布的所有高阶矩均有限,使其更易于描述金融资产的非对称性和厚尾特征。
1.3 模型表示
GARCH(1,1)-JSU模型表示如下:
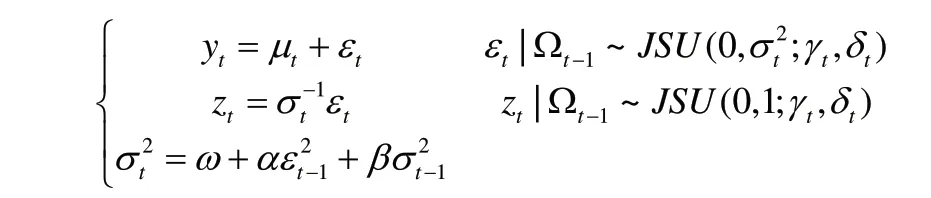
其中,μt=Et-1(yt)为条件均值;Ωt-1为t-1时刻前的信息集;εt为残差项,zt是εt标准化后的误差项;γt为时变的偏度参数;δt为时变的峰度参数。
1.4 模型检验
Kupiec(1995)[9]提出了失败频率检验法,通过观察实际损失超过建立模型后得到的VaR值的概率检验模型的准确性。当实际损失超过模型得到的计算值,标记为预测失败。将置信水平设为τ,选定实际观测天数T,预测失败天数为N,则失败频率为p=N/T。假定模型计算值在时间上是相互独立的,那么预测失败的期望概率为 * 1pτ=-。模型的准确性依赖失败概率p是否等于p*,即检验的零假设是H0:p=p*。
Kupiec提出了对H0的似然比率检验:
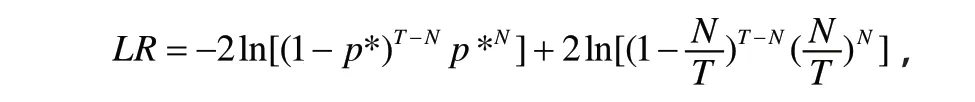
在H0下,LR~。
这种似然比率检验法在评估模型的准确性方面有着广泛的应用,但也存在一定的局限性,当我们基于每日或每周收益率的时间间隔下,导致数据量过少,此时建立的模型很容易低估潜在的损失,导致模型预测失败,因此这种检验方法一般适用有大量观测数据的前提下。
为了进一步验证模型的准确性,本文加入了一个新的评价指标,相对误差率[10]:|,对模型进一步评估。模型效果的优劣可通过相对误差率的大小进行判断,综合两项指标值进行模型筛选,从而建立最优预测模型。
2 基本数据分析
2.1 数据选取
本文选取2009/01/05—2019/12/31的上证指数作为研究对象,其中观测区间为2009/01/05—2018/01/31的2211个值作为训练数据,用于建立模型,观测区间为2018/02/01—2019/12/31的462个观测值作为测试数据,用于模型的综合评价。本文采用对数收益率进行建模,即rt=lnpt-lnpt-1,pt为第t日收盘价。
经检验见(图1)发现,本文选取的收益率序列是平稳的,但不服从正态分布(见图2),并且存在波动聚集和尖峰厚尾的特征(见表2)。

表2 数据基本统计量
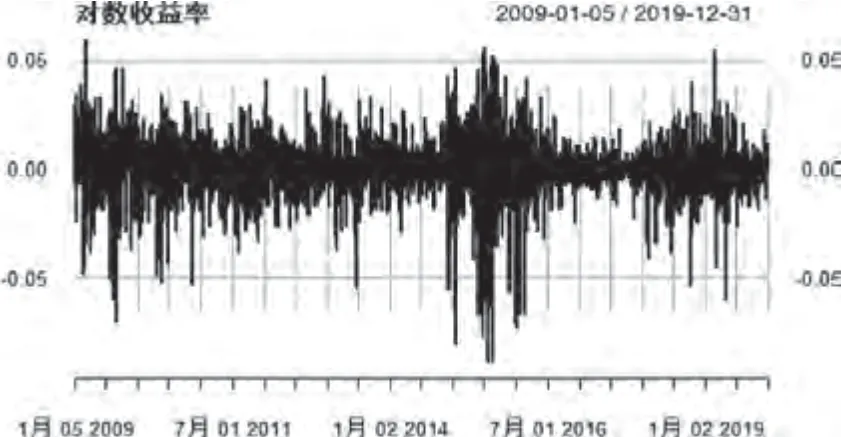
图1 上证指数日对数收益率
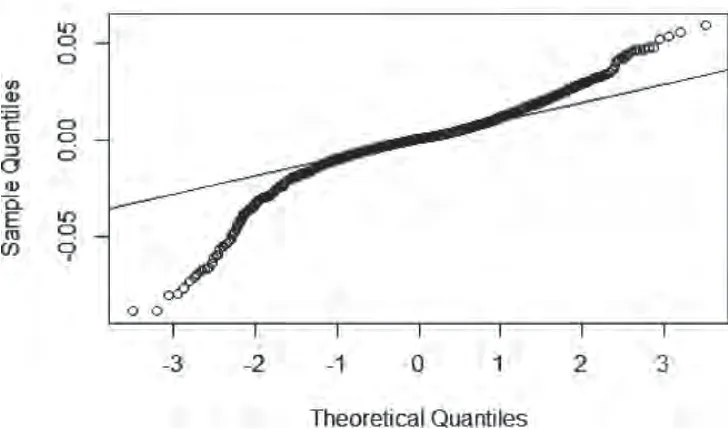
图2 上证指数收益率QQ图
2.2 自相关和偏自相关函数
通过计算上证综合指数收益率及其平方值序列的自相关系数(ACF)和偏自相关系数(PACF),如图3所示。由图3可以看出,上证综指收益率的ACF和PACF基本在临界值范围内,所选取的数据不存在显著的序列相关性,但是从收益率平方的ACF和PACF看出,收益率平方呈现明显的序列相关性。因此,本文研究的收益率序列不存在序列相关,但并不独立,其收益率的条件方差存在序列相关。
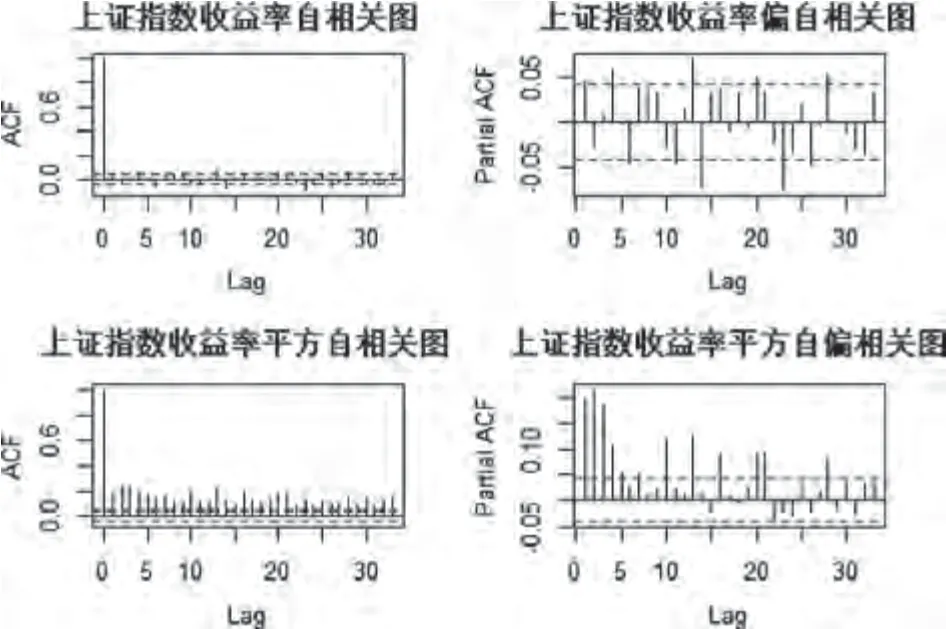
图3 上证指数收益率及其平方的ACF和PACF图
2.3 单位根和平稳性检验
时间序列数据的平稳性是本文对其进行建模的前提。本文使用了三个常用的检验方法,即ADF单位根检验[11]、PP 单位根检验[12]、KPSS平稳性检验[13]。
由表3可以看出,对于(1)(2)序列存在单位根的原假设均被拒绝了,同时KPSS平稳性检验预示着本文的回报序列是平稳的。

表3 平稳性检验
3 模型建立及预测
3.1 估计参数(见表4)及预测结果(见表5)
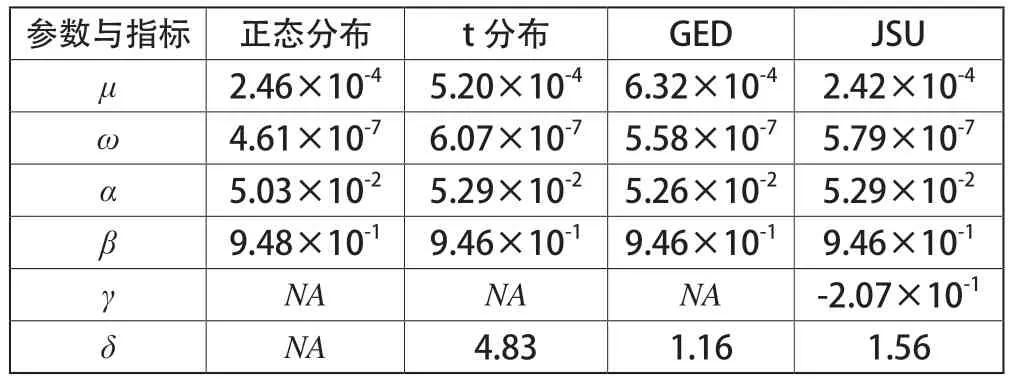
表4 不同分布的参数估计
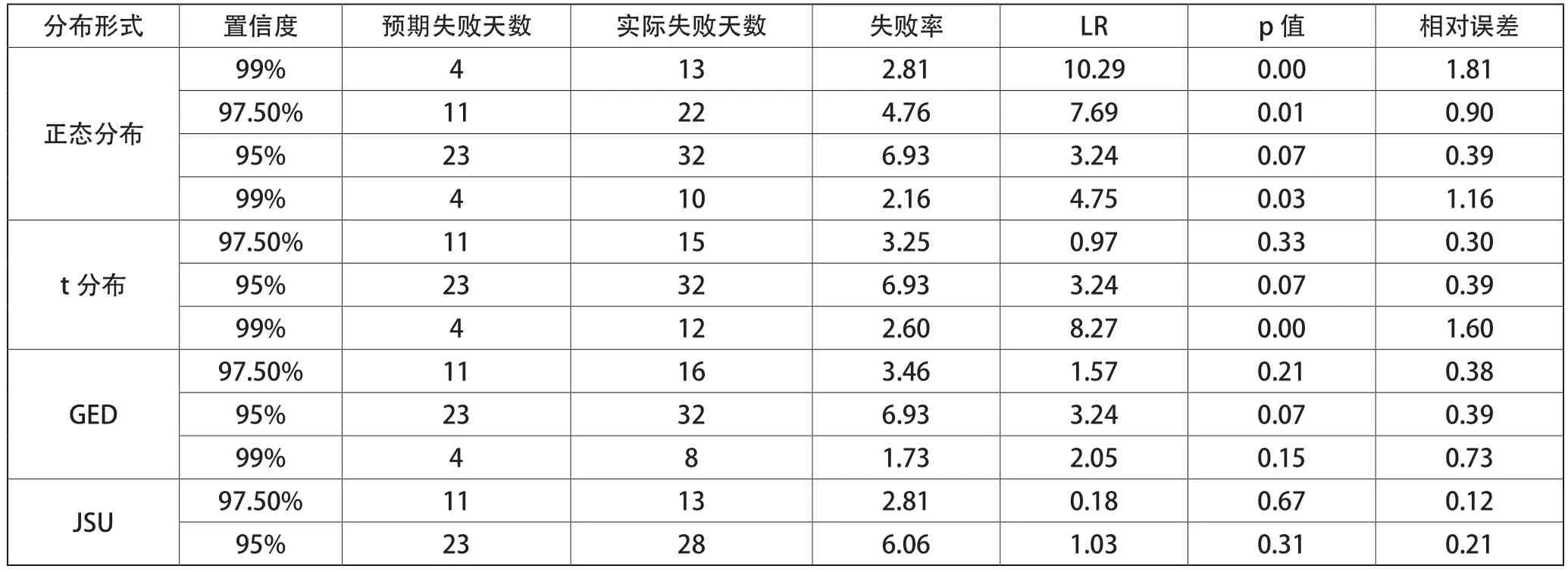
表5 不同分布预测结果
3.2 结果分析
(1)通过Kupiec检验结果来看,99%的置信水平上,正态分布、t分布与GED的p值均有小于5%的显著性水平出现,由此拒绝了Kupiec检验的原假设。
(2)就相对误差来看,JSU分布的相对误差在任意置信水平上均达到最小,说明其预测效果最佳。
因此,在综合两个指标评价后发现,本文提出的JSU模型分布的预测效果是最优的,这种新的分布形式在量化股票风险中表现较好,对投资者和上市企业都是极为有利的。其中,对投资者而言,让其对所选取的目标股票在未来可能发生的风险有一定的认知;对上市企业而言,可以着眼未来可能发生风险的概率,以采取更多的保护措施抵御风险。
但尚有不足之处,第一,本文仅研究了一只股票指数,而金融市场中的产品类型不计其数,因此模型是否具有广泛的说明意义需更多的实证数据来分析,下一步我们将进行此项工作。第二,虽然VaR可以作为机构和投资者在交易时提供一定的信息参考,但金融市场变幻莫测,其结构经常会受到宏观经济政策、国际形势、自然环境等方面的影响,在进行交易时,如果单凭这一个指标是不够的。当前在金融领域,研究人员在不断深入探索新的方法来量化风险,其中包括神经网络、支持向量机等人工智能领域的方法进行结构监测。因此在此领域,未来将考虑结合时间序列和面板数据进行深层次的研究,以建立更为科学合理的风险测量模型。
