攀爬机器人动力学建模与分析
2023-02-16王学军张帆
王学军, 张帆
(昆明理工大学 机电工程学院,云南省先进装备智能制造技术重点实验室,云南省先进装备智能维护工程研究中心,昆明 650500)
采用攀爬机器人代替人工处理发生在人员密集环境下的紧急事故,如火灾,地震,爆炸等,而通常人员密集的地方建筑物比较多,且比较高。因此,研发一种能够在这类环境下攀爬墙面的移动机器人势在必行,该类机器人能够用来完成救援和探测任务[1-2]。为了城市高楼大厦的整洁和美化,通常需要对墙面进行清洁、维护和喷涂,还有一些如管道类狭小空间,用机器人代替工人将会极大的减少人员和财物的安全隐患[3-5]。在以上这两种主要需求的驱动下,各式各样的爬墙类移动设备应运而生,诸如爬墙机器人也是其中一部分。
市面上现有攀爬机器人吸附装置主要分为负压吸附、磁吸附、静电吸附、仿生爪式[6-7]。移动装置主要分为轮式、履带式、轮足混合式。目前市面上的攀爬机器人越障功能不完备,因此如何应对不同墙面上及移动过程中的越障功能是近年来的研究热点[8-10]。对于攀爬机器人来说,建立精准的运动学和动力学模型是完成所有预定目标的基础[11]。Du等[12]基于D-H法在静力系下建立了越障运动学模型。秦基伟等[13]介绍了一种滚动密封式爬壁机器人,分析了其密封与运动机理。提出了一种多履带协调运动的爬壁机器人动力学建模方法,推导出该机器人直线运动及转向动力学方程。徐亚茹和刘荣[14]基于Udwadia-Klaba方程建立了双腔体吸附、轮式移动爬壁机器人的解析动力学模型。Nam等[15]推导出磁吸附柔性多体爬壁机器人的动力学模型。董伟光等[16]基于牛顿-欧拉法对一种可以交叉面过渡的爬壁机器人进行动力学建模,并以运动失效为约束构建不同倾角壁面上的吸附力学模型,但并未考虑机器人关节运动对吸附力影响。以上动力学建模方法中随着广义变量与广义力的增加,计算中包含有大量的微分与偏微分使得算法复杂度较高[17]。
随着机构学和机器人学的发展,挪威数学家Marius Sophus Lie和爱尔兰数学家Ball创立的旋量理论与李群-李代数被应用于运动几何学中。Lee、Wang和Chirikjian[18]运用旋量代数研究串联机构与多肽链。旋量代数和李群、李代数以其对空间直线运动及相关代数运算描述的几何直观性与代数抽象性而成为机器人学研究中重要的数学工具。目前主要运用于工业机器人[19-20]、仿生机器人[21]、医疗康复机器人[22-23]、四面体可展机构[24]、并联机器人[25-26]。
本文设计一种依附于真空吸附的越障攀爬机器人,基于李群李代数与旋量理论建立攀爬机器人的动力学模型,物理意义明确、计算复杂度较低。分别分析攀爬机器人吸附运动与越障运动过程中各关节力学关系,从而寻求攀爬机器人真空吸附产生的吸附力与运动过程中产生的倾覆力矩之间的平衡关系。
1 机构与运动分析
本文所设计的攀爬机器人由两个真空模块与一个越障模块组成:其中真空模块由2自由度的履带移动件与一个真空吸附件组成,越障模块由一个3自由度的机械臂组成,机构原理如图1所示。真空模块中底盘置于真空腔内部,攀爬机器人吸附于墙壁的吸附力通过真空泵抽取真空腔中的空气产生。其中真空腔底面粘贴有密封性好摩擦系数低的材料,以确保攀爬机器人有足够吸附力的情况下可以进行移动。真空模块内部安装有一个2同步带驱动装置,同步带驱动装置由主动同步带轮、从动同步带轮、张紧轮组成,两个同步带驱动装置各自单独驱动。真空模块吸附壁面时,依靠同步带驱动装置可以实现攀爬机器人的直线移动、转向等运动。
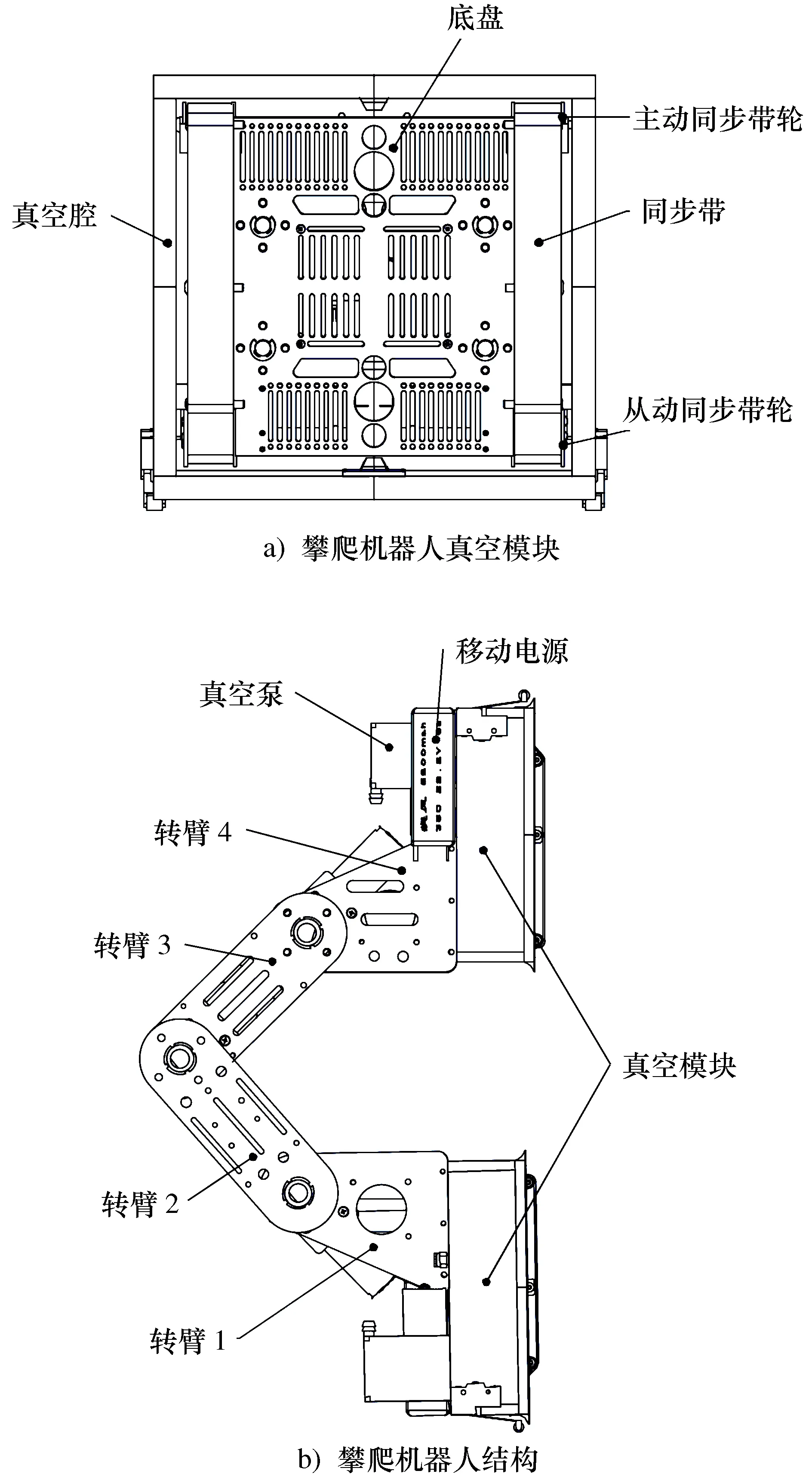
图1 攀爬机器人设计
越障模块由4个转臂通过旋转关节连接,形成一开链三轴机械臂,由3个伺服电机驱动。越障模块两端与两个真空模块连接固接。
根据上述机构分析可知,攀爬机器人运动可分为3种模式:平移吸附运动模式、交替吸附运动模式、越障运动模式。当攀爬机器人在平坦壁面上工作时,采用平移吸附运动,可以发挥其快速灵活的特点;当攀爬机器人在遇到障碍或者过渡墙面的时候,采用越障运动,由一个真空模块吸附壁面作为支撑,越障模块运动越过障碍或者运动至过渡墙面;当攀爬环境较为复杂,无法使用履带移动时,采用交替吸附运动模式,类尺蠖般蠕动,以应对复杂环境。图2为攀爬机器人平移运动模式和越障运动模式下的步态图。

图2 攀爬机器人运动步态
针对攀爬机器人越过直角墙面的步态分析为例解释攀爬机器人运动模块功能:
1) 整个攀爬机器人依靠真空腔产生负压吸附于壁面;
2) 下方真空模块内同步带驱动皮带使真空模块移动靠近上方真空模块,做好越障准备;
3) 上方真空模块断开吸附,越障模块四根转臂配合驱动上方真空模块移动至直角墙面并紧密配合,上方真空模块产生负压吸附直角墙面;
4) 下方真空模块断开吸附,越障模块四根转臂配合驱动下方真空模块移动至直角墙面并紧密配合,下方真空模块产生负压吸附直角墙面,实现直角墙面越障。
2 动力学建模与分析
2.1 空间速度雅可比矩阵
(1)
由式(1)可以看出,攀爬机器人末端的空间速度与其每个关节的速度呈线性关系。记为
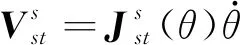
(2)
其雅可比矩阵表示为
以指数积的形式表示空间雅可比矩阵为
gst(θ)=eθ1E1eθ1E2…eθ1Engst(0)
(3)
式中:gst(θ)∈SE(3);Ei表示关节i旋转表示的运动旋量,Ei∈se(3)。
三维欧氏群SE(3)记法为
式中:Z为变换矩阵;R为旋转矩阵;d为平移向量。se(3)为与SE(3)对应的李代数。
可以得到
eθ1E1…eθi-1Ei-1Eieθ1E1…eθi-1Ei-1
(4)
将其改为旋量坐标的形式,即

(5)
式中Ad(*)为李代数的伴随表示。
则雅可比矩阵可写为:

(6)
E′i=Ad(eθ1E1…eθi-1Ei-1)Ei
(7)
根据单位运动旋量坐标的相关定义,与旋转运动副相对应的运动副旋量坐标为
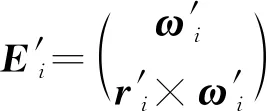
(8)
式中:ω′i为当前位姿下旋转轴线的方向;r′i为当前位姿下轴线上一点的矢量。
ω′i=eθ1[ω1×]eθ2[ω1×]…eθi-1[ω1×]ωi
(9)
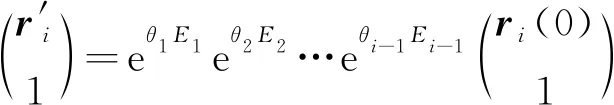
(10)

图3 攀爬机器人机构简图
ω′2=e-[x×]θ1ω2=[I-sinθ1[x×]+(1-cosθ1)×
(11)
式中[x×]为李代数元素。
同理,可得轴3、4的运动方向为:

(12)
轴2、3、4的轴线位置为:
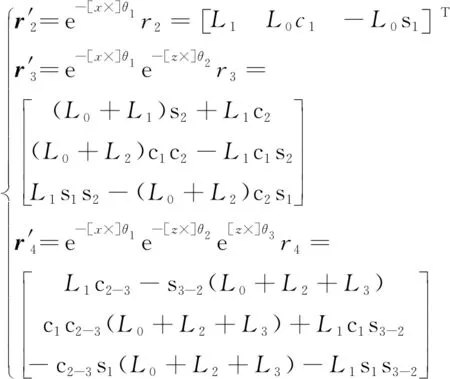
(13)
式中:s1=sinθ1;c2-3=cos(θ2-θ3);s3-2=sin(θ3-θ2)。
攀爬机器人雅可比矩阵为
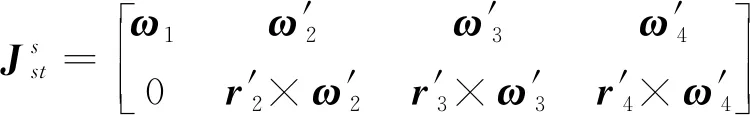
(14)
从以上求解过程中可知,不同于常用的基于D-H坐标法,不需要对运动学正解映射进行求导即可得到攀爬机器人的完整雅可比矩阵形式,利用这种参数化的方法避免了由于奇异性使得攀爬机器人在某些特殊位形或速度取得错误结论。
2.2 动力学模型
通过基于李群李代数的旋量理论对攀爬机器人拉格朗日方程进行了推导,物理意义明确,更加清楚的描述了物体空间运动的力学关系。编程算法中无须再进行求导运算,对于n自由度机器人算法计算效率为O(n)。
为得出拉格朗日动力学模型,基于李群李代数理论中运动旋量的定义写出连杆速度:
(15)

连杆i的质心处的动能为
(16)
式中Mi为连杆i的广义惯性矩阵。
因攀爬机器人势能中仅存在重力势能,因此势能为

(17)
hi为连杆重心高度矩阵。则其拉格朗日函数为

(18)
各关节驱动力矩为
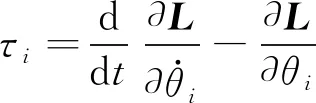
(19)
则得攀爬机器人动力学方程的李群李代数表示为:
(20)
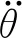
2.3 真空模块力学模型
爬壁机器人吸附力的选择需兼顾真空腔内驱动力、真空腔与壁面摩擦力与越障模块对真空腔造成的倾覆力矩之间的平衡。吸附力过大会造成真空腔与壁面摩擦力过大,无法驱动。吸附力过小会无法承受越障模块对真空腔的倾覆力矩。最佳吸附力定义为防止各种运动失效下的吸附力。
构建真空模块力学模型,利用求解出的动力学方程中机器人关节运动的驱动力矩,构建以各运动失效为条件约束机器人本身关节运动影响下的真空模块力学模型,其中运动失效主要包括机器人掉落、倾覆、打滑、堵转。真空模块受力如图4所示。
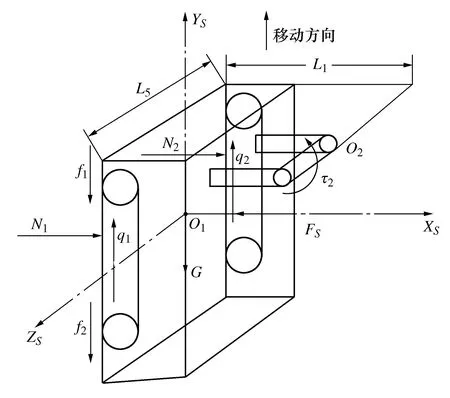
图4 真空模块受力示意图
(21)

为了保证机器人吸附墙面的同时具备移动与越障能力,将其约束条件描述为:
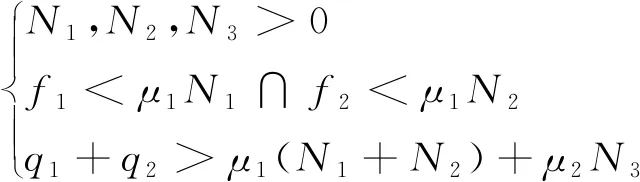
(22)
则可求解得最佳吸附力Fk
Fk=max{Fk1,Fk2,Fk3}
(23)
式中Fki为式(22)中不同约束条件下的吸附力。
3 动力学仿真及实验验证
本文所介绍的爬壁机器人根据结构特性可以进行平面障碍物越障、过渡面越障、交叉面越障、直角面越障,综合越障难度与实际应用,选取直角面越障过程进行分析。利用coppeliasim动力学仿真软件对攀爬机器人进行仿真分析。如图5所示,为获得动力学参数,对攀爬机器人直角墙面越障过程进行动力学仿真。

图5 攀爬机器人仿真模型
为了获得较为精确的结果,在仿真空间中构造一条相同时间间隔路程不同的环形路径路径,选取环形路径中对应的直角面越障中的一段即7~11 s段,通过coppeliasim中inverse kinematics逆运动学求解模块获得7~11 s段匹配直角面越障路径不同的速度与加速度激励,进而获得攀爬机器人各个关节的驱动力矩以验证攀爬机器人动力学模型的准确性。
攀爬机器人结构参数如表1所示,其中转臂1与转臂4、转臂2与转臂3、上下真空腔结构参数完全一致。攀爬机器人各关节旋转速度如图6所示。
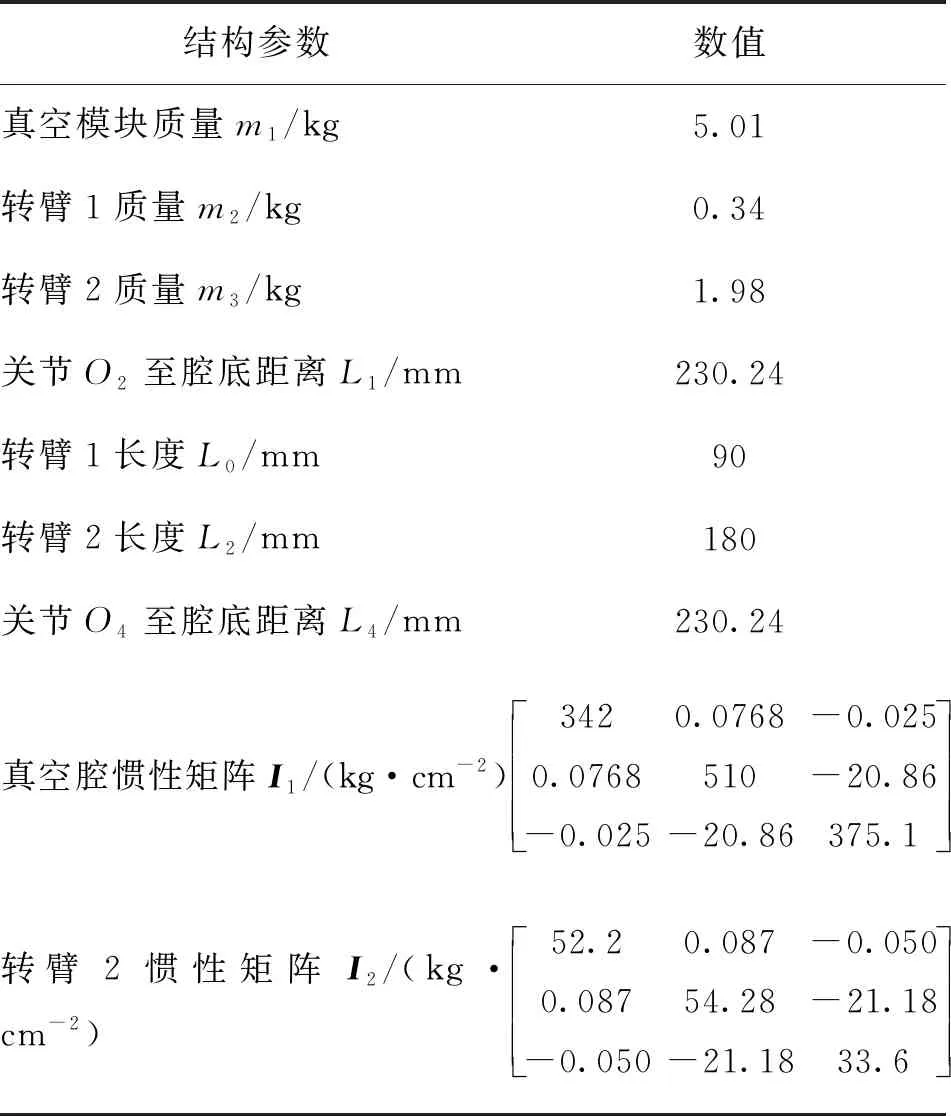
表1 攀爬机器人结构参数

图6 攀爬机器人仿真速度曲线
攀爬机器人各关节仿真驱动力矩如图7所示。为了验证动力学模型(20)准确性,将仿真时采用的角度、速度、加速度激励代入式(20)中,利用MATLAB进行数值计算,将理论力矩与仿真力矩进行对比结果如图8所示。通过图6~图8可以看出前述动力学模型的准确性。
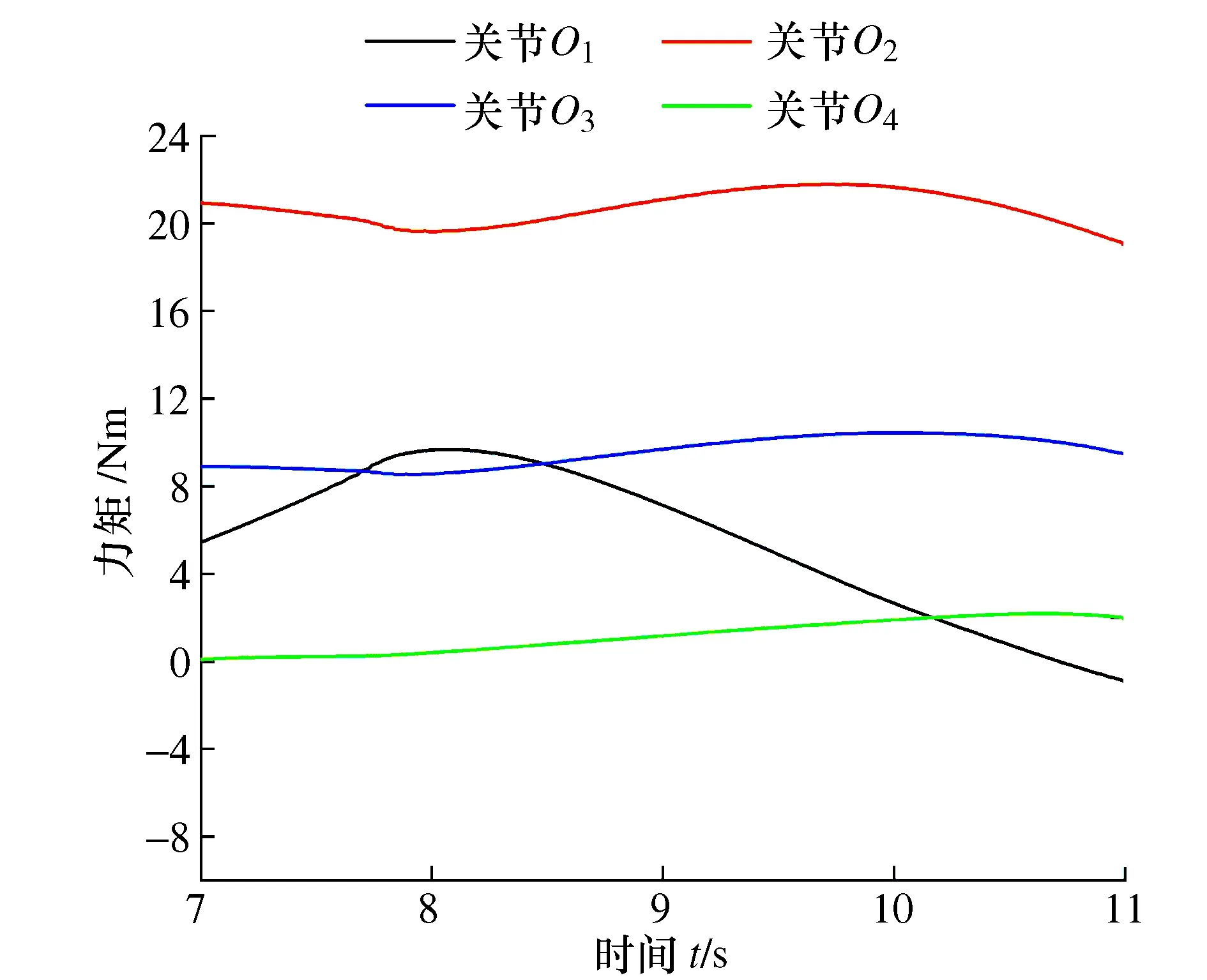
图7 攀爬机器人仿真力矩曲线

图8 仿真与理论结果对比
因为水平平面力系对吸附力影响较小,为简化计算,仅对竖直平面力系影响下的最佳吸附力进行求解。将关节O2运动力矩,通过最小二乘法进行4阶拟合,拟合方程为
τ2=at4+bt3+ct2+dt+e
(24)
式中:a=-0.014 4;b=0.009 1;c=6.549 1;d=-76.704 4;e=268.706 9。
将拟合方程(24)与式(23)联立,得到不同摩擦因数吸附材料在7~11 s的直角面越障运动中随着越障模块各转臂转动角度、角速度、角加速度变化时所需的最佳吸附力如图9所示。
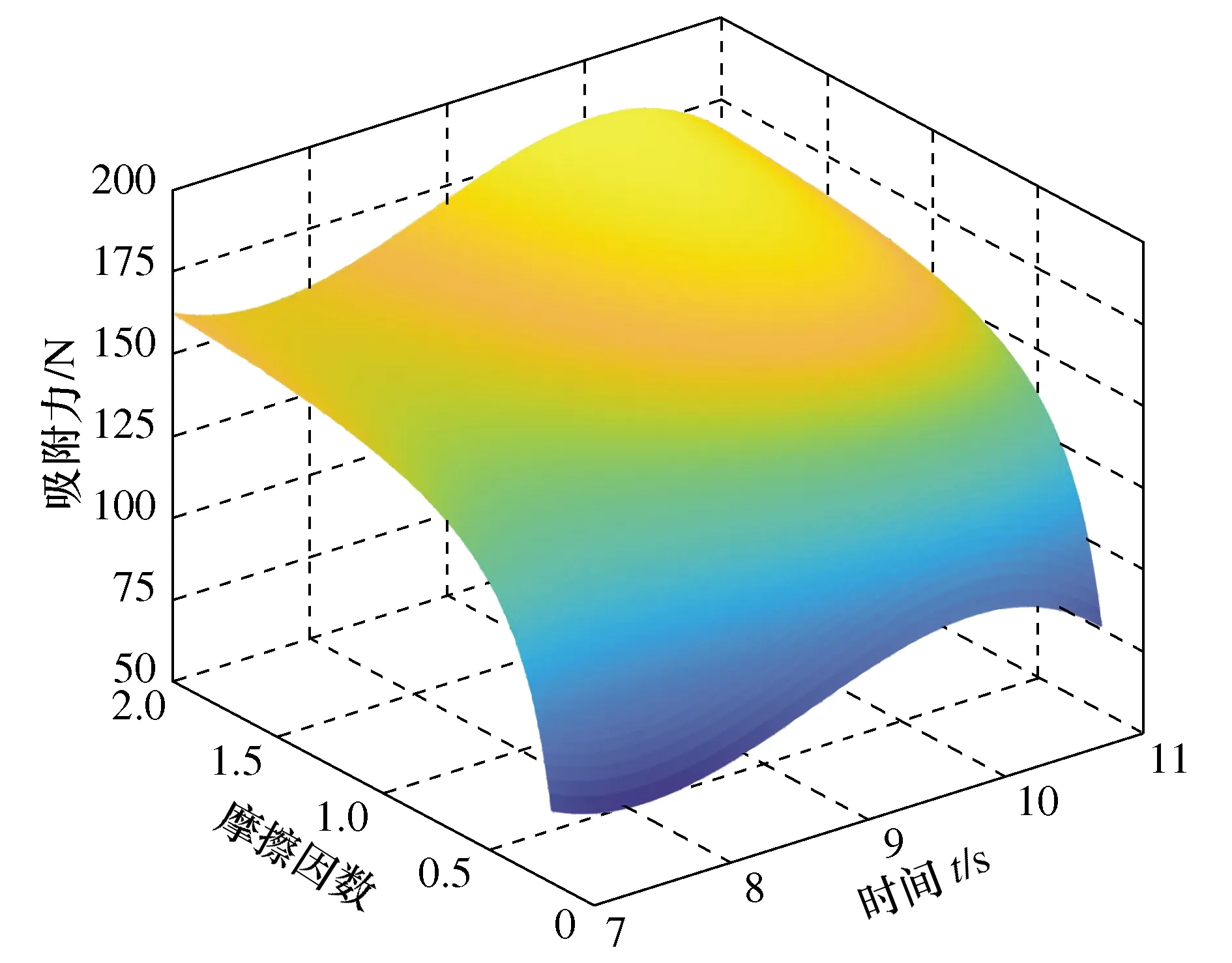
图9 理论最佳吸附力
通过对真空腔体进行吸附实验,如图10所示,验证式(23)求解出的最佳吸附力。

图10 吸附实验
吸附实验结果如表2所示,经过与图9对比,大致与理论符合,试验结果表明真空模块提供的吸附能力可以满足攀爬机器人进行直角面越障。
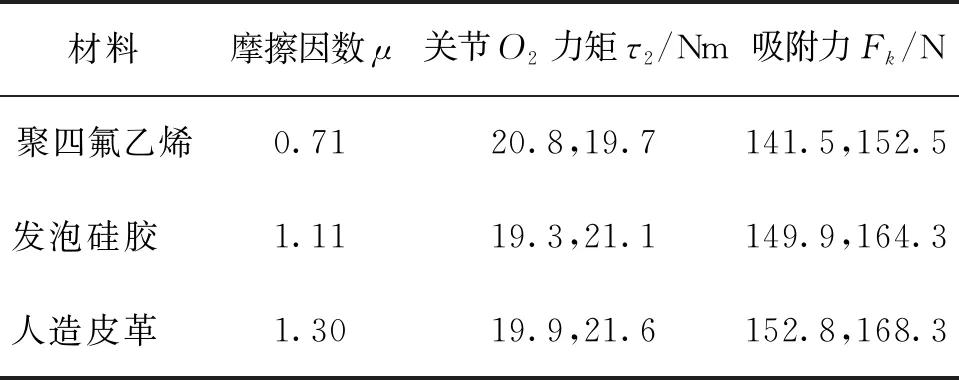
表2 吸附实验数据
4 结论
1) 介绍了一种基于真空吸附的攀爬机器人,该机器人可以进行直角壁面越障。
2) 通过基于李群李代数的旋量理论,从位姿变换的指数积方程入手,推导了攀爬机器人越障过程中空间速度雅可比矩阵,用参数化的方法避免了计算过程中特殊位置奇点。
3) 推导了拉格朗日动力学方程的李群李代数表示形式,物理意义明确,相较传统的建模方法计算复杂度由O(n4)降为O(n)。并通过仿真验证了李群李代数法建立动力学模型的正确性。
4) 建立真空模块力学模型,求解在关节越障运动下为防止运动失效,真空腔所需最佳吸附力,并通过实验进行验证。
