复合势下三维旋量玻色-爱因斯坦凝聚暗孤子及其自旋纹理*
2017-09-08王海红宗丰德
王海红, 宗丰德
(浙江师范大学 非线性物理研究所,浙江 金华 321004)
复合势下三维旋量玻色-爱因斯坦凝聚暗孤子及其自旋纹理*
王海红, 宗丰德
(浙江师范大学 非线性物理研究所,浙江 金华 321004)
为了充分揭示复合势下三维旋量玻色-爱因斯坦凝聚暗孤子的动力学性质及自旋纹理结构,运用能量泛函方法和直接数值仿真耦合Gross-Pitaevskii方程组,在三维抛物势和二维高斯势组成的复合势下构造了多种带有不同拓扑结构因子稳定的自旋为1的三维铁磁态旋量玻色-爱因斯坦凝聚暗孤子,并分析了它们的动力学特性.选择其中一种暗孤子作为例子,分析了其在关键参量空间中的稳定性,得到了稳定性区域.然后通过计算暗孤子的自旋密度矢量,得到了指向自旋消失圆的三维环形自旋纹理结构和自旋密度矢量大小随空间变化的分布.这为更好地理解玻色-爱因斯坦凝聚的磁性性质提供了帮助,也为实验上实现三维旋量玻色-爱因斯坦凝聚暗孤子提供了理论依据.
旋量玻色-爱因斯坦凝聚;耦合Gross-Pitaevskii方程组;暗孤子;自旋纹理
0 引 言
作为物质波孤子的一种,暗孤子一直以来都备受研究者的亲睐,尤其在玻色-爱因斯坦凝聚的研究中,理论和实验都有了很大的进展,得到了产生暗孤子的多种方法,如相位植入法[1]、密度调制法[2]及超音速流法[3]等,同时对多种结构的暗孤子及其动力学进行了深入的研究[4-7].随着光阱技术的发展,对玻色-爱因斯坦凝聚的研究达到了一个新的高度,在全光阱下,原子的自旋自由度得到了保护,形成了旋量玻色-爱因斯坦凝聚[8],这为研究凝聚体中的暗孤子增添了更多的可能性.Song 等[9]通过数值模拟相位植入的方法,在F=1的玻色-爱因斯坦凝聚中研究了二维环形暗孤子结构.Nistazakis等[10]研究了自旋为1的一维旋量玻色-爱因斯坦凝聚中的暗-暗-亮和亮-亮-暗复合矢量孤子的产生,并在平均场理论下,分析了复合孤子的动力学特征.接着,Xiong等[11]在局域磁场下,通过求解耦合的Gross-Pitaevskii(GP)方程组,探讨了旋量玻色-爱因斯坦凝聚中矢量孤子的构建,并数值验证了其稳定性.同时,对于旋量玻色-爱因斯坦凝聚,原子自旋所表现出的性质,譬如自旋纹理,也吸引了许多学者的注意.Mueller[12]研究了缓慢旋转下自旋为1的玻色-爱因斯坦凝聚中斯格明子纹理的2种类型;Pogosov等[13]探讨了二维抛物势下自旋为2的涡旋结构及其对应的自旋纹理.最近,Kunimi[14]在准一维旋转环势阱下,研究了自旋为1的玻色-爱因斯坦凝聚体中自旋纹理的亚稳定性.旋量玻色-爱因斯坦凝聚暗孤子及由自旋相互作用产生的自旋纹理、自旋畴等一系列拓扑现象的研究对实现量子信息的储存和处理起到一定的推进作用,也为更好地理解玻色-爱因斯坦凝聚体的磁性提供了帮助.然而,由外势构造的旋量玻色-爱因斯坦凝聚三维暗-暗-暗矢量孤子及其暗孤子的自旋纹理还鲜有报道.
因此,本文研究由三维复合势构造的旋量玻色-爱因斯坦凝聚暗孤子及其自旋纹理.首先,运用能量泛函的方法[15],得到多种带有不同拓扑结构因子组合的暗孤子;接着,通过直接数值仿真耦合的GP方程组,分析这些暗孤子的动力学特征,并对其中一种暗孤子进行大量数值计算,得到其在关键参量中的稳定性区域.最后,通过计算暗孤子的自旋密度矢量,得到了指向自旋消失圆的三维环形自旋纹理结构,并通过计算自旋密度矢量大小随空间变化的分布,更清楚地显示了自旋纹理的分布.
1 理论模型和能量泛函
在平均场近似下,三维旋量玻色-爱因斯坦凝聚系统的动力学特性可以由下面的耦合GP方程组描述[9,16]:
(1)

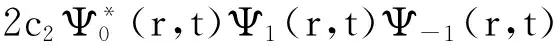
(2)
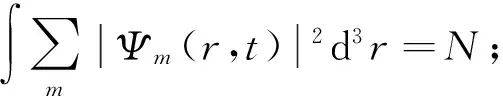
(3)
式(3)中:ω⊥,ωz,P0及a分别表示抛物势的径向振动角频率、z轴方向的振动角频率、高斯势的强度及脉冲宽度.下文的研究表明,高斯势的强度P0和其脉冲宽度a对旋量玻色-爱因斯坦凝聚暗孤子的稳定性具有十分重要的影响.
旋量玻色-爱因斯坦凝聚波函数对应的静态解Φm(r)可以通过将
(4)
代入方程组(1)~(2)中得到.此时,系统的能量泛函为
(5)
(6)
(7)
(8)
为了得到无量纲化耦合GP方程组(6)与(7)的静态解,考虑到复合外势的柱对称性分布,笔者提出如下形式的静态旋量玻色-爱因斯坦凝聚暗孤子试探波函数:
(9)
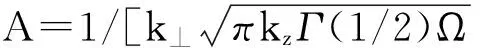
(10)
本文取ξ1=1,ξ0=0,ξ-1=-1;θ1=1,θ0=0,θ-1=-1.
2 旋量玻色-爱因斯坦凝聚暗孤子的动力学分析


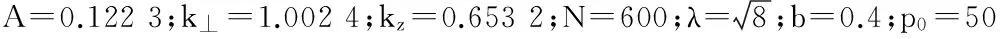
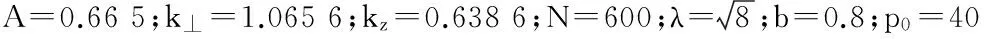
图1 三维旋量玻色-爱因斯坦凝聚暗孤子等值面图
接着,将所得的旋量玻色-爱因斯坦凝聚暗孤子最优化静态解形式作为对耦合GP方程组进行数值仿真时的初态,运用Crank-Nicholson算法[23]数值仿真方程组(6)~(7),分析暗孤子的动力学演化特性.考虑到计算机集群计算容量的限制,时间和空间步长分别取0.001和0.045,网格大小为256×256×256,即三维空间范围为-5.76≤x,y,z≤5.76.图2和图3分别给出了(3,2,1)暗孤子和(4,3,2)暗孤子在x=0平面从t=0到t=100的稳定演化图及初态、末态和将初态加10%微扰演化的末态的一维振幅图,从图中可以看出,所得到的暗孤子是稳定的.

图2 (3,2,1)暗孤子在x=0平面从t=0到t=100的稳定演化图及旋量暗孤子的 一维振幅图(实线为初态,点线为末态,虚线为加10%微扰后得到的末态)
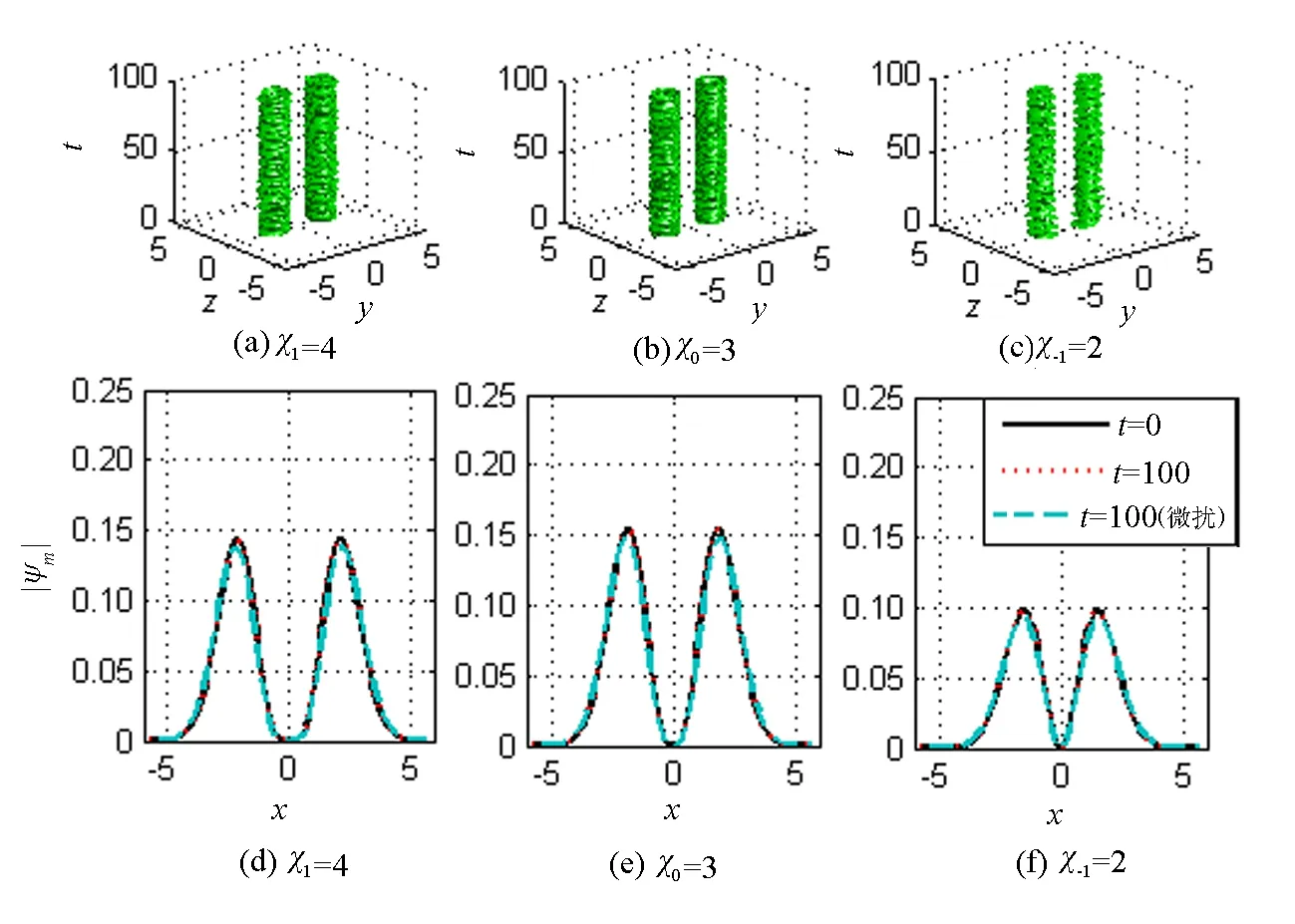
图3 (4,3,2)暗孤子在x=0平面从t=0到t=100的稳定演化图及旋量暗孤子的 一维振幅图(实线为初态,点线为末态,虚线为加10%微扰后得到的末态)
随后,笔者选取旋量玻色-爱因斯坦凝聚(4,3,2)暗孤子,对其进行大量的数值计算,得到对应的暗孤子在重要参量(p0,b)空间的稳定区域,其曲线是临界曲线,如图4所示.临界曲线上方为稳定区域,下方为不稳定区域.由此可以得出,复合外势中的高斯势的较小强度和较大脉冲宽度更有利于所选的旋量玻色-爱因斯坦凝聚暗孤子的稳定性,这为旋量玻色-爱因斯坦凝聚暗孤子的实验提供了思路,希望此实验尽快实现.需要指出的是,对于不同组拓扑结构因子构成的暗孤子,存在不同的稳定区域.
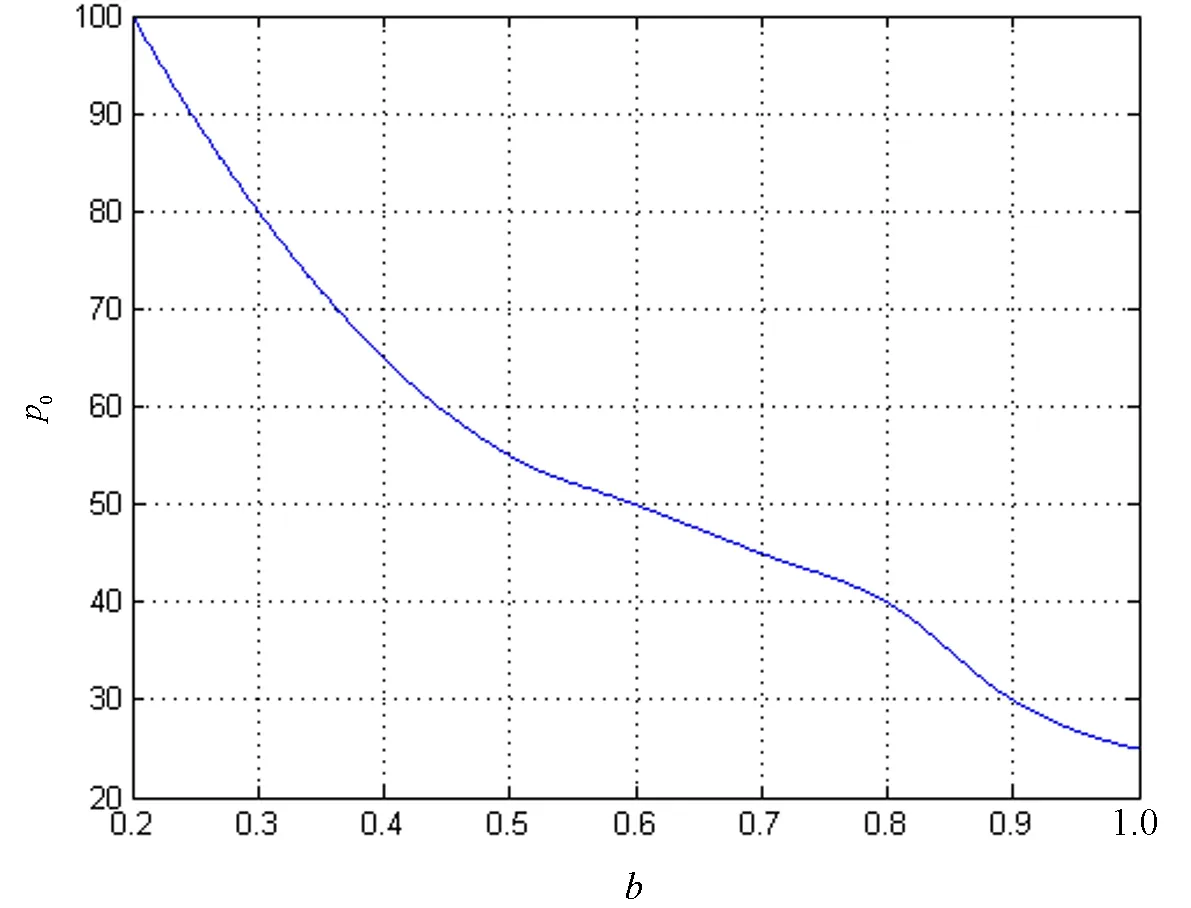
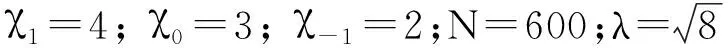
图4 三维旋量玻色-爱因斯坦凝聚暗孤子在参量(p0,b)上的稳定区域图
3 旋量玻色-爱因斯坦凝聚暗孤子的自旋纹理
(11)

(12)
图5描述了带有(3,2,1)拓扑结构因子的旋量玻色-爱因斯坦凝聚暗孤子的自旋纹理.从图5(a)可看出,在平面z=0两侧自旋方向相反,即在平面z=0上方,自旋方向向下;而在平面z=0下方,自旋方向向上.图5(b)显示了在z=0平面上指向自旋消失圆的自旋纹理.结合图5(a),(b)可知,旋量玻色-爱因斯坦凝聚暗孤子的自旋纹理结构为指向自旋消失圆的三维环形结构.为更清楚地显现出自旋纹理强度的空间分布,笔者计算了自旋密度矢量大小随空间的变化情况,图5(c),(d)分别为自旋密度矢量大小随空间变化的强度在y=0,z=0的切片图.类似地,图6给出了带有(4,3,2)拓扑结构因子的旋量玻色-爱因斯坦凝聚暗孤子的自旋纹理,相比于图5,三维环形自旋纹理结构的内部较大,这与拓扑结构因子的大小相关,即不同拓扑结构因子组合所对应的暗孤子的自旋纹理结构相似.随着拓扑结构因子的增大,环形内部也相应变大.
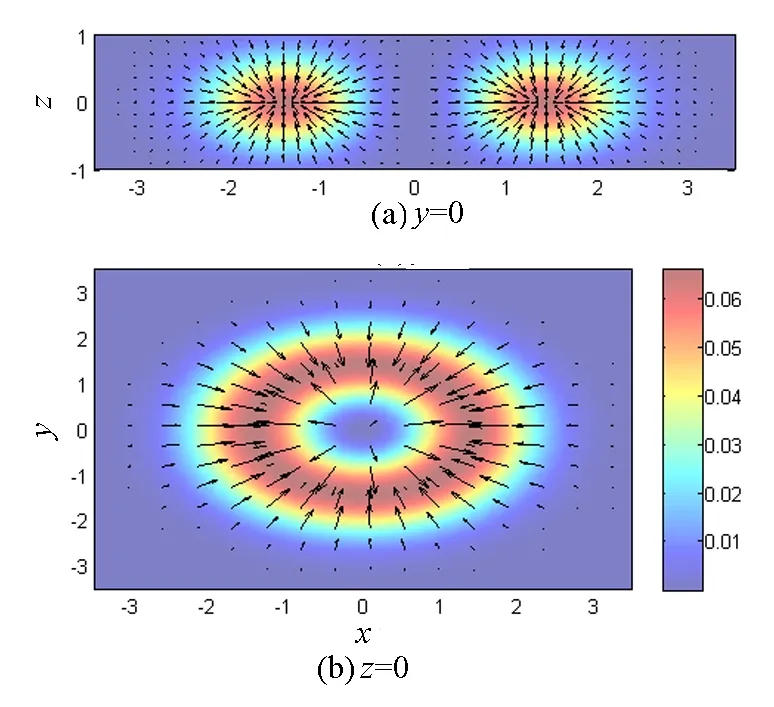
(c),(d)分别为自旋密度矢量大小随空间变化分布的切片图(参数同图2)
图5 (3,2,1)旋量暗孤子的自旋纹理的切片图
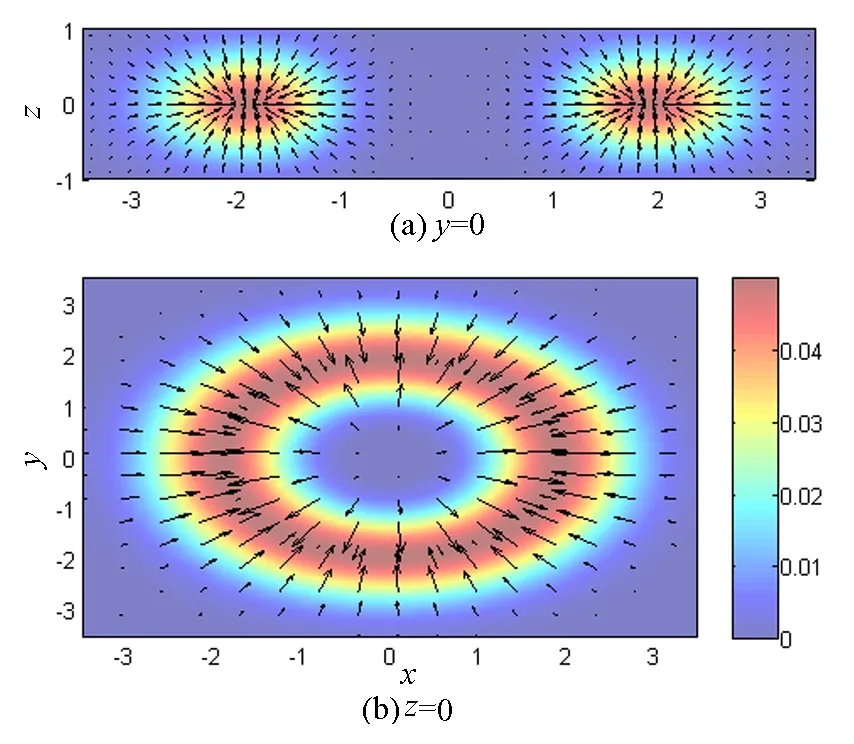
(c),(d)分别为自旋密度矢量大小随空间变化分布的切片图(参数同图2)
图6 (4,3,2)旋量暗孤子的自旋纹理的切片图
4 结 语
在自旋为1的铁磁态旋量玻色-爱因斯坦凝聚中,通过由三维抛物势和沿径向的二维高斯势组成的复合外势构造了带有不同拓扑结构因子组的三维暗孤子,并分析了其动力学特性及其在重要参量(p0,b)空间的稳定性,得到了稳定的旋量玻色-爱因斯坦凝聚暗孤子.同时,通过计算旋量玻色-爱因斯坦凝聚暗孤子的自旋密度矢量,得到了指向自旋消失圆的三维环形自旋纹理和自旋纹理强度随空间变化的分布,这就更清晰地反映了旋量玻色-爱因斯坦凝聚暗孤子自旋纹理的分布结构.这将为更好地理解玻色-爱因斯坦凝聚的磁性性质提供帮助,也为实验上实现三维旋量玻色-爱因斯坦凝聚暗孤子提供一定的理论指导.
[1]Burger S,Bongs K,Dettmer S,et al.Dark solitons in Bose-Einstein condensates[J].Phys Rev Lett,1999,83(25):5198-5201.
[2]Anderson B P,Haljan P C,Regal C A,et al.Watching dark solitons decay into vortex rings in a Bose-Einstein condensate[J].Phys Rev Lett,2001,86(14):2926-2929.
[3]Ei G A,Gammal A,Kamchatnov A M.Oblique dark solitons in supersonic flow of a Bose-Einstein condensate[J].Phys Rev Lett,2006,97(18):180405.
[4]Busch T,Anglin J R.Motion of dark solitons in trapped Bose-Einstein condensates[J].Phys Rev Lett,2000,84(11):2298-2301.
[5]Theocharis G,Frantzeskakis D J,Kevrekidis P G,et al.Ring dark solitons and vortex necklaces in Bose-Einstein condensates[J].Phys Rev Lett,2003,90(12):120403.
[6]Bilas N,Pavloff N.Propagation of a dark soliton in a disordered Bose-Einstein condensate[J].Phys Rev Lett,2005,95(13):130403.
[7]Wang W,Kevrekidis P G,Carretero-Gonzalez R,et al.Dark spherical shell solitons in three-dimensional Bose-Einstein condensates:existence,stability,and dynamics[J].Phys Rev A,2016,93(2):023630.
[8]Barrett M D,Sauer J A,Chapman M S.All-optical formation of an atomic Bose-Einstein condensate [J].Phys Rev Lett,2001,87(1):010404.
[9]Song S W,Wang D S,Wang H Q,et al.Generation of ring dark solitons by phase engineering and their oscillations in spin-1 Bose-Einstein condensates[J].Phys Rev A,2012,85(6):063617.
[10]Nistazakis H E,Frantzeskakis D G,Kevrekidis P G,et al.Bright-dark soliton complexes in spinor Bose-Einstein condensates[J].Phys Rev A,2008,77(3):033612.
[11]Xiong B,Gong J B.Dynamical creation of complex vector solitons in spinor Bose-Einstein condensates[J].Phys Rev A,2010,81(3):033618.
[12]Mueller E J.Spin textures in slowly rotating Bose-Einstein condensates[J].Phys Rev A,2004,69(3):033606.
[13]Pogosov W V,Kawate R,Mizushima T,et al.Vortex structure in spinorF=2 Bose-Einstein condensates[J].Phys Rev A,2005,72(6): 063605.
[14] Kunimi M.Metastable spin textures and Nambu-Goldstone modes of a ferromagnetic spin-1 Bose-Einstein condensate confined in a ring trap[J].Phys Rev A,2014,90(6):063632.
[15]徐志君,施建青,林国成.轴对称谐振势阱中玻色凝聚气体基态和单涡旋态解[J].物理学报,2007,56(2):666-672.
[16]Ho T L.Spinor Bose condensates in optical traps[J].Phys Rev Lett,1998,81(4):742-745.
[17]Fatemi F K,Jones K M,Lett P D.Observation of optically induced Feshbach resonances in collisions of cold atoms[J].Phys Rev Lett,2000,85(21):4462-4465.
[18]Bergeman T,Moore M G,Olshanii M.Atom-atom scattering under cylindrical harmonic confinement:numerical and analytic studies of the confinement induced resonance[J].Phys Rev Lett,2003,91(16):163201.
[19]Van-Kempen E G M,Kokkelmans S J J M F,Heinzen D G,et al.Interisotope determination of ultracold Rubidium interactions from three high-precision experiments[J].Phys Rev Lett,2002,88(9):093201.
[20]Tomoya I,Kazushige M.Axisymmetric vortices in spinor Bose-Einstein condensates under rotation[J].Phys Rev A,2002,66(2):023602.
[21]Pietilä V,Möttönen M,Virtanen S M M.Stability of coreless vortices in ferromagnetic spinor Bose-Einstein condensates[J].Phys Rev A,2007,76(2):023610.
[22]Wang Y C,Lv J,Zhu L,et al.Crystal structure prediction via particle-swarm optimization[J].Phys Rev B,2010,82(9):094116.
[23]Muruganandam P,Adhikari S K.Fortran programs for the time-dependent Gross-Pitaevskii equation in a fully anisotropic trap[J].Comput Phys Commu,2009,180(10):1888-1912.
Three-dimensional spinor Bose-Einstein condensate dark-solitons and its spin texture under a complex potential
WANG Haihong, ZONG Fengde
(InstituteofNonlinearPhysics,ZhejiangNormalUniversity,Jinhua321004,China)
In order to fully reveal the dynamic properties and the spin texture distribution of three-dimensional spinor Bose-Einstein condensate dark-solitons under a complex potential, it was constructed a stable spin-1 ferromagnetic three-dimensional spinor Bose-Einstein condensate dark-solitons with the different topological structure factors confined a complex potential including a three-dimensional harmonic trap and a two-dimensional Gaussian trap, via employing the energy functional method and direct numerical simulation of the coupled Gross-Pitaevskii equations, their dynamics were analyzed. In addition, it was obtained the stability region of the one of these in important parameter space. Furthermore, it was also obtained the cricoid spin texture structure pointing to the circle of spin vanishing by calculating the spin density vector of the dark-solitons. With the purpose of more clearly described the spin texture distribution, it was calculated the variational intensity of spin density vector size along with the space. These results could help people better understand the magnetism of the spinor Bose-Einstein condensate and provide the theory for the relational experimental research.
spinor Bose-Einstein condensate; coupled Gross-Pitaevskii equations; dark soliton; spin texture
10.16218/j.issn.1001-5051.2017.03.006
�2017-02-28;
2017-03-31
国家自然科学基金资助项目(11072219);浙江省自然科学基金资助项目(Y1080959)
王海红(1991-),女,山西晋中人,硕士研究生.研究方向:玻色-爱因斯坦凝聚.
宗丰德.E-mail: fdzong@zjnu.cn>
O415
A
1001-5051(2017)03-0281-08
