轴承间隙对轴承振动影响的理论模型与试验研究
2023-02-16汪凯江胜飞胡波张晓东
汪凯, 江胜飞, 胡波, 张晓东
(1. 成都理工大学 机电工程学院,成都 610059; 2. 中石油西南油气田分公司,四川泸州 646000;3. 西南石油大学 机电工程学院,成都 610500)
目前,基于振动信号的轴承故障监测都是从信号处理的角度进行研究,而没有结合到轴承振动的动力学特性。本研究从正常轴承的振动特性入手,旨在进一步验证轴承间隙对轴承振动的影响。Tallian和Gustafsson[1]首先提出了轴承内间隙对振动的影响,仿真结果说明了轴承间隙越大,轴承振动的振幅也越大。文献[2-3]基于赫兹接触理论提出了非线性3-DOF模型,通过数值仿真实验证实了增大预紧力或者增加滚动体的数量或者两者都增加会减小振动幅值。文献[4-5]同样基于赫兹接触理论通过非线性模型对混沌运动进行了研究分析,数值仿真结果证实了转子滚动轴承系统会有谐波、超谐波、亚谐波、振动以及混沌振荡现象。陈予怒院士为了深刻揭示球轴承-转子系统的共振机理,首次应用平均法求得了系统在主共振情况下的解析解,并讨论了系统参数对主共振的影响[6-7]。郭瑞、赵国瑶等基于轴承间隙内润滑油的流动特点,提出了流场中存在动压-空化耦合关系,并结合气液混合相模型及全空化模型对间隙内三维流场进行数值求解[8]。魏维等以轴承间隙为设计变量,分析轴承间隙对动态特性系数的影响,研究结果表明,增大轴承间隙会降低系统的稳定性[9-10]。
综合文献调研,只有极少数的文献是基于对轴承振动模型的研究,同时各种振动的分类与轴承参数之间的可能关系也没有进行研究分析。本研究将结合振动信号与轴承振动的动力学特性对2-DOF非线性模型进行研究分析,明确轴承振动不同类型的分类以及轴承间隙对振动信号的影响。
1 系统模型的建立
将轴承支撑的旋转机械简化成由转盘、旋转轴以及轴对称分布的弹簧和阻尼器代表的两柔性轴承构成的系统模型,如图1所示。

图1 两轴承支撑的转子系统
由滚动轴承支撑的旋转系统,几乎没有滚动体承受动载荷,同时承载区域的弹性变形提供系统刚度。当机械在低速旋转时,惯性力和粘滞阻尼都可忽略不计,且加载在系统上的主动力就是转子静态时的重量。当机械在高速旋转时,转子的惯性力和粘滞阻尼会影响轴承外圈在轴向和径向上的运动,并产生非线性、耦合的变刚度。
为了研究转子系统中滚动轴承的动力学特性,在质量、弹簧、阻尼系统中将转子的质量集中于内圈中心,同时由一组等同并行的非线性弹簧支撑该系统。该2-DOF模型如图2所示,相对于转子来说,该系统忽略了滚动体的惯性,同时承载区域内滚动体所受的合力为激振力。
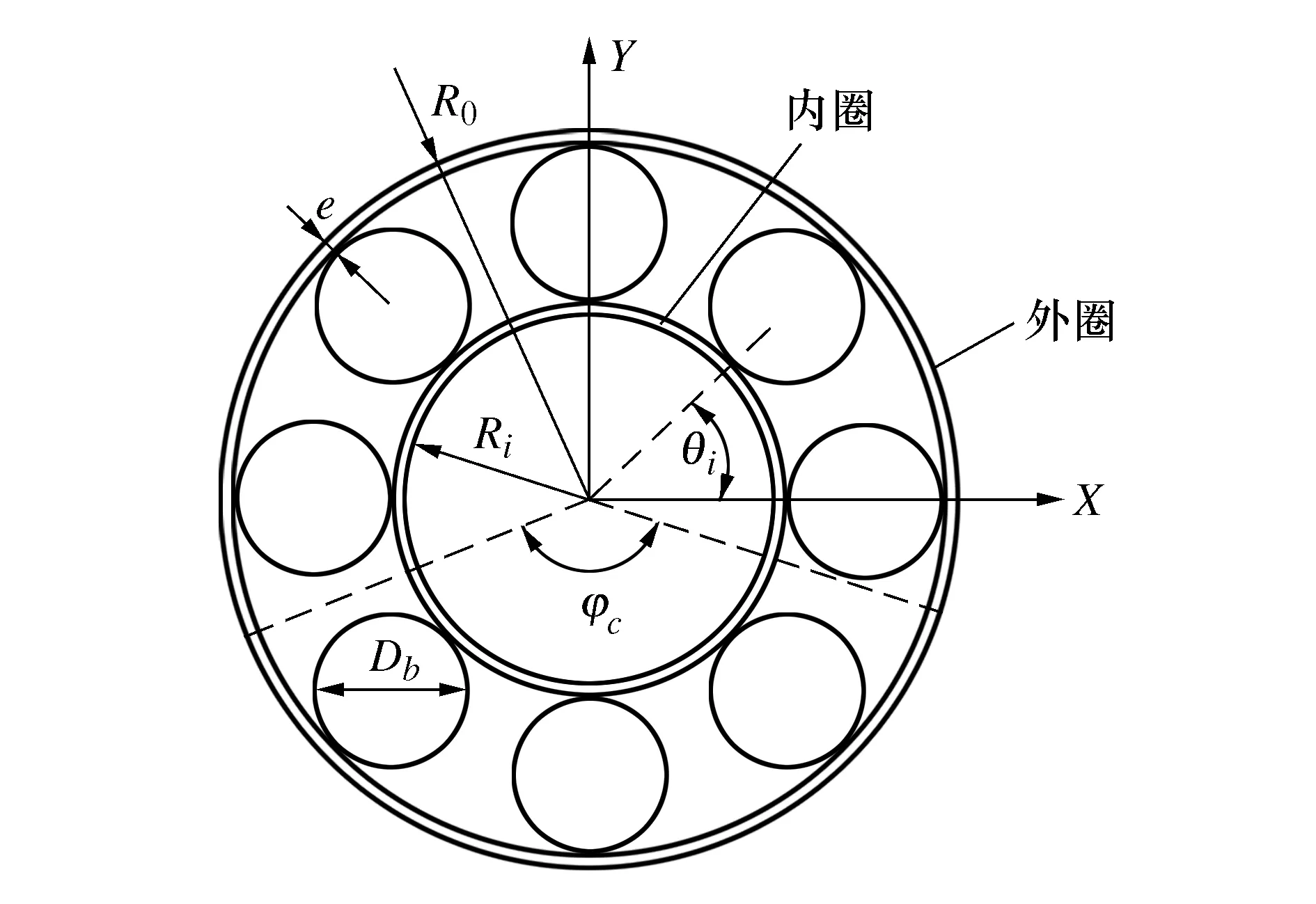
图2 2-DOF滚动轴承的模型
针对2-DOF滚动轴承的模型,做以下假设:
1) 轴处于内圈的中心位置,且外圈是静止的;
2) 整个系统的外力只有转子的重力,且假设滚道是无故障的;
3) 轴承的几何参数如下,内外圈的半径分别为Ri和R0,轴承内间隙为e,滚珠直径为Db,而且在整个过程中Db是恒定不变的。
模型中,滚动体均布在转子上,且第i个滚动体的位置角度θi为
(1)
式中:N为滚动体的总数目;ω为内圈的转速,且与主轴转速ωs成正比。
(2)
由于内圈的位置变化,会产生小的变形量δi,且施加于每个滚动体上。
这些径向变形量可根据图3的几何模型上滚动体的位置角度θi、内圈的坐标(x,y)及间隙e计算出来。
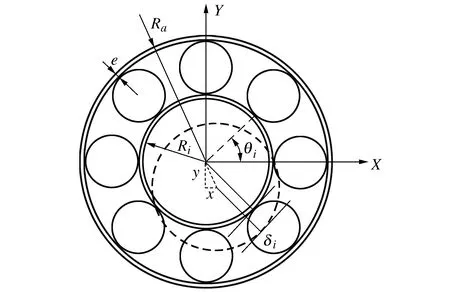
图3 径向变形量计算模型
得出径向变形量为
δi=xcosθi+ysinθi-e
(3)
将式(1)代入式(3),得到径向变形量为
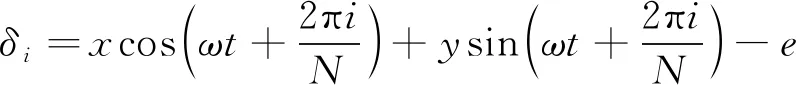
(4)
回复力Fi与承载区域的每个滚动体都有关联,通过赫兹接触理论可以得到

(5)
式中:k为接触刚度;权重n的取值取决于滚动体的形状。
根据外载荷与滚动体的承载平衡关系,可得:

(6)
在式(6)中,当单位阶跃函数(x>0,H(x)>0;x≤0,H(x)=0)大于零时,承载区域内的相关滚珠就会受压且压力施加在内圈上。因此,转子轴承系统的运动控制方程可表示为:
(7)
式中Nc表示承载区域内滚动体的个数。
为了求解式(7),承载区域内滚动体的个数Nc和转子平衡点的位置由承载区域内滚动体回复力的泰勒级数展开式分析得到,式(7)就转化成一组包含周期系数的非线性常微分方程组。这样,系统方程的闭合解就可以通过广义积分变换法求解。
2 载荷分布角的研究
在滚动轴承中,通过滚动体将载荷传递到内外圈上,径向力连续分布在内圈与外圈之间受压的滚动体上。
载荷分布角如图4所示。
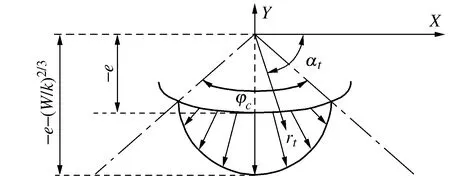
图4 载荷分布角
因此,转子的径向变形量仅仅存在于承载区的滚动体上,可表示为:
(8)
通过极坐标转换,x=rtcosαt,y=rtsinαt,以内圈中心为坐标原点,可表示为:
(9)
(10)
当单个滚动体支撑起整个转子的重量时,此时rt出现最大值。在这种准静态条件下(ω≈0),依据赫兹接触理论和式(9)及式(10),可以推导出载荷分布角的表达式为
(11)
因此,带扰动项的承载区内滚动体数目的计算公式就可以推导出来,可表示为
(12)
承载区域内滚动体的数目主要取决于轴承内间隙和径向力。此外,承载区域内滚动体的位置和数目会随着时间的变化而不断改变,因此系统刚度对承载区域内滚动体的数目有决定性的作用,这也是系统振动和系统时变性的潜在因素。
3 平衡点分析
将轴的平衡点标记为(x,y),基于公式(7)将任一点对时间求导(xe,ye)=0。因此,在无故障滚动轴承上施加一个理论上完全平衡的转子,平衡点则满足以下方程组。
(13)
平衡点的位置取决于轴承间隙、径向力以及承载区域内的滚动体的数目。通过数值求解公式(13)可以得到系统的平衡点。当轴承内间隙为0时(e=0),承载区域内滚动体的数目达到最大值Nc=N/2。在准静态条件下(ω≈0),公式(13)通过极坐标转换xe=recosφe,ye=resinφe得到:
(14)

(15)
对于内间隙为零的轴承的平衡点方程可以表示为
(xe,ye)|e=0=[0,-(4W/Nk)2/3]
(16)
为了研究轴承内间隙对平衡点位置的影响,将∅127涡轮钻具轴承的数据代入公式(13)进行数值求解分析,∅127涡轮钻具轴承的具体参数见表1。

表1 ∅127涡轮钻具轴承的具体参数
通过公式求解,当内间隙e<4.5 μm时,内环承载区有3~4个滚动体,此时有且仅有一个平衡点;当内间隙e>4.5 μm时,可能会有3个平衡点。平衡点的稳定性可以通过转子系统在平衡点(xe,ye)处雅可比矩阵的特征值来表示,即:

(17)
当ω≠0时,通过求解公式(13)得到一些离散的点。在分歧点e=4.5 μm以下,平衡点都是单一稳定且无变化的,每个e值都对应一个唯一的平衡点。随着内间隙的增加,并超过分歧点e=4.5 μm时,有3个平衡点,并且这3个平衡点的位置分布基本都是沿着同一曲线向两端延伸,如图5所示。

图5 动平衡点稳定区域与不稳定区域的分布
图5揭示了平衡点的分布与内间隙和轴承转速(ω=800 r/min)的关系。
通过数值分析证实了内圈存在着两种实质上不同的振动类型,以分歧点e=4.5 μm为临界点。对于小的轴承内间隙e<4.5 μm,振动是周期性的。当轴承内间隙超过分歧点时,就会出现沿Y轴对称分布的振动类型,在此命名为“井架”振动类型。在低转速,运动还是周期性的并且在Y轴的一定范围内。一旦转速提高,轴将会出现跳动情况,从“井架”的一端跳动到“井架”的另一端,也就是给定一个单一频率的输入信号ω,而输出的则是轴运动的随机广谱频率。此外,在相位空间,轴轨迹随时间的变化而变化,中心点和鞍点也在随机的变化。并且,随着转速的不断提高,会发生混沌现象。
4 案例分析与求解
案例1 零间隙滚动轴承
在零间隙滚动轴承中,承载区域的角度为π,承载的滚动体数目为N/2。通过常数变易法来求解在水平方向和垂直方向两种不同情况的解。
水平方向(x方向),转速在基本频率附近,则内圈的运动Nω≈ω1;垂直方向(y方向),转速在基本频率附近,则内圈的运动Nω≈ω2。
图6所示是零间隙滚动轴承在水平方向和垂直方向上的频率响应结果,并对广义积分变换法的计算结果与数值模拟仿真的结果进行对比分析。

图6 零间隙滚动轴承在水平方向和垂直方向上的频率响应结果
在两种情况下,广义积分变换法的计算结果与仿真结果具有较好的一致性。对于图6中存在的一点偏差,通过分析后主要有两个原因:1) 是对模型进行了假设,即假设是由Nω≈ω1或Nω≈ω2引起的主共振;2) 在对公式(7)进行近似求解时,忽略了振动模型在水平方向上和垂直方向上的耦合作用。
案例2 正的小径向间隙(0 在第2种案例中,为了进行广义积分变换法,对公式进行近似处理得到 (18) 在特定的周期0~2π内,依据i不同的取值情况,得到有效的近似结果。在数值模拟分析的过程中,为了匹配原始函数的值,我们将范围外的近似值设定为0。 对运动控制方程进行归一化处理,得到: (19) 通过常数变易法来求解公式(19)在以下两种不同情况的解。第一种情况,水平方向(x方向),转速在基本频率附近,则内圈的运动Nω≈ω1;第二种情况,垂直方向(y方向),转速在基本频率附近,则内圈的运动Nω≈ω2。 图7所示是正的小径向间隙滚动轴承在水平方向和垂直方向上的频率响应结果,并对广义积分变换法的计算结果与数值模拟仿真的结果进行了对比分析。 通过比较图6和图7可知,随着轴承间隙的增大会导致x方向和y方向上振动幅值的增大。此外,频率响应图说明了随着轴承间隙的变大,会使x方向和y方向上的共振频率降低。对于这种软化效应,主要是因为承载区域内滚动体数目在减少,并随着轴承间隙的不断增大,导致内圈单一的周期运动,这样就降低了振荡器的有效刚度。而且,这种在垂直方向上的影响效果要比水平方向上更加明显。事实上,轴承固有频率的阶数在间隙e=0到e=4.5 μm之间发生了反转。当e=0时,ω1<ω2,而当e=4.5 μm时,ω1>ω2。 图7 正的小径向间隙滚动轴承在水平方向和垂直方向上的频率响应结果 研究证实了轴承间隙与轴承振动有着密切的联系,为了验证理论模型的正确性和可靠性,结合改进的数值分析方法和台架试验对前序的2-DOF非线性模型和理论推导进行验证。 测试轴承的具体参数如表2所示,滚动体的内阻尼主要由润滑剂产生[11-13],轴承阻尼的理论计算是很难实现的,因为它要综合考虑到润滑剂的材料,黏度等因素。因此,将通过冲击实验来测定阻尼参数。 表2 测试轴承的具体参数 为了测定稳定有效的黏度,每一次测试都是在轴承运行20 min后进行测试,跑合装置如图8所示。 图8 跑合实验台 由于润滑剂的黏度对阻尼因素的影响比较大,因此在求解运动控制方程中,分两组对比实验进行说明,一组是标准的润滑油(v=15 mm2/s),参数见表2中轴承A;另一组则是高黏度润滑脂(v=110 mm2/s),参数见表2中∅127轴承。 滚动轴承在阻尼比为4.15% (通过冲击实验来测定阻尼参数)时测得的第1阶固有频率是2 941 Hz。因此,测试轴承的当量刚度可表示为 k=2.623 2×104(lc-2rc)0.92 (20) 式中:k为测试轴承的当量刚度,N/mm1.08;lc为滚珠接触之间的长度;rc为滚道边缘的半径。 在图9所示的试验装置中,采用3035AG加速度计来测量轴承的振动信号,其精度为100 mV/g。采用动态信号分析仪,并配备低通抗混滤波器来获取实验数据。数据采集及处理部分:通过传感器采集到的模拟信号经过隔离和放大,经A/D转换后通过端子板进入数据采集控制板,通过并行总线与计算机相连,在自主研发的程序控制下进行实验过程监测和数据的采集。 图9 实验台架 从相平面或者庞加莱映射中,可以直观的观察到系统的混沌特性。通过MATLAB整合与编程处理通过梯形方法得到的加速度数据,得到轴承振动的速度与位移分布图。为了更好的观察到奇异吸引子的存在,在实验中我们通过获取长的数据序列来增加庞加莱点的数目。在这次实验中,设定转速为600 r/min,采样频率为6 000 Hz,采样时间为30 min。然后对数据进行再采样,此时的采样频率为250 Hz,最后绘制庞加莱映射。图10所示为从整合与编译得到的加速度数据中提取的轴承振动的位移-速度分布。 图10 轴承振动的位移分布和速度分布 然而,如果一个系统没有足够的阻尼,那么混沌吸引子就会以不规则的云点形式存在,这种情况如图11a)所示。图10和图11a)的数据都是通过对标准油(v=15 mm2/s)润滑的轴承进行测试得到的数据。为了增加轴承的阻尼,对轴承圈和滚动体进行润滑脂(v=110 mm2/s)润滑,这样就使得阻尼从572.4 Ns/m增加到694 Ns/m。在图11b)庞加莱映射中,通过分形自相似特征的吸引子的存在证实了系统混沌行为的存在。在相同的阻尼参数、轴承尺寸参数以及相同的转速下,由实验数据得到的奇异吸引子的图(图11b))与通过求解运动公式(7)的结果接近。这种定性的结果不仅证实了轴承混沌行为的存在,而且验证了数学模型和理论推导的可靠性。 图11 台架实验结果的庞加莱映射 1) 结合振动信号与轴承振动的动力学特性建立了2-DOF非线性轴承模型,采用广义积分变换法分别求解轴承在零间隙和正的小径向间隙(0 2) 基于赫兹弹性接触理论分析滚动轴承动力学特性,得到轴承内圈的平衡点的个数取决于轴承的内间隙。当轴承间隙e<4.5 μm时,有一个稳定的平衡点,而且在平衡点中心附近,轴承内圈存在着周期振动。当轴承的间隙e>4.5 μm时,有3个平衡点。随着轴承内间隙的增加,会导致谐振频率的降低。 3) 当轴承间隙e>4.5 μm时,随着转速的变化,系统会产生混沌振动。随着轴承内间隙和转速的不断增大和提高,发生混沌振动的区域也不断增多。 4) 通过对两种不同轴承间隙的案例求解和实验结果证实了轴承振动模型的正确性与可靠性,进而为滚动轴承系统的振动控制提供了理论依据。

5 台架试验验证
5.1 轴承冲击实验


5.2 台架说明

5.3 试验结果分析


6 结论
