2UPS/RR脚踝康复机构设计与工作空间优化
2023-02-16吴广进卢宗兴于潇雁
吴广进, 卢宗兴, 于潇雁
(福州大学 机械工程及自动化学院,福州 350116)
并联机构具有刚度大,精度高,整体受力较为均匀,承载能力强,结构对称性好等特点,以上优点决定并联机构常运用于精度较高承载工况较大的环境中[1],但由于并联机构相对较为复杂,杆件受到运动约束,导致其工作空间存在不同程度受限[2],其控制较为复杂而少自由度并联机构能够一定程度上避免运动控制复杂性,目前,并联机构主要用于并联机床的研制,工业微动机器人,飞行模拟器,航天交会对接,医疗一起等现代尖端技术领域。
踝关节作为人体承重关节,在日常活动中参与奔跑、跳跃等活动,常受到不同程度的冲击[3],踝关节扭伤占全身关节扭伤占比居高,而踝关节外侧扭伤占踝关节扭伤占比近85%[4],在脚踝康复机构领域,李剑锋等[5]对机构驱动参数范围进行设定,求解出机构工作空间,通过雅克比矩阵分析脚踝康复机构运动学性能,求得机构灵巧性指标;刘芳芳等[6]通过螺旋理论进一步对该机构自由度进行分析,通过逆解方程求得机构一阶影响系数,采用搜索法求解机构可达姿态空间,表明机构具有良好的动态特性,但此机构运动控制稍复杂;樊晓琴等[7]基于踝关节运动特性及中医牵引康复疗法,研发出(2-SPS+PU)&R 混联式踝关节康复机构,结合闭环矢量法求得机构逆解,通过工作空间表明机构能够满足受损踝关节的康复需求;崔马茹等[8]提出 3-URPR 少自由度并联机构,应用螺旋理论计算机构自由度,应用闭环矢量法分析机构逆解,最后在逆解及确定结构参数下求得机构可达工作空间;上述研究虽都求得机构工作空间且均符合所要求的康复空间,但作者并未对机构参数布局对机构各性能影响进一步研究;严骋等[9]对新型三自由度纯转动并联机构进行结构设计,对影响机构工作空间的参数进行分析,求得机构工作空间与参数之间的关系,但并未进行进一步分析面积变化的原因。由于脚踝康复运动的独特性,且少自由度并联机构能够运用于脚踝康复。
在实际康复运动中,仅趾背屈及内外翻就能够覆盖大部分踝关节区域肌肉锻炼,且对后续康复训练能够起到一定的作用[10],内外旋运动在实际康复过程中出现程度较低。本文提出2UPS/RR少自由度并联机构,能够为踝关节提供趾背屈、内外翻及复合康复运动,其运动能够为踝关节肌肉提供康复训练,并且稳固的支撑结构能够使动平台承受一定重量的载荷时不发生摇动,本文通过对机构布局优化,使得机构工作空间满足踝关节康复需求。
1 2UPS/RR机构构型描述
近年来,并联机构与医疗康复交叉学科的研究较为活跃,本文结合并联机构上述优点及人体脚踝康复运动特性,开发研制2UPS/RR机构并将其应用于脚踝康复领域,2UPS/RR的并联踝关节康复机构如图 1所示。

图1 机构模型
机构主要由静平台、动平台,两条驱动支链及一条约束支链组成:每条支链中U代表虎克副、P为电机推杆,S为球副,其机构简单紧凑,运动副都为面接触,机构承载能力强。
1.1 坐标轴建立
2UPS/RR机构简图如图 2所示,定义坐标如:机构绕两旋转轴所在空间上的交点为点O,定义定坐标系O-XYZ原点位于点O,定坐标系的X轴方向水平朝右,Z轴竖直向上,根据右手螺旋定则确定定坐标系的Y轴;定义动坐标系T-UVW原点与动坐标系原点重合,初始位置状态下,两坐标系所对应的轴线重合,建立过程不再进行赘述。定义符号如下:定义约束支链中支撑杆两旋转副分别为R1、R2,Z轴与静平台交点设为O″点,Z轴与动平台交点设为O′点,两虎克副的旋转轴中心点分别设为ai点(i=1、2),两球副的球心点分别设为bi(i=1、2)。

图2 机构简图
1.2 自由度计算
黄真等[11]提出反螺旋理论分析机构自由度,使用机构反螺旋表示机构末端受到得约束;本机构由静平台、动平台、运动支链aibi(i=1,2)以及约束支链组成,运动支链采用UPS运动副,其中U副代表虎克副,P副代表电机推杆,S代表球副,两条支链左右对称分布,定平台通过虎克(U)副与推杆连接,动平台动通过球($)副与推杆连接,对机构运动支链aibi进行运动分析,且坐标的选择并不影响支链螺旋系,重新建立螺旋系分析,坐标如图 3所示,在机构初始布局下Ob1=(-43.65,6.02,394.05),Ob1为b1点在固定坐标系下的位置,其支链的螺旋系如下:

图3 UPS支链约束螺旋

图 4 闭环矢量图
(1)
求得式(1)中6个螺旋是线性无关的,对支链运用螺旋的互易积为零的原理来求解此运动螺旋系的反螺旋,即
(2)
可知此运动支链UPS对动平台未产生新的运动约束[12],同理另侧支链也未对动平台产生运动约束,则根据后侧支撑支链(RR)可知动平台能够绕X、Y轴旋转,同时根据 K-G(Kutzbach-Grübler)自由度计算公式[13], 机构的自由度可表示为

(3)
在空间自由度计算中,由于该机构不存在公共约束,选择机构阶数m=6,机构构件数(包括机架)n=5,机构铰链数g=6:分别为2个球副、2个虎克副、2个转动副;fi为第i个铰链所拥有的自由度;综上计算得到: 2UPS/RR机构具有2个自由度,所以该机构能够实现是通过两个电机推杆的直线运动输出转化为平台绕两个空间固定轴的旋转,进而带动脚底进行趾背屈及内外翻康复运动。
F=6×(5-6-1)+(3×2+2×2+2×2)=2
1.3 机构逆解
若要输出指定动平台位姿,则应当建立机构逆解模型[14];由动平台位姿α、β,通过逆解模型求得两推杆杆长变化规律,求机构逆解的关键在于建立机构输入输出之间的映射模型,本节通过闭环矢量法求解机构逆解。
机构动平台的位姿可通过先绕定坐标系中X轴旋转α角,再绕动坐标系V轴旋转β角,最终得到动坐标轴的位姿矩阵为:

(4)
式中:R(α,X),R(β,V) 分别为旋转矩阵; s=sin,
c=cos。
初始状态下推杆基座虎克副几何中心在固定坐标下的几何矢量Oai=(Xai,Yai,Zai)T,其中Zai=-h。初始状态下球副几何中心在动坐标系下的位置矢量Tbi=(Xbi,Ybi,Zbi)T;球副几何中心在定坐标系下的位置矢量为Obi;则可得
Obi=ORTTbi+orgPT=[Xbicβ+Zbisβ,Xbisαsβ+
Ybicα-Zbisαcβ,-Xbicαsβ+Ybisα+Zbicαcβ]T(5)
式中orgPT为动坐标系原点在定坐标系下的位置。
根据闭环矢量法求解踝关节康复机构的位置逆解,如图4所示。机构参数如表1所示。

表1 机构参数
Oai+Li=Obi计算机构逆解为
Li=Obi-Oai=[Xbicβ+Zbisβ-Xai,Xbisαsβ+Ybicα-
Zbisαcβ-Yai,-Xbicαsβ+Ybisα+Zbicαcβ-Zai]T
(6)
将表1中机构参数代入式(6)中得:
L1=[161.35cβ+9.05sβ-205,161.35sαsβ+
158.98cα-9.05sαcβ-165,-161.35cαsβ+
158.98sα+9.05cαcβ+385]T
(7)
L2=[-161.35cβ+9.05sβ+205,-161.35sαsβ+
158.98cα-9.05sαcβ-165,161.35cαsβ+
158.98sα+9.05cαcβ+385]T
(8)
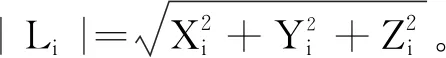
根据建立逆解的数学模型,已知动平台末端位姿参数(α,β)根据式(7)和式(8)两个独立方程,即可求得的两支链推杆长度|Li|(i=1,2)具体数值。
2 机构结构参数对工作空间影响
并联机构工作空间的大小和形状决定着机构的可达工作空间的大小,是衡量机构工作能力的一个重要指标[15-16],其主要受到以下因素影响:驱动副的行程;球副最大转角;推杆与动平台之间的干涉;连杆杆件间的干涉。
根据上述所得到的逆解公式(6),选取机构约束表达式为:
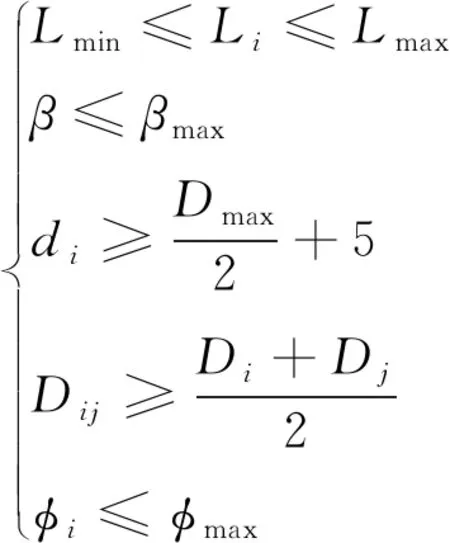
(9)

利用上述参数,结合点集法[18],规律性改变动平台位姿,绘制出机构工作空间,并使用包络线表示其边界形状,根据包络线区域内部点集数量,工作空间面积可以表示为
Area=Length(Piont)×Δα×Δβ
(10)
式中:Length(Piont)为包络线区域内部点的数量;Δα、Δβ为动平台变化的固定增量。
求得此时机构工作空间面积为1 107°2,由图5所示,初始布局机构背屈能够达到22°,趾屈能达到18°,内外翻接近为18°,结合表2人体踝关节康复所需运动角度,为使得机构工作空间满足脚踝康复空间,研究机构合理布局,使其能够满足脚踝康复的运动角度,以下研究机构布局对于工作空间的影响[17]。

图5 初始结构下的工作空间

表2 踝关节康复所需角度
2.1 球副最大转角对工作空间影响
球副的最大转角决定了球副连接两侧杆件的摆动范围,其转角大小影响机构的工作空间,讨论球副最大转角对工作空间的影响如图6所示,其工作空间面积如图7所示。

图6 球副最大转角对工作空间的影响

图7 球副角度对工作空间面积影响
由图6可知,当球副转角从20°增至30°时,机构趾背屈及内外翻空间 随着球副最大转角的增加而增大,当球副最工作角度由30°往上增加时,由于并联机构杆件与动平台存在干涉限制及推杆行程限制,此时工作空间的增加效果并不明显;由7可知,球副最大转角增加时,机构工作空间面积也随之增加;结合人体脚踝实际转动范围及机构受力等综合因素考虑,选取球副最大转角为30°。
2.2 球副安装间距对工作空间的影响
研究球副安装间距对工作空间的影响,通过调整两球副距VOW平面距离,即b1、b2的U坐标绝对值大小(表1),研究其对工作空间的影响。
在初始布局条件下,对机构球副安装间距进行内移分析(即减小bi点U坐标绝对值),如图8所示,当球副安装位置从初始位置向内移至30 mm的过程中,由于内移使连接杆开度减小,在推杆行程不变情况下,机构内外翻角度呈增大趋势,当两连接杆开度内移30~50 mm之间时,这是由于动平台与推杆间运动干涉限制,导致内外翻的角度呈减小趋势;如图9所示,球副在内移0~30 mm过程中,工作空间面积由1 519°2增加至1 683.8°2,球副在内移30~50 mm过程中,工作空间面积由1 683.8°2减小至1 583.3°2。综上考虑机构使用性及紧凑性,将机构球副内移30 mm。
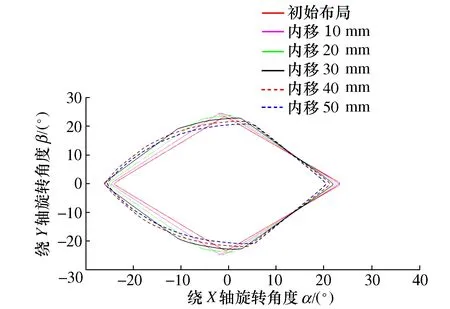
图8 球副内移距离对工作空间影响
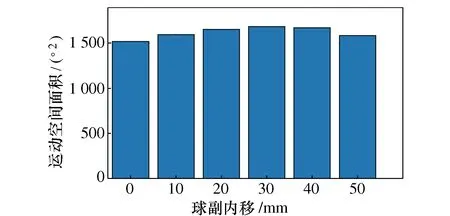
图9 球副内移距离对工作空间面积影响
2.3 推杆基座间距对工作空间的影响
研究两推杆基座安装距YOZ平面距离对工作空间的影响,通过调整两推杆基座距YOZ平面距离,即a1、a2的X坐标绝对值大小(表1),研究其对工作空间的影响。
在初始布局条件下,对机构推杆基座进行内移分析(即减小ai点X坐标绝对值大小),如图10所示,由最初机构初始布局下,基座均向内移动0~30 mm区间内,机构整体运动角度并未有较大幅度的增加;当基座向内移30~50 mm区间内,机构内外翻角度呈减小趋势,是由于动平台与推杆间存在运动干涉限制,导致内外翻幅度减小;如图11所示,推杆基座内移0~10 mm过程中,机构工作空间面积呈增大趋势,推杆基座内移10~50 mm过程中,机构工作空间面积不断减小,这是由于推杆和动平台干涉存在的结果;综上考虑机构使用性及紧凑性,将机构基座间距内移30 mm。

图10 推杆基座内移对工作空间面积影响

图11 推杆基座内移对工作空间面积影响
2.4 推杆前后位置对工作空间影响
研究机构推杆前后安装位置对机构工作空间的影响,通过同时调整球副安装座及推杆基座前后位置,即同时改变ai的Y坐标及、bi点V坐标(表1),研究推杆安装位置与工作空间之间的关系。
如图12所示,当推杆整体向后移动时(Y轴负方向),机构内外翻空间并未有增加,这是由于并联机构动平台与推杆干涉限制使其内外翻空间并未有过多增加,机构趾背屈工作空间呈增大趋势,这是由于在推杆行程一定的情况下,推杆越靠近旋转中心,机构趾背屈范围呈增大趋势;如图13所示,机构面积随着推杆位置后移而增大,但杆件后移过程中,不仅需考虑推杆空间位置与后部支撑杆干涉,还需兼顾机构输入速度与输出速度之间的比例关系(即机构雅克比矩阵)不宜过于大[18];综上所述,将推杆整体后移30 mm,作为最终推杆安装位置。
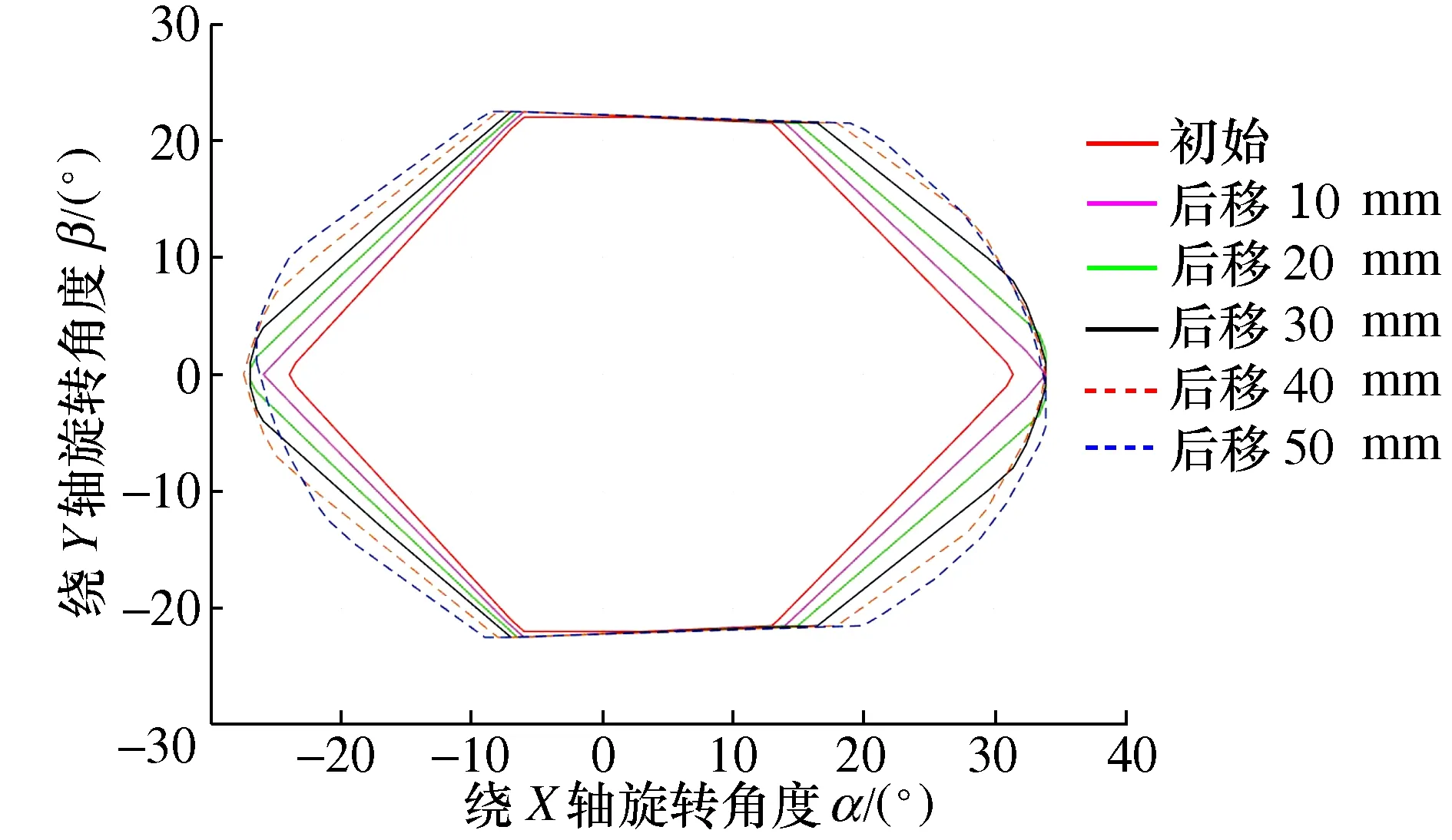
图12 推杆前后位置对工作空间影响
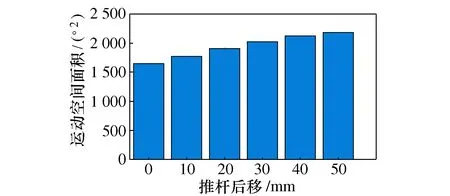
图13 推杆前后位置对工作空间面积影响
机构结构布局确定情况下,最终工作空间如图14所示。
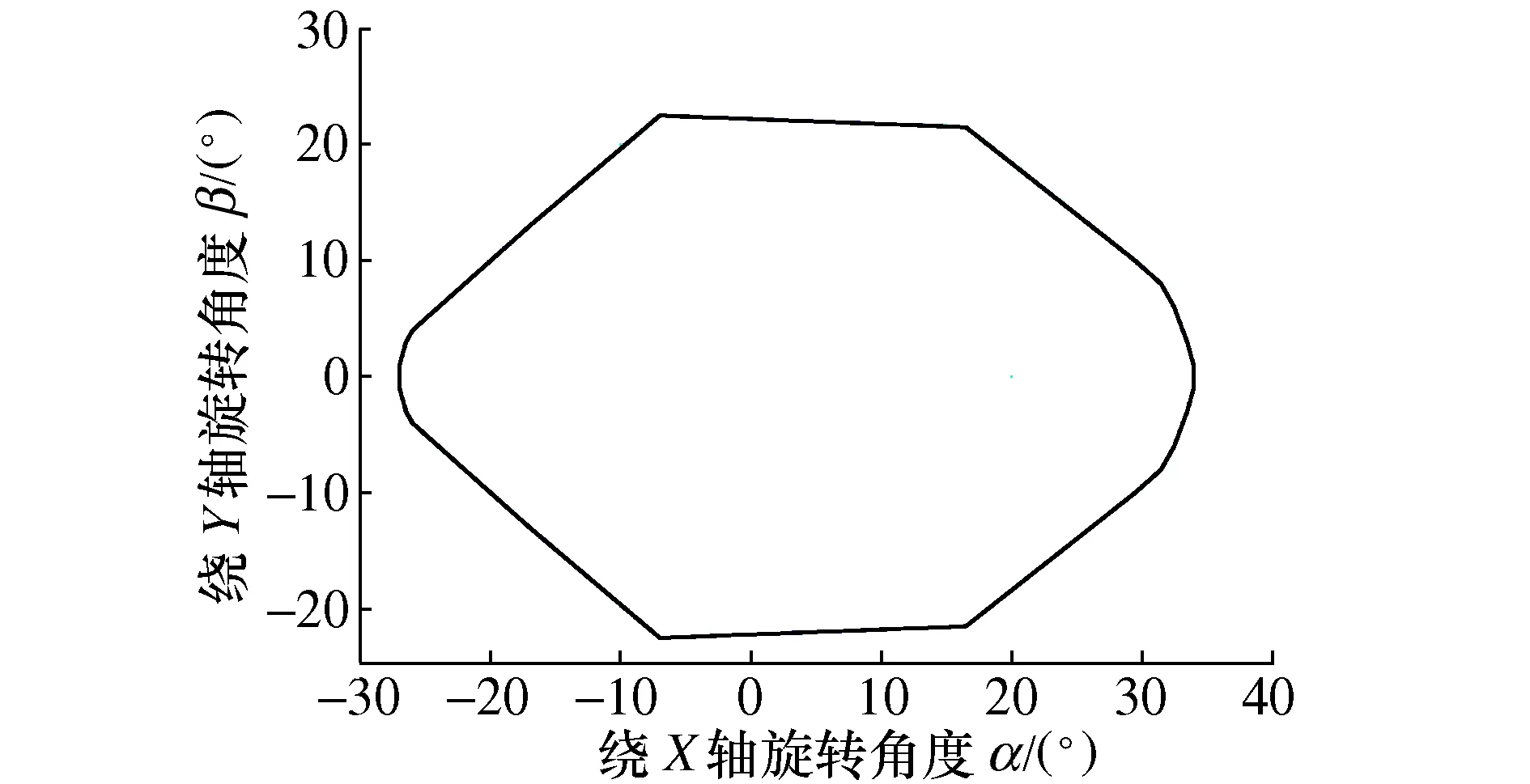
图14 最终工作空间
机构最大背屈达到34°,最大趾屈达到-28°,机构内外翻能够到达22°,机构工作空间面积2 025.75°2,结合表2所示,最终机构布局下的工作空间满足脚踝康复要求。
本节主要研究机构零件布局对机构工作空间的影响,目的在于找出两者之间映射关系,并研究分析工作空间变化原因,为机构布局及工作空间关系提供研究基础及理论依据。
3 机构算例分析
3.1 机构工作空间
根据上述机构转动空间的分析,得出符合踝关节康复的机构布局,通过上述确定下的机构布局,可以求得动平台中心点(O′点)的运动空间,如图15所示,从图中可以看出,O′点运动空间与脚底板下方的工作空间类似:呈凸出曲面;中心点运动空间过渡平滑且内部无空缺,表明在此空间内运动光滑连续且不存在奇异位型。
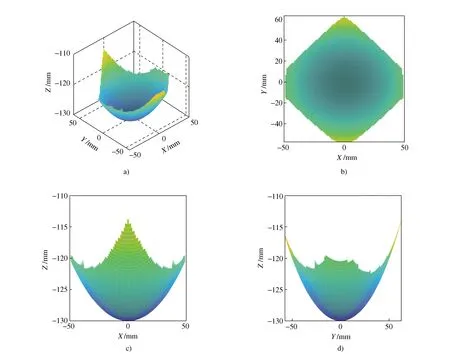
图15 机构O′点工作空间
3.2 MATLAB算例
将公式(8)和公式(9)逆解方程导入MATLAB中进行编程,设置动平台运动规律α=-20cos(πt/10)、β=20sin(πt/10),得到两杆杆长随时间的变化曲线如图16所示。

图16 MATLAB杆长逆解
3.3 ADAMS运动算例验证
2UPS/RR脚踝康复机构模型简化,去除不必要的特征,并导入ADAMS中设置相应约束及运动副,模型简化及约束结果如图17所示。在此模型正确约束下,得到机构自由度为2,验证上述求得机构自由度;进而在旋转副中添加旋转驱动,设置趾背屈运动副类型revolute、函数(时间)-20cos(πt/10)、设置内外翻运动副类型revolute、函数(时间)20sin(πt/10);上述设置后使得使动平台在空间上作章动复合运动[19],通过仿真测量机构两杆杆长变化如图18所示。
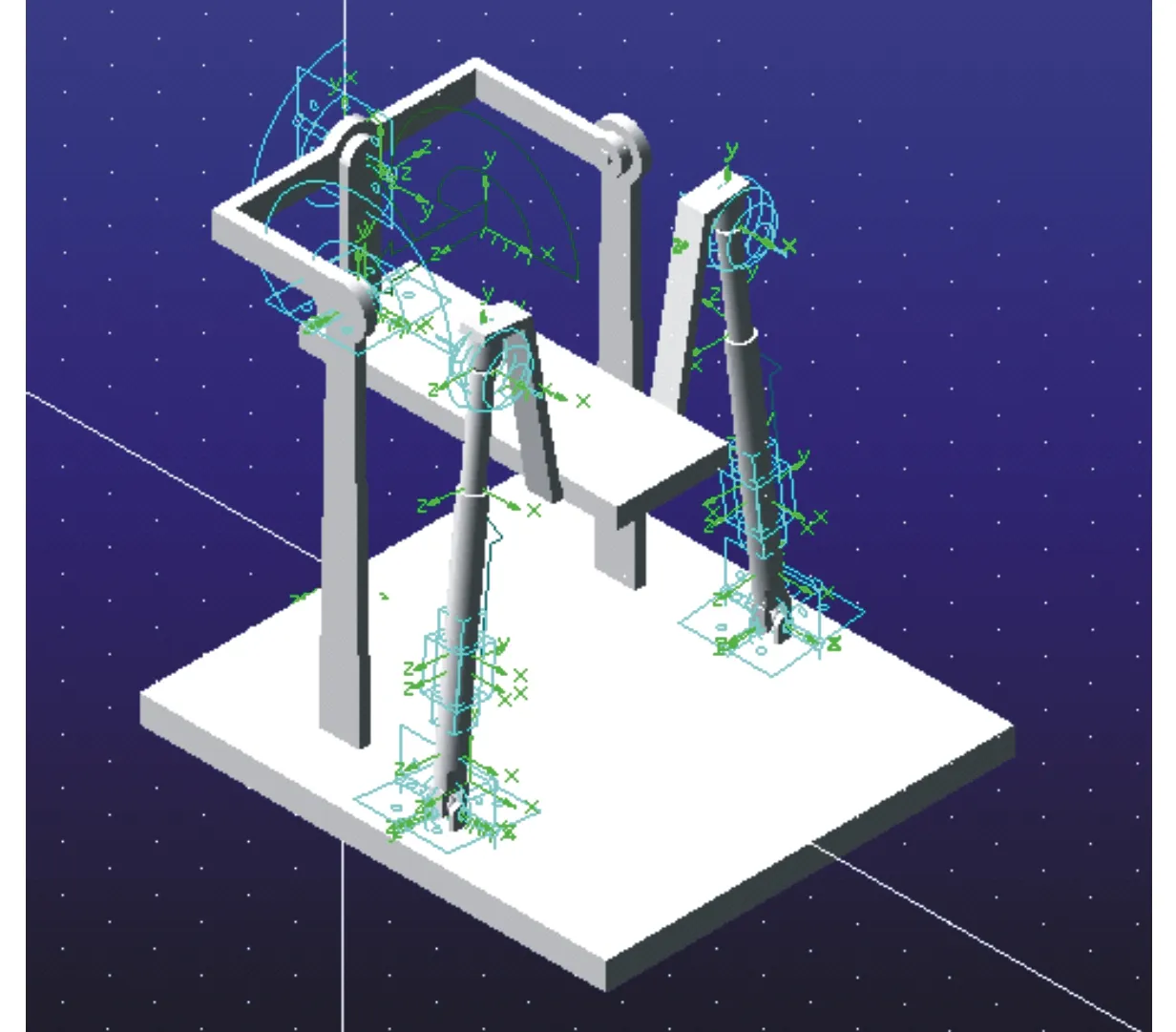
图17 ADAMS模型
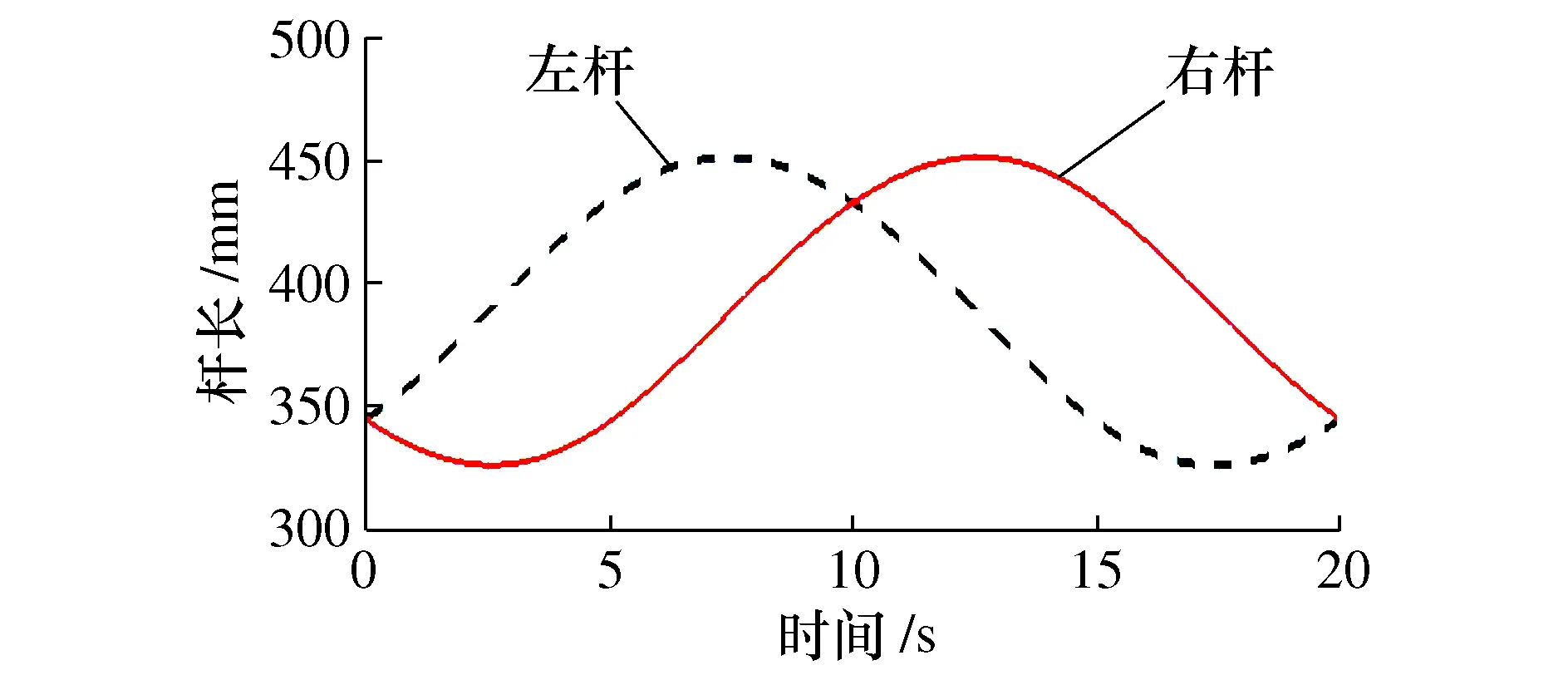
图18 ADAMS算例仿真
将MATLAB杆长数据(图16)及ADAMS仿真杆长数据(图18)进行对比,其杆长变化对比如图19所示,可得机构逆解方程正确性,两图中数据稍有偏差但趋势一致,主要来自于ADAMS模型测量点选取的误差,这一偏差并不影响运动算例验证;从上述实例表明不仅在理论计算上,而且在仿真模型中,均能实现机构动平台绕Z轴做20°的章动运动。

图19 ADAMS与MATLAB 比较图
计算动平台中心点(O′点)的三维轨迹,倘若机构轨迹点中断或不连续,则机构因杆件干涉等原因无法完成指定运动轨迹。由图20可以看出,点轨迹并不连续,这是因为该处因杆件干涉等原因,O′点无法到达而形成中断的轨迹;而当机构做20°章动复合运动时,O′点在已半径为130sin(π/9)做圆周运动,运动轨迹如图21所示,参考点在空间中运动连续平滑且无中断,表明机构做20°章动过程中并未有杆件间干涉。

图20 杆件干涉时O′点轨迹
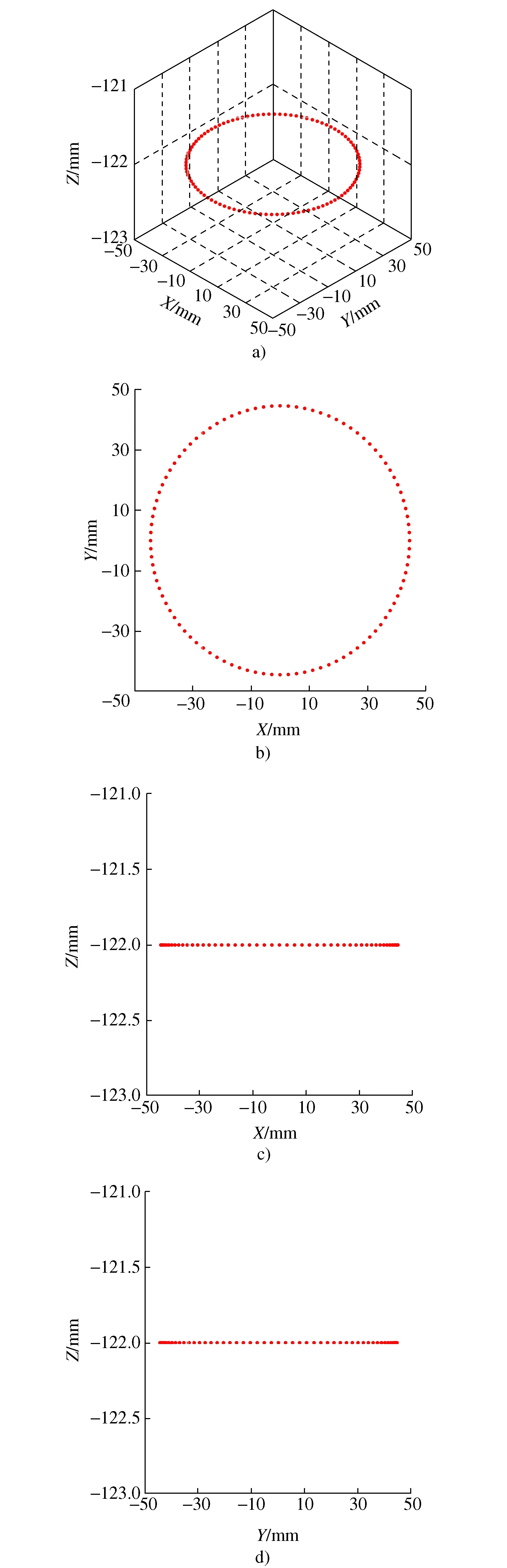
图21 O′空间运动轨迹
4 总结和展望
1) 求解机构运动空间过程中,不仅考虑干涉问题,而且以实际运动情况上引入安全间距5 mm概念,保证求解出工作空间满足安全要求又符合实际。
2) 优化前机构运动角度不能够覆盖脚踝康复空间;优化后内外翻角度增加10°,趾背屈角度增加20°,优化后机构运动角度能够覆盖脚踝康复空间。
3) 优化前的机构工作空间为1 107°2,优化后的机构工作空间为2 025.75°2;最终机构工作空间大幅度提升,通过与踝关节康复角度对比,其能够覆盖脚踝康复空间,所设计机构符合脚踝康要求。
4) 通过模型仿真分析验证机构运动连续性及机构逆解正确性,对以运动空间为目标参数的机构优化提供了优化方向及理论基础;后续可引入雅克比矩阵、机构灵巧度对机构运动平顺性进一步分析。
