滚动轴承剩余使用寿命预测综述
2023-02-16张金豹邹天刚王敏桂鹏戈红霞王成
张金豹, 邹天刚, 王敏, 桂鹏, 戈红霞, 王成
(中国北方车辆研究所 车辆传动重点实验室,北京 100072)
现代工业发展过程中,大型高端的关键机电设备呈现出复杂化、自动化及集中化的发展趋势,并且往往处于高负荷、变工况的连续运行状态。为确保机械设备的正常工作以及便利维修,必须加强对机械设备初期的可靠性设计,以及投入使用后的在线监测和健康管理。由于机械设备结构复杂,导致子部件之间产生较强的耦合干涉,兼之运行过程中内外非线性因素如阻尼、变刚度和时变外载荷等的影响,使得精确的物理模型难以建立并应用于监控和预测。在大数据的时代背景下,美国的工业互联网,德国的工业4.0等都在促使基于数据驱动的健康评估框架搭建形成以及信息管理系统的开发,因此PHM应运而生[1]。PHM分为故障预测和健康管理与维修两部分。在故障预测部分,PHM首先借助传感器采集关键零部件的运行状态数据,如振动信号、温度图像、电流电压信号、声音信号及油液分析等,提取设备的运行监测指标,进而实现对设备关键零部件运行状态的早期识别[2-3]。PHM通过建立完备的待监测零部件故障特征数据库,采用特征变换如主成分分析(PCA)和非线性流形算法,或者特征选择进行维数约简,结合机器学习算法如人工神经网络(ANN),支持向量机(SVM)等对其运行状态进行诊断和RUL预测,最终实现决策管理[4]。现在国外已建立的PHM研究机构有美国辛辛那提大学的(IMS)中心、美国马里兰大学的先进生命周期工程中心、法国的FEMTO-ST研究所等。
PHM使得维修活动从以往被动的事后维修、定期维修、视情维修等阶段,过渡到主动的预测维修[5-7]。预测维修的核心在于RUL预测,进而能够更有针对性地安排生产任务和制定合理的维修计划,实现生产效率的最大化,并且避免恶性突发事故的发生。因此国家中长期科技发展规划纲要(2006~2020)与机械工程学科发展战略报告(2011~2020)均将“重大产品和重大设施的寿命预测技术”列为重要研究方向。滚动轴承作为旋转机械的关键零部件,广泛应用于航空航天装备[8]、交通运输工具[9]及风力发电设备[10]等领域。这就要求滚动轴承适应各种复杂恶劣的工作环境,在高负荷和变工况的情况下能够保证高精度的连续运行,并且承受住各类冲击,因此往往成为机械系统出现故障的根源。统计表明,在高速动车组传动系统中,轴承故障类型主要集中在轴箱轴承和齿轮箱轴承,分别占故障轴承的48%和46%。轴箱轴承故障主要集中在外圈,占比高达63.6%;齿轮箱轴承中发生故障的零件占比基本相近;电机轴承故障则主要发生在内圈和外圈[9]。在风力发电齿轮箱设备中,轴承的故障比例高达76%[10]。根据ABB公司、电气和电子工程师协会和电力研究院的统计数据[11],感应电机中轴承的损坏比例最大,分别为51%,41%和42%。因此在滚动轴承投入使用初期,应当对其进行可靠性评估,防止突发性失效的发生,保证批次产品在其使用过程中的可靠性要求。在此基础上,对滚动轴承进行进一步的运行状态健康评估才有意义。但传统基于大样本寿命数据的滚动轴承健康评估主要基于概率统计分布如威布尔分布[12],得到的预测结果表征的往往是总体特征,如平均故障间隔时间等,其失效率曲线整体一般呈现出浴盆形式。因此制定的维修间隔相对固定,主要用于计划维修。其结果就是,如果过早维修会产生浪费,不及时维修又会造成安全隐患[13],所以该方法无法体现个体差异。
为实现滚动轴承的预测性维修,则需要对其失效过程数据进行研究[14]。滚动轴承的失效模式包括磨损、接触疲劳、摩擦热过大引起的热失稳或固体润滑的热退化而导致的胶合、保持架断裂、塑性压痕和锈蚀等[8],如图1所示。

图1 实验轴承损伤
其中磨损是其主要失效形式,一般发生在滚道与滚动体之间,原因可能有异物进入、载荷冲击、安装不当、设计与制造、润滑不良等[9]。磨损会使轴承的游隙、表面粗糙度增大、旋转精度降低,同时也会加剧轴承磨损,在振动方面主要表现为振动幅度增大,所以基于振动信号的诊断技术得到了广泛应用。与温度图像、电流电压信号、声音信号及油液分析等信号相比,振动信号对轴承的状态变化响应速度快,包含了轴承运行状态变化的大多数有用信息,能很好的反应出轴承故障的类型和位置,并且容易提取,便于自动化和在线诊断,是一种无损检测技术[15]。与寿命数据相比,退化特征数据可以节省试验时间与费用,能够体现外部环境以及内部多种因素对产品性能的动态影响,使得相关的评估和预测结果更具有指导意义。
为适应实际工程的应用,滚动轴承的理论研究需要考虑更多更复杂的使用条件,譬如在复杂恶劣的工作环境下,如图2所示[16],滚动轴承振动信号在传递途径中受到背景噪声和其他耦合部件的干扰,极易造成微弱故障信号的淹没,导致测得的振动信号具有非平稳性、非线性、非高斯性和低信噪比的特点[17]。为准确地对复杂工况下的滚动轴承进行健康评估,需要多个传感器在不同位置对数据进行全面采集,并且是高频采样,以确保有效信息不被遗漏,但这也进一步导致了海量数据需要处理[18]。因此在滚动轴承运行状态评估中,首要问题就是如何从振动信号中提取有效的故障特征,并且实现有效特征地融合。

图2 从系统到数据采集
在此基础上,基于对故障失效机理的认识程度和掌握数据的多少,来选择不同的模型进行故障诊断和RUL预测[19]。预测模型的选择至关重要,如果选择不当会导致预测结果与实际情况存在巨大误差,甚至预测失败。尤其现阶段设备的使用工况更加复杂和多样化,导致同工况下滚动轴承的参考样本数量严重不足,这进一步增加了寿命预测建模的困难。但同时存在大量其它工况下的参考样本可以借鉴,从而借助人工智能进行RUL预测,这也促使了迁移学习在滚动轴承RUL预测中的应用。
针对上述滚动轴承RUL预测中出现的新的问题和发展方向,基于PHM框架对预测过程中出现的各个环节进行了梳理和讨论。首先在实验数据的基础上,对滚动轴承振动信号的产生机理、信号降噪、特征提取、降维和融合及得到的性能退化指标进行介绍与对比。然后结合数据驱动算法,对滚动轴承的RUL预测方法、模型选择和评估标准进行了阐述,并对其发展趋势进行了讨论和展望。
1 性能退化指标
1.1 试验数据及分析
PHM中RUL的预测涉及特征提取、运行状态监测、故障诊断等内容,其中运行状态监测用于判断运行状态是否正常,如果发生故障,需要对故障类型和损伤程度进行识别。然后再以当前装备的使用状态为起点,结合已知预测对象的结构特性、参数、环境条件及历史数据,对滚动轴承的RUL进行预测,从而定量的对滚动轴承的健康状态进行描述,形成最终决策。
上述各部分内容的研究均需要滚动轴承试验数据的支撑,需要对其运行信号特点进行分析,进而提取特征进行定量表征。收集的滚动轴承数据包括基于加速寿命试验的滚动轴承寿命数据[20-23]、CWRU人工故障轴承数据[24-25]、IMS轴承全寿命数据[26]、全寿命数据[27]、PHM2012轴承RUL预测竞赛数据[28]、变转速轴承测试数据[29]、复合故障轴承数据[30]以及作者在杭州轴承试验研究中心(HBRC)采集的滚动轴承全寿命数据,轴承的相应测试装置如图3所示。

图3 滚动轴承测试装置
在研究滚动轴承振动信号过程中,主要研究轴承因磨损损坏而产生的振动。损伤引起的振动有两种类型:一种是由轴承损伤点处受到反复撞击而产生的,其频率与轴承的性质有关;另一种是因损伤冲击而诱发的高频固有振动。因此,在试验的基础上进行滚动轴承动力学建模,是深入理解故障产生机理的重要手段[31-32],为滚动轴承PHM研究提供理论研究基础。Buzzoni等[33]开发了非平稳条件下滚动轴承故障信号的仿真平台,该平台可以模拟单一轴承故障,或者多级变速箱中的单点局部故障和分散轴承故障,还可以考虑输入轴的变速剖面,以及线性定常系统的循环平稳贡献和影响。
1.2 特征提取与融合
1.2.1 信号降噪
信号预处理方法包括平滑处理、剔除奇异值点、消除趋势项和降噪等[34],其中信号降噪对微弱特征的提取至关重要。对于滚动轴承故障信号,常用的降噪方法包括信号重构降噪、故障信号增强降噪和稀疏分解降噪。
1) 信号重构降噪方法最为常见的是小波降噪,主要有空域相关滤波和小波域阈值滤波两种,其中空域相关滤波通过考虑信号的小波系数在不同尺度间的相关性强弱进行筛选,小波域阈值滤波则是通过设定阈值进行去噪[26]。在此基础上发展起来的方法有小波包分解降噪、以经验模态分解[35]为代表的自适应模态分解降噪等。其它信号重构方法包括混沌序列相空间重构、奇异值分解降噪和形态滤波降噪等。
2) 故障信号增强方法的特点是通过数学方法放大故障信号中的冲击成分,进而突出故障信息,主要方法有Teager能量算子及其改进方法、稀疏编码收缩、最小熵解卷积方法、最大相关峭度解卷积算法和随机共振等。
3) 信号稀疏表达方法[36]如匹配追踪、基追踪等通过原子分解对振动信号进行近似表达,从而实现故障信号的稀疏分解。原子分解建立在冗余字典的基础上,包括傅里叶原子库、小波原子库、脉冲原子库以及线性调频原子库等。
1.2.2 特征提取
提取的故障特征分为时域统计特征、频域特征、非线性特征以及时频域图像特征等。时域统计特征和频域特征如表1和表2所示。

表1 时域统计特征

表2 频域特征
针对滚动轴承故障信号的随机性特点,在统计特征方面除表1中非参数统计量外,还可以提取概率分布的特征。例如陈昌等[37]对采集的全寿命振动信号逐个时间点进行希尔伯特变换,保证信号变换后的非负性,然后采用威布尔分布进行拟合,提取形状参数作为滚动轴承的性能退化指标。该方法简单易行,但在滚动轴承的全寿命过程中无法保证每个时间点的振动信号都符合威布尔分布。为避免分布假设,Cong等[38]基于非参数Kolmogorov-Smirnov(K-S)检验统计量直接对原始振动信号进行分析,实现了滚动轴承的运行状态监测,因此更具有通用性。另外,Wang等[39]梳理了近年来谱峭度在滚动轴承故障诊断与预测中的应用。
针对滚动轴承故障信号的非线性特点,用于表征故障的非线性特征包括数学形态学分形维数[40]、分形谱参数[41]、李雅普诺夫指数[42]、Lempel-Ziv复杂度等[43]以及熵等。其中,熵是一种表征振动信号复杂度的方法,具有明晰的物理意义。滚动轴承运行初期,采集信号主要是正常振动信号和背景噪声,呈现很强的随机性,因此对应的熵值就会很大;当滚动轴承存在故障时,采集到的信号具有周期性冲击特点;当故障较为严重时,冲击信号比干扰噪声更为明显,因此对应的熵值就会较低。迄今为止,表征滚动轴承状态信息的熵值基本量有近似熵[44]、样本熵[45]、模糊熵[46]、排列熵[47]、散布熵[48]和维纳熵[49]等,以及在此基础上对基本量进行多尺度化[50-51]、精细化、广义化、复合化等[52]得到不同类型的改进熵。另外,基于信号分解得到的熵包括复小波包能量矩熵[53]、经验模态分解能量熵[54]、局部特征尺度分解相对谱熵[55]等。其它常用的熵值还包括功率谱熵、包络谱熵、奇异值熵、符号动力学熵等。
针对滚动轴承故障信号的非平稳特点,一种方法是通过自适应模态分解得到若干平稳得本征模态函数,然后再进行特征提取;另一种是采用时频分析进行处理,并在得到的时频图像上提取的特征。提取的图像特征大致可归纳为:颜色或灰度的统计特征;纹理、边缘特征;形状特征[56]。章立军等[57]采用平滑伪威格纳-维尔分布表征轴承振动信号的时频能量分布特征,并利用灰度共生矩阵的统计特征作为轴承的性能退化特征。Wang等[58]采用滚动轴承振动信号的双谱图像特征进行性能退化表征。其它图像特征还有局部二值模式图像的纹理特征[59],对称点图案的形状特征参数[60]以及递归图熵[61]等。随着深度学习的发展,在滚动轴承的故障诊断和寿命预测中可以直接将图像信息作为训练样本,不需要再进行特征提取。
1.2.3 特征选择与降维
多域特征能够更全面地反映振动信号中蕴含的故障信息,但并不是所有特征都具有相同的表征效果,部分特征只针对某些故障类型具有敏感性,同时多个特征参数的相关性或耦合关系亦会造成诊断过程中计算代价过大和诊断结果的不准确性。所以滚动轴承进行故障监测、诊断和预测时需要对提取的特征进行针对性的选择和变换,通过降维来提取对各类工况敏感、可分性强的特征,防止维数噪声的引入,进而提高评估和预测模型的复杂度,降低计算代价,并进一步增加可视性。
故障诊断和性能退化的特征评价选取具有不同特点[62]:故障诊断需要特征之间大间隔,可分性更强;性能退化特征则需要对服役周期内的特征序列进行整体分析,侧重于一致性趋势分析。在滚动轴承故障诊断的特征提取中,多以自适应模态分解为主;在性能退化特征提取时则多采用小波包分解[63]。
滚动轴承特征选择方法主要分为:过滤式、封装式、嵌入式和集成式[64]。过滤式特征选择计算自变量和目标变量之间的关联性,如相关系数、互信息系数等,可解释性好,主要算法有Fisher分值、Laplacian分值(LS)、熵权法筛选、补偿距离评估技术[65]、Mahalanobis-Taguchi系统[66]和粗糙集[67]等。张彬[62]根据全寿命特征的单调性、趋势性和鲁棒性进行特征选择,各项指标表达式如下:
1) 单调性
单调性可以简单地利用差分进行计算

(1)
式中:K为特征的长度;No. of d/dx>0指特征中某点和其下一个特征点组成的向量单调上升的数量;No. of d/dx<0指特征中某点和其下一个特征点组成的向量单调下降的数量。
2) 趋势性
退化特征的趋势和时间应当具有相关性,若接近于1或-1说明其相关度越强。一般采用Pearson相关系数和Spearman相关系数描述两个序列的相关性,其计算方法分别为:

(2)

(3)
式中:X,T分别为两个时间序列;n为变量的个数;di为两个序列变量在顺序排序后更新后秩次的差。Pearson相关系数要求数据需尽量满足正态分布的假设且受到异常值的影响较大,因此适用性较窄。作为Pearson相关系数的改进方法,Spearman相关系数的适用性更强。
3) 鲁棒性
由于运行环境等的影响,特征往往会具有一定的噪声,噪声的存在会降低预测结果的稳定性。一个好的退化特征应具有一定的鲁棒性才能容易辨别出退化状态的各种阶段。特征鲁棒性的表达式为

(4)
式中:K为总观察次数;X(tk)=XT(tk)+XR(tk),XT(tk)为经过平滑处理后的平均趋势,XR(tk)为波动项。该指标在使用时应当选择适当的平滑处理方法,并且在做特征对比时,应当采用相同的平滑处理方法和参数。Javed等[63]、Wu等[68]、柏林等[69]均采用此方法用于滚动轴承敏感退化特征的选择。
封装式特征选择通过优化目标函数来决定是否加入或去除某个变量,迭代产生特征子集,如遗传算法[70]等。嵌入式特征选择采用正则化算法如套索算法,使得分类器能够自动选择特征。集成式特征选择具有良好的稳定性,但时间性能一般。4种方法在特征分辨、解释性、稳定性和时间性能等方面各有千秋,可根据实际情况加以选择。

图4 降维方法概况
由于PCA基于正态分布假设和线性变换,对异常数据比较敏感,因此非线性降维算法越来越受到关注和研究,主要包括动态PCA[68]、核主成分分析(KPCA)[74-75]、投影寻踪[76]、特征矩阵联合近似对角化[77]以及流形学习等。KPCA借助核函数技巧辅助PCA来实现非线性特征的提取,但是核函数及参数在选取时是需要预先给定的,选择不当会导致类可分性测度很小。投影寻踪通过构造投影指标函数实现降维,能够处理高维非正态、非线性问题,稳健性较好。特征矩阵联合近似对角化方法由 Cardoso 提出,该算法利用高阶累积量将独立成分分析问题转化为特征矩阵对角化问题进行求解。
近年来,流形学习算法因其良好的非线性维数约简性能,使其广泛应用于机械故障诊断中,主要算法[78-79]有等距映射(Isomap)、局部线性嵌入(LLE)、邻近保持映射(NPE)、局部切空间排列(LSTA)、拉普拉斯特征映射(LE)、局部保持投影[80-81](LPP)和正交局部保持投影[82-83](OLPP)等。上述算法的主要区别在于对每个数据周围信息的局部表达不同。流形学习算法分为有监督算法和无监督算法两类,其中监督算法用于故障分类[83],无监督算法用于运行状态监测[81]。流形学习虽然取得良好的效果,但依然存在非敏感特征干扰和邻域大小选择等问题,因此在降维前需要对特征进行初步筛选,去除冗余特征。
基于图像二维特征,Li等[84]采用2D-PCA对快速傅里叶变换得到的频谱进行降维分析;陈守海[85]采用二维LPP对希尔伯特时频谱进行降维;蔡蕾和朱永生[86]采用非负矩阵分解对时频图像进行压缩。二维降维方法为后续张量学习和深度学习提供了预处理。
1.2.4 特征融合
一般情况下,滚动轴承在其全寿命服役过程中,要经历从正常运行,到性能退化阶段,再至完全失效阶段等3个阶段。以IMS中心第二组#1轴承为例,其全寿命振动信号如图5所示,可以比较清晰地显示出3个阶段。El-Thalji等[87]进一步将其细分为5个阶段,分别为磨合期、稳定期、故障初始期、故障发展期和快速增长期,如图6所示。

图5 IMS中心#2-1测试轴承外圈故障全寿命周期振动信号
鉴于滚动轴承退化的复杂性,其退化阶段的划分应根据实际情况具体分析[88]。滚动轴承的退化演变过程虽然无法通过直接测量内外滚道和滚动体的磨损程度来进行表征,但却能通过外部表征如振动、噪声、温度变化等参数体现。因此可以从振动信号中提取多种特征进行融合,间接得到运行监测指标来描述滚动轴承当前状态与正常状态的偏离程度,以便尽早发现故障。然后通过各类模型建立监测指标与滚动轴承寿命的映射关系,从而实现监测和预测[89]。何正嘉等[90]总结出若干种归一化的运行监测指标,如相关系数法、峭度指标法等,建立了设备运行状态和可靠度之间的映射关系。但是单一的特征参数往往只对轴承特定运行阶段或特定故障类型有效,所以需要融合多种信息特征的方法以取得准确的监测结果。Wang等[2]将基于振动信号的健康指标分为:基于机械信号处理、基于模型和基于机器学习。滚动轴承健康监测指标可以分为非监督指标和监督指标,其中非监督指标包括基于边界法、基于概率统计和基于模型重构。
1) 非监督指标
此外,队员们在扶贫工作中也不忘自己的“老本行”,严厉打击各种违法犯罪,同时做好相关法律法规、禁毒防艾等的宣传工作。工作队驻村期间,曼来村实现了治安案件零发生,吸毒贩毒案件零发生。村庄的社会治安稳定了,人们也能安心地搞生产了。
基于边界法。该方法寻找一个尽可能包含所有健康数据的最优超球体,通过计算监测点与超球体圆心的距离来实现运行监测,主要算法有支持向量数据描述(SVDD)[58, 69, 91-92],马氏椭球学习机等。当SVDD为高斯核函数时,SVDD和单分类支持向量机具有等价性。马氏椭球学习机为SVDD的一种变型,使用马氏距离(MD)代替SVDD中的欧拉距离,实现了超椭球面来代替超球面。武千惠和黄必清[93]采用粒子群优化算法对SVDD的核函数参数进行估计;Zeng等[94]对SVDD的超球面进行了重构并提出凸包单分类算法;Shen等[95]引入模糊理论对SVDD边界进行改进,以上研究均成功地在滚动轴承运行监测中得到了应用。
基于概率统计。该方法通过度量滚动轴承健康数据与监测数据两者的概率分布距离实现运行状态评估,主要算法包括威布尔分布极大似然函数[37]、K-S检验[38]等。Soualhi等[16]提出了同时考虑信号时域和频域的健康指标。Wang等[96]通过振动信号的平方包络统计值,得到两个无量纲广义健康监测指标。对于多个统计特征的融合,Qiu等[70]采用遗传算法选择敏感的特征,通过加权实现了健康监测指标的构建。Rai和Upadhyay[97]基于MD计算运行状态特征偏离健康状态特征的程度,通过MD的累积和构建了滚动轴承的运行监测指标。Hong等[98]以正常特征空间为基准,通过高斯混合模型(GMM)来测量其与待测特征空间分布之间的偏离值,并将其作为置信值(CV)来描述轴承的性能退化过程。当轴承处于健康状态时,两个函数基本重叠,CV趋近于1;当发生故障时,CV接近于0,因此GMM可以利用CV从1到0来体现轴承的退化过程。Zhang等[99]采用连续马尔科夫模型的非负对数似然概率作为滚动轴承的监测指标。Ni等[100]基于随机矩阵理论,采用单环机器学习提取均谱半径、最大特征值和内圆随机点数据作为监测指标。
基于模型重构。该方法通过最小化重建误差,将原特征向量映射到子空间,在此映射过程中提取特定过程参数作为监测指标。其中最为常用的是基于PCA进行非监督特征降维得到的两种指标:平方预测误差(SPE)和Hotelling-T2[101]。类似的,Duan等[102]基于KPCA,Yu[81]基于LPP,分别得到T2统计量和SPE两个监测指标用于滚动轴承运行监测。Peng等[103]采用LPP对多个特征进行降维得到融合监测指标。Ma等[104]基于Grassmann流形下的LLE对多种优选统计特征进行融合得到监测指标。另外一种是基于非监督神经网络的重构方法,Huang等[105]采用自组织映射神经网络进行非监督降维得到最小量化误差作为监测指标,刘美芳等[106]、Hong等[107]和Zhao和Wng[108]均采用该指标实现了对滚动轴承的RUL预测。Guo等[109]基于单调性和相关性进行特征选择,并采用循环神经网络进行特征融合得到监测指标。
2) 监督指标
非监督指标的优势在于不需要失效数据,因为工作环境的不同,很难得到理想的失效参考特征,但因此带来的就是监测指标上限无法确定。而监督指标则基于健康数据和失效数据对监测数据进行度量,得到归一化指标,便于后续RUL预测。Wang等[40]采用模糊聚类方法对滚动轴承的各阶段损伤程度进行识别,并得到归一化监测指标。Pan等[110]采用SVDD度量测试样本到健康样本和失效样本的距离,然后结合模糊聚类实现滚动轴承的运行状态评估,监测指标如下
(5)
式中:μnormal为待测样本隶属于健康样本的隶属度,即为性能退化指标;dnormal和dfailure分别为待测样本到健康样本和失效样本的距离,并且当dnormal=0时,μnormal=1,说明待测样本处于健康状态,dfailure=0时μnormal=0,即为失效状态。其它改进算法有k-medoids聚类[111]、Gath-Geva聚类[112]和tight聚类[113]等。但是当全寿命轴承数据中出现愈合过程时,聚类方法的识别性能就容易出现问题,可能导致识别的同一类状态的区间没有连通在一起。
类似归一化模型还有逻辑斯蒂回归[114],可以看做模糊聚类的特例。另外结合MD,Wang等[66]构建了一种基于Sigmoid函数的归一化监测指标

(6)
陈俊洵[67]提出了基于双曲正切tanhx函数的归一化指标:
HI=1-αtanh(MD)
(7)

(8)
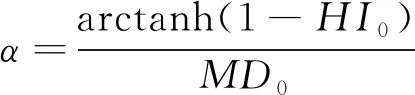
(9)
式中:HI0和MD0分别为初始时刻的监测值和MD。
通过上述分析可以看出,希望监测指标能够对性能退化的各个阶段进行准确表征,尤其是对早期故障敏感。但由于滚动轴承运行过程存在愈合效应,因此敏感性好的同时意味着波动性也会大,进而降低退化指标的单调性,使预测能力降低。针对提取特征的单调性不够明显、波动性较强以及特征存在反向同步性等特点,可以通过协整融合降低滚动轴承在运行前、中期由于愈合过程带来的长期波动性[115-116]。
2 预测算法
剩余使用寿命的各种定义如表3所示,一般以当前滚动轴承的使用状态为起点,结合直接表征工况的特征指标或者间接性能退化指标,预测从当前时间点到可使用寿命的结束点之间的时间长度,定义为

表3 剩余使用寿命定义
lk=tEoL-tk
(10)
式中:tEoL为可使用寿命;tk为当前运行时间点;lk为当前时刻的剩余使用寿命。
迄今为止,大量的RUL预测方法被学者提出,各种归纳分类如表4所示。RUL预测算法大致分为:基于概率统计的、基于模型的、基于数据驱动的,以及组合模型的预测方法。

表4 剩余使用寿命预测方法分类
2.1 基于概率统计的预测方法
由于加工精度、工作环境及安装误差等因素的影响,滚动轴承的疲劳寿命呈现分散性,即使通过标准试验条件也很难消除,因此需要概率分布对其进行建模分析。一般以L10寿命作为衡量标准,该寿命与具体单个轴承的实际工作寿命不会完全一致。考虑到工作载荷和滚子类型,多采用L-P理论对L10寿命进行计算,即

(11)
式中:C为轴承的额定动载荷;P为轴承的当量动载荷;ε为参数(对球轴承ε=3,滚子轴承ε=10/3);L10为可靠性为90%的轴承基本额定寿命,106转。
式(11)对应的修正公式为
Ln=a1a2a3L10
(12)
式中:a1为可靠性系数;a2为材料系数,包括材料、设计和制造等影响因素;a3为工作条件系数,包括润滑剂、润滑剂清洁度、逆向温度和装配条件等影响。在ISO推荐标准中,L10的涵义与上述理论基本相同,目前世界各国都遵从上述规定[131-132]。
另外,Heng等[133]基于Kaplan-Meier估计和总体全寿命退化数据对单体运行可靠性进行建模,并通过前馈神经网络预测单体退化路径进行实现单体可靠性预测。Feng等[134]基于威布尔分布的可靠度模型推导出单个轴承的在指定可靠度下的RUL预测模型。李永华等[135]对式(12)中影响轴承寿命的主要因素进行模糊化处,得到更接近于实际工况的寿命预测结果。覃楚东等[136]基于累计损伤模型和雨流计数法实现了风机发电机后轴承的磨损寿命预测,并通过油液检测和铁谱分析实验对结果进行了验证。
2.2 基于模型的预测方法
基于模型的方法需要借助数学或物理模型[137-138]对失效机理进行建模分析,建模精度取决于对其失效机理的了解程度,并且建模过程中无法考虑各种影响因素,因此最终得到的也只是近似解。实际工作中,很多装备工作过程的数学或物理模型获得是不经济甚至不可能的。
2.3 基于数据驱动的预测方法
近年来,随着传感器技术和信号处理技术的发展,可以较好的采集和处理滚动轴承在工作过程中产生的运行数据。利用这些反映滚动轴承运行状态的监测数据建立系统数学模型的方法,即数据驱动方法[139-140],已成为预测方法的主流。数据驱动的方法又可进一步划分为基于机器学习的方法[141-142]和基于不确定性的方法[143]。
机器学习算法包括浅层学习和深度学习,浅层学习包括人工神经网络如自适应神经模糊推理系统(ANFIS)[144-145]和极限学习机(ELM)[77,146-147]等,以及支持向量机[148];深度学习[149-154]包括深度置信网络(DBN)、卷积神经网络(CNN)、深度自动编码机(SAE)、循环神经网络(RNN)等。
由于大型设备系统运行机理复杂,系统各零部件之间相互耦合,加之恶劣工况,会导致采集的滚动轴承运行数据有强烈的噪声干扰甚至无法使用,而故障注入数据以及仿真实验数据的获取代价通常十分高昂。另外,其它工况下参考滚动轴承的历史工作数据往往具有很强的不确定、不完整和小样本等特性[155-156]。而机器学习中,ANN仅能给出RUL预测点的估计值,其预测结果不具备不确定性表达的能力,且对于小样本数据的预测能力较差。深度学习作为端到端的学习方式,在很大程度上摆脱了特征提取时的人为干涉与工程诊断的经验依赖,但在建模过程中仍有大量参数需要人工干预。同时,它也无法摆脱大样本训练的束缚,并且无法进行不确定性表达。
Vapnik[157]提出基于结构风险最小化原则的SVM,解决了小样本导致的学习不足问题,克服了人工神经网络学习方法中局部极小点和过拟合缺陷,具有优秀的泛化能力。最小二乘支持向量机[158](LS-SVM)采用二次项作为优化指标,并把SVM的不等式约束以等式约束代替,使求解SVM的凸二次优化问题转化为解一组线性方程组,降低了计算复杂性,加快了求解速度,提高了精度。基于贝叶斯框架的RVM[159]能够处理高维、非线性、小样本等问题,实现小样本下预测值的不确定性描述,具有良好的稀疏性、泛化能力与较高的预测精度。高斯过程回归[160](GPR)基于贝叶斯理论和统计学习理论,同样适用于处理高维数、小样本和非线性问题,其泛化能力强且与神经网络和支持向量机相比具有更易实现、超参数自适应获取以及输出具有概率意义等优点。由于核函数的选择对结果的影响较大,而核函数众多且可以组合生成新的核函数,这使得核函数的选择变得更为棘手。雷亚国[161]通过多种核函数随机权重组合的方法,对各种核函数扬长避短,得到了理想的RUL预测效果。Wilson和Adams[162]提出了一种新的核函数,称为谱混合核函数。该核函数涵盖一系列平稳核函数,能够有效避免在时间序列预测中核函数选择的问题。
不确定性方法包括统计回归方法[119]、模糊理论[163]和灰色模型[164]等,其中以统计回归算法为主,基于随机过程、统计推断等理论建立系统运行趋势的数学模型,不仅可以提供预测的点估计值,而且可以给出预测结果的概率分布。这对于PHM框架下的管理和决策活动,如备件订购和维修安排具有重要的现实意义。
2.4 基于组合模型的预测方法
上述预测算法各有使用条件的限制,需要根据失效机理认知程度和数据量的大小来选择合适的模型,具体步骤如图7所示[19, 165]。如果选择错误,就会导致计算结果产生巨大误差甚至失败[166]。

图7 预测方法选择
为避免主观的选择预测算法,可以采用组合模型的形式,使各类算法扬长避短。组合模型分为集成模型和混合模型。集成模型属于并列式数据处理方式,采用多个不同类型的预测模型分别进行寿命预测,然后再加权处理得到最终RUL结果[105]。而混合模型则属于串联式数据处理,在寿命预测的每个阶段采用最合适的模型,对模型能够扬长避短,包括物理模型和不确定性方法相结合,如裂纹扩展模型和粒子滤波(PF);或者数据驱动模型和不确定性方法之间的结合,如PF和ANN;数据驱动模型之间的混合,如高斯过程和神经网络;不确定方法之间的混合,如灰色理论和马尔科夫过程,以及其它组合等。
3 滚动轴承寿命预测
剩余寿命预测方法主要分为性能指标外推方法和参考度量方法。性能指标外推方法通过将单个滚动轴承的历史运行数据进行拟合,然后外推至失效阈值即可得到RUL的估计值或者预测区间。参考度量方法类似故障诊断,需要滚动轴承全寿命运行特征作为参考样本,并与当前使用轴承的运行特征进行对比,计算两者的相似性加权系数,进而通过对参考样本RUL进行加权实现运行轴承的RUL预测。
3.1 外推预测
外推预测方法将RUL定义为在当前时刻下还需要多长时间退化特征才能超过阈值,如图8所示。

图8 滚动轴承退化过程拟合示意图
定义式表达为
lk=inf(l:x(l+lk)≥γ)
(13)
式中:inf(·)为下确界;γ为阈值。
该方法需要考虑4个问题:1) 阈值的不确定性问题;2) 如何确定开始预测时间点的问题;3) 性能退化指标预测的不确定性表达;4) 由于滚动轴承运行过程中愈合效应的存在,性能退化指标呈现波动性,使得退化趋势与时间相关性差[167]。对于第1个问题,目前为止失效阈值并没有标准化的选择方法,只能通过专家知识指定,或者是参考其它滚动轴承的失效阈值。为便于计算,失效阈值通常被设置为固定值。但由于滚动轴承寿命的不确定性,使得失效阈值也是一个随机变量,因此即使在相同的工况下,也会导致参考样本和运行样本的失效阈值并不一致。对于第2个问题,一般都是基于3σ原则给出早期故障报警阈值,但故障报警时性能监测指标并没有明显退化趋势。只有当性能退化趋势发展到一定程度时,才能对其进行预测,但何时才能够开始预测仍然根据经验确定。基于此,Li等[122]根据3σ原则提出一种自适应选择开始预测时间点的方法。对于第3个问题,需要考虑预测模型、数据的不完整性和随机性等对预测结果的影响[155-156],而最终要得到的是不确定性程度最小的最接近真实值的RUL预测值。对于第4个问题,在轴承早期的退化过程中,由于滚动轴承的愈合效应,使得性能退化指标呈现较大的波动性,在退化趋势并不明显的情况下,通过递推式向前多步预测容易积累误差,导致预测结果严重偏离或者失效。围绕以上4个问题,以下主要介绍了基于数据驱动算法的滚动轴承外推预测方法,分为机器学习算法或者不确定性算法两部分。
3.1.1 机器学习算法
该类算法主要是指利用ANN或者SVM的方法对单个轴承的历史运行数据进行拟合和外推,进而实现未来趋势的预测。
在ANN的预测应用方面,Javed等[63]采用了总和小波-极限学习机,该模型是一种无调优单程的单层前馈网络,并且隐层节点参数独立于训练样本且相互独立。柏林等[69]采用了广义回归神经网络,该模型是以非参数估计为基础,具有很强的非线性映射和泛化能力以及高度的容错性和鲁棒性,适用于解决非线性问题。在深度学习中,CNN偏重于于分类,而循环神经网络则偏重于趋势预测,包括长短时记忆递归网络[168-169]、门控递归单元网络[53, 170-171]和双向门控递归单元网络[172-173]等。Chen等[174]提出量子循环编解码神经网络并引入注意力机制用以构建同时构建编码器和解码器,从而得到长时间序列信息的相关特征,提高预测的泛化能力。和门控递归单元网络、改进的共生生物体搜索极限学习机、遗传优化支持向量回归和深度神经网络循环编码-解码相比,该方法的均方误差收敛速度最快,预测误差最小。于重重等[175]采用了时间卷积网络对滚动轴承运行状态指标进行了预测;和长短时记忆递归神经网络、门控递归单元网络相比,时间卷积网络的预测误差最小。
SVM[49, 74, 99, 176]和LSSVM[37, 72]能够针对小样本数据进行预测,基于贝叶斯框架的RVM[177]则能够实现小样本下预测值的不确定性描述。Hong等[178]基于GPR实现了滚动轴承性能退化指标的不确定性推断,并得到失效阈值对应的失效寿命及其概率分布。
3.1.2 不确定性方法
该类算法通过随机过程和统计推断等数学理论建立预测模型,给出RUL的点估计值或预测区间[119]。Wang等[179]采用权值约束稀疏编码和稀疏线性自适应回归对性能退化指标进行外推,取得了极其精确的结果。Li等[42]基于长相关方法提出了基于混沌时间序列的轴承信号强度预测模型。李洪儒等[180]以广义数学形态颗粒值作为退化指标,通过灰色预测值与马尔科夫预测值求和的方法得到指标外推的预测值。Meng等[41]则以微分经验模态分解的前两个本征模态函数的分形谱参数为性能退化指标,同样采用灰色模型和马尔科夫过程结合的方法实现指标的预测。随机过程主要有Wiener过程模型[181]、Gamma过程模型及逆高斯过程模型等。王小林对Wiener随机过程建模中存在的非线性问题、测量误差、偏态问题和多元问题进行了研究和改进[14]。Hu等[182]采用Wiener过程对风机滚动轴承的RUL进行了预测。Wen等[183]采用了非线性Wiener过程进行滚动轴承RUL预测。Wang等[184]采用Wiener过程结合卡尔曼滤波实现了RUL及其概率分布的预测。金晓航等[185]则采用轴承两个垂直方向的振动信号构建二维Wiener过程,预测精度优于一维Wiener模型。Song等[186]研究了分数布朗运动在滚动轴承RUL预测中的应用。Li和Liang[187]对分数布朗运动中Hurst指数的估计方法即重标极差分析进行了改进,在滚动轴承性能退化指标预测中。Zhang等[188]则提出了一种考虑寿命和状态依赖性的长相关性退化模型,该模型更具有普遍性。
3.2 参考预测
参考预测方法基于滚动轴承的总体全寿命历史数据,通过对测试样本的加权实现个体的RUL预测。该方法无需指定失效阈值,且具有较好的长程预测能力和鲁棒性[189]。根据预测方法的不同,可以分为以下两种:
1) 是性能退化路径的模式对比,该方法需要解决3个问题:性能退化路径的建模、相似性比较的时间区间和相似性的度量,其中相似性度量包括欧式距离[190]、MD[184]、动态时间弯曲[191]和Frechet距离[192]等。张彬[62]提出基于函数主元分析的退化路径建模,通过均方差进行相似性度量实现了RUL的预测。Wang等[190]通过监测数据与历史数据的综合相似性分析,构建寿命比例调节函数,动态修改状态矩阵模型的参数,实现了对监测轴承寿命的自适应预测。Zhang等[191]将滚动轴承退化阶段曲线作为训练样本带入支持向量回归模型进行训练,得到测试轴承的RUL。孟文俊等[192]通过相空间重构技术实现当前退化过程和历史退化过程的对比,得到了滚动轴承的寿命预测值。
2) 是通过参考样本对预测模型进行训练,将测试样本带入训练好的模型实现单体滚动轴承RUL的预测。为减少性能退化指标波动性对RUL预测的影响,可以采用累加方法[97]、趋势提取[107]和曲线拟合[193]的方法对其进行平滑处理,然后将平滑指标作为训练样本带入机器学习算法进行训练。
基于神经网络的预测方法中,Rai等[97]采用马氏距离进行信息融合,然后对指标累加处理,将累加指标和对应的轴承寿命代入外生输入的非线性自回归神经网络进行训练,得到测试轴承的RUL。杜占龙等[147]采用多分类概率极限学习机估算运行设备在当前时刻分属不同设定退化状态的概率,将此概率值作为对各设定状态对应剩余寿命的加权值,实现当前设备的RUL预测。Ben Ali等[194]为消除滚动轴承愈合过程波动性对预测的影响,通过威布尔分布浴盆曲线对全寿命退化特征进行光滑处理,并指定相应的损伤程度,将其代入简化模糊自适应共振理论映射神经网络进行训练,即可得到测试轴承在实际数据下的退化程度,然后对各退化程度对应的RUL进行光滑拟合即可得到测试轴承的全程RUL预测。Ren等[195]提取Spectrum-Principal-Energy-Vector特征对深度卷积神经网络进行训练,利用正向预测数据对得到的预测数据进行线性平滑,进而得到连续的RUL。Tao等[196]针对滚动轴承截断数据的情况,采用流形学习的累积测地距离进行外推得到失效时间,并采用智能乘积极限估计器估计存活概率;然后将流形学习的邻近测地距离和存活概率分别作为前馈神经网络的输入和输出进行训练,最终实现测试轴承的RUL预测。张继冬等[197]将振动加速数据及对应的寿命比(单个轴承的剩余寿命与全寿命的比值)作为训练样本带入全卷积层神经网络,实现了测试轴承的RUL预测。该方法能够实现特征的自主学习,减少在特征提取和选择方面人工的干预。
基于支持向量机的预测方法中,康守强等[74]将两组滚动轴承全寿命数据提取的特征分别带入支持向量回归模型SVR1和SVR2进行训练,并互相验证,通过平均绝对误差、平均绝对百分误差、归一化均方误差和均方根误差得到两者的加权系数,进而实现了待测滚动轴承的RUL预测。Kim等[198]以轴承为研究对象,将其退化过程分为6个阶段,利用“一对一”多分类SVM方法进行故障分类,通过训练数据的分类情况求得轴承处于各个阶段的概率,最后利用轴承的工作时长和概率值预测剩余寿命。Peng等[65]采用高斯混合模型聚类将全寿命特征分为几种健康状态,代入LS-SVM进行训练,成功实现测试轴承的RUL预测。
在不确定方法方面,Liu等[199]基于对数线性递归最小二乘和递归最大似然估计,Lu等[200]基于变量遗忘因子递归最小二乘结合自回归移动平均模型均通过训练样本对模型进行参数辨识,并对测试轴承的RUL实现了预测。Zhang等[201]采用了和文献[194]相同的特征处理方法,将训练样本代入朴素贝叶斯进行训练,然后通过指数拟合各退化阶段的RUL即可得到测试轴承的全寿命预测。王奉涛等[75]利用IMS中心全寿命试验数据中的试验1和试验2数据,首先结合时域、频域和时频域特征构造高维相对特征集,其中7组作为训练数据;然后利用核主成分分析进行降维,将得到的核主元带入威布尔比例故障率模型进行训练,从而实现基于可靠度的单个轴承全寿命监测。何兆民和王少萍[202]首先将滚动轴承全寿命退化数据分为平稳退化、均匀退化、加速退化3种状态,采用具有时变状态转移概率矩阵的隐半马尔科夫模型对各个状态进行建模,得到各个状态的转移概率及持续时间;然后识别当前监测数据的健康状态并计算状态转移系数,最终得到滚动轴承的剩余寿命预测。Tobon-Mejia等[120]提出了高斯隐马尔科夫模型实现在线RUL预测,并给出了预测区间。张雨琦等[203]以对滚动轴承性能退化过程敏感的多个特征参数为基础,建立了多退化变量灰色预测模型对滚动轴承RUL进行预测。
3.3 组合模型
组合模型中集成模型主要采用加权的方式对各个预测算法的结果进行融合,使得各个算法能够扬长避短,得到的最终结果在各个状态阶段都更趋近于真实值[105, 204]。
混合模型也是借鉴各算法的优点,每个阶段采用最合适的模型进行建模,主要用于滚动轴承RUL的外推预测。在物理模型和不确定性方法的结合中,Lei等[205]利用Paris-Erdogan疲劳裂纹增长模型对滚动轴承的退化趋势进行建模,然后结合PF进行RUL预测;马波等[206]利用Paris公式描述疲劳裂纹稳定扩展规律,Foreman公式描述裂纹迅速扩展,结合PF进行滚动轴承的RUL预测;Qian等[61]基于递归图熵特征和AR(p)模型建立状态空间模型,结合卡尔曼滤波实现了滚动轴承的RUL预测;Lim和David[207]采用Ricatti模型建立状态空间模型,提出可以推断潜在过程并选择相应过滤器的转换卡尔曼滤波模型进行RUL预测。Qian等[208]采用加强相空间弯曲模型和基于时间分段算法改进的Paris裂纹扩展模型分别描述运行轴承的快尺度和慢尺度,实现了滚动轴承的RUL预测。在数据驱动模型和不确定性方法的结合中,包括自适应神经模糊和高阶PF的结合[145]、神经网络作为经验测量模型嵌入到PF中[209]、深度置信网络和PF结合[210]、回归模型和多层人工神经网络结合[211]、比例故障率模型和SVM[212]结合、RVM拟合相关向量,然后采用统计回归拟合[167]、以及指数回归和RVM结合[213]等。在数据驱动模型之间的混合如小波神经网络和高斯过程回归的结合[54]。在不确定方法之间的混合中,包括灰色马尔科夫[41, 180]、Wiener过程和卡尔曼滤波[184]、长相关模型和PF[214]、贝叶斯推断和高阶PF[215],半隐马尔科夫链模型和高阶PF[216]等。
3.4 迁移学习
由于使用条件的不同,不可能得到在所有工况下的滚动轴承全寿命数据。当采用其它工况下的全寿命样本作为参考时,就需要建立适当的模型进行迁移学习[217],通过寻找参考样本和测试样本之间的共同特征来实现RUL预测。Zhang等[218]首先分别从参考样品和测试样本的温度、扭矩和振动信号中提取特征,并采用PCA方法对多敏感特征降维,结合支持向量数据对这3个主成分分析指标进行进一步融合,通过归一化交叉相关法计算服务样本与参考样本之间的相似性,即可根据参考样品的RUL预测使用样品的RUL。Shen等[219]基于梅尔频率倒谱系数法建立滚动轴承性能退化曲线,通过传输压缩编码超平面分类器建立迁移学习模型,并结合指数半确定性扩展卡尔曼滤波器实现了多种工况下的滚动轴承RUL预测。Kundu等[220]提出了一种威布尔加速失效时间回归方法,在参数估计时能同时考虑工况参数和工况监测信号。
Zhu等[221]总结了目前RUL预测模型出现的问题:一是忽略故障发生时间或主观确定,不恰当的故障发生时间会引入不相关的信息如噪音,并削弱关键的退化信息;二是训练和测试数据遵循相同的数据分布,但由于不同工况数据分布上的差异,用一种工况下的数据集训练的预测模型,并不能很好地推广到另一种工况下的数据集。针对这两个缺点,Zhu等采用隐马尔可夫模型自动检测状态变化,从而定位故障发生时间。在此基础上,提出了一种新的基于多层感知器的转移学习方法来解决分布差异问题,最终实现RUL预测。
在深度迁移学习方面,Tan等[222]将其分为基于实例、基于映射、基于网络和基于对抗。针对滚动轴承的多种失效模式,Cheng等[223]利用CNN提取退化特征,然后在优化目标中引入多核最大平均误差,用以减小分布误差,最后经过训练迁移CNN实现测试轴承的RUL预测。Mao等[224]在线下训练时,利用皮尔森相关系数将滚动轴承退化指标分为正常状态和快速退化状态,将收缩去噪自适应编码提取希尔伯特-黄变换边际谱特征代入最小二乘支持向量机进行训练;进行在线RUL预测时,采用迁移成分分析循序调整测试样本和训练样本的差距,从而实现不同工况下滚动轴承的RUL预测。陈佳鲜等[225]利用时间卷积网络提取源域和目标域轴承退化序列的深度时序特征,并构建反映退化趋势的HI;然后以RUL退化序列为迁移对象,通过最小化序列相似度,构建面向时间序列的领域自适应算法,实现退化信息从源域到目标域的迁移;最后通过构建SVM回归模型实现了RUL的预测。
迁移学习在一定程度上解决了滚动轴承RUL预测中的样本数量问题,但参考样本的数量小、不完整和不平衡性等特性仍有待研究。
3.5 预测性能评估
上述方法均能够在一定范围内实现滚动轴承的RUL预测,但优劣难以比较和评价,这会导致在工程应用中选择模型时无法取舍,因此需要一定的标准对预测模型进行评估。国内外有关预测性能评价理论的相关研究[226],大致可以分为5个阶段:传统的基于误差的预测精度评价研究、预测有效性评价理论、损失函数法评价预测精度的研究、基于数理统计的预测手段有效性评价研究以及新兴预测性能评价指标。以下就应用最为广泛地基于误差的预测精度评估和新兴预测性能评价指标进行展开叙述。
3.5.1 基于误差的预测精度评估
滚动轴承寿命预测精度可表示为

(14)
式中:ta和tp分别为真实寿命和预测寿命。为评估上述方法在预测过程中的精度,采用如表5所示的指标进行衡量。

表5 预测精度评估指标
3.5.2 新兴预测性能评价指标
1) 2012年PHM会议中[28],采用式(15)计算各类算法在滚动轴承RUL预测性能方面的得分。通过得分大小来判断各类算法预测性能的优劣,得分越高,预测性能越好。

(15)
式中Er=100×(ta-tp)/ta。
2) Saxena等[227]提出5个评价指标,包括预测范围,α-λ准确度、相对准确度、累积相关准确度和收敛性。
预测范围定义为预测结果满足指定性能标准的首次时间和预测寿命之间的差值,表达式为
PH=tEoL-tiαβ
(16)
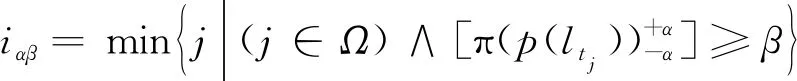
α-λ准确度定义为评估预测结果在指定时间索引下是否落在指定α-边界内的二元度量,表达式为
(17)
式中:λ为tλ=tFPT+λ(tEoL-tFPT)中的时间窗口调节参数,tFPT为首次预测时间。该指标表征的是时刻tλ时预测值相对实际值的准确度是否在规定的α-边界内。
相对准确度定义为

(18)

累计相对准确度定义为
(19)
式中:ω(ltk)为基于预测RUL的权重因子;Ωλ为从时刻tFPT到时刻tλ的所有索引;|Ωλ|为集合基数。累积相对准确度是对各相对准确度在时间上进行加权平均,反映的是预测准确度的总体情况。
收敛性用于表征某个度量的收敛速度,其值越小表示其收敛速度越快,定义为质心(xc,yc)和时刻(tFPT, 0)之间的欧式距离
(20)
式中:(xc,yc)为时刻tFPT到时刻tλ下Mk曲线覆盖区域的质心;Mk为度量预测准确度的时变非负值。
4 问题与展望
现阶段在实验室拥有大样本试验数据的情况下,深度学习算法对滚动轴承的故障特征提取、RUL预测、故障诊断及变工况下的迁移诊断和预测都取得了丰硕的成果。但实际中获得滚动轴承变工况小样本试验数据的情况居多,并且很多理论方法都是通过实验室数据进行验证,不足以充分说明理论研究的实用性和稳健性。相应的问题仍有待强化和改进,主要体现在:
1) 减少强噪声和相干部件的振动干扰。在非平稳、非高斯、低信噪比和各种谐波干扰的信号中提取滚动轴承的瞬态故障特征信息,实现滚动轴承的故障定位和损伤程度的识别,进而得到预测起始点和准确度更高、不确定性更小的RUL预测值。
2) 提取退化特征的多样性。滚动轴承振动信号中提取的退化特征多种多样,尺度不统一,单位不统一,盲目的特征降维和融合会导致性能退化指标具有不一致性。
3) 指标的标准化,如失效阈值的标准化,模型选择的评价指标等。标准化能够减少建模过程中的经验干扰,有助于预测模型的自适应调整,方便向工程应用推广。
4) 变工况下的寿命预测。由于工作环境的复杂性和工况需要,滚动轴承需要在变载荷变转速下工作,这会使得采集的参考样本数量较小甚至无样本。另外,历史参考样本数据还会有不完整、不平衡和无标签等特性,这些都会导致在新的工况下滚动轴承RUL预测不确定性增大甚至预测不准确。
对于未来滚动轴承RUL预测的发展,可以从以下几个方面着手:
1) 向高维度方向发展。高维特征和张量特征可以考虑多维度的影响因素及其相关性,同时减少噪声的干扰,利于性能监测指标的构建和RUL预测。
2) 向自适应方向发展。譬如复杂性度量中熵值的计算,监测指标的失效阈值确定,以及预测模型的参数等都需要进行参数指定。如果能够制定相应的优化标准,就能够对参数进行实时辨识,减少经验的干扰。
3) 无监督深度迁移学习在滚动轴承RUL预测中的应用。由于机械装备的更新换代,使得滚动轴承经常在不同的工况下工作,并积累了大量的参考样本。但样本常常不完整,并且没有标签化,因此无监督深度迁移学习的研究应用将极大提高参考样本的价值。
4) 具有通用性的PHM平台搭建及其标准化。平台的搭建,不仅可以把滚动轴承的PHM管理作为模块与其它框架共融,还可以把滚动轴承RUL预测的理论研究拓展到其它零部件的研究。
5 结束语
滚动轴承RUL预测方法的研究将极大推动机械系统关键零部件全寿命周期可靠性设计理论的发展,形成更加完善的健康管理框架体系。文中对滚动轴承RUL预测所涉及的主要模块如信号降噪,特征提取、降维和融合以及监测指标的构建进行了详细的阐述。基于对滚动轴承损失机理和数据量大小,对预测模型进行了分类并给出选择流程。根据预测形式的不同,将预测方法分为性能指标外推预测方法和参考预测方法,并给出预测方法的评价标准。最后对滚动轴承RUL预测中出现的问题进行梳理。在此基础上,对滚动轴承RUL预测未来的发展趋势和方向进行了展望。
