两栖仿海龟机器人步态规划及分析
2023-02-16芮宏斌李路路曹伟
芮宏斌, 李路路, 曹伟
(西安理工大学 机械与精密仪器工程学院,西安 710048)
水土流失导致的底泥清淤问题日渐成为国内外疏浚行业关注的焦点,我国和美国为此投入了大量的人力和物力[1-2]。为了提高清淤效率,各国均研制出不同的清淤机器人。支撑和移动的稳定性是清淤机械面临的首要问题,芬兰的“水王”清淤船[3]作为行业标杆,虽然可以通过船尾的定位桩在水中支撑,但是它在移动时船体始终与地面摩擦,通过性差。海龟作为一种两栖爬行动物经常从水中爬向沙滩,它通过足部和身体分别支撑地面依靠四肢向前爬行,能够在松软的沙地上稳定站立和移动。仿海龟机器人具有很高的抗倾稳定性,发展前景广阔。
近年来,国内外出现了各种仿海龟机器人,其中日本大阪大学的Kawamura等设计出了一种名为“RT-I”的两栖式机器人,该机器人同时模仿了海龟和陆龟的运动模式,分别具有在水中基于升力游泳和在陆地四足爬行的移动方式,主要用于自然海岸和滩涂环境的自动检测;但是该机器人支腿没有较大的承载能力,只能承担自身的80 kg质量[4]。南洋理工大学的Low等参考海龟科动物在水中和陆地上的运动行为,设计出了一种机器海龟,实现了其有效和稳定的游泳能力;但是该机器人侧重于水下的运动,其设计原理难以胜任陆地或沼泽地的移动[5]。上海交通大学机器人研究所参照生态龟的结构形态和运动形式,设计了一种能够实现水陆两栖爬行的“四足两栖机械龟”,具有良好的稳定性;但是该机械龟的支腿是一个简单的四连杆机构,关节铰点较多,大大降低了机械龟的承载能力[6-7];哈尔滨工业大学针对所创作的机器人戏剧剧本,设计出了一套用于数字舞台表演的大型海龟机器人系统,并为其规划了相应的四足协调步态;但是该机器人的动作,如:龟壳开合、柔性脖子伸缩等,仅适合用于观赏性的舞台表演,难以在复杂的实际工程中应用[8-9]。
本文以海龟为原型,设计了一种两栖仿海龟机器人,整机结构与海龟的身体结构相似,每条支腿有两个主动自由度,可仿海龟爬行。通过研究海龟的爬行动作,为机器人规划相应的爬行步态,并根据足端轨迹进行步态优化;通过运动仿真验证步态的正确性,根据结果对机器人步态做出评价。
1 机器人的结构设计
通过研究海龟的身体结构,设计了一种两栖仿海龟机器人,其三维模型如图1所示,包括机体和4条支腿,分别对应海龟的身体和四肢,每条支腿由沼泽轮、支撑腿和转架组成,动力由支腿缸和转腿缸两个电推缸提供。

图1 两栖仿海龟机器人的三维模型
机体的前端设计有一转盘,可以在此处安装挖掘臂、机械手等部件来进行各种实际工程作业,机器人的主要结构参数如表1所示。
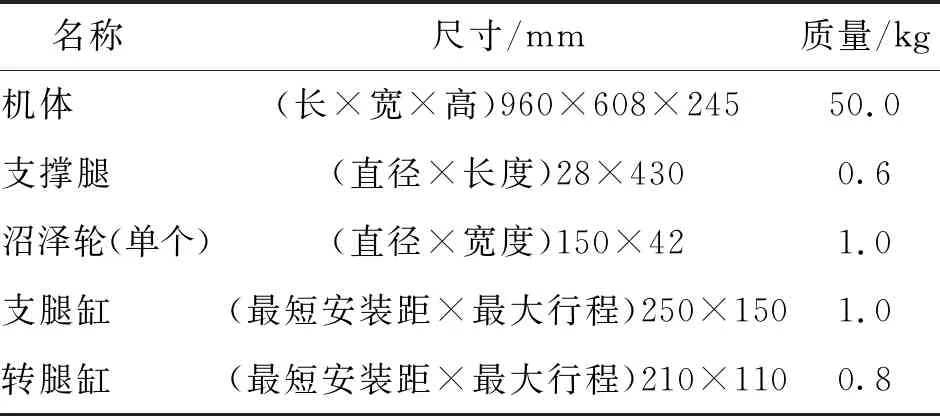
表1 两栖仿海龟机器人的主要结构参数
两栖仿海龟机器人是一个多刚体系统,4条支腿采用正向对称布置的方式。每条支腿具有两个主动自由度:① 支腿缸负责放腿和抬腿,可以将上机抬起和落下,其缸体端和推杆端分别与转架上铰点和支腿中部铰接,推动支腿绕转架的下铰点上下转动,支腿缸活塞完全缩回(或伸出)时,沼泽轮会悬空(或支撑地面);② 转腿油缸负责爬行和摆腿,其缸体端和推杆端分别与机体和转架侧面铰接,推动支腿绕机体一角水平转动,转腿缸活塞完全缩回时,4条支腿与机体纵向平行。
支腿上的沼泽轮为自由轮,由两个普通轮胎组成,通过销轴连接在支撑腿的末端,这样的布置提高了机器人的稳定性和对复杂地形的适应能力:当机器人抬腿和放腿时沼泽轮在地面上滚动,大大减小了与地面的摩擦力;爬行时轮胎受到地面侧向力作用,胎顶与地面摩擦,胎侧与松软土壤相互挤压,为机器人的爬行提供推力。
图1中的机器人支腿结构与其他仿海龟机器人的支腿相比,关节数量更少,机器人的重量和运动负载将由一根完整的杠杆承担,受力情况更好,提高了支腿的负载能力;并且4条支腿具有更加离散的地面支撑,使机器人获得了更大的支撑域,因此两栖仿海龟机器人具有更高的抗倾稳定性,对复杂地形的适应性更强,支撑和移动的可靠性更高。
2 运动学分析
多刚体系统的运动学分析是将机构空间的位移量解析表示为时间的函数,对于两栖仿海龟机器人,其爬行过程中沼泽轮的位置姿态与支腿关节的变量空间有关[10]。对机器人进行运动学分析,建立方程求解在电推缸的驱动下,机器人支腿的位姿变化。
2.1 坐标系统建立
以右前腿为例,对两栖仿海龟机器人进行运动学分析,将转架与机体、转架与支撑腿的铰接点分别视为关节1和关节2,将基准坐标系{0}建立在转盘的中心,X0OY0平面与转盘的上端面重合,X0轴正向为机器人的前进方向,Y0轴指向机体侧面,Z0轴正向为重力的反方向。利用D-H方法[11-12]建立如图2所示的坐标系,其中关节1和关节2的中心线分别与Z2轴和Z3轴重合,Z3轴与Y2轴平行,且与转架侧面垂直;X2轴指向关节2(坐标系{3}),X3轴指向沼泽轮(坐标系{T})。假设关节1和关节2的关节变量分别为φ和ψ,基准坐标系{0}与坐标系{1}的原点在X0向和Y0向的距离分别为L1和L2,坐标系{1}、{2}、{3}、{T}的距离分别为L3、L4、Lrf,定义足端沼泽轮在基坐标系{0}中的位置为0B=[BXBYBZ]T,则从坐标系{0}到坐标系{T}的变换矩阵为:
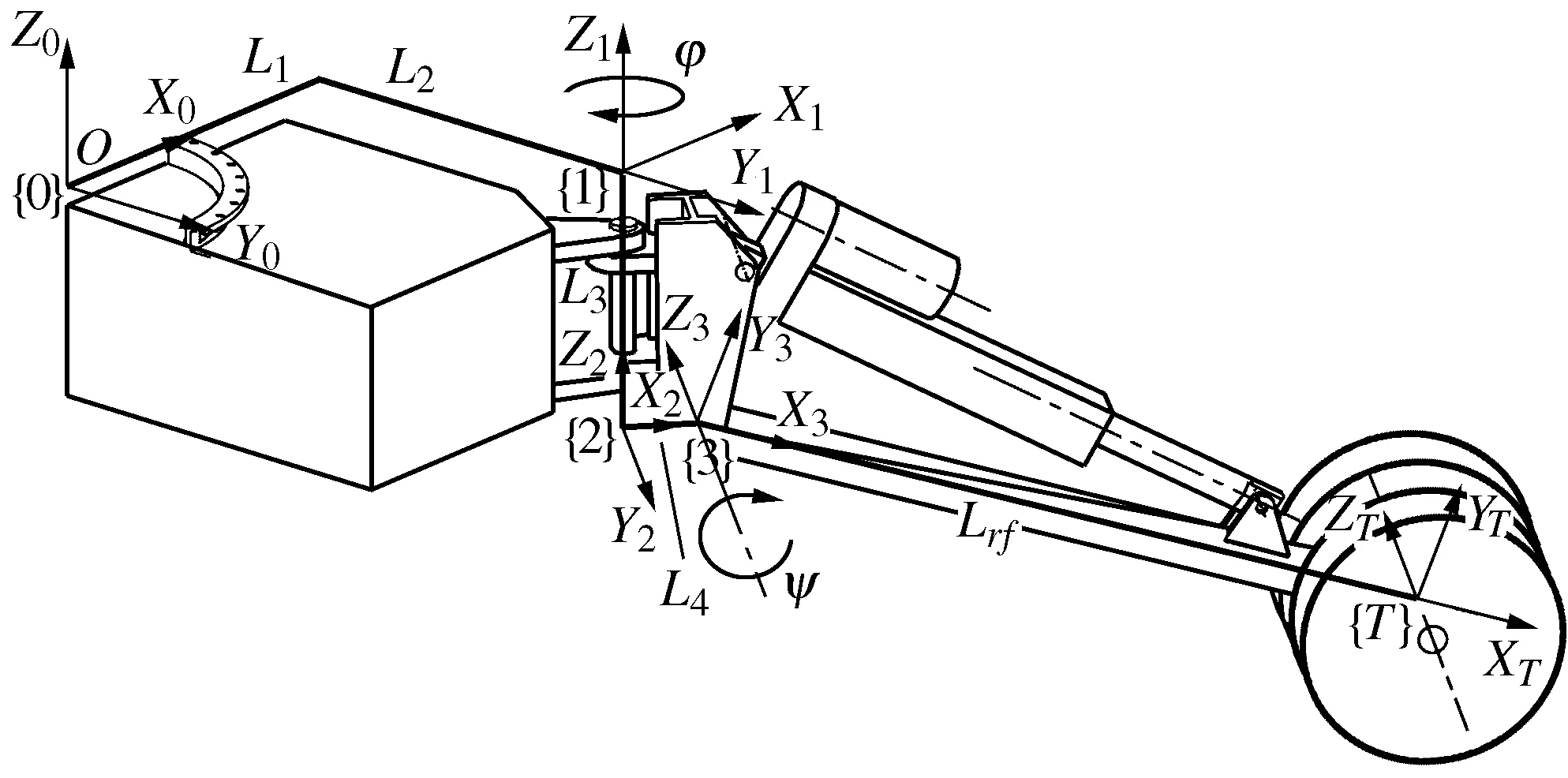
图2 机器人右前腿坐标系
则足端沼泽轮在基坐标系{0}中的坐标可表示为:
(2)
式(2)代表足端在基坐标系{0}中的位置坐标与关节变量之间的映射关系,由此可以建立机器人支腿的雅可比矩阵为:

(3)
雅克比矩阵可以表示操作空间和关节空间之间的速度映射关系和力的传递关系[13],则由式(3)可得,足端在基坐标系{0}下的线速度P*为
P*=J(θ)θ*
(4)
式中θ*为关节的操作速度。
2.2 坐标系统求解
现分别对支腿的起升运动和爬行运动进行分析,求解支腿缸的工作行程SI和转腿缸的工作行程SH对关节变量ψ和φ的映射关系。同样以右前腿为例,各坐标系和关节变量已在图3和图4中画出,其中:P点和A点分别代表坐标系{2}和{3}的原点;Lrf为支撑腿的长度;h*指出了机体底面的位置;R为沼泽轮的半径;Irf和Hrf分别为支腿缸和转腿缸的两端长度,其换算关系为:

图3 支腿的起升运动简图

图4 支腿的爬行运动简图
(5)
随着支腿缸推出,支撑腿绕A点顺时针转动,根据余弦定理,关节变量ψ可表示为:
(6)

(7)
式中ξ等于∠BAD加上AC与Z2轴正向的夹角。
随着转腿缸推出,整个支腿绕P点顺时针转动,同理可得关节变量φ可表示为:
(8)

(9)
式中:η为FP与X2轴正向的夹角加上PE与Y1轴负向的夹角;ξ和η为固定值,只与支腿结构有关。
将式(5)~式(9)代入式(2)中,即可得到两栖仿海龟机器人的正向运动学方程,结合表1中的数据即可得到机器人右前腿足端的工作空间,如图5所示。
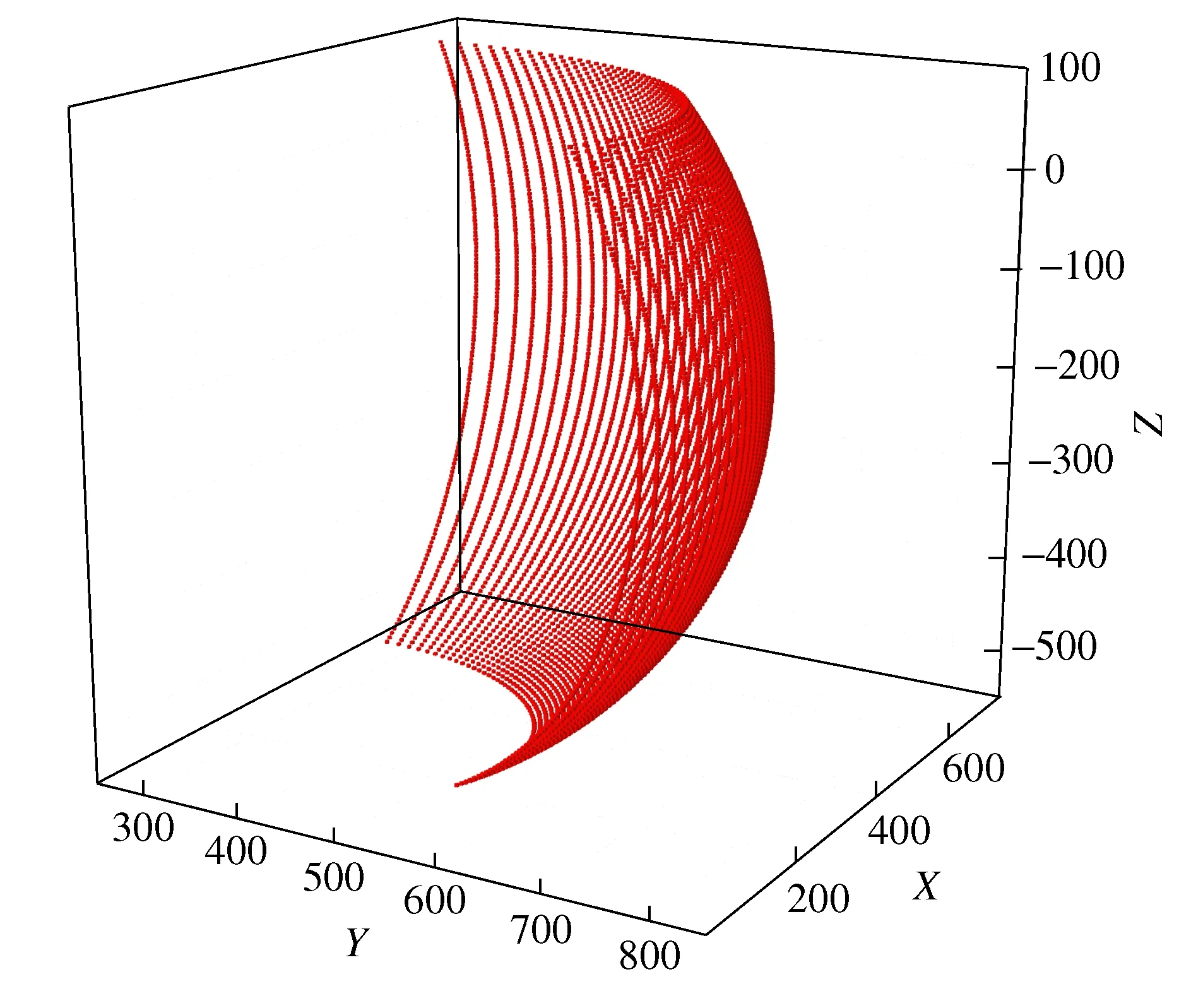
图5 右前腿足端的工作空间图
3 步态规划
3.1 动作规划
海龟在平地上爬行时,它的四肢和身体交替支撑着地面,具有很高的抗倾特性。我们通过观察,将其爬行动作顺序分解为放腿、爬行、抬腿和摆腿,其中放腿表示四肢竖直下压将身体抬起;爬行表示足端与地面相互作用的移动动作;抬腿表示四肢将身体落下支撑地面,直至足端悬空;摆腿表示身体支撑地面,四肢悬空水平摆动的动作。根据如上动作,规划了如图6所示的步态顺序,其中0、1分别表示足端或机体的支撑相和摆动相。

图6 海龟爬行步态顺序图
根据如上步态顺序,设计了两种两栖仿海龟机器人的爬行步态,按照其爬行阶段转动支腿的数量可分为两腿爬行步态和四腿爬行步态,前者只需前两条支腿爬行转动,后两条支腿始终与机体纵向保持平行,只起到支撑作用,并配合前腿做放腿和抬腿动作即可,如图7a)所示;后者要求机器人的4条支腿同步动作且始终保持前后两两平行,如图7b)所示。

图7 机器人爬行步态简图
本文以四腿爬行步态为例,研究并分析两栖仿海龟机器人的爬行运动。首先由机体支撑地面,4条支腿摆动到实线位置;支腿将机体撑起后,转动到点划线位置,表示机器人爬行一次;最后机体下落再次支撑地面,支腿悬空摆动到下一次爬行的初始位置(虚线),重复这个过程机器人就可以连续向前直线爬行。在这种爬行步态中,每条支腿的单次动作都只由一个电推缸驱动,因此单条支腿不存在冗余驱动的问题,增加了电推缸的驱动效率。
3.2 电推缸的工作行程规划
为了满足前文中规划的步态,需要求解SI和SH的行程空间,即对两种电推缸的工作行程进行规划。对于四腿爬行步态,其前后支腿需要时刻保持两两平行,则有
φf=180°-φr
(10)
式中:φf和φr分别表示前、后支腿关节1的转角。为了增大机器人单次爬行的距离,将图7b)中实线位置的后转腿缸伸出到最大长度,即Hr=320 mm,由式(8)~式(10)计算得,此时前转腿缸的长度为Hf=287 mm,则限制转腿缸的工作行程为SH∈[77,110]mm。
考虑到h*=108 mm,则机体支撑地面时有
R+Lrfsinψ≤h*
(11)
由式(6)、式(7)及式(11)计算得,支腿缸的两端长度I≤315 mm时,是机体在支撑地面,沼泽轮悬空。为了使机器人爬行得更加平稳,将机器人上机的离地高度限制在40 mm以内,计算得Imax=325 mm,则限制支腿缸的工作行程为SI∈[55,75] mm。以上计算中所用的支腿结构参数如下:L1=216 mm,LAC=102 mm,L2=306 mm,LAD=327 mm,L3=153.5 mm,LEP=270 mm,L4=42 mm,LFP=68 mm,ζ=20°,η=65°。
3.3 足端轨迹规划
为了提高机器人的移动速度和机身的稳定性,需要对机器人足端轨迹进行规划,防止关节出现速度突变引起较大的碰撞力,导致机器人失稳。本文采用改善的关节空间法在X0OZ0平面内对机器人的足端轨迹进行规划,并采用五次多项式插值对电推缸的工作行程进行插补,具体步骤如下[14]:
1) 确定电推缸的行程空间;
2) 对电推缸的行程变量进行插补,得到光滑的工作行程变化曲线;
3) 根据正运动学方程,带入并求解机器人足端轨迹。
根据沼泽轮的悬空和触地状态,将每一个步态周期分为摆动相和支撑相,两段轨迹首尾相连,摆动相从机器人的抬腿点开始,到落脚点结束,支撑相则与之相反。以右前腿的摆动相为例,对机器人的足端轨迹进行规划。定义插值多项式为
F(τ)=a0+a1τ+a2τ2+a3τ3+a4τ4+a5τ5
(12)
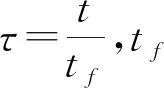
将电推缸的行程变量表示为
S(t)=Sb+(Se-Sb)F(τ)
(13)
式中:Sb和Se分别表示起始点和落脚点电推缸的工作行程,即3.1中的工作行程规划。
为了让机器人支腿和机体运动平缓、稳定,定义约束条件为:
(14)
联立式(12)~式(14)式,求解得到:
a0=0,a1=0,a2=0,a3=10,a4=-15,a5=6
(15)
将以上数据代入式(13)中,即可得到电推缸的行程变量表达式,同理可得到整个步态周期的电推缸的工作行程变化曲线,如图8所示,将表达式代入正运动学方程中,即可得到机器人足端的最优轨迹,如图9所示。

图8 电推缸的工作行程变化曲线
4 运动仿真及结果分析
4.1 运动仿真
在ADAMS中对机器人的爬行运动进行仿真,电推缸和关节铰点分别通过移动副和转动副约束,以右前腿为例,采用位移控制模式,为了看出足端轨迹规划对机器人移动速度和稳定性的改善,设置了一组对照仿真,对照组为未规划前的步态,其驱动采用简单的STEP阶跃函数定义,驱动曲线如图10所示。而实验组则采用了图8中的驱动函数,两组电推缸活塞杆的伸缩速度一致。为了在ADAMS中定义插补后的电推缸行程变量表达式,利用了嵌套的IF函数定义时间范围,MOD函数定义周期并使函数循环调用,这样只需要定义一个周期的支腿动作,机器人就可以一直爬行。

图10 对照组的驱动函数
考虑到仿真过程的非稳态情形和精度要求,机器人的轮胎和路面模型选用UA轮胎和Flat路面,查阅相关资料,轮胎的参数定义如表2所示[15]。设定End time为18 s,Step size为0.1,开始运行仿真,仿真动画如图11所示。
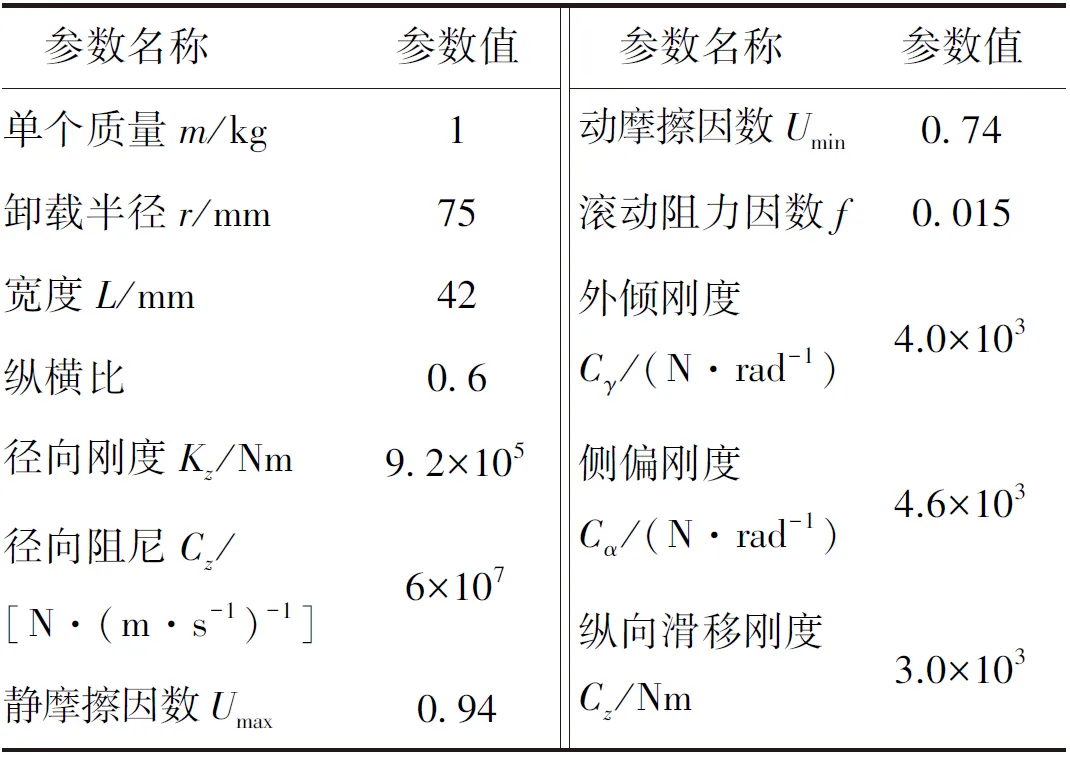
表2 UA轮胎参数表

图11 仿真动画图
4.2 结果分析
通过运动仿真得到两组运动数据,经过数据处理,绘制机身的位移、速度及电推缸输出力的对比曲线,如图12、图13和图14所示,其中X向、Y向和Z向分别代表机器人的纵向、横向以及竖向。

图12 机身位移曲线

图14 电推缸输出力曲线
由图12~图14可得,在18 s内,对照组爬行了3个周期,而实验组爬行了6个周期,这是因为足端轨迹规划后,将放腿和爬行动作同时进行,抬腿和摆腿动作同时进行,优化后的步态的占空比达到了2/3,而普通步态的占空比只有1/3,故而在活塞伸缩速度相同的情况下,前者每个步态周期的时长更短。
由图12a)得:实验组的平均速度大于对照组;在18 s内,前者前进了1 749 mm,平均速度为97 mm/s;后者前进了883 mm,平均速度为49mm/s,仅为实验组的一半。并且由图12b)可以看出:实验组在6次爬行后,在横向仅偏移了0.64 mm,与机体总宽608 mm相比,波动率为0.1%;对照组爬行了3次,产生了4.9 mm的偏移,波动率为0.8%,两组爬行在横向都十分平稳,但是实验组达到了更优的效果。图12c)表示了机体在竖直方向上的起伏,最高为42 mm,与3.2节中所规划的接近。
通过图13可以观察到机体在各个方向上波动的速率,可以发现对照组在X方向上,其图像每个周期都会产生两个波峰,说明每次爬行都会向前晃动一次,分析在于前后转腿缸的协调性导致,实验组则没有产生这种现象,说明各电推缸的协调性较好。图13b)中对照组的图像有较大的超调量,且呈发散趋势,说明继续爬行下去,机体的横向偏移会更大;而实验组的图像十分稳定,横向波动速度几乎为0。两组在Z方向上的波动速率都十分规律且平缓,说明竖向没有对机体产生过大冲击或振动。
图14是机器人右前腿的支腿缸和转腿缸的输出力曲线,可知实验组转腿缸的输出力明显小于对照组,且图像规律,没有发生突变,最大不超过200 N;支腿缸输出力最大为800 N,可为电推缸的实际选型提供理论依据。综上所述,足端轨迹规划不仅增大了机器人的前进速度,大大减少了横向偏移;而且提高了机身的稳定性,让机器人在纵向和横向的波动更加平稳;并且在活塞杆伸缩速度相同的情况下,降低了转腿缸所需的输出力。
5 结论
1) 以海龟为原型,设计出了一种两栖仿海龟机器人,通过理论和仿真验证,证明机器人机械结构合理,具有更高的抗倾稳定性。
图4(a), 4(b)分别给出了30°压缩拐角(模型3)在I, II线上的计算压力和实验结果的分布对比. 在平板干扰区内, 计算和实验也符合较好, 数值计算的分离范围略小于实验结果. 在楔面上, 计算压力与实验值的大小比较接近, 但是峰值位置有一定的差距. 虽然30°压缩拐角模型网格量要远大于20°压缩拐角模型(见表1), 但是计算精度没有得到提高.
2) 通过研究海龟的爬行方式,为机器人规划出两种爬行步态;并利用关节空间法规划了足端最优轨迹,得到了最优的四腿爬行步态。
3) 最后对普通步态和优化步态做了对比仿真,结果表明足端轨迹优化可以大大提高机器人的爬行速度和稳定性。
