原位测量软材料弹性模量的光学相干弹性成像方法研究

陈金龙，潘 航，林祥龙，胡永政，孙翠茹，邱文豪

原位测量软材料弹性模量的光学相干弹性成像方法研究

陈金龙1, 2，潘 航1, 2，林祥龙1, 2，胡永政1, 2，孙翠茹1, 2，邱文豪1, 2

(1. 天津大学机械工程学院，天津 300354；2. 天津市现代工程力学重点实验室，天津 300354)

弹性波光学相干弹性成像是利用波速定量获得生物组织弹性模量的方法，在医学研究与疾病诊断的领域具有重要应用价值．目前利用瑞利波理论评估一定厚度软材料的弹性模量存在较大的测量误差．为了提高弹性模量测量的准确度，提出了一种基于瑞利-兰姆方程反求弹性模量参数的方法．根据瑞利-兰姆方程的数值解，在确定仿体厚度的情况下，匹配合适的激励频率测量并获得弹性模量，将原位测试的弹性模量与拉伸实验结果进行比较，发现相对误差在3%以内．通过双层仿体的频散实验发现，在匹配的激励频率下，原位测量的弹性模量与拉伸实验测量的弹性模量几乎一致，结果表明该方法在测量上层仿体时不受下层仿体的影响．通过真实猪皮组织测量，结果表明该方法可以适用于皮肤组织测量．本研究提出的原位软材料光学相干弹性测量方法可以为生物组织的弹性定量表征提供更准确的测试手段．

弹性波；光学相干弹性成像；瑞利-兰姆方程；弹性模量

皮肤癌[1]、心血管疾病、乳腺癌等生物组织疾病严重危害人类的健康及生活质量，识别其生物组织力学性能的变化是早期精准治疗的关键．传统测量生物组织的力学方法如拉伸[2]、压缩等无法实现在体的定量表征．弹性成像的出现为生物组织在体表征提供了新思路．弹性成像是能够测量生物组织弹性特性的方法．根据检测组织响应的方法可以分为超声弹性成像、磁共振弹性成像以及光学相干弹性成像(optical coherence elastography，OCE)等[3]．得益于高分辨率的光学相干断层扫描成像(optical coherence tomography，OCT)的OCE技术在生物组织测量中具有显著的优势．OCE技术能够高精度地提取和评估组织变形的不同参数，以重建生物组织的力学特性[4]. OCE技术通常通过外部或内部激励生物组织，来测量相应的组织响应[5]．为了激励生物组织产生响应，目前常用的方法有机械接触式加载[6]、气吹非接触式加载[7]以及激光非接触式加载等[8]．其中，以压电换能器(piezoelectric transducer，PZT)产生弹性波的机械接触式加载方式在表征在体皮肤组织以及其他软材料的弹性参数方面有着巨大的潜力[9]．

PZT在激励过程中，不同尺寸的机械激励探头以及生物组织的厚度，会形成不同波速的弹性波．合适的探头参数以及物理模型是此方法参数反演的关键．对于单脉冲激励而言，产生的波速近似为横波波速，其与探头横截面尺寸近似满足如下关系[10]，即

式中：BW为机械波的带宽；S为横波波速；为探头截面直径．单脉冲加载具有低信噪比的特点，为了得到高信噪比的信号，通常采用连续加载的方式．但是对于连续加载而言，难以通过式(1)进行描述；同时，利用基于半无限空间假设的瑞利波理论[11]定量评估生物组织时，当被测生物组织的厚度达到毫米尺寸甚至更小，厚度对波速产生影响[12]，从而导致低频率激励测量得到的弹性模量被低估，而高频激励会导致信噪比减小．

目前利用PZT-OCE系统测量生物组织的弹性常数，包括弹性模量、黏弹性系数等比较普遍．但是在实际测量过程中往往忽略了激励探头尺寸对于波速的影响，同时也没有考虑被测组织的厚度对波速的影响，而直接利用剪切波与弹性模量的关系[9]或者瑞利波与弹性模量的关系[11]得到弹性模量，这导致在测量真实生物组织的弹性模量时存在较大的误差．因此在基于PZT连续加载方法中，需要探究新的方法来提高软材料测量的精度．

本文结合不同厚度生物仿体的实验结果，提出了基于瑞利-兰姆方程反求弹性模量的方法．通过探究探头的形状及尺寸对弹性模量测量结果的影响，选择合适尺寸的探头作为激励探头．之后，经过单层仿体与多层仿体的验证实验，证明提出方法的有效性．该方法能在确定仿体厚度的条件下，匹配合适的激励频率用于获取准确的弹性模量信息．

1 实验原理

1.1 理论基础

在实验中，生物组织仿体上表面与空气接触，下表面为自由面，沿着仿体传播的机械波称为导波．假设被测仿体是厚度为的板，如图1(a)所示．当板的上下表面应力为零，在均匀各向同性自由板中传播的导波为兰姆波[13]，如眼角膜表面传播的弹性波[14]．

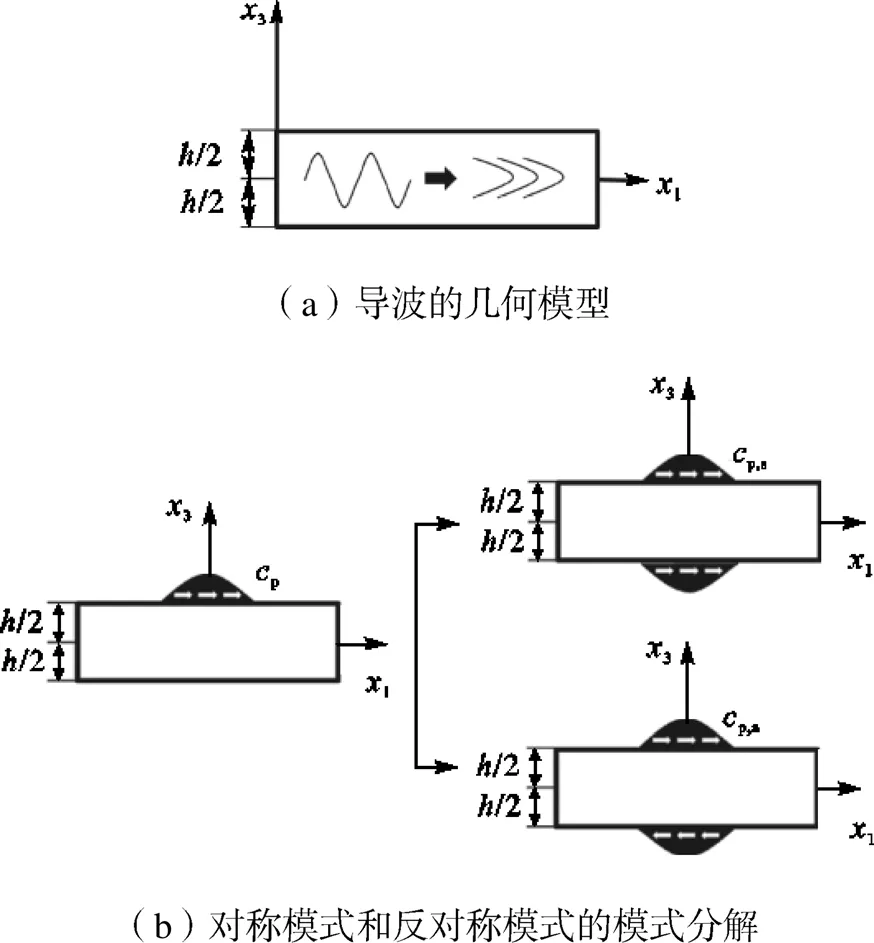
图1 导波传播的几何描述

弹性动力学的基本方程为

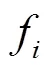
将亥姆霍兹(Helmholtz)分解的结果代入式(2)，可以得到两个解耦合的波动方程，即

式中：和分别是位移经过亥姆霍兹分解所得的势函数；1和3分别是笛卡尔坐标分量；为时间；L为纵波波速．假定式(3)的解为平面简谐波形式，如式(4)所示．

式中：是波数；是角频率．可使得求解的位移场与应力场表示为关于3＝0的奇(或偶)函数，并且能够分成两组模式，即对称模式和反对称模式，如图1(b)所示．对称模式中1相对仿体厚度中心是对称的，3是反对称的；反对称模式中3相对仿体厚度中心是对称的，1是反对称的．

在自由边界条件下，可得瑞利-兰姆方程，即

对于有限厚度的生物仿体中导波的传播问题可以表达为对称模式和反对称模式的解的线性组合．图2为＝1.16g/cm3，＝477.462kPa，＝0.48时瑞利-兰姆方程的数值计算结果，以频厚积为自变量，相速度p为应变量．忽略高阶模式下的影响，只考虑零阶对称模式和反对称模式．因此，在单层生物仿体中传播的波速p的表达式为

式中：是对称模式S0的相速度；是反对称模式A0的相速度；a 和β是系数．

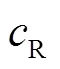
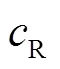
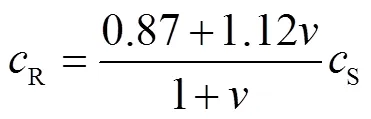
依据弹性模量与之间的关系，联立式(7)～(9)，可得波速与弹性模量的关系，即

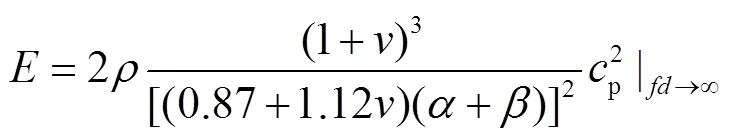
1.2 反演模型参数

为了确定式(10)中参数和，需要对不同厚度仿体进行测试．表1给出了不同厚度仿体测量获得的平均波速．通过瑞利-兰姆方程的数值解与实验数据进行拟合，可得＝1.93，＝－0.17，如图3所示．图3中黑色散点表示不同厚度仿体测量获得的平均波速并标明了方差带，黑色曲线表示瑞利-兰姆方程数值解的拟合曲线．根据拟合曲线，可以发现当厚度达到12mm时，随着厚度的继续增大，波速趋近于一个稳定值，该稳定值为(＋)R，即12mm处为曲线拐点．由于实验激励频率为1000Hz，因此仿体的频厚积为12kHz·mm．

表1 不同厚度仿体的实验数据

Tab.1　　Experimental data of the phantom with different thickness

图3 数值拟合曲线及实验数据

2 材料与实验设置

2.1 实验装置

PZT-OCE系统包括2个组成部分：激励装置和OCE系统，如图4所示．激励装置主要是由信号发生器(DG4202，RIGOL)、信号放大器(ATA-2021H)、压电堆栈(PK2FMP2，Thorlabs，美国)、探头以及三向位移平台(561D ULTRAlign Stage，Newport Research)构成．三向位移平台的位移精度为10μm．压电堆栈与探头通过黏结的方式连接，压电堆栈的另一端固定在三向位移平台上．OCE系统使用高速扫频激光源(HSL-20-100-B，santec)，扫描频率为100kHz，激光源是平均功率为18mW、中心波长为1310nm、带宽为80nm的近红外光．近红外光经过90/10耦合器分离后，10%的近红外光进入参考臂；90%的近红外光进入样品臂，经过电流振镜(GVS002，Thorlabs)和36mm焦距的聚焦物镜(LSM03，Thorlabs)后聚焦到被测生物仿体表面．样品臂与参考臂反射回来的激光经过50/50耦合器发生干涉．光电探测平衡器采集干涉信号并传输到计算机的采集卡(U5303A，Keysight Geneva)中，OCE系统以M模式运行：在任何特定的横向位置处获取采集点在一个完整时间序列的响应信息，采集点沿纵向由1024个像素组成．通常情况下，一个时间序列的长度为10ms，可利用Labview软件进行设定．

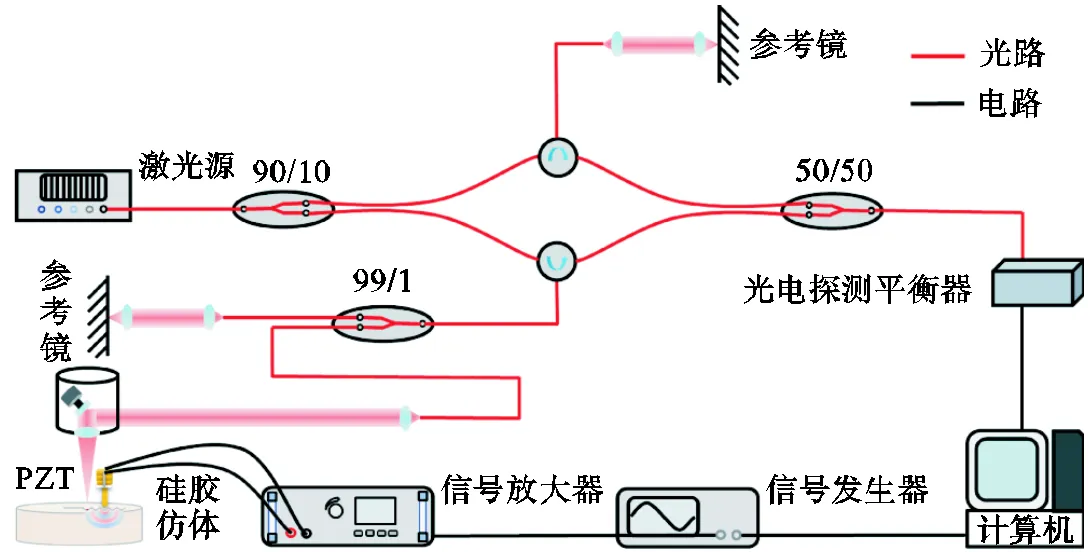
图4 机械激励弹性波OCE系统结构示意

OCE系统获取的是激励产生的相位信号．当试样受到外部激励发生变形时，采样点在一个完整时间序列内会产生沿纵向的位移，而OCE系统可获得随时间变化的相位差Δ，两者的关系[16]为

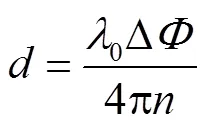
式中：0为光源的中心波长；为被测生物仿体的折射率．

2.2 生物仿体制作及探头类型

将液态硅胶A与液态硅胶B按质量比1∶1的比例混合，加入0.4%的TiO2颗粒(20nm，麦克林)作为散射剂，充分搅拌均匀后倒入到不同的仿体模具中，经过真空处理排出仿体内气泡之后固化制成不同厚度的生物组织单层仿体，如图5(a)所示．在实际情况中，生物组织往往是以层状结构分布的，因此制作了结构不同的单层和双层仿体，具体参数如表2所示．同时准备了不同尺寸与形状的激励探头，分别为球探头与平探头．球探头的直径分别为3.0mm、2.0mm、1.5mm，而平探头的直径分别为2.0mm、1.5mm，具体实物图如图5(b)所示．

图5 仿体与探头的实物图

表2 生物仿体具体参数

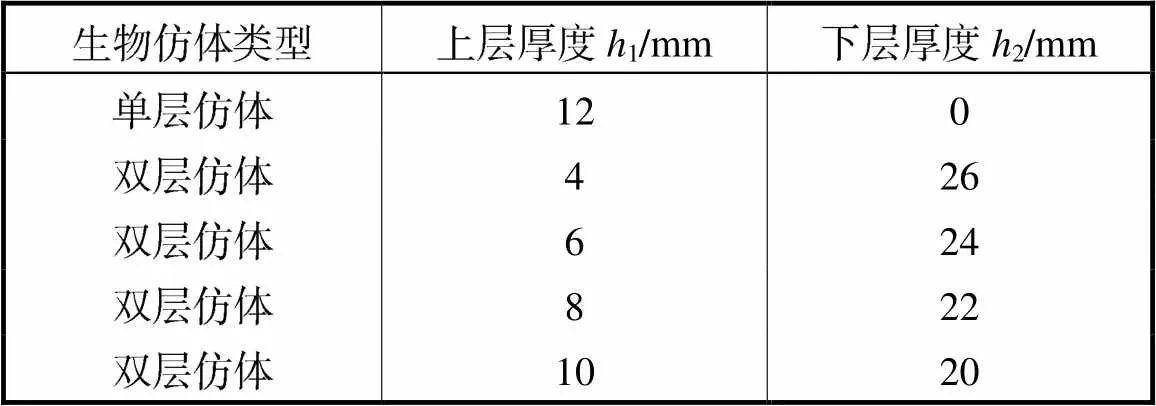
Tab.2 Specific parameters of biological phantom

2.3 实验设置及测量过程

实验共分为3个部分．第1部分采用不同的探头激励仿体，探究探头的尺寸及形状对弹性模量定量测量的影响，基于该实验确定合适的探头．第2部分利用合适的探头作为激励探头，探究基于瑞利-兰姆方程的反演模型在测量单层仿体时的适用性与准确度．第3部分同样采用合适的探头作为激励探头，探究基于瑞利-兰姆方程的反演模型在测量双层仿体时的适用性与准确度．实验示意如图6所示，仿体的密度为1160kg/m3，泊松比＝0.48．为实现OCT采集与探头振动的同步触发，首先利用信号发生器产生1000Hz的触发信号，再经放大器将电压放大至20V加载到压电堆栈上．其中，信号发生器的触发通过OCE系统采集卡工作时的上升沿信号进行控制．在仿体表面点处，调节OCE系统的聚焦镜使光源聚焦到仿体的表面上；在仿体表面的、两点，利用探头分两次进行激励，记录两次激励相位差的变化，根据OCE相移分析法对第一个波谷对应的时间作差，可计算获得时间差Δ，由于、两点的距离是确定的，记为Δ，则弹性波在仿体表面传播的速度由式(12)计算获得．

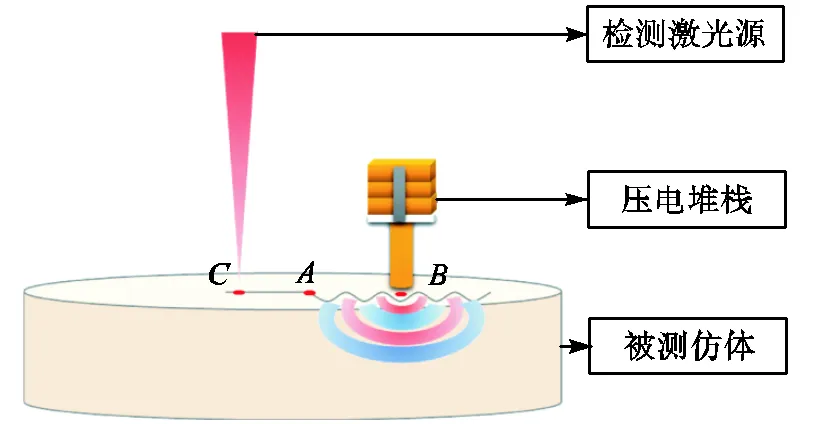
图6 弹性波OCE实验示意

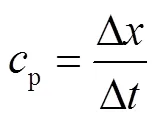
对于OCE获取到的数据进行傅里叶变换，可获得样品表面的相位随时间的变化，图7为利用OCE系统采集的3mm厚仿体表面的相位差信息以及滤波结果．为准确计算波速，采用零相移的低通滤波器对信号进行数据处理．零相移滤波的处理原理是对原始信号先完成一个方向的滤波，然后将滤波后的序列逆序，再利用同一个滤波器做反向滤波，滤波得到的序列最后再逆序，便能得到滤波结果[17].经过处理的数据，既能消除高频噪声，又能保留准确的波谷对应时间．

在获得波速后，利用上述的测量方法可绘制得到不同频率下的波速曲线，即频散曲线．根据频散曲线确定稳定点位置，将该位置对应的波速代入式(10)即可得到被测组织的弹性模量，具体流程如图8所示．

2.4 仿体弹性模量测试

采用单轴拉伸实验测量仿体的弹性模量，从仿体中切下一块13.15mm×5.50mm×3.00mm的试样，并将仿体试件两端固定夹紧在拉伸实验机上，如图9(a)所示，在拉伸速率为0.01mm/s的条件下进行拉伸，获取材料的应力-应变曲线．应力-应变曲线如图9(b)所示，可以发现该仿体在承受35MPa以内的拉应力载荷时，应力-应变曲线具有很好的线性．根据这一特点，可将仿体假设为线弹性介质，并通过曲线拟合得到仿体的弹性模量为477.462kPa．同理可获得双层仿体的上层介质的弹性模量为112kPa．

图8 实验方法流程

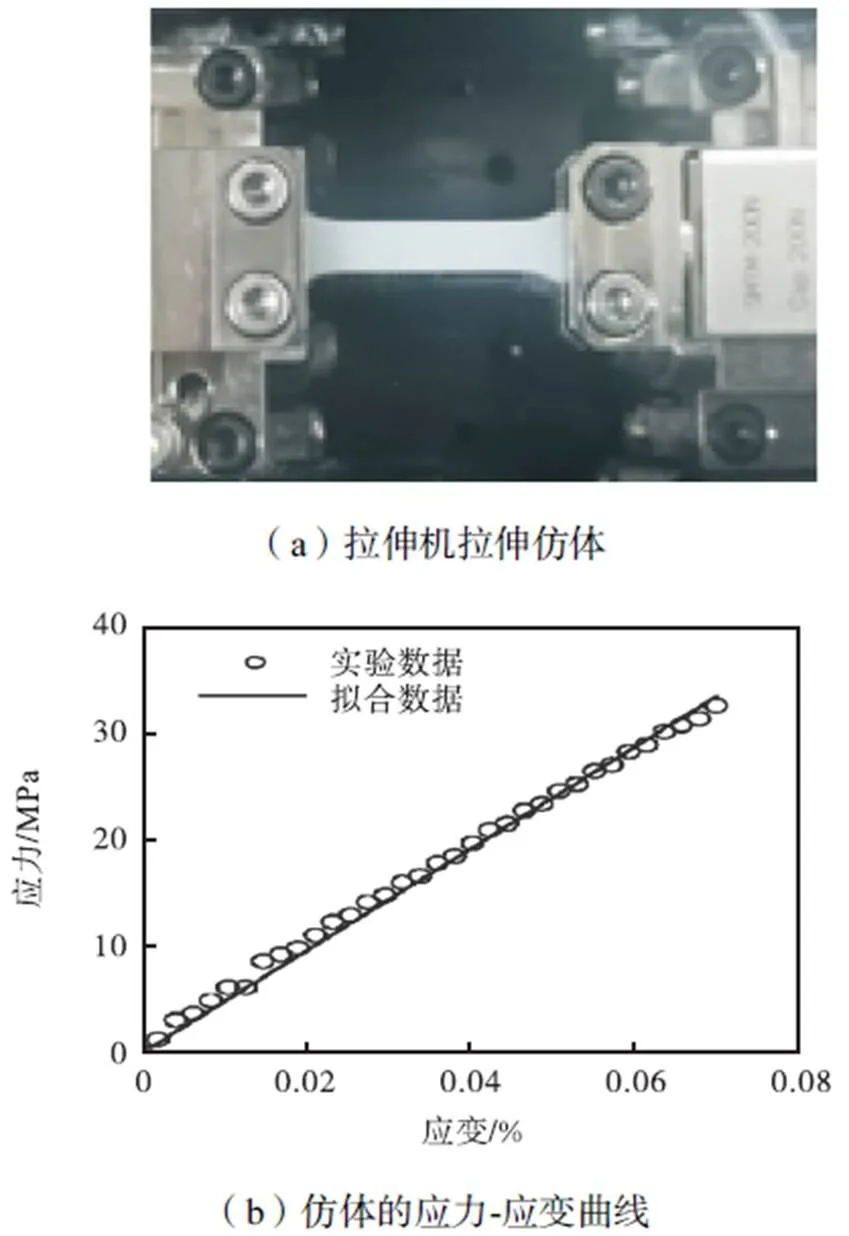
图9 仿体的拉伸实验及应力-应变曲线

3 实验结果

3.1 探头类型对测量波速的影响

图10为采用不同类型探头的实验结果．为了保证实验结果的可靠性，在1000Hz连续激励信号的条件下，通过不同类型探头对厚度为12.16mm的硅胶仿体进行多次实验测试，并将计算得到的波速代入式(10)，获得不同类型探头激励下的弹性模量．从图10可以观察到，随着探头直径的增大，计算弹性模量数值增大，其中，2.0mm球探头以及1.5mm平探头与拉伸实验得到的弹性模量相差较小，误差分别为2.41%和2.66%；比较计算弹性模量的方差带，1.5mm平探头和2.0mm球探头的方差分别为58.639kPa和49.996kPa，因此在球形探头激励的条件下，实验测量的弹性模量更加稳定．实验结果表明，2.0mm球探头作为激励探头对测量波速的影响 最小．

图10　　采用不同类型探头激励时原位测量的弹性模量与拉伸实验测量的弹性模量数值对比

3.2 单层仿体测量结果

采用第1.1节提出的模型，对于给定厚度的生物组织仿体，可以根据模型给定的频厚积确定激励频率．对12mm厚度的硅胶仿体分别施加频率为400Hz、600Hz、800Hz、1000Hz、1200Hz、1400Hz、1600Hz的机械激励，根据OCE相位分析方法，可以测量获得波速，并代入式(10)中得到弹性模量，图11是不同激励频率下原位测量的弹性模量与拉伸实验测量的弹性模量的相对误差，其中由模型确定的激励频率为1000Hz时相对误差最小，最小值为2.68%．

图11　　原位测量的弹性模量与拉伸实验测量的弹性模量的相对误差

3.3 双层仿体测量结果

采用频率为100～3000Hz、步进为100Hz的正弦激励加载，获得如图12所示的频散曲线．根据模型确定的频厚积＝12kHz·mm，可获得不同厚度对应的激励频率，分别为3000Hz、2000Hz、1500Hz、1200Hz．图12中黑色虚线表示的是根据拉伸实验获得的对比组弹性模量，折线表示的是不同激励频率下原位测量获得的弹性模量．从图12中可以发现在对应的激励频率下，不同厚度仿体测量得到的弹性模量与对比组弹性模量接近，误差均在3%以内．

图12 双层仿体的频散曲线

3.4 猪皮测量结果

为了验证该方法测量生物组织的有效性与准确性，对猪皮组织进行测试，如图13(a)所示．通过拉伸实验(见13(b))测量获得被测区域组织的平均弹性模量为2.908MPa．利用OCE技术可获得相位差的变化信息(见图13(c))以及所测波速与频率的关系曲线(见图13(d))，取曲线的拐点处的波速p＝54m/s即平稳值，通过排水法测得猪皮组织的平均密度为＝1241kg/m3，泊松比＝0.48代入式(10)可得弹性模量＝2.948MPa，相对误差为1.38%．

图13 猪皮测量结果

4 结 语

本研究提出了一种基于瑞利-兰姆方程原位测量软材料弹性模量的OCE方法，通过优化机械激励探头形状和尺寸的选择，降低了其对弹性波波速的影响，提高了测量结果的精度．在上述结果基础上，根据瑞利-兰姆方程的数值解，在确定仿体厚度的情况下，匹配合适的激励频率获得弹性模量，单层生物仿体的测量误差在3%以内．在匹配的激励频率下，双层仿体测量结果与拉伸结果几乎一致，证明了该方法在测量上层仿体时不受下层仿体的影响．最后，利用该方法对猪皮进行测量，测量结果与拉伸实验结果的相对误差为1.38%．该方法进一步拓展了机械激励弹性波OCE方法对生物组织的适用范围，为准确地获取生物组织的弹性模量信息提供了一种有效的手段.

［1］ Gennisson J L，Baldeweck T，Tanter M，et al. As-sessment of elastic parameters of human skin using dy-namic elastography[J]. IEEE Transactions on Ultrasonics Ferroelectrics & Frequency Control，2004，51(8)：980-989.

［2］ 卢天健，徐 峰. 皮肤的力学性能概述[J]. 力学进展，2008，38(4)：393-426.

Lu Tianjian，Xu Feng. Mechanical properties of skin：A review[J]. Advances in Mechanics，2008，38(4)：393-426(in Chinese).

［3］ Kennedy B F，Kennedy K M，Sampson D D. A review of optical coherence elastography：Fundamentals，techniques and prospects[J]. IEEE Journal of Selected Topics in Quantum Electronics，2014，20(2)：272-288.

［4］ Liang X，Orescanin M，Toohey K S，et al. Acousto-motive optical coherence elastography for measuring material mechanical properties[J]. Optics Letters，2009，34(19)：2894-2896.

［5］ Chin L，Curatolo A，Kennedy B F，et al. Analysis of image formation in optical coherence elastography using a multiphysics approach[J]. Biomedical Optics Ex-press，2014，5(9)：2913-2930.

［6］ Song S，Huang Z，Nguyen T M，et al. Shear modulus imaging by direct visualization of propagating shear waves with phase-sensitive optical coherence tomogram-phy[J]. Journal of Biomedical Optics，2013，18(12)：121509-1-121509-7.

［7］ Shang W，Larin K V. Shear wave imaging optical coher-ence tomography(SWI-OCT) for ocular tissue biome-chanics[J]. Optics Letters，2014，39(1)：41-44.

［8］ Li C，Guan G，F Zhang，et al. Laser induced surface acoustic wave combined with phase sensitive optical co-herence tomography for superficial tissue characteriza-tion：A solution for practical application[J]. Biomedical Optics Express，2014，5(5)：1403-1418.

［9］ 张小艺，孙翠茹，吕旭峰，等. 基于压电双脉冲剪切波加载和光学相干断层扫描的生物组织弹性测试技术[J]. 实验力学，2019，34(1)：12-22.

Zhang Xiaoyi，Sun Cuiru，Lü Xufeng，et al. On the biological tissue elasticity measurement technique based on piezoelectric double-pulse shear wave loading and op-tical coherence tomography[J]. Journal of Experimental Mechanics，2019，34(1)：12-22(in Chinese).

［10］ Kirby M A，Pelivanov I，Song S，et al. Optical coher-ence elastography in ophthalmology[J]. Journal of Bio-medical Optics，2017，22(12)：121720-1-121720-28.

［11］ 郑佳星，王丹凤，陈金龙，等. 基于瑞利波光学相干断层扫描的非均质生物组织弹性测试技术[J]. 实验力学，2020，35(1)：33-40.

Zheng Jiaxing，Wang Danfeng，Chen Jinlong，et al. Heterogeneous biological tissues elastic measurement based on Rayleigh wave optical coherence tomography [J]. Journal of Experimental Mechanics，2020，35(1)：33-40(in Chinese).

［12］ Li C，Guan G，Huang Z，et al. Full skin quantitative optical coherence elastography achieved by combining vibration and surface acoustic wave methods[C]//Dy-namics & Fluctuations in Biomedical Photonics Ⅻ. San Francisco，USA，2015：93220O-1-93220O-9.

［13］ Viktorov I A. Rayleigh and Lamb Wave—Physical Theory and Applications[M]. New York：Plenum Press，1967.

［14］ Ramier A，Tavakol B，Yun S H，et al. Measuring me-chanical wave speed，dispersion，and viscoelastic modulus of the cornea using optical coherence elastogra-phy[J]. Optics Express，2019，27(12)：16635-16649.

［15］ Graff K F. Wave Motion in Elastic Solids[M]. New York：Clarendon Press，1975.

［16］ Kennedy B F，Kennedy K M，Sampson D D. Optical coherence elastography[J]. Optics and Photonics News，2015，26(4)：34-39.

［17］ 陈淑珍，杨 涛. 零相移滤波器的改进及实现方法[J]. 武汉大学学报，2001，47(3)：373-376.

Chen Shuzhen，Yang Tao. Improvement and realization of zero-phase filter[J]. Journal of Wuhan University，2001，47(3)：373-376(in Chinese).

Optical Coherence Elastography for the in Situ Measurement of the Elastic Modulus of Soft Materials

Chen Jinlong1, 2，Pan Hang1, 2，Lin Xianglong1, 2，Hu Yongzheng1, 2，Sun Cuiru1, 2，Qiu Wenhao1, 2

(1. School of Mechanical Engineering，Tianjin University，Tianjin 300354，China；2. Tianjin Key Laboratory of Modern Engineering Mechanices，Tianjin 300354，China)

Elastic wave optical coherence elastography is a method that can quantitatively measure the elastic modulus of biological tissues by using wave velocity. It has an important application value in medical research and disease diagnosis. At present，several measurement errors occur in evaluating the elastic modulus of soft materials with a certain thickness using Rayleigh wave theory. To improve the accuracy of elastic modulus measurement，an inverse method of elastic modulus parameters based on the Rayleigh-Lamb equation is proposed. According to the numerical solution of the Rayleigh-Lamb equation，the elastic modulus was obtained by matching the appropriate excitation frequency under the condition that the thickness of the phantom was determined. The elastic modulus measured in situ was compared with the tensile experiment results，and the relative error was found to be within 3%. It is found that the elastic modulus measured in situ is almost the same as that measured by the tensile experiment under the matching excitation frequency，which demonstrates that the method is not affected by the lower layer when measuring the upper layer. The results of real pig-skin tissue measurement show that the method can be applied to skin tissue measurement. In this study，the optical coherence elastic measurement method of soft materials in situ provides a more accurate measurement method for the quantitative characterization of the elasticity of biological tissues.

elastic wave；optical coherent elastography；Rayleigh-Lamb equation；elastic modulus

10.11784/tdxbz202109033

TK448.21

A

0493-2137(2023)02-0111-08

2021-09-24；

2021-11-29.

陈金龙（1966—  ），男，博士，教授，jlchen66@tju.edu.cn.

孙翠茹，carry_sun@tju.edu.cn.

天津市自然科学基金重点资助项目(20JCZDJC00760)；国家自然科学基金资助项目(11972249，12272262)；国家自然科学基金重大资助项目(11890680).

Supported by the Key Natural Science Foundation of Tianjin，China(No. 20JCZDJC00760)，the National Natural Science Foundation of China(No.11972249，No.12272262)，the Major Program of the National Natural Science Foundation of China(No. 11890680).

(责任编辑：王晓燕)