改进萤火虫算法与K-means算法结合的配电网负荷聚类特性分析
2023-02-15王继东顾志成葛磊蛟赵长伟贾东强
王继东,顾志成,葛磊蛟,赵长伟,贾东强
改进萤火虫算法与K-means算法结合的配电网负荷聚类特性分析
王继东1,顾志成1,葛磊蛟1,赵长伟2,贾东强3
(1. 教育部智能电网重点实验室(天津大学),天津 300072;2. 国网天津市电力公司城东供电分公司,天津 300650;3.国网北京市电力公司电力科学研究院,北京 100075)
负荷聚类特性分析是实现配电网的定制电力、高品质供电、高可靠性供电的重要基础.然而现有的K-means聚类分析方法,受限于数据样本集和聚类初始中心的选取等,会出现因初始中心不同造成聚类结果差异大的问题.为此,针对配电网负荷数据特点,提出一种基于改进萤火虫算法和K-means算法结合的配电网负荷聚类特性分析方法.利用萤火虫优化算法全局搜索能力强的优势,考虑类内相似度和类间差异度,寻优K-means算法初始中心,使聚类结果的聚类有效性指标取得最小值;进一步针对萤火虫算法在处理负荷数据时的弱点,通过密度法为萤火虫算法加入优秀初代个体,改进吸引公式以及个体间概率吸引移动的方式优化迭代过程中的个体移动方式,加快萤火虫算法前期收敛速度,并实现后期稳定收敛,算法更快地接近极值,计算速度更快.算例验证了本文所提算法的聚类有效性,并针对某配电台区电力负荷数据,寻得K-means算法最优初始中心,使得聚类结果的戴维森堡丁指标(Davies-Bouldin index,DBI)最小,负荷聚类结果类内差异小,类间差异大,最终聚类中心的特征代表性强,为负荷类型划分、聚类特性分析提供重要依据,为需求侧差异化电力服务定制奠定有力基础.
配电网负荷;K-means聚类;萤火虫算法;数据驱动方法
配电网是电力能源的枢纽,直接面向成千上万的终端用户,居民、商业和工业等不同电力用户混杂,并且不同电力用户供电诉求差异大.通过对配电网历史负荷曲线聚类,实现负荷特性分析,寻找其共有内在特性,挖掘其潜在变化规律,是实现配电网电力用户的定制电力、高品质供电、高可靠性供电等服务的重要技术手段之一[1],还能为制定需求侧响应政策以及高精度负荷预测提供数据支撑[2].然而,配电网用户繁多、网络复杂、数据异构,现有的K-means等算法进行配电网负荷聚类时常受样本集、聚类中心点选取随机等因素影响,导致聚类结果不同,聚类效果差异明显[3].另外,负荷聚类要求兼顾特征性与通用性,少量负荷单独分类会造成结果通用性低,大量负荷扎堆会造成结果特征性差.因此,为确保负荷聚类结果应用于电力营销业务的泛用性和差异性,如何选取初始中心点,给出唯一解并确保配电网负荷聚类效果,值得深入研究.
K-means算法是当前应用最广泛的聚类分析方法之一.该算法原理简单、计算速度快、可行性高,但其聚类数的选取直接影响聚类结果,并且对于初始中心点的选取敏感,会造成聚类结果局部最优、收敛速度慢以及不稳定等问题[4].针对算法初始中心选取问题,常用方法有经验法、择优法、距离法、密度法等,也有衍生的K-means++算法,使距离因素影响初始中心的选择概率.国内外学者们在电力领域的应用上,也进行了一些研究.文献[5]通过K-means聚类分析方法对电力变压器分类,实现了变压器经济运行分析;文献[6]应用 K-means聚类提取风电的时间序列数据特性,用以实现风力发电预测;文献[7]分析了对用户分组时影响K-means聚类效果的因素,提出改进方向;文献[8]针对负荷维度大问题优化K-means算法,提高了聚类效果;另外,还有其他聚类算法如自适应稳健聚类方法[9]、改进AP聚类算法[10]用于电力系统负荷分类,但其聚类方法复杂度较高.
在K-means算法初始中心选取的优化算法方面,一般应用启发式算法针对某一指标选取初始中心确定最优结果,确保同一样本集的聚类结果唯一且聚类效果最好.在众多最优化启发式算法中,遗传算法、差分算法交叉变异过程导致的个体易出界不稳定,并且种群迭代过程调用聚类算法次数多;蚁群算法模拟蚁群路线,搜索范围大速度慢,更适用于配电网规划;萤火虫算法(firefly algorithm,FA)模拟萤火虫的寻偶觅食过程,目标性更强,易于实现且全局搜索能力强[11],更契合K-means算法.
目前有较多改进的萤火虫算法[11-13],重点针对较大范围内无明显参考的初代选取,以及多峰值扩大搜寻范围,跳出局部实现全局搜索,适合于需要大范围搜索的未知问题.在萤火虫算法与K-means结合方面,文献[14]应用精英反向学习策略筛选下一代个体并采用变参数优化,但未优化初代选择,文献[15]为应对复杂优化问题提出邻域吸引,从减少吸引次数角度加快算法效率,文献[16]应用加权法解决样本影响程度不同的问题.
本文针对配电网负荷聚类的样本属性统一、参考性高、搜索范围较小和求解稳定性要求高的特点,就萤火虫算法早期收敛速度慢、后期收敛不稳定、在收敛后又退出收敛状态的问题做出改进,提出一种改进萤火虫算法与K-means算法结合的方法以实现配电网负荷聚类.通过在初代种群中加入优秀个体的方式实现算法加速,采用简化吸引公式以及概率吸引两种方式增加计算效率,采用变参数增强收敛稳定性.本方法可给出配电网负荷聚类最优结果,为配电网负荷聚类特性分析、供电服务定制提供决策依据.
1 配电网负荷聚类分析
配电网有着庞大的负荷数据信息和复杂的负荷变化规律,这使得定制电力服务,满足用户差异化用电需求成为难题,负荷合理划分重要性突显.为此,本文提出一种改进萤火虫算法与K-means算法结合的方法用于配电网负荷聚类分析,配电网负荷聚类应用流程如图1所示.
对于某一配电台区,首先通过监测装置收集长时间的用户电力数据,形成电力用户用电数据库.然后以电力用户用电数据库收集的历史数据为原始数据,从中提取负荷数据并进行处理,作为输入数据.应用K-means聚类算法和优化算法,遍历众多分类结果,找到分类效果最好的聚类结果,并根据结果分析负荷特性规律.最后结合聚类结果与负荷特性,针对不同配电网用户差异化需求,为制定不同类型负荷的配套管理策略提供数据支持,助力定制电力、高品质供电、高可靠性供电服务.
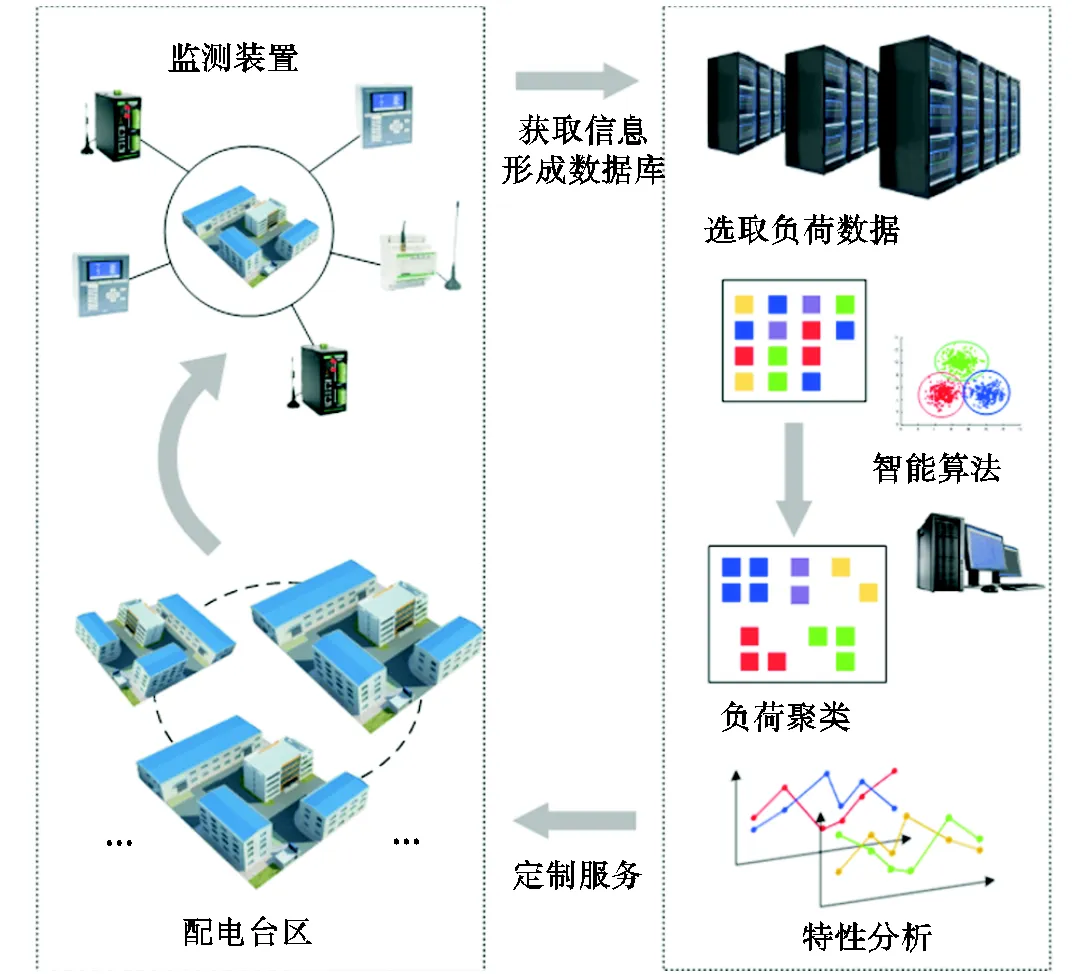
图1 配电网负荷聚类应用流程
2 基于改进萤火虫算法的K-means算法
2.1 K-means聚类算法
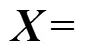
算法的主要流程如下:
步骤1从整个数据集中随机选取个数据点作为初始中心;
步骤3按照簇内平均值计算新的聚类中心点;
步骤4判断前后两次迭代得到的聚类中心点变化量是否小于预定值,是则转步骤5,否则转步骤2;
步骤5输出聚类结果,并对结果做出评价.
传统K-means算法有两个主要缺陷:一是需要预先给定值,不同的值必然带来不同的聚类结果;二是初始中心点对聚类结果影响很大,初始中心的选择可能使结果陷入局部最优,还会影响收敛速度和稳定性.
对于配电网负荷聚类,不同的负荷数据作为初始中心常常会产生不同的分类结果,同一负荷在不同初始中心影响下会被分到不同的组,而聚类数的选择也会影响同组负荷的相似度与定制电力服务的复杂度,因此需要选取合适的聚类个数并且进行聚类寻优,确保同类负荷的类内相似度与不同类负荷的类间差异性最大,实现不同定制服务特征性强、差异性大.
2.2 改进萤火虫算法
2.2.1 萤火虫算法相关概念
萤火虫算法是受萤火虫的发光行为启发而提出的随机优化算法.萤火虫通过发光彼此吸引,发光亮度低的萤火虫在其视野范围内被吸引向亮度高的萤火虫移动,局部范围内亮度最高的萤火虫随机移动,通过萤火虫的发光和移动搜索空间中的所有可行解来寻找最优解,整个群体具有正反馈机制,加快算法收敛,提高获得最优解的概率,并且具有很强鲁棒性,可用于寻找最佳负荷分类结果.其设定主要有如下参数.
1) 吸引度
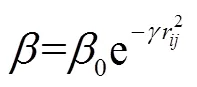
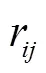
2) 位置更新
萤火虫被吸引向更亮的个体移动,即

萤火虫为最亮时随机移动,即
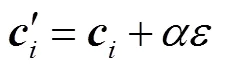
萤火虫优化算法中萤火虫位置代表数据,亮度代表评价指标,首先随机选取数据生成萤火虫初代个体的位置,然后根据当前位置计算某一评价指标作为亮度并记录本代亮度最高的个体,然后根据亮度和距离确定个体间吸引度,使萤火虫按照一定准则移动,位置更新后作为下一代进入循环,循环过程中约束移动范围确保其不出界,直到满足结束条件后,选取记录亮度最高的个体即评价指标最优个体的位置信息作为输出.
2.2.2 算法改进
配电网负荷数据时间维度长、季节性波动大,区域负荷受相同气候因素影响,导致负荷变化趋势相似度较高,可能分类较多,而萤火虫算法存在早期收敛速度慢、后期收敛不稳定的问题,因此需要优化迭代过程,加快前期寻找极值的速度,增强后期收敛稳 定性.
1) 初代个体选择
萤火虫的初代个体是通过随机法产生:随机选择个输入数据作为一组初始中心,并将其作为一个个体的位置,重复该过程直到生成所有个体.由于萤火虫的移动依赖更亮的萤火虫吸引,这就需要有更亮的优秀个体引导,因此优秀个体对算法结果有很大影响.针对配电网负荷,各类型负荷变化规律差异较大,同类型负荷变化规律相近且数量较多,可以应用密度法获取多个负荷作为典型参考.本文应用密度法计算一组初始中心,将其作为一个优秀个体加入种群中.
密度法从数据集中选择个处于高密度区且相互距离较远的点作为初始中心,符合现实中同类型负荷有时间规律的特点,流程如下.


步骤2计算数据点之间的平均距离为
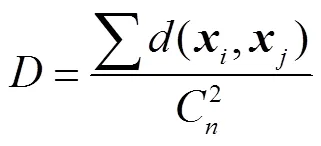
步骤3对于每一个数据点,寻找以该点为中心距离范围内包含的数据点的个数,即密度值,其表达式为
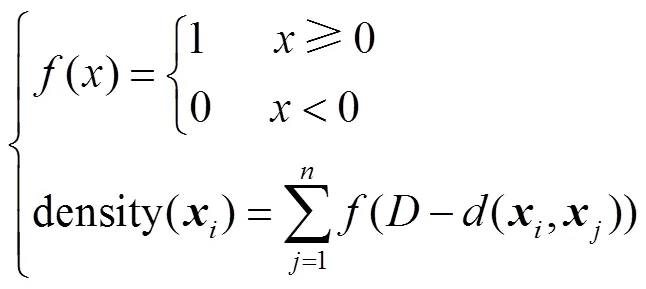

步骤5判断是否已找到个初始中心,是则转步骤7,否则转步骤6;
步骤6将步骤4中确定的初始中心和与其距离为范围内包含的数据点删除,然后转至步骤4;
步骤7输出初始中心.
通过以上步骤获取一组个初始中心,其代表一个优秀个体的位置信息,通过初代种群中加入优秀个体,使算法能够更快接近极值点.但当值取值较大时,无法获取足量的点形成一个个体,此时将步骤2计算得到的缩小适当倍数再用于步骤3的计算,直至可以获取足够的点形成一个个体.
2) 位置更新
在传统萤火虫算法中,个体位置更新公式中的扰动项加大了算法搜索范围,使得算法在迭代的初始阶段在全局范围内搜索最优值,避免过早地陷入局部最优解,增加算法的局部寻优能力,但在最后搜索阶段会因为扰动过大,使个体移动距离过大,造成个体无法到达最优位置,在极值点附近反复振荡,导致算法整体收敛速度较慢,稳定性比较差.因此对进行修改,使值随迭代次数的增加而减小,但不会降为0失去扰动作用.

配电网负荷数据往往时间长维度多,导致在个体位置更新公式中使用指数运算的运算速度慢,迭代时间长,因此利用等价无穷小原理对吸引度公式进行替换,以减小计算量,加快运算速度.
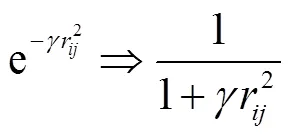
式(9)满足随增大而减小的要求,且在=0处,即发光处该值为1,无衰减,在=∞处(表现为本代中该个体亮度最高)两式等价无穷小,被吸引移动变为随机移动.
经过修改后的个体位置更新公式为
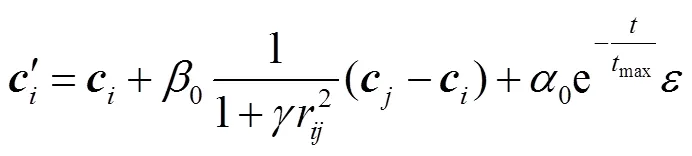
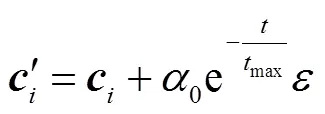
式(10)表示萤火虫被吸引向移动,式(11)表示萤火虫随机移动.
在进行位置更新时,萤火虫会被亮度更高的个体依次吸引,向不同的方向多次移动,容易造成振荡.针对此问题,首先搜索所有亮度更高的个体,再依亮度大小排序,确定向移动的概率,向亮度差异越大的个体移动的概率越大,而对于亮度略高于的个体则可能不被吸引,以此减少移动次数.
个体向移动的概率为
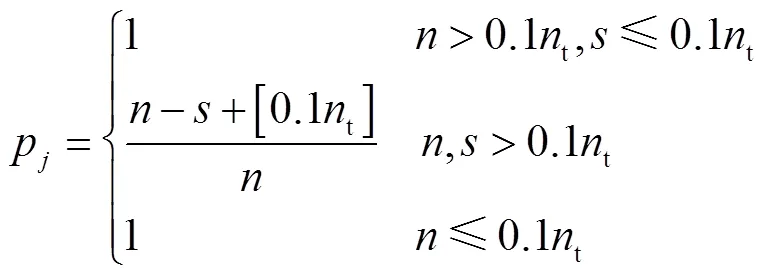
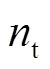
2.3 算法应用
K-means算法用于聚类分析,萤火虫算法用于K-means参数寻优,将萤火虫算法与K-means算法相结合,可实现配电网负荷聚类结果最优.将单个负荷数据作为一个数据点组成输入数据集,将K-means算法初始中心作为萤火虫算法的萤火虫个体,将K-means算法聚类结果作为萤火虫个体发光亮度,通过萤火虫个体的发光、吸引、移动,实现初始中心的变化和寻优,达到负荷类内差异小、类间差异大的目的.萤火虫算法与K-means算法结合后的主要流程如图2所示,应用于电力负荷聚类分析的步骤如下.
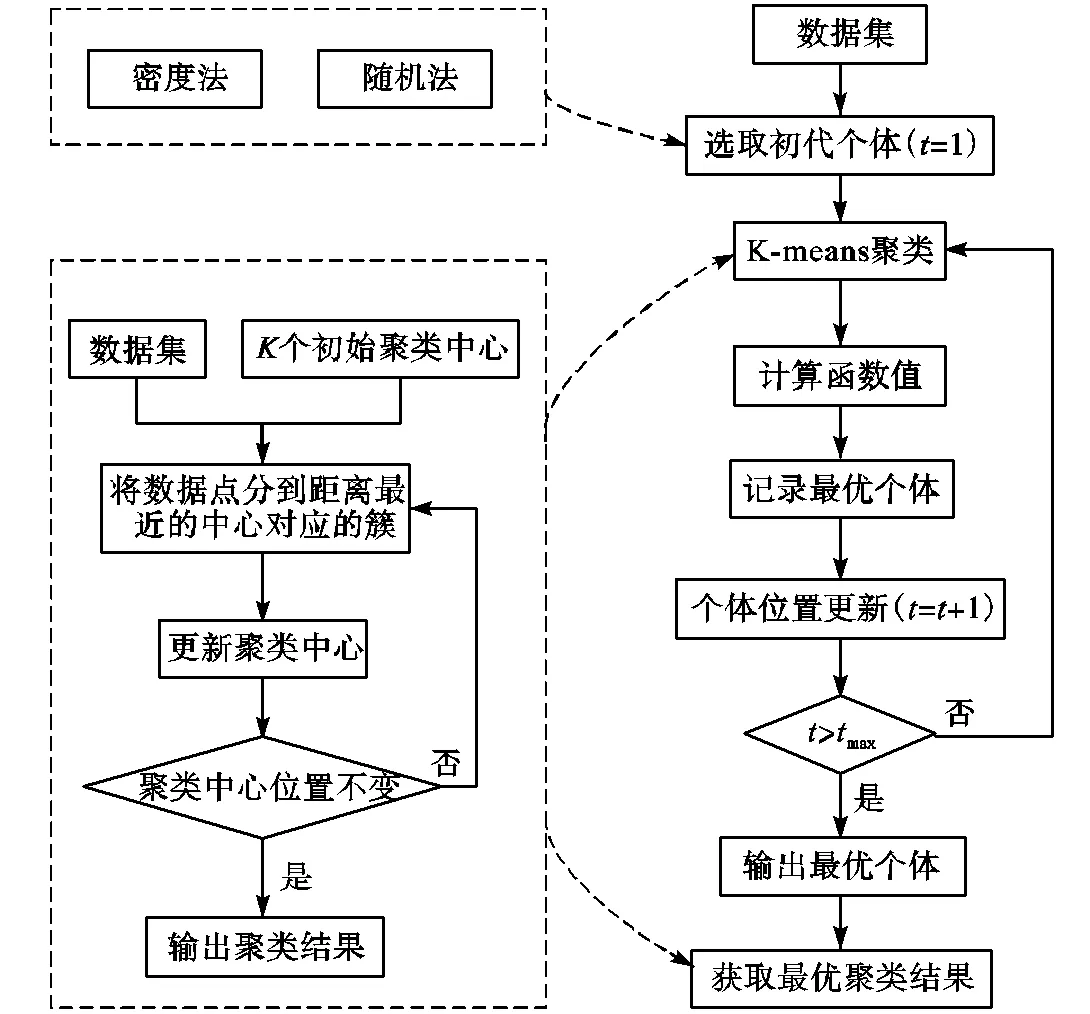
图2 算法主要流程
步骤1假设配电网电力负荷数据包含个电力负荷的个时间段数据.针对负荷采用时间维度的特点,对数据标幺化处理,作为输入数据集.
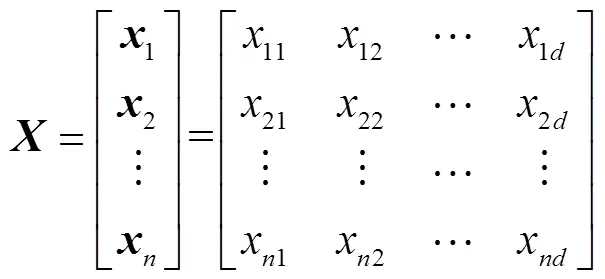

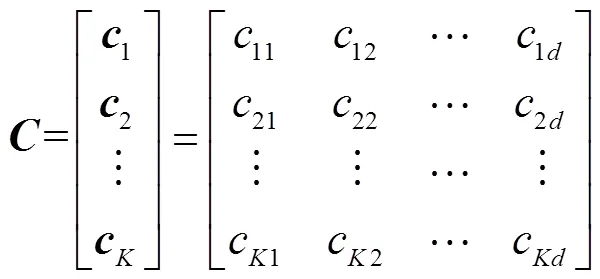
反复随机选取直至取得足够数量(种群预设个体数-1)的萤火虫个体,与通过密度法获取的一个优秀个体组成初代萤火虫种群.
步骤3将数据集和萤火虫个体输入到K-means算法,获取聚类结果,计算体现类内、类间距离的综合性聚类有效性指标戴维森堡丁指标(Davies-Bouldin index,DBI).
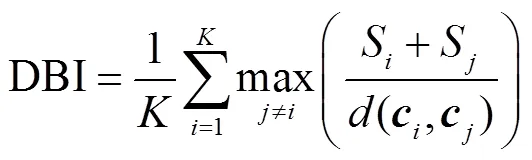

在种群迭代过程中可能会出现多个最亮的个体,即它们的DBI均为最小值,这时需要比较其在K-means聚类过程中的迭代次数,将最小迭代次数的个体作为最优个体.
步骤4获取种群亮度后,记录最亮个体,然后按照式(12)概率吸引移动,用式(10)和式(11)更新个体位置,实现种群迭代.
步骤5判断是否达到最大迭代次数,是则转至步骤6,否则转至步骤3.
步骤6将记录的最亮个体作为最优初始中心,输入到K-means算法获取最优聚类结果,实现配电网电力负荷分类.
3 案例分析
3.1 算法验证
为验证提出算法的有效性,在MATLAB 2018a平台对其进行测试.测试平台搭建环境为 Windows 10 操作系统,Core i7-6700K CPU,8GB运行内存.选取UCI Machine Learning Repository中的3个数据集Ecoli、Glass和Wine检验算法聚类准确性.其中Ecoli数据集删除个数极少的3类.原始数据集经最大最小标准化处理后进行聚类,获取结果后计算总的分类准确率,20次聚类的准确率统计结果如表1所示.可以看出改进后的算法能够更为稳定地给出聚类结果,且准确率相对更高.
表1 聚类准确率

Tab.1 Clustering accuracy
以文献[17]中的数据为基础进一步验证本文所提算法.基于文献案例分析结果选用聚类数为5,采用文献中基于密度法算法与本文算法进行对比,二者聚类结果相同,1~5类负荷数量记为[8,5,8,6,4].
在原有数据基础上每条数据增加少量扰动生成等量数据,将其与原数据组合成新数据集,再次进行对比分析.本文算法聚类结果如图3(a)所示,DBI值为0.8397,1~5类负荷数量记为[16,10,16,12,8],是原数据各类的2倍,结果与新数据生成原理对应.文献[17]中基于密度法的聚类结果如图3(b)所示,DBI值为0.9989,明显大于寻优结果,1~5类负荷数量记为[11,3,28,12,8].
两算法聚类结果关系如图4所示,结合图3可以看出,在增加新数据后,密度法受特殊点影响大,将其单独分为一类,即图3(b)中的第1类,仅有3个,并且与第2类的变化规律差异不大,而图3(a)中的第2类呈现下降规律,第3类呈现上升规律,在图3(b)中却被合为一类,数量近半,但整体趋势差异明显,相似度不高,共有特征不明显.可见,加入扰动增加的新数据对密度法的影响很大,使得聚类效果不稳定,而采用本文算法寻优可以确保聚类效果.
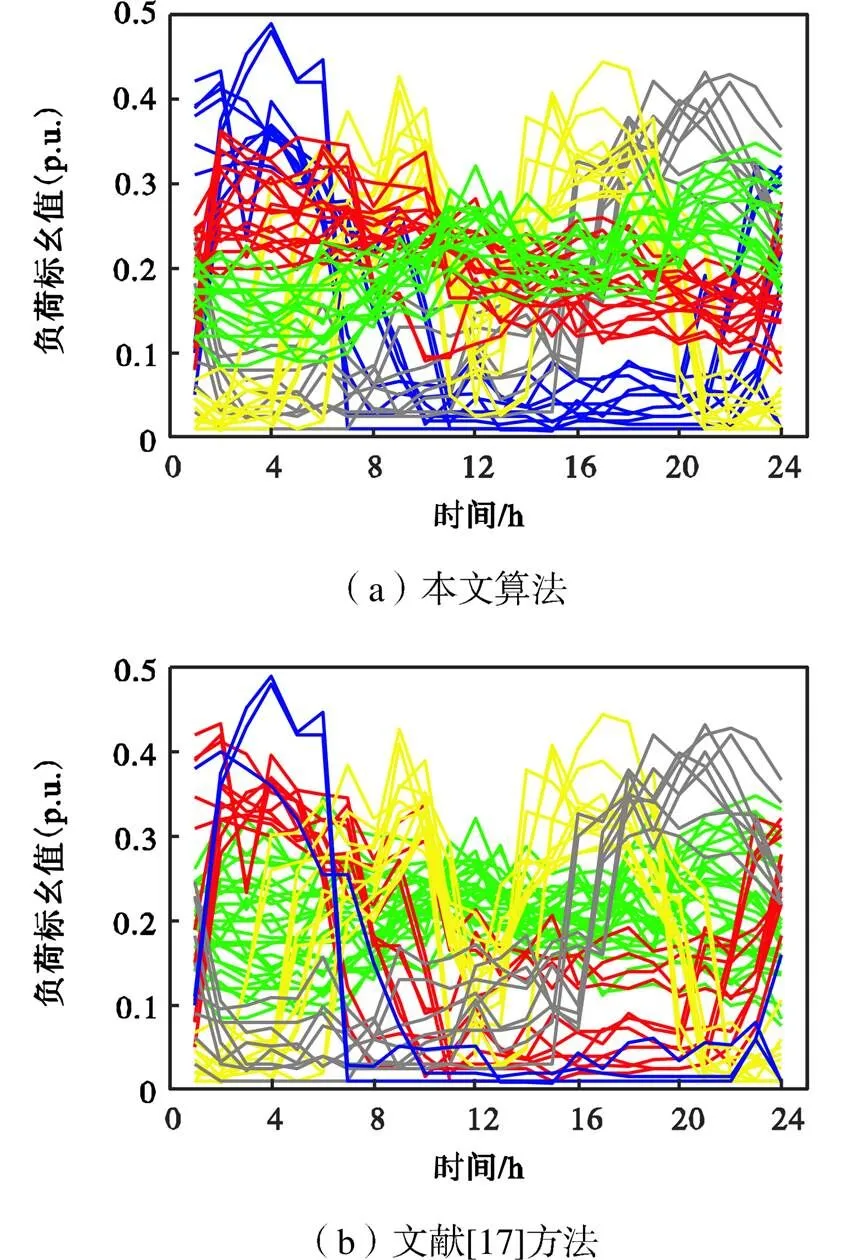

图4 聚类结果关系
3.2 负荷聚类
3.2.1 参数选取
选取天津市某配电台区电力负荷数据作为研究对象.该数据包含97条电力负荷记录,每条记录包含一年内的日平均负荷值,总计365个数据点构成年负荷曲线.
针对数据变化范围[0,0.6],通过调试,选取算法参数0=0.1、0=1、=0.15,此时每次迭代移动距离较为合理.根据负荷数,选取种群个体数30,最大迭代次数20.选取值时,首先确定合理范围,最大值选择在样本数的开方值附近,本例选取范围[3,12]内的整数值作为合理的值进行分类分析.不同值下多次运行程序,确保获取各个值对应最小DBI指标,见表2.当值较大时,密度法获取的初始中心个数小于,此时适当地成倍缩小距离,使其可以取得个初始中心,确保萤火虫算法可以获得一个优秀个体.
然后选取DBI指标较小的值,由图5(a)DBI指标曲线可看出,值取5时,DBI最小,值取8时,DBI次之.使用类内误差平方和(sum of squares for error,SSE)指标进行辅助分析,如图5(b)所示.由于SSE只针对类内,随着值的增大而减小,因此寻找其斜率变化量较大处,可见值取5或6时符合要求.综合两个指标,选取5为最佳聚类数.
表2 不同值下的聚类指标

Tab.2 Cluster indexes under different K values
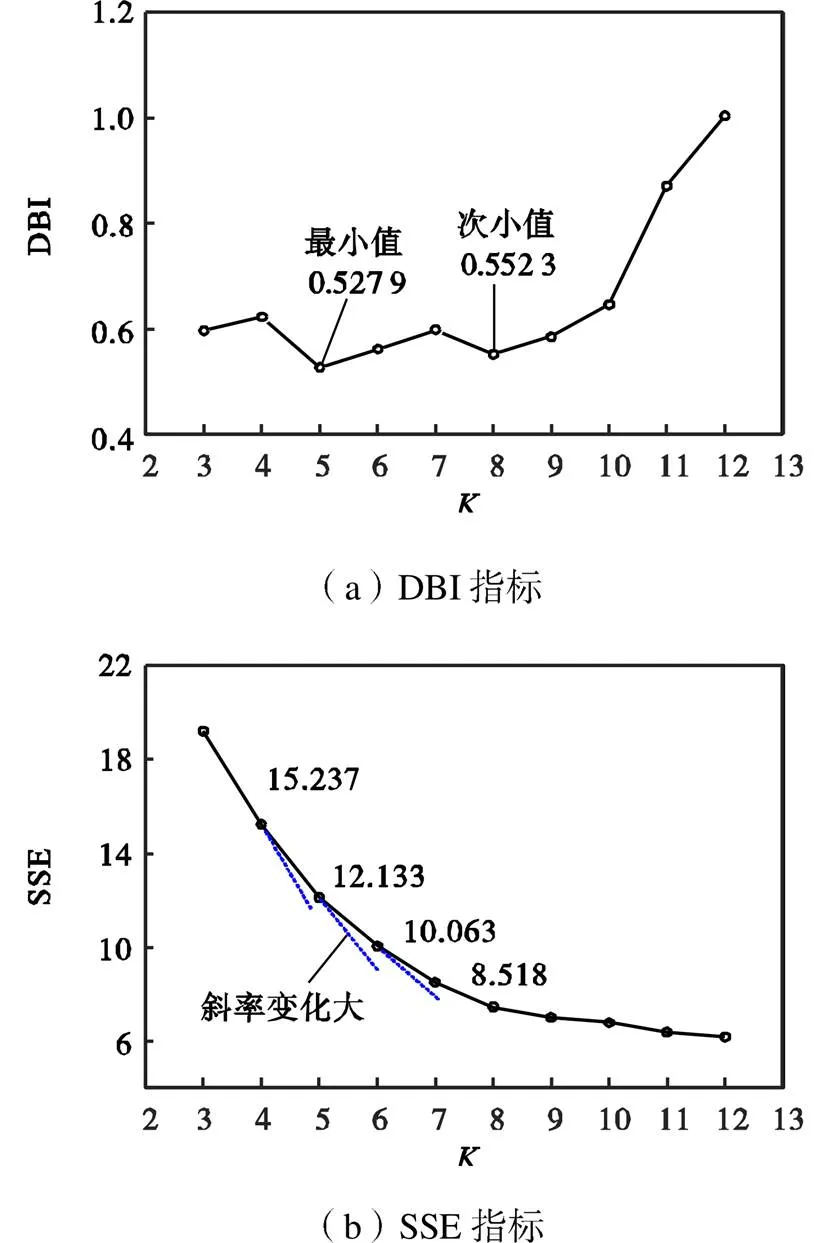
图5 聚类指标变化曲线

3.2.2 聚类结果分析
聚类结果如图6所示,通过聚类分析97个电力负荷被分为5类,如图7所示,各类初始中心与最终聚类中心如图8所示,聚类结果的负荷特征如表3所示,可得出以下结论.
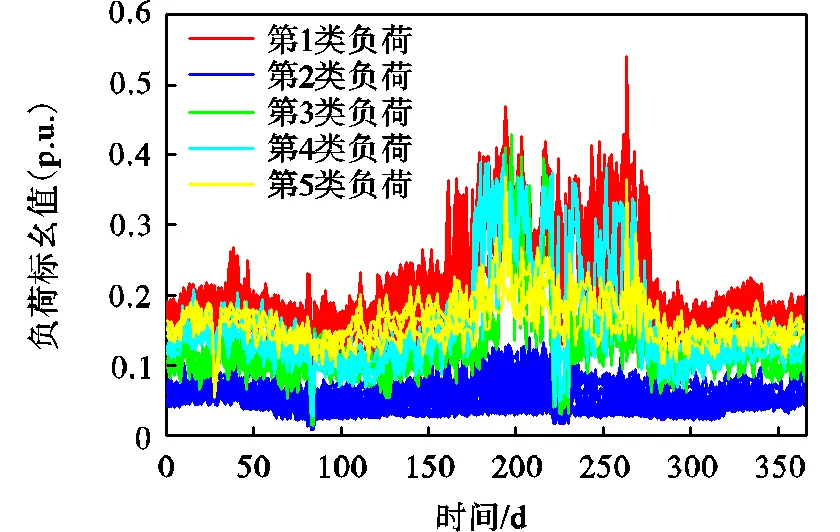
图6 区域电力负荷聚类结果
(1) 第1类负荷均值最大,高峰期持续时间长,在总样本中占比最大,具体表现为:6月中旬至9月末受气温影响为高负荷期,负荷大,持续时间长,8 月中旬降温降雨对其影响较小,1月末出现冬季小高峰,其余月份负荷水平相对较低.
(2) 第2类负荷均值最小,全年变化量小,无明显峰谷期,负荷稳定,但受天气影响3月末与8月中旬出现低值.
(3) 第3类负荷均值较小,高峰期持续时间较长,具体表现为:7月中旬至8月中旬为高负荷期,负荷较大但持续时间短,8月中旬受降温降雨影响大,出现短时低谷,后续恢复至平均水平.
(4) 第4类负荷均值居中,高峰期持续时间短,具体表现为:7月初至9月末为高负荷期,负荷较大,持续时间较长,8月中旬受降温降雨影响大,出现短期低谷,但后续恢复至高值,与第3类有明显区别.
(5) 第5类负荷均值较大,高峰期不明显,在总样本中占比最小,具体表现为:7月初至9月末为高负荷期,持续时间长,8月中旬降温降雨对其影响较小.与第1类负荷的区别是其负荷均值和峰值小,全年变化量相对较小.
通过算法聚类分析,区域负荷被分为5类,根据各类型特征规律,再结合不同配电网用户用电需求,可以实现不同类型负荷的配套管理策略制定,实现峰谷期差异化管理.
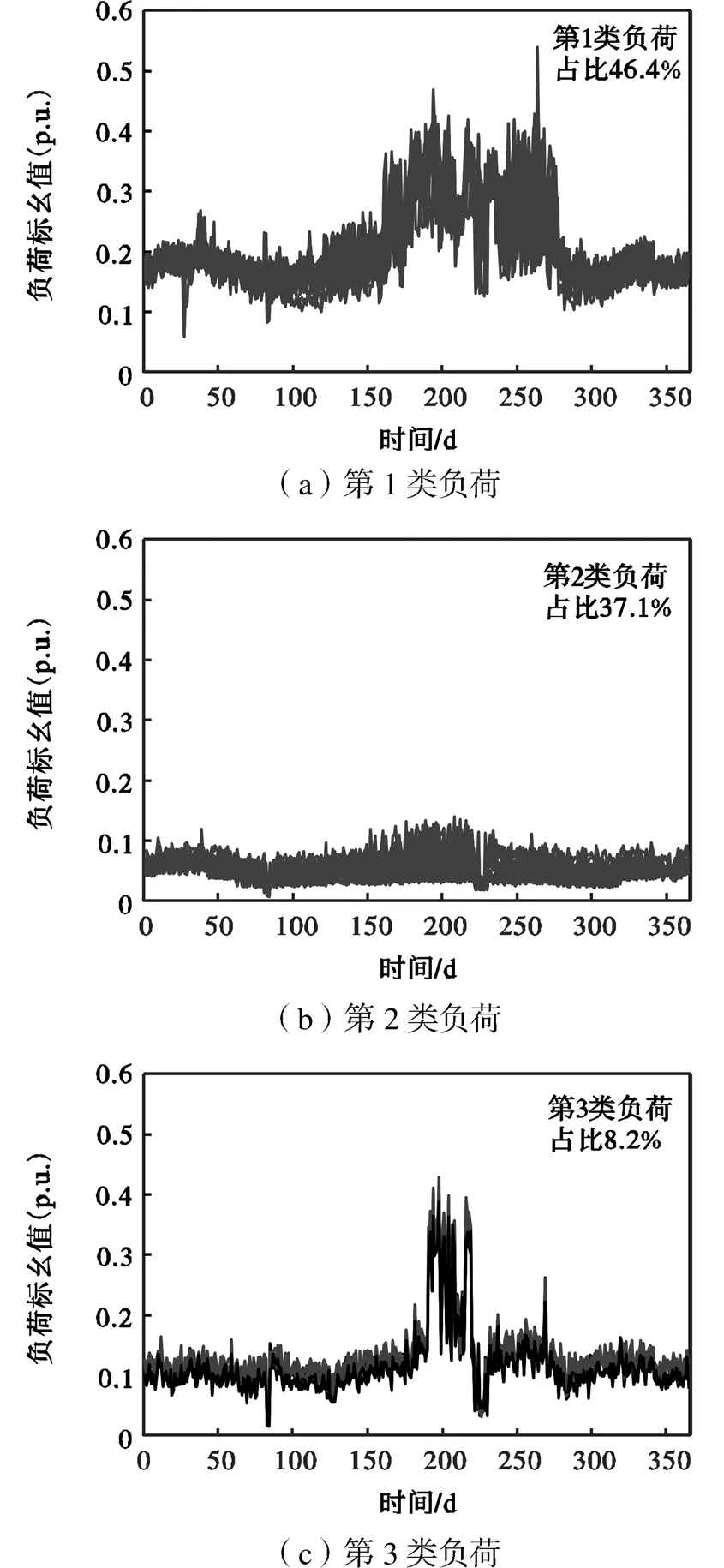

表3 聚类结果的负荷特征

Tab.3 Load characteristics of the clustering results
3.2.3 对比分析
针对=5的情况,分别使用密度法优化K-means算法、K-means++算法和本文算法,聚类结果指标对比如表4所示.由于本文算法对DBI指标进行寻优,该指标取得了最小值,而SSE未涉及类间差异的概念,因此未取得最小值.从类内平均距离1和类间平均距离2来看,密度法的聚类效果更好,但密度法易受孤立点影响,将其单独分为一类,使得平均概念的类内、类间指标数值表现更好,但实际情况并不理想.而DBI指标涉及最大概念,从而减小了此种情况的影响,因此采用该指标进行寻优,获取最佳聚类效果.
表4 聚类结果指标对比
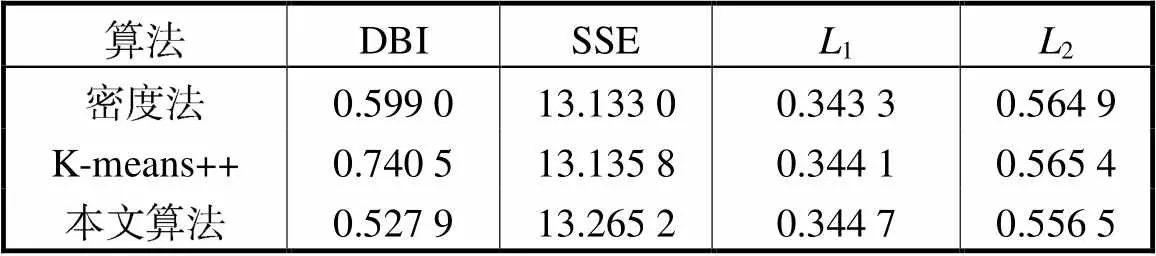
Tab.4 Comparisonof the clustering indexes
分别使用本文改进算法、K-means结合细菌觅食优化(bacterial foraging optimization,BFO)算法[18]、传统的FA算法和精英反向学习(elite opposition based learning,EOBL)萤火虫算法优化的K-means算法[14]进行比较,初代种群基于同一个种群按各算法要求处理,为展示效果将迭代次数设为30,收敛曲线如图9所示.可以看出通过密度法加入的优秀个体能使算法更快取得极值.本文改进算法、FA算法、EOBL-FA算法的迭代后期每代最小DBI值如图10所示,可以看出减小取值使得算法后期在小范围内局部搜索,比采用常值的稳定性更强,而与EOBL-FA算法不同,本文在后期减小但未到零,避免过早失去扰动作用.

图9 算法收敛曲线
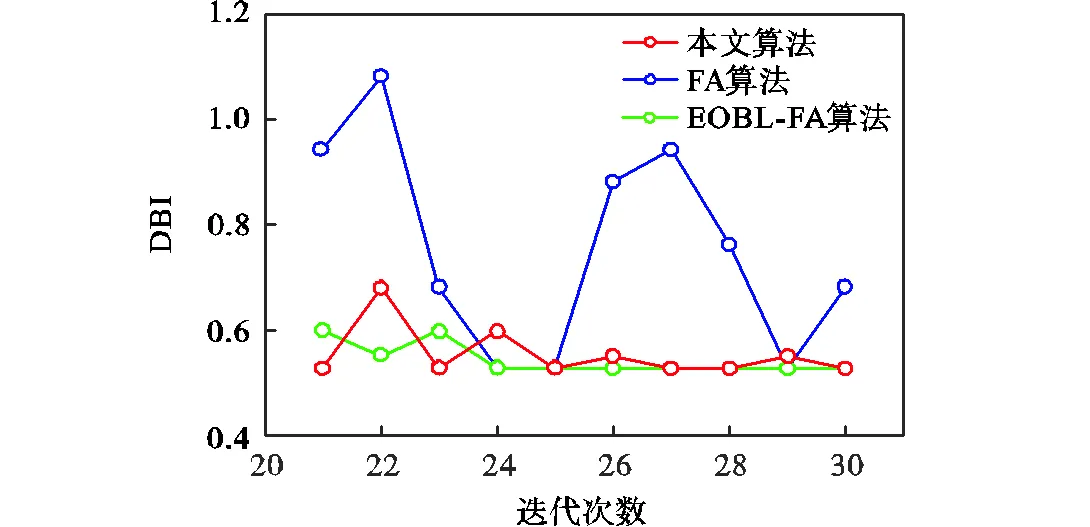
图10 算法后期每代最小值
与其他萤火虫算法比较,各算法运行30次获取平均运行时间如表5所示.本文算法下程序平均用时最短,相比于传统萤火虫算法,本文算法通过降低公式复杂度明显加快了运算速度,降幅约为20.2%,而EOBL-FA算法采取筛选策略会增加用时.
表5 算法用时对比
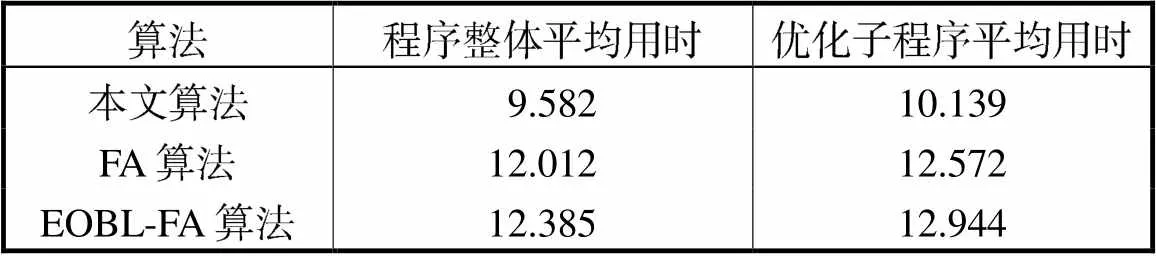
Tab.5 Time-based comparison between the improved and traditional algorithms s
4 结 论
为实现配电网负荷聚类,获取配电台区各类负荷典型特性,本文针对负荷数据特点和算法缺点,提出了一种改进萤火虫算法与K-means算法结合的方法.经案例验证,得出以下结论.
(1) 该算法通过寻优初始中心,获取最优负荷分类结果,实现了负荷聚类以及特性分析.
(2) 在萤火虫算法的初代种群中加入优秀个体,实现了更快接近极值的目的.
(3) 采用简化吸引公式以及概率吸引两种方式实现了算法效率的增加,采用变参数增强收敛稳定性,又避免了过早参数失效.
(4) 在负荷聚类的基础上,后续可进一步针对各类型负荷特性和用户需求研究控制策略,实现需求侧差异化配套电力服务定制.
[1] 葛磊蛟,王守相,张 明,等. 智能用电条件下用户用能管理与服务平台[J]. 电力自动化设备,2015,35(3):152-156.
Ge Leijiao,Wang Shouxiang,Zhang Ming,et al. Power usage management&service platform in smart electricity utilization condition[J]. Electric Power Automation Equipment,2015,35(3):152-156 (in Chinese).
[2] 苏 适,李康平,严玉廷,等. 基于密度空间聚类和引力搜索算法的居民负荷用电模式分类模型[J]. 电力自动化设备,2018,38(1):129-136.
Su Shi,Li Kangping,Yan Yuting,et al. Classification model of residential power consumption mode based on DBSCAN and gravitational search algorithm[J]. Electric Power Automation Equipment,2018,38(1):129-136 (in Chinese).
[3] 赵 莉,候兴哲,胡 君,等. 基于改进K-means算法的海量智能用电数据分析[J]. 电网技术,2014,38(10):2715-2720.
Zhao Li,Hou Xingzhe,Hu Jun,et al. Improved K-means algorithm based analysis on massive data of intelligent power utilization[J]. Power System Technology,2014,38(10):2715-2720(in Chinese).
[4] 杨俊闯,赵 超. K-Means聚类算法研究综述[J]. 计算机工程与应用,2019,55(23):7-14,63.
Yang Junchuang,Zhao Chao. Survey on K-means clustering algorithm[J]. Computer Engineering and Applications,2019,55(23):7-14,63(in Chinese).
[5] Chen J,Zhang D,Nanehkaran Y A. An economic operation analysis method of transformer based on clustering[J]. IEEE Access,2019,7:127956-127966.
[6] Azimi R,Ghofrani M,Ghayekhloo M. A hybrid wind power forecasting model based on data mining and wavelets analysis[J]. Energy Conversion & Management,2016,127(1):208-225.
[7] Wang Xin,Lee Wei-Jen,Huang Heng,et al. Factors that impact the accuracy of clustering-based load forecasting[J]. IEEE Transactions on Industry Applications,2016,52(5):3625-3630.
[8] 赵文清,龚亚强. 基于Kernel K-means的负荷曲线聚类[J]. 电力自动化设备,2016,36(6):203-207
Zhao Wenqing,Gong Yaqiang. Load curve clustering based on Kernel K-means[J]. Electric Power Automation Equipment,2016,36(6):203-207(in Chinese).
[9] 李 阳,刘友波,刘俊勇,等. 基于形态距离的日负荷数据自适应稳健聚类算法[J]. 中国电机工程学报,2019,39(12):3409-3420.
Li Yang,Liu Youbo,Liu Junyong,et al. Self-adaptive and robust clustering algorithm for daily load profiles based on morphological distance[J]. Proceedings of the CSEE,2019,39(12):3409-3420(in Chinese).
[10]李春燕,蔡文悦,赵溶生,等. 基于优化SAX和带权负荷特性指标的AP聚类用户用电行为分析[J]. 电工技术学报,2019,34(增1):368-377.
Li Chunyan,Cai Wenyue,Zhao Rongsheng,et al. Customer behavior analysis based on affinity propagation algorithm with optimized SAX and weighted load characteristic indices[J]. Transactions of China Electrotechnical Society,2019,34(Suppl 1):368-377(in Chinese).
[11]石季英,薛 飞,李雅静,等. 基于免疫二进制萤火虫算法的主动配电网低碳目标网架规划[J]. 天津大学学报(自然科学与工程技术版),2017,50(5):507-513.
Shi Jiying,Xue Fei,Li Yajing,et al. Active distribution system planning for low-carbon objective using immune binary firefly algorithm[J]. Journal of Tianjin University(Science and Technology),2017,50(5):507-513(in Chinese).
[12]张明锐,陈喆旸,韦 莉. 免疫萤火虫算法在光伏阵列最大功率点跟踪中的应用[J]. 电工技术学报,2020,35(7):1553-1562.
Zhang Mingrui,Chen Zheyang,Wei Li. Application of immune firefly algorithms in photovoltaic array maximum power point tracking[J]. Transactions of China Electrotechnical Society,2020,35(7):1553-1562(in Chinese).
[13]张 晗,杨继斌,张继业,等. 基于多种群萤火虫算法的车载燃料电池直流微电网能量管理优化[J]. 中国电机工程学报,2021,41(3):833-846.
Zhang Han,Yang Jibin,Zhang Jiye,et al. Multiple-population firefly algorithm-based energy management strategy for vehicle-mounted fuel cell DC microgrid[J]. Proceedings of the CSEE,2021,41(3):833-846(in Chinese).
[14]汤文亮,张 平,汤树芳. 基于精英反向学习的萤火虫K-means改进算法[J]. 计算机工程与设计,2019,40(11):3164-3169.
Tang Wenliang,Zhang Ping,Tang Shufang. Improved firefly K-means algorithm based on elite opposition-based learning[J]. Computer Engineering and Design,2019,40(11):3164-3169(in Chinese).
[15]李媛媛,魏 延,张文泷,等. 基于K-means的邻域结合随机吸引的萤火虫算法[J]. 重庆师范大学学报(自然科学版),2021,38(6):114-121.
Li Yuanyuan,Wei Yan,Zhang Wenlong,et al. The firefly algorithm based on K-means combining neighborhood and random attraction[J]. Journal of Chongqing Normal University(Natural Science),2021,38(6):114-121(in Chinese).
[16]陈小雪,尉永清,任 敏,等. 基于萤火虫优化的加权K-means算法[J]. 计算机应用研究,2018,35(2):466-470.
Chen Xiaoxue,Wei Yongqing,Ren Min,et al. Weighted K-means clustering algorithm based on firefly algorithm[J]. Application Research of Computers,2018,35(2):466-470(in Chinese).
[17]肖 琪. 基于优化K-means算法的电力负荷分类研究[D]. 大连:大连理工大学,2015.
Xiao Qi. Research on Power Load Classification Based on Optimized K-means Algorithm[D]. Dalian:Dalian University of Technology,2015(in Chinese).
[18]林诗洁,董 晨,陈明志,等. 新型群智能优化算法综述[J]. 计算机工程与应用,2018,54(12):1-9.
Lin Shijie,Dong Chen,Chen Mingzhi,et al. Summary of new group intelligent optimization algorithms [J]. Computer Engineering and Applications,2018,54(12):1-9(in Chinese).
Load Clustering Characteristic Analysis of the Distribution Network Based on the Combined Improved Firefly Algorithm and K-means Algorithm
Wang Jidong1,Gu Zhicheng1,Ge Leijiao1,Zhao Changwei2,Jia Dongqiang3
(1. Key Laboratory of Smart Grid of Ministry of Education(Tianjin University),Tianjin 300072,China;2. Chengdong Power Supply Branch,State Grid Tianjin Electric Power Company,Tianjin 300650,China;3. State Grid Beijing Electric Power Research Institute,Beijing 100075,China)
The load clustering analysis of distribution networks is the basis for customized power and high-quality and reliable power supply. However,the existing K-means clustering methods are limited by the data sample set and selection of the initial center of clustering,wherein selecting different initial centers will yield significantly different clustering results. Therefore,according to the characteristics of distribution network load data,a distribution network load clustering analysis method based on the combination of improved firefly and K-means algorithms is proposed. Benefiting from the strong global search ability of the firefly algorithm and considering the intraclass similarity and interclass differences,the initial center of the K-means algorithm is optimized to obtain the minimum value of the clustering effectiveness index of the results. Further,to mitigate the weakness of the firefly algorithm in processing load data by adding excellent first-generation individuals via the density method and using an improved attraction formula and a probability attraction between individuals to optimize the individual movement mode in the iterative process,the early convergence speed is accelerated,and the later convergence is stabilized. The algorithm approaches the extreme value faster with a faster calculation speed. This paper lists several examples to verify the clustering effect of the proposed algorithm and finds the optimal initial center of the K-means algorithm for the power load data of a distribution station area,thus obtaining the minimum Davies-Bouldin index,reducing the intraclass loading clustering differences and increasing the interclass differences. The final clustering center exhibits highly representative characteristics,thus providing a basis for load type division and clustering characteristic analysis and laying the foundation for differentiated power service customization on the demand side.
distribution network load;K-means clustering;firefly algorithm;data-driven method
10.11784/tdxbz202201006
TM76
A
0493-2137(2023)02-0137-11
2022-01-07;
2022-06-30.
王继东(1977— ),男,博士,教授,jidongwang@tju.edu.cn.
葛磊蛟,legendglj99@tju.edu.cn.
国家自然科学基金资助项目(No.51807134);国网天津市电力公司科技资助项目(KJ21-1-18).
Supported by the National Natural Science Foundation of China(No. 51807134),State Grid Tianjin Electric Power Company Science and Technology Project(No. KJ21-1-18).
(责任编辑:孙立华)
