考虑时变磨损的机器人磨抛参数优化研究

王 超，郑乾健，肖聚亮，周 宇，刘海涛，黄 田

考虑时变磨损的机器人磨抛参数优化研究

王 超1, 2，郑乾健1，肖聚亮1，周 宇1，刘海涛1，黄 田1

(1. 天津大学机械工程学院，天津 300354；2. 潍柴动力股份有限公司工艺工匠研究院，潍坊 261061)

针对自动化磨抛过程中存在的磨抛工具磨损现象，使得难以建立精准的磨抛去除模型进而达到稳定一致的磨抛效果这一问题，提出了一种考虑时变磨损的机器人磨抛参数优化方法．首先，将物理建模方法中的丰富信息和回归建模方法的跟踪学习特性相结合，提出了一种融合先验知识的磨抛材料去除回归模型，极大地减少了原本回归模型所需的大量实验数据，使得提出的模型能够跟踪砂纸的磨损变化；其次，将所使用模型的预测结果与其他文献所提出的理论模型以及基于支持向量回归的预测模型进行了对比分析；最后，使用所得的预测模型对机器人磨抛参数进行优化，在混联机器人抛光实验台上进行实验验证，结果表明，所提出的融合先验知识的磨抛材料去除模型相比于常用模型具有更高的预测精度和更少的实验数据，所提出的机器人磨抛参数优化方法能够有效地补偿磨抛工具的磨损，保证磨抛过程中材料去除的一致性，同时提高了磨抛加工效率．

时变磨损；支持向量回归；材料去除模型；参数优化

模具磨抛精加工在整个制造所费时间中的占比较大，约占37%[1]．其目的是为了降低工件表面的粗糙度，同时在一定程度上去除模具成型时形成的凹凸层及裂纹层，即刀纹，并修复工件表面的面型误差，以期获得所要求的形状、尺寸、位置精度和表面粗糙度．传统的模具打磨和抛光主要是依赖于熟练工人的手工加工，是一种低效率重复性的劳动，且随机性较大，很难保证加工质量的稳定性和一致性[2]．此外，磨抛作业的环境噪音大，工人暴露在磨抛加工的粉尘中，对其健康也会造成严重的影响[3]．因此开展磨抛自动化的研究是具有重要意义的．

在自动化磨抛过程中，机器人可以使用多种抛光工具对不同类型的工件进行抛光，通过调控抛光力、主轴转速、进给速度等参数进行稳定和均匀的去除，但是如何正确综合地处理这些因素以达到在保证加工效果的情况下效率最大化始终是一个难点，这需要建立准确的磨抛去除模型来作为综合调控的依据．此外，由于加工过程中磨抛工具存在不可避免的磨损现象，其磨损程度对磨抛去除量的影响很大，其动态变化的特性对建立准确的磨抛去除模型进而达到恒定均匀的磨抛效果造成了很大的阻碍．目前主要有两类磨抛建模方法：一为物理建模方法；二为回归建模方法．

回归建模方法指的是通过选择可观测的关键影响因素作为输入，选择合适的建模指标作为输出，利用数学统计和机器学习的方法训练磨抛的数学模型．国内外在这方面的研究较少．浙江大学冯海涛[8]以砂带速度、机器人进给速度和工件曲率为输入，以加工后的粗糙度为因变量，建立了基于支持向量回归的粗糙度预测模型，根据不同的抛光参数对加工后的表面粗糙度进行分析和预测，但是该模型并没有考虑磨抛工具磨损的影响，且没有从材料去除的角度考虑．Yue等[9]提出了一种基于支持向量回归的磨削深度预测模型，其模型根据现场测量数据对模型进行修正，能够在一定程度上适应环境的变化如砂带的逐渐磨损、新的待加工工件等，但是为了得到较佳的模型，实验需要收集大量训练用数据，实验所需时间和花费较大．Pandiyan等[10]使用田口实验确定的磨抛参数对不同的统计回归方法进行评估，得出砂粒尺寸对材料去除的影响最大，但是没有考虑到磨抛过程中砂粒尺寸会因磨损而变化．相较于物理建模的方法而言，使用回归建模是一种更能有效评估磨损变化的建模方法，其能够利用实验数据，抓住主要变量．但是现有的回归建模方法所采用的“黑箱子”式的算法，基本没有利用已有物理理论模型的物理、几何知识，这导致回归模型输入的维度较大(包括主轴转速、进给速度、磨抛压力、磨抛角度、磨抛工具半径、工件表面曲率、磨抛时间等)，为了得到较为精准的去除模型，每个维度的数据必须要有一定的密度，因此回归所需的数据量呈指数级上升．而在实际的工作过程中，由于需要测得的数据点和数据类型较多，所需的实验时间是非常巨大的，这显然与实际制造加工的要求不符．清华大学吕洪波等[11]创新性地提出了融合先验知识的建模方法，基于半经验公式生成虚拟样本从而解决回归建模中所需样本数量过多的问题，但是在该文中将半经验公式中的磨削系数以及磨削压力、工件进给速度、砂带速度的次数均作为全局系数，即在整个磨削过程中保持不变，其适应性较差.

针对上述两种磨抛模型建模方法的优缺点，并且受文献[11]的启发，本文提出了一种融合先验知识的材料去除回归模型，将基于机理的物理建模方法包含的大量关于磨抛问题的信息利用起来，极大地减少了回归建模方法所需要的实验数据量；将回归建模方法中使用的机器学习方法跟踪磨抛工具磨损程度变化的优势利用起来，对理论模型中的Preston参数进行跟踪学习，使得最终的模型能够反映磨损的变化过程．最后，根据所提出的融合先验知识的材料去除回归模型，建立了一种机器人磨抛参数优化框架，对磨抛参数进行了优化，使得磨抛工具彻底失效之前尽可能加工更多的表面，并达到较为一致的抛光效果和材料去除深度．

1 机器人磨抛参数优化框架

本文构建的机器人磨抛参数优化框架主要包括3部分：数据收集、模型建立、参数优化实验．框架如图1所示．

图1 机器人磨抛参数优化框架

在数据收集部分，由于加工工件的磨抛质量受到多种因素影响，因此需要对磨抛模型中可控可观测的参数进行获取，如主轴转速、机器人加工进给速度、磨抛力等．此外为了评估磨抛效果，需要对工件表面材料去除深度、砂纸表面形貌信息进行采集，对被加工表面的表面粗糙度进行测量．

在模型建立部分，把磨抛去除理论模型中磨抛参数间的关系作为先验知识，使用支持向量回归的方法对理论模型中的Preston系数进行回归，实现在较少实验数据量下能够精准地预测磨抛的材料去除量．

在参数优化部分，本文针对进给速度进行优化，保持磨抛压力、主轴转速等参数为恒定，结合混联机器人连杆模具抛光实验台进行实验，将其与参数优化前的样件进行对比，验证了本文所提出的机器人磨抛参数优化方法的有效性．

2 融合先验知识的材料去除回归模型

考虑时变磨损的材料去除回归模型将物理理论模型与回归模型的优点相结合，将理论材料去除模型中的常数项Preston系数转变为随磨抛过程进行而变化的时变函数，把理论模型中磨抛力、进给速度、主轴转速等内在关系作为回归模型的先验知识，使用回归的方法量化在磨抛进程中磨抛工具磨损的影响，进而准确计算磨抛进程中的材料去除量，为机器人磨抛参数优化打下基础．

2.1 模型建立基础

Preston方程于1927年提出[12]，被广泛应用在磨抛加工中，它将磨抛去除深度描述为

由于实际机器人控制抛光实验采用控制抛光盘沿着抛光轨迹连续进给的方式，因此采用速度驻留形式的普雷斯顿方程，将式(1)改写为沿抛光路径的微分形式，即

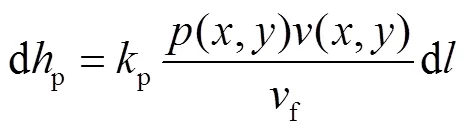
式中f表示抛光盘沿轨迹的进给速度．

根据文献[13]所做的研究，如图2所示，当抛光盘沿直线在平面上运动，进给方向为方向，抛光区域内一点(，)的压强为

图2 抛光盘沿直线进给时的速度分布

式中：n表示抛光盘的法向正压力；p表示抛光盘的半径．

(，)的相对线速度分布为

由于机器人的磨抛加工是一个累积过程，抛光盘在抛光接触区域某一点(，)的磨抛加工可以看作是从2点到1点的累加，因此可以得到抛光盘沿轨迹的普雷斯顿方程，即

通过实验对Preston系数p的测定，能够得到新磨抛工具较为精准的磨抛模型．但是在实际磨抛进程中，磨抛工具会快速磨损直至失效，随着磨抛工具表面形貌的迅速变化，Preston系数p也会随之变化，使得磨抛模型失效．故需要从方法的角度跟踪学习磨抛磨损这一变化过程，量化磨抛工具随时间磨损的程度．本文采用支持向量回归的方法对其进行量化和建模．

2.2 模型建立

2.2.1 支持向量回归算法原理

支持向量机(support vector machine，SVM)算法最早是由Cortes等[14]提出的最大化间隔的分类算法，当其用于回归问题时称作支持向量回归(support vector regression，SVR)，由Drucker等[15]提出．机器人磨抛去除模型建模是一个非线性回归问题，对于非线性回归，SVR采用的方式是先把样本点映射到高维空间，然后用高维空间中的线性超平面进行近似．对于给定数据

SVR问题的优化目标为

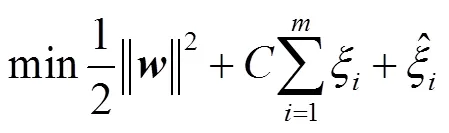
其限制条件为

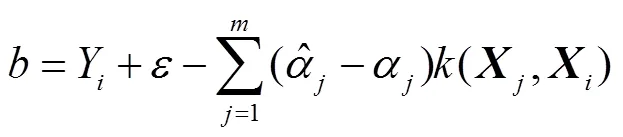
2.2.2 量化磨损及磨抛深度预测

为了获取模型构建所需要的实验数据，在混联机器人抛光实验台进行实验，采用Nanovea 白光干涉三维轮廓仪对试件轮廓进行采集．如图3(a)所示，由于受到轮廓仪的采集限制，实验试件设计为长宽均为80mm、材质为5CrNiMo的平面钢板．如图3(b)所示，在实际实验过程中，为保证磨抛过程的连续性，将3块试件并排放置进行实验．

图3 实验试件与安装

如图4所示为实验流程框图，具体包括以下5个步骤.

步骤1 针对并排固定的3块试件做如图5所示的轨迹规划，图5中1为磨抛轨迹的起始点，2为磨抛轨迹的终点，箭头方向即为磨抛进给方向．

步骤2 使用Nanovea 白光干涉三维轮廓仪获取砂纸初始表面反射光强度分布，该分布可以作为评价砂纸磨损程度的一个指标[16]，同时使用三维轮廓仪扫描获取工件表面的初始轮廓高度．3块钢板的测量范围分别为图5中的点至点、点至点、点至点．

步骤3 在单次实验中，同一次磨抛保持法向磨抛力和进给速度恒定．表1表示各组实验数据中相同的参数或设置．表2为实验数据记录样例．

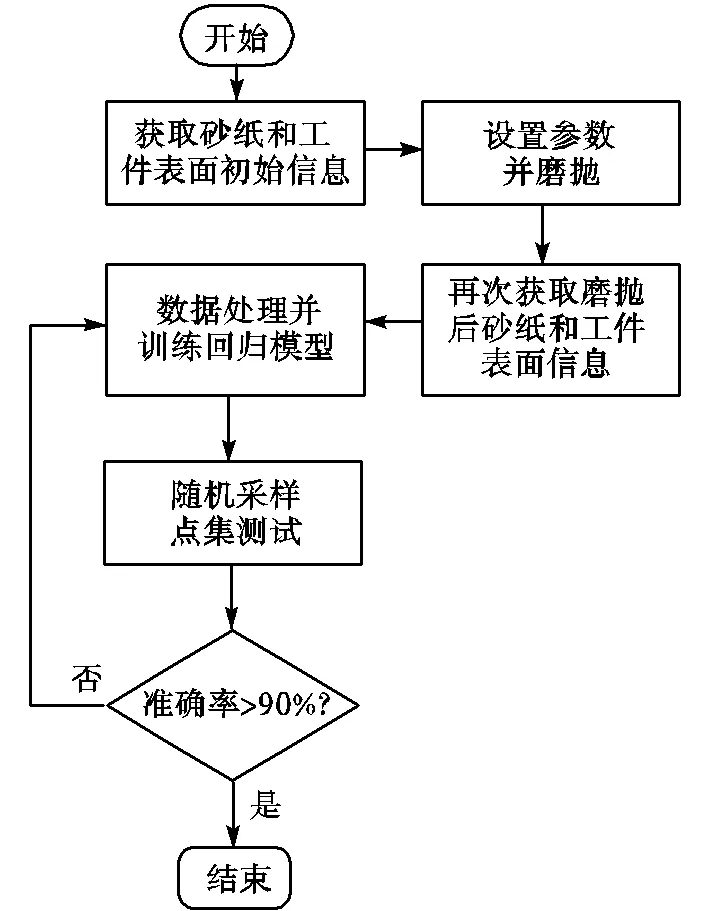
图4 实验流程

图5 实验轨迹规划

表1 各组实验相同的参数

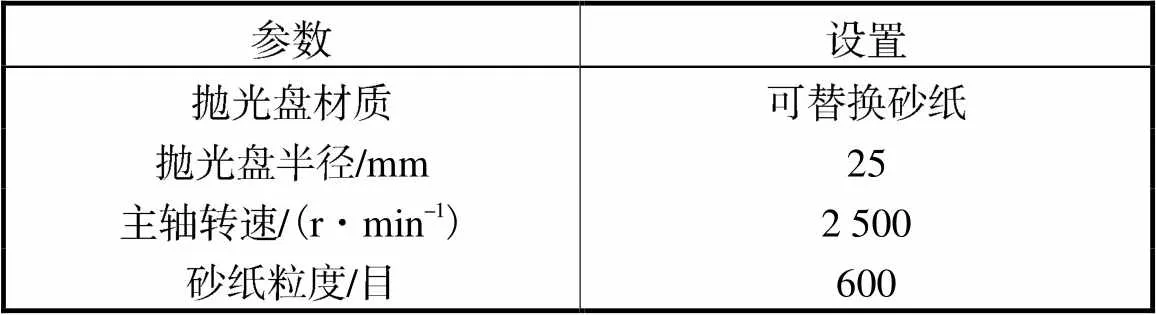
Tab.1 Same parameters in each group of experiments

表2 实验数据样例

Tab.2 Sample experimental data

图6 试件磨抛前后表面形貌

在训练SVR回归模型前，将式(10)作为先验知识输入至模型中，使得磨抛去除深度hp与时间的变化关系转化为Preston系数与时间的变化关系，进而简化了问题．同时，由于该回归问题为关于时间序列的预测问题，因此不采用常用的K折交叉验证方法，而采用扩展窗口交叉验证方法寻找最优的超参数组合[17]．当实际测量计算得到的磨抛去除深度与SVR模型回归预测得到的去除深度两者之间的差值在区间内，则认为SVR模型在该点的预测是正确的．图7中的训练准确率指的是数据集中SVR预测正确的点数量在数据集中所占的比重．考虑到由于测量时试件存在污渍或测量设备振动等一些其他情况，使得实验会得到明显偏离理想值的一些“坏点”，因此当准确率大于90%时，即认为训练得到的模型是可行的．

图8 Preston系数变化曲线

表3 SVR参数

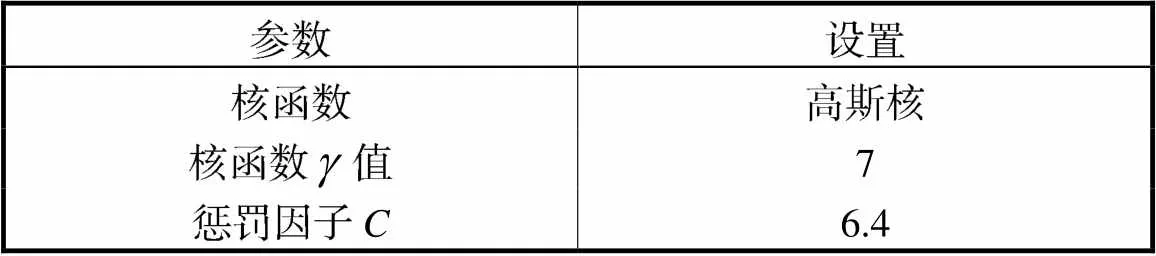
Tab.3 SVR parameters

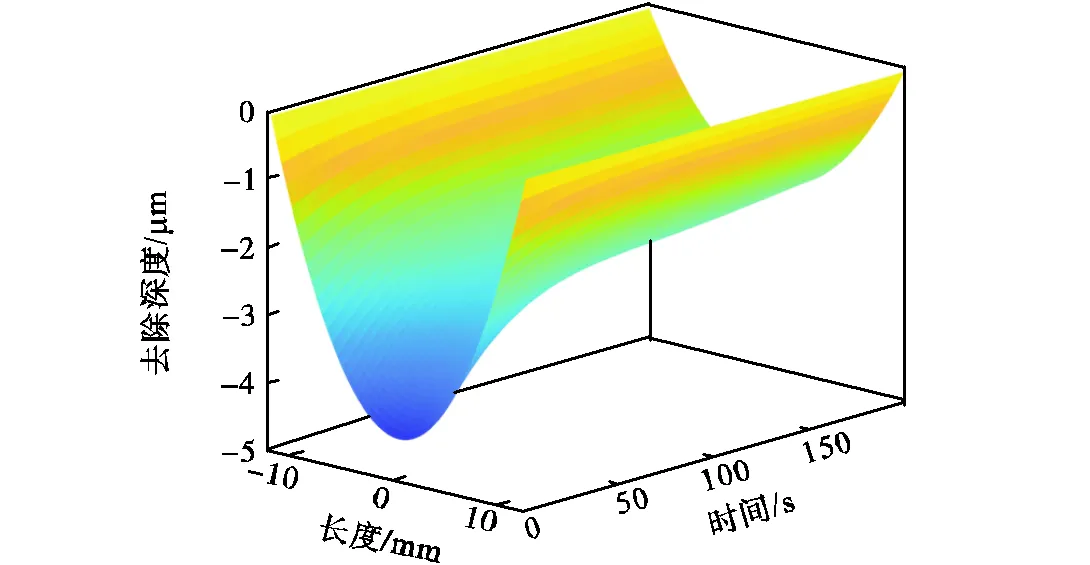
图9 一定工况下的材料去除深度预测

此外，通过多组磨抛参数组合实验发现，当磨抛压力较低(10～25N)时，砂纸的磨损速度很慢，但是磨抛的效果也很差，当磨抛压力提高到一定程度(30～50N)时，由于在高磨抛力下砂纸的表面磨粒快速磨损，砂纸快速进入磨损稳定期，并且磨损速率趋于一致，与文献[18]所得出的结论是一致的．进给速度在1～4mm/s的范围内时，其变化对砂纸磨损速率的影响非常小，与文献[19]通过对不同磨抛参数的相对灵敏度分析得出砂带磨损速率对进给速度变化的敏感度最低的结论相一致．主轴转速的变化对砂纸的磨损速度有较大的影响，当主轴转速过大时，砂纸将快速磨损至失效，难以持久作业；当主轴转速过小时，虽然磨抛盘的磨损减缓，但是磨抛效果较差．综上，可以通过对进给速度与磨抛压力在一定范围内的调整优化来补偿磨抛盘的磨损．同时，为达到更佳的磨抛效果，也需要确定较佳的主轴转速．

2.2.3 模型对比分析

为了确定本文方法在预测效果良好的前提下所需要的训练样本数量，使用不同训练样本数量对本文方法，即融合先验知识的SVR方法进行训练，每50个数据点为一组，训练样本数分别为150、300、450、600．从除训练集外的5组实验组中随机抽取40个数据点作为测试集(每组抽取8个数据点)，使用训练出来的模型进行预测，在结果输出中，先将测试集按照实测值从小到大进行排列．如图10所示为使用不同训练样本数量训练得到的模型在测试样本中的预测值与实测值的对比．从图10中可以看出，训练样本数量为150的模型其预测效果已经较为优秀，随着训练样本数量的增加，几种模型的预测性能相差无几．考虑到减少实验成本和时间，使用样本数量为150的样本集即可满足预测效果，之后使用该模型与其他算法进行比对．

图10　　本文方法在不同训练样本下的预测值与实测值的对比

图11 预测结果与实测值结果对比

表4 误差分析结果对比

Tab.4 Error analysis and comparison results

根据图11与表4可以看出，理论模型由于其Preston计算方法以及未考虑磨损的原因，其大部分预测值相较于实测值都较大，偏离程度取决于磨抛加工时间的长短；训练样本数量为600的原SVR方法在一定程度上也能够预测出磨抛去除深度，但是在部分数据点上的预测值与实测值有较大偏离，本文方法的SSE、RMSE、MAPE、MAE相较于使用训练样本数量为600的原SVR方法分别降低了0.6652μm2、0.0712μm、1.36%、0.0424μm，均是本文所提出的融合先验知识的SVR方法更为优秀，分析其原因在于原SVR方法的输入矩阵维度较大，而训练样本的数量仅有600，样本对于磨抛参数的分布而言是较为稀疏的，训练样本数不够，导致原SVR方法对于未知样本的预测能力较差．而当训练样本数增至1200时，通过表4可以发现原SVR方法与本文所提出的融合先验知识的SVR方法的误差评价指标相差不大，综合考虑测量误差、加工误差等其他因素，可以认为两者的预测能力基本一致，但是本文方法训练样本数量仅为150，样本数量远少于前者．综上，融合先验知识的磨抛材料去除模型能够较好地量化评估磨抛工具的磨损并得到较佳的磨抛深度预测效果，在小样本预测方面具有优越性，大大减少了实验所需要的时间和经济成本．

3 考虑时变磨损的机器人磨抛参数优化实验

为保证材料去除的一致性以及提高磨抛的效率，需要通过改进磨抛参数对磨抛工具的磨损进行补偿．较为常用的可控可观测磨抛参数为磨抛进给速度f和磨抛压力n，可以只调控某一磨抛参数如进给速度f(或磨抛压力n)，也可以为了实现磨抛时间最短、磨抛参数的调控尽可能平滑等目标，同时调控进给速度f和磨抛压力n．为了简单起见，将磨抛压力n设为常数，只调控磨抛进给速度f来保证较好的磨抛去除效果．设定磨抛深度为3μm，给定法向力为40N．为了便于工程实际应用和计算，使用图8中折线2所示的p变换关系，通过反算进给速度f可以得到如图12所示的进给速度优化曲线．

图12 进给速度优化曲线

使用优化后的磨抛参数在混联机器人抛光实验台进行实验，如图13(a)所示．待加工工件表面的微观形貌，如图13(b)所示，表面可见有明显密集的刀纹. 经过参数调控磨抛后工件表面的微观形貌，如图13(c)所示，几乎不可辨加工方向．

同样使用白光干涉三维轮廓仪对试件表面进行检测获取磨抛过程中的去除深度．若使用文献[12]所述理论模型，当设定磨抛深度为3μm，给定法向力为40N，则可计算得到磨抛过程中的进给速度为2.4mm/s，为一定值．使用理论模型未经过优化的进给速度所测得的磨抛去除深度以及参数优化后测得的磨抛去除深度与期望值的对比，如图14所示，从图14中可以看出，未经过优化的进给速度所测得的磨抛去除深度在磨抛初期略大于3μm，而随着磨抛工具的磨损，其去除深度逐渐减小并且始终小于3μm，无法在全过程中保持材料去除的一致性．而经过参数优化后的实验组其磨抛去除深度在全过程中与期望值较为一致，能够较好地补偿砂纸的磨损，保证材料去除量的一致性．

图13 磨抛前后工件表面微观形貌对比

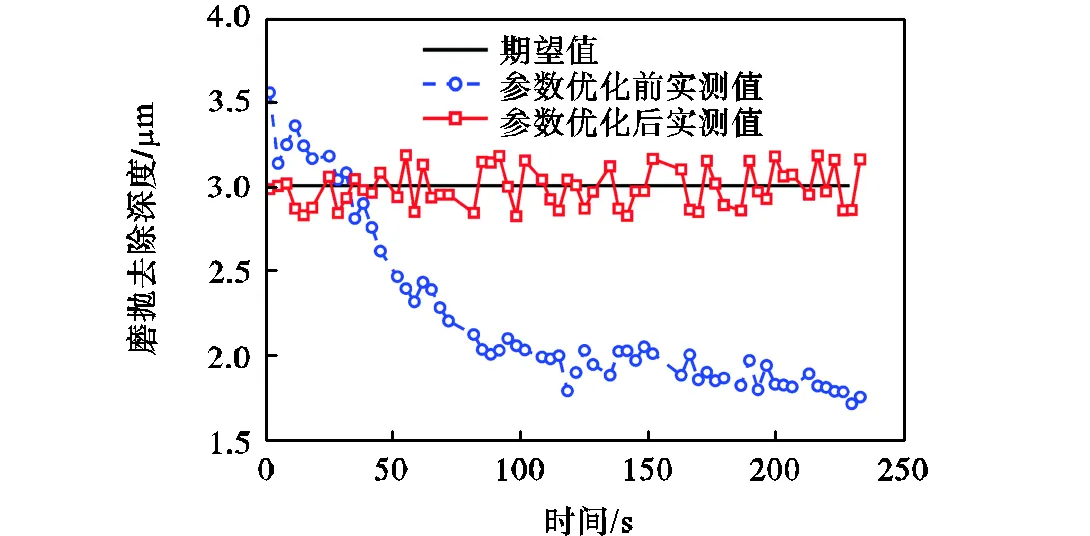
图14 参数优化前后磨抛去除深度与期望值对比

此外使用北京时代TR200高精度表面粗糙度仪分别测量磨抛时间为10s、20s、30s、120s、130s、140s、230s、240s、250s处试件的表面粗糙度，图15所示为磨抛参数优化前后在这9个采样点处表面粗糙度的大小，从图15中可以看出，经过参数优化后的实验组虽然在磨抛初期其表面粗糙度比未经过参数优化的实验组更大，但是其磨抛效果在全过程中较为一致，整体上磨抛效果更佳，在满足表面粗糙度要求的情况下能够加工更长的时间，而未经参数优化的实验组其磨抛效果由于砂纸磨损而快速下降，在大部分时间的磨抛效果均劣于经过参数优化后的实验组，在230s后的表面粗糙度明显大于参数优化后的实验组．

图15 参数优化前后表面粗糙度对比

综上，从磨抛去除深度和表面粗糙度两个角度证明了本文所提出的磨抛参数优化方法能够较好地补偿砂纸磨损，进而提高砂纸的利用率和提高磨抛效率，是一种切实有效的机器人磨抛参数优化方法．

4 结 语

本文提出了一种考虑时变磨损的机器人磨抛参数优化方法．首先将理论模型中材料去除深度与磨抛参数之间的关系作为先验知识，融合回归模型能够跟踪学习磨抛磨损变化情况的特性，提出了一种融合先验知识的磨抛材料去除模型，极大地减少了回归模型所需的数据维度和数据数量，方便工程实际应用．通过与传统SVR方法与传统理论模型进行对比分析证明了融合先验知识的SVR模型能够用来预测磨抛去除深度，并且在小样本预测上具有显著优势．根据提出的去除模型优化机器人磨抛参数，并在混联机器人抛光实验台进行实验，实验证明所提出的考虑时变磨损的机器人磨抛参数优化方法能够较好地补偿磨抛工具的磨损，使得磨抛去除量在全加工过程中较为一致，磨抛加工效果更佳，此外在满足表面粗糙度要求的情况下能够加工更长的时间，进而提高了磨抛工具的利用率和磨抛效率．

［1］ Saito K. Finishing and polishing of free-form surface[J]. Bulletin of the Japan Society of Precision Engineering，1984，18(2)：104-109.

［2］ Kamijyo K，Sakamoto M，Asao T，et al. Development of an automatic polishing system for metal molds and dies(1st report，automation of polishing operation based on CAD/CAM data)[J]. Transactions of the Japan Society of Mechanical Engineers Series C，1989，55(509)：193-196.

［3］ Mohammad A，Wang D. Electrochemical mechanical polishing technology：Recent developments and future research and industrial needs[J]. International Journal of Advanced Manufacturing Technology，2016，86：1-16.

［4］ 曾 晰. 软固结磨粒气压砂轮设计方法及材料去除特性研究[D]. 杭州：浙江工业大学机械工程学院，2013.

Zeng Xi. Research on the Design Method and Material Removal Characteristics of the Soft-Consolidated Abra-sive Grain Pneumatic Grinding Wheel[D]. Hangzhou：School of Mechanical Engineering，Zhejiang University of Technology，2013(in Chinese).

［5］ Cao Z C，Cheung C F. Multi-scale modeling and simulation of material removal characteristics in computer-controlled bonnet polishing[J]. International Journal of Mechanical Sciences，2016，106：147-156.

［6］ 朱天宝，金晓怡，陈志鹏，等. 复杂曲面柔性抛光材料去除模型研究[J]. 组合机床与自动化加工技术，2020(9)：76-79.

Zhu Tianbao，Jin Xiaoyi，Chen Zhipeng，et al. Study on material removal model for flexible polishing of complex surfaces[J]. Modular Machine Tools and Automatic Machining Technology，2020(9)：76-79(in Chinese).

［7］ Huang H，Gong Z M，Chen X Q，et al. Robotic grinding and polishing for turbine-vane overhaul[J]. Journal of Materials Processing Technology，2002，127(2)：140-145.

［8］ 冯海涛. 机器人自动化拋光系统关键技术的研究[D]. 杭州：浙江大学机械工程学院，2015.

Feng Haitao. Research on Key Technologies of Robot Automatic Polishing System[D]. Hangzhou：School of Mechanical Engineering，Zhejiang University，2015(in Chinese).

［9］ Yue Y，Zhang J，Zhou Y，et al. Inverse input predic-tion model for robotic belt grinding[J]. International Journal of Intelligent Robotics and Applications，2021，5(4)：465-476.

［10］Pandiyan V，Caesarendra W，Glowacz A，et al. Modelling of material removal in abrasive belt grinding process：A regression approach[J]. Symmetry，2020，12(1)：363-380.

［11］吕洪波，宋亦旭，贾培发. 机器人修磨中融合先验知识的适应学习建模方法[J]. 机器人，2011，33(6)：641-648.

Lü Hongbo，Song Yixu，Jia Peifa. Adaptive learning modeling method incorporating prior knowledge in robot grinding[J]. Robot，2011，33(6)：641-648(in Chi-nese).

［12］ Preston F W. The theory and design of glass plate polishing machine[J]. Journal of the Society of Glass Technology，1927，11：214-256.

［13］樊 成，赵 继，张 雷，等. 移动抛光自由曲面材料去除的理论建模与试验研究[J]. 机械工程学报，2014，50(5)：173-181.

Fan Cheng，Zhao Ji，Zhang Lei，et al. Theoretical modeling and experimental research on material removal of free-form surface in mobile polishing[J]. Journal of Mechanical Engineering，2014，50(5)：173-181(in Chinese).

［14］ Cortes C，Vapnik V. Support vector networks[J]. Machine Learning，1995，20(3)：273-297.

［15］ Drucker H，Burges C，Kaufman L，et al. Support vector regression machines[J]. Advances in Neural Information Processing Systems，1997，28(7)：779-784.

［16］ He Z，Li J Y，Wu Y F，et al. Quantitative study on abrasive belt wear based on geometric parameters[J]. Key Engineering Materials，2018，764：156-163.

［17］Bergmeir C，José M B. On the use of cross-validation for time series predictor evaluation[J]. Information Sciences，2012，191：192-213.

［18］Yang C，Huang Y，Huang Z，et al. Experimental research on the abrasive belt grinding 1Cr13 stainless steel[J]. Mechanical ence and Technology for Aerospace Engineering，2011，30(6)：1007-1010，1015.

［19］ Lin X，Xin X，Shan X，et al. Optimal parameter ranges of material removal depth of abrasive cloth wheel polishing based on sensitivity analysis[J]. The International Journal of Advanced Manufacturing Technology，2019，105(12)：5165-5179.

Research on Optimization of Robot Grinding and Polishing Parameters Considering Time-Varying Wear

Wang Chao1, 2，Zheng Qianjian1，Xiao Juliang1，Zhou Yu1，Liu Haitao1，Huang Tian1

(1. School of Mechanical Engineering，Tianjin University，Tianjin 300354，China；2. Craftsman Research Institute，Weichai Power Co.，Ltd.，Weifang 261061，China)

Addressing the problem of grinding and polishing tool wear in the automatic grinding and polishing process，an issue that makes it difficult to establish an accurate grinding and polishing removal model to achieve a stable and consistent grinding and polishing effect，a robot grinding and polishing parameter optimization method considering time-varying wear is proposed. First of all，combining the rich information in the physical modeling method with the tracking learning characteristics of the regression modeling method，a regression model for grinding and polishing material removal that integrates prior knowledge is proposed. Such a model will greatly reduce the large amount of experimental data required. The proposed model can track the changes in grinding and polishing wear. The prediction results of the model used are compared with theoretical models and the support vector regression prediction model proposed in other research. Finally，the prediction model obtained is used to optimize the robot grinding and polishing parameters，and experimental verification is carried out on the polishing experiment platform of the hybrid robot. The results show that the proposed grinding and polishing material removal model fused with prior knowledge has higher prediction accuracy and less experimental data. The proposed optimization method for robot grinding and polishing parameters can effectively compensate for the wear of grinding and polishing tools，ensure the consistency of material removal in the grinding and polishing process，and improve the efficiency of grinding and polishing.

time-varying wear；support vector regression；material removal model；parameter optimization

10.11784/tdxbz202110006

TH162

A

0493-2137(2023)02-0127-10

2021-10-11；

2021-12-02.

王 超（1985—  ），男，博士研究生，wangchao4585@163.com.

郑乾健，2020201185@tju.edu.cn.

国家科技重大专项资助项目(2017ZX04021001-004)．

Supported by the National Science and Technology Major Project(No. 2017ZX04021001-004).

(责任编辑：王晓燕)