基于缩比模型的水下滑翔机运动相似性研究

刘玉红，冯登雪，邓仕晗，刘书赫，朱亚强

基于缩比模型的水下滑翔机运动相似性研究

刘玉红，冯登雪，邓仕晗，刘书赫，朱亚强

(天津大学机械工程学院，天津 300350)

利用水下滑翔机缩比模型预报原型运动特征及滑翔经济性的前提是两者运动相似．以天津大学自主研制的Petrel Ⅱ水下滑翔机作为研究对象，从相似理论出发，基于动力学方程及纳维-斯托克斯(N-S)方程，推导了水下滑翔机原型与模型在运动相似时应当满足相似准则以及相似转换关系．采用计算流体动力学方法计算了不同缩比情况下水下滑翔机的升力系数及阻力系数，得到了尺度相似比与升力系数、阻力系数的关系．分析表明，在稳定滑翔状态下，水下滑翔机缩比模型与原型运动相似需要满足弗劳德准则；在该准则下，在一定的缩尺比范围内，升力系数与阻力系数的尺度效应并不明显，以尺度相似比为0.5设计缩比模型最为合适．通过水池试验获得了缩比模型在一定俯仰角下的速度、升阻比等运动参数，试验结果表明：缩比模型与原型间存在运动相似性；缩比模型在水池试验中得到的横向速度、垂向速度和升阻比与水下滑翔机原型海试结果吻合较好，相对误差满足工程误差要求．论文提出的利用水下滑翔机缩比模型对原型运动参数和滑翔经济性进行预报切实可行，可为大型水下滑翔机的设计提供实验室验证平台，对于缩短研发周期具有重要意义．

水下滑翔机；缩比模型；相似理论；运动相似；滑翔经济性

良好的滑翔经济性是水下滑翔机初步设计阶段的优化目标之一，水下滑翔机的升阻比/是衡量水下滑翔经济性的指标[1]．受特征长度、水池大小等因素的限制，原尺度滑翔机滑翔经济性评估的相关试验难以进行．如果原尺度滑翔机经过一定比例的缩小后，仍然保持相同的滑翔经济性，那么可以利用缩比模型对原尺度滑翔机的经济性进行评估．而保证两者之间滑翔经济性相同的前提是两者的运动参数有特定的比例关系，即两者之间具有运动相似性．本文确定了缩比模型的尺度相似比，并验证缩比模型和原尺度水下滑翔机的运动相似性，为后续研究不同水动力外形下的升阻比奠定基础．

模型试验能够在复杂现象中突出问题的主要矛盾，有利于发现现象的内在联系，已广泛应用于潜艇等大型水下潜器的研发．自20世纪70年代，美国海军水面战中心[2-3]便开展了多艘缩尺比为1/20及1/4的潜艇自航模试验，以获取潜艇缩比模型的尺度效应，进而得到实艇的操纵性．近年来，英国国防科技公司[4]也进行了多次潜艇自航模试验研究，以获得水动力相关的验证数据．国内海军工程大学刘洋等[5]对潜艇自航模的内部自调节装置进行设计，以消除工装误差的影响．美国普林斯顿大学Berman[6]首次设计了相似比为1/4.47的Slocum水下滑翔机缩比模型，并依据雷诺准则进行风洞试验，得到升力、阻力、俯仰力矩系数随攻角的变化；美国华盛顿大学LaMothe等[7]把小型水下滑翔机作为测试平台，采用3种不同回归方法获取升力系数和阻力系数，从而选出最适用于研究传统滑翔机水动力性能的方法．

在以往的研究中，缩比模型通常用于研究水下潜器的水动力性能，而本文主要关注水下滑翔机的运动特性，提出了利用水下滑翔机缩比模型进行水池试验推导原尺度滑翔机运动参数的方法．首先，以天津大学自主研制的Petrel Ⅱ水下滑翔机[8]为原型，基于其动力学方程和N-S方程推导相似准则以确定缩比模型和原型各参数间的相似比，通过CFD仿真讨论尺度效应对水动力系数的影响从而确定尺度相似比，利用尺度相似比为0.5的模型试验样机进行水池试验，最后，将试验结果推导至原型，并与原型的海试数据进行对比，验证了缩比模型与原尺度水下滑翔机之间的运动相似性．

1 缩比模型相似准则

相似准则的推导方法通常有3种，即量纲分析法、方程分析法和定律分析法[9]．量纲分析法适用于现象所涉及的物理量全部已知的情况，这种方法的优点在于不必确定描述现象的方程，缺点在于所选物理量可能不足或存在冗余导致相似准则推导错误．方程分析法适用于描述现象的方程已知的情况，该方法具有清晰的解题步骤和严谨的推理过程．定律分析法适用于现象相关的物理量全部已知并能够分清主次的情况，这种方法看不出现象的内在联系和变化过程，具有一定的局限性．由于本文研究对象水下滑翔机的运动方程和流体运动控制方程已知，因此，本文采用方程分析法建立水下滑翔机原理与模型之间的相似准则．

1.1 运动相似准则

根据线性理论，参考鱼雷等水下潜器黏性流体动力的线性表示，可得滑翔机所受阻力、升力和俯仰力矩的表达式[10]为

如果缩比模型与原尺度滑翔机之间运动相似，那么缩比模型动力学方程与原尺度滑翔机动力学方程相同．原尺度水下滑翔机在垂直面运动的动力学方程[8]为

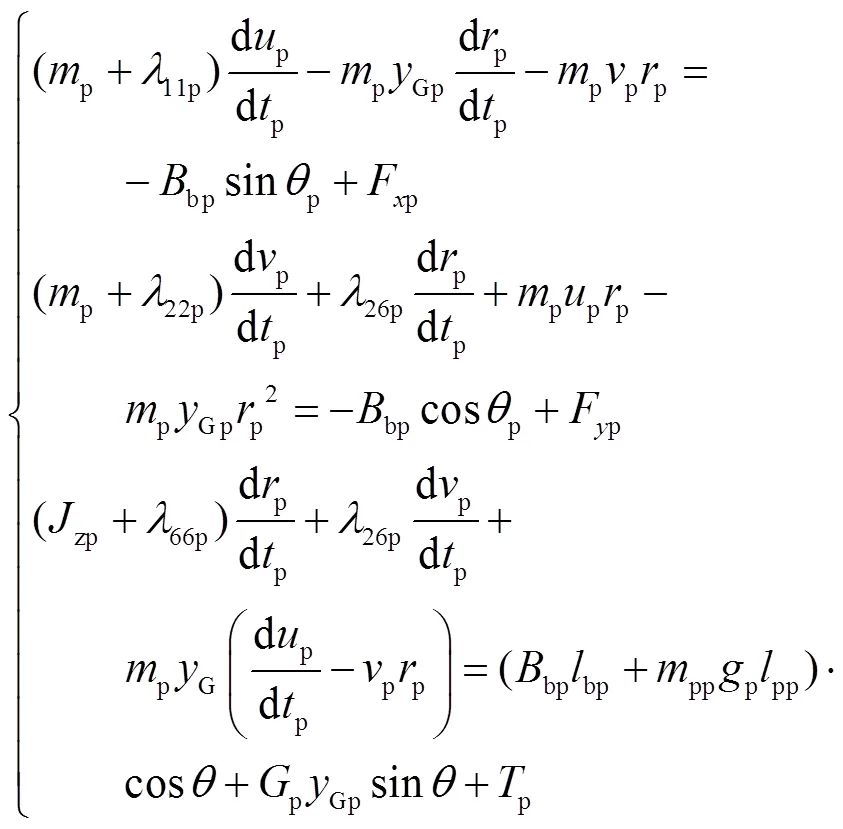
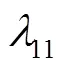
根据现象相似条件有以下相似变换，

式中：表示原尺度滑翔机与其缩比模型各参数的比例关系，称为相似比；下角标m表示与缩比模型相关的参数．将式(3)代入到式(2)得水下滑翔机缩比模型动力学方程为

将式(4)中的各项系数化为无量纲数，得到

由于缩比模型和原型方程形式相同，所以式(5)中各项系数为1，即有相似比关系式

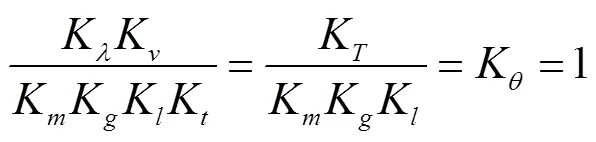
整理后，得到水下滑翔机原型与缩比模型运动相似的相似准则为

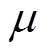
1.2 流动相似准则

水下滑翔机运动时会影响周围流场，除了考虑滑翔机运动的相似外，还要考虑流场的流动相似．利用上述方法，由描述水下滑翔机周围流体运动的控制方程推导出流动相似的相似准则．以二维向流动为例推导相似准则(向分析方法和结果与向相同)，对于水下滑翔机原型运动过程中其周围流场满足如下黏性不可压缩流体流动N-S方程：

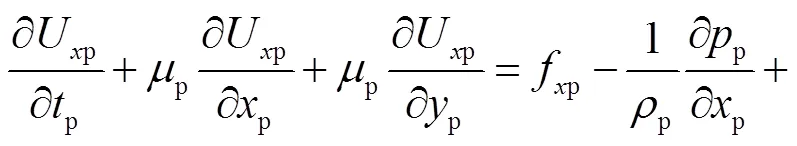
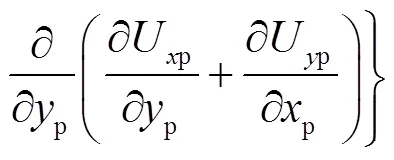
式中：为运动黏度；为黏性力；为压强．

则水下滑翔机原型与缩比模型周围流场各参数间的相似关系为

与第1.1节推导过程类似，将相似比代入式(9)可以得到以下相似准则：

式中为马赫数(Mach number)，表示惯性力与压缩力之比，说明流体压缩性的影响．式(10)说明，欲使水下滑翔机原型与模型周围流场流动相似，则需保证斯特劳哈尔数、马赫数、弗劳德数和雷诺数相同．

1.3 缩比模型相似准则

由第1.1节与第1.2节可知，研究水下滑翔机原型与其缩比模型的运动相似性需要满足的准则为斯特劳哈尔准则、时均准则、马赫准则、弗劳德准则和雷诺准则．由于水下滑翔机稳态滑翔时其运动速度较慢，一般为0.25～0.50m/s，且运动参数不随时间变化，流体也被认为是不可压缩流体，因此，本文中研究的水下滑翔机缩比模型相似准则可不考虑斯特劳哈尔准则、时均准则、马赫准则．

水下滑翔机稳态滑翔时，由于各运动参数不随时间变化，其在垂直面的动力学方程式(2)可简化为

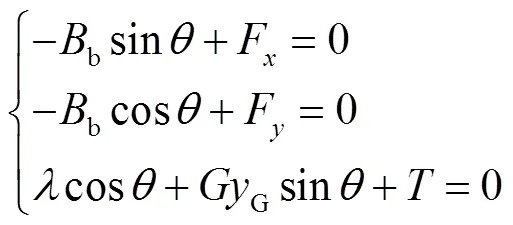
显然，式(12)和式(13)互相矛盾，不能同时满足.

滑翔机水动力系数会随雷诺数和弗劳德数的变化而变化．当满足雷诺准则时，原尺度水下滑翔机和缩比模型的雷诺数相等，此时，虽然能够保证原型和缩比模型的水动力系数相等，但根据式(13)，缩比模型的速度相似比与尺度相似比成反比，这就要求缩比模型的尺度越小时，速度反而越大，对于水下滑翔机来说，这是难以实现的．而在满足弗劳德准则时，原尺度水下滑翔机和缩比模型的弗劳德数相等，在这种情况下，若缩比模型的水动力系数和原型的水动力系数差异并不明显，则说明这种方法是可取的．

2 缩比模型设计

2.1 尺度相似比的确定

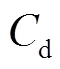
由图1可以看出，阻力系数随攻角减小而减小，随尺度相似比的减小而增大，在点K＝0.5前后分别服从两个不同的线性函数．当K在0.5～0.9时，阻力系数可以拟合为曲线＝−0.1179＋0.8098，相关性系数为0.9919；当K在0.3～0.5时，阻力系数可以拟合为曲线＝−0.3373＋0.9206，相关性系数为0.9998，即当K小于0.5时，阻力系数随尺度相似比的变化更加明显．由图2知，升力系数只随攻角的增加而增大，而尺度相似比的变化对升力系数基本没有影响．这是由于水流方向和水下滑翔机运动方向平行，与其所受升力方向垂直，当攻角一定时，滑翔机尺度增大，对升力及升力系数没有太大影响．

图1 不同攻角下阻力系数随尺度相似比的变化

图2 不同攻角下升力系数随尺度相似比的变化

图3 阻力系数偏差随尺度相似比的变化

2.2 缩比模型简介

水下滑翔机原型为实验室研制的Petrel Ⅱ水下滑翔机，如图4所示，缩比模型尺度相似比为0.5．表1列出了Petrel Ⅱ水下滑翔机原型与其缩比模型样机的主要参数．

依据Petrel Ⅱ水下滑翔机设计的缩比模型试验样机由6部分组成，如图5所示：浮力调节单元、控制单元、壳体、前后导流罩、机翼及尾翼．浮力调节单元由500mL注射器、TB6600两相步进驱动器及直流步进电机组成；其中，注射器与外界连通，当步进电机驱动注射器吸排水时，使得试验样机浮力改变，从而实现上浮和下潜．控制单元通过控制驱动器使电机运动，同时记录并保存数据．试验样机装有无线通讯模块，用于接收控制命令和传输数据．试验样机通过安装的十轴姿态角度传感器HWT901B采集其运动角度、加速度数据．

图4 Petrel Ⅱ水下滑翔机原型

表1缩比模型试验样机和原尺度滑翔机的主要特征参数

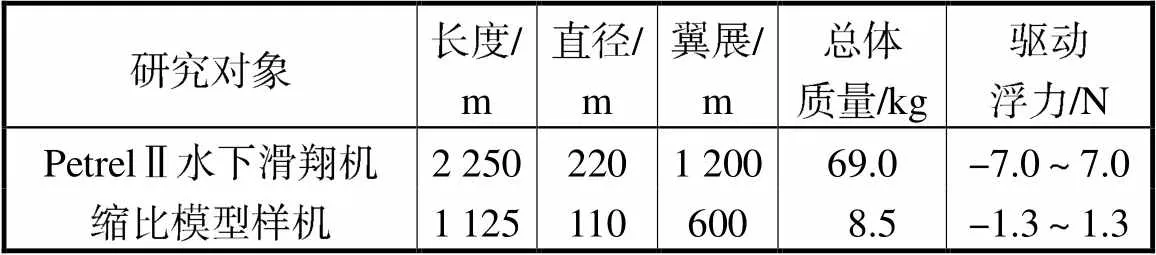
Tab.1　　Main characteristic parameters of the test proto-type of the scaled model and full-scale glider

图5 缩比模型试验样机结构

2.3 缩比模型初步验证

表2 缩比模型试验样机和原尺度滑翔机的水动力系数

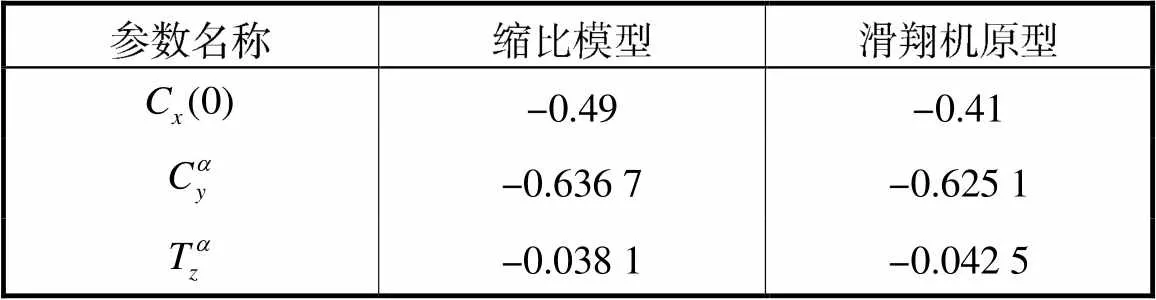
Tab.2　　Hydrodynamic coefficients of the test prototype of the scaled model and full-scale glider

表3缩比模型试验样机与原尺度滑翔机运动参数理论值对比

Tab.3　　Comparison of theoretical values of motion pa-rameters between the test prototype of the scaled model and full-scale glider

从理论计算的结果可以看出，缩比模型横向速度、垂向速度和升阻比的相对误差最大不超过10%，即尺度的缩小对于运动参数的影响在允许的误差范围内，说明0.5倍的缩比模型与原型具有良好运动相似性．

3 缩比模型样机试验验证

依据第2节缩比模型设计，研发缩比模型样机，如图6所示．

图6 缩比模型试验样机

模型试验在长13m、宽6m、深4.5m的水池中进行．试验过程如下：首先，令驱动器带动电机正转，浮力驱动单元开始吸水，当水量达到设定值时，停止吸水，此时，样机处于下潜状态；经过30s后，电机反转，浮力调节单元开始排水，样机转为上浮状态，当水量达到设定值时，停止排水；待样机浮出水面稳定后，则完成一个完整运动剖面．试验中，一个剖面的滑翔时间大约在60s左右．图7所示为滑翔机缩比模型试验样机上浮和下潜过程．

图7 试验样机纵垂面滑翔过程

将传感器采集到的试验样机水平加速度和垂直加速度转换到大地坐标系下，并进行积分得到试验样机的水平速度和垂直速度，如图8所示．再次积分便得到滑翔机水平位移和垂直位移，如图9所示．

下潜时，20s之前为浮力调节单元吸水阶段，为非稳态滑翔阶段；20～30s之间可以认为是稳态滑翔阶段，对这段时间内的俯仰角求取平均值为24.19°．30～44s为姿态调整阶段，44～57s为稳定的上浮阶段，这段时间内俯仰角的平均值为26.12°．由图8知，缩比模型样机稳态下潜阶段的水平方向平均速度为0.228m/s，垂直方向平均速度为0.100m/s；稳态上浮阶段的水平方向平均速度为0.191m/s，垂直方向平均速度为0.119m/s．由图9可以看出，缩比模型样机滑翔的最大水平方向位移为10.81m，最大垂直方向位移为2.63m．

由于稳态滑翔状态下，运动攻角很小，在试验中可忽略不计．由图8求得的各参数平均值乘以相应的相似比便可得到模型试验推导值，如表4所示．

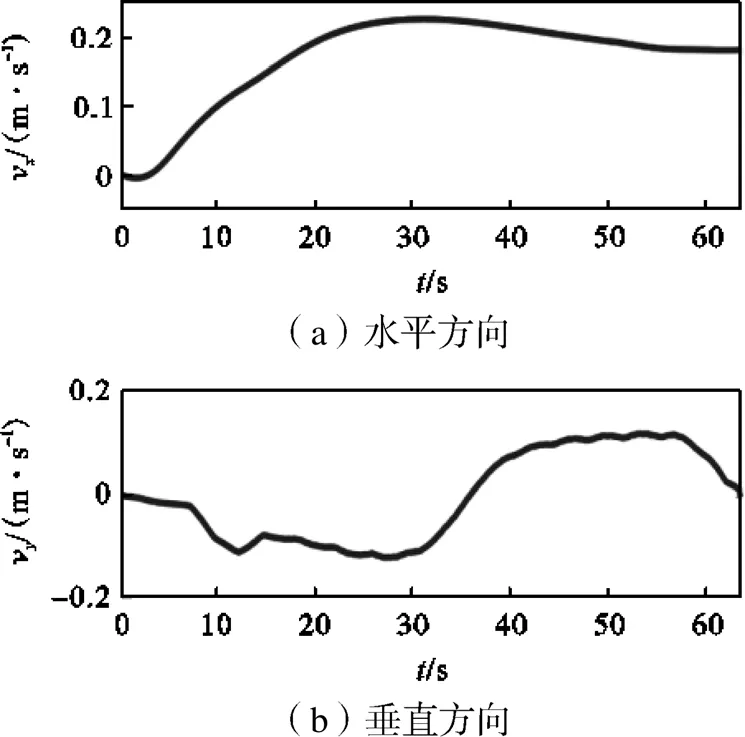
图8 水平和垂直速度变化曲线

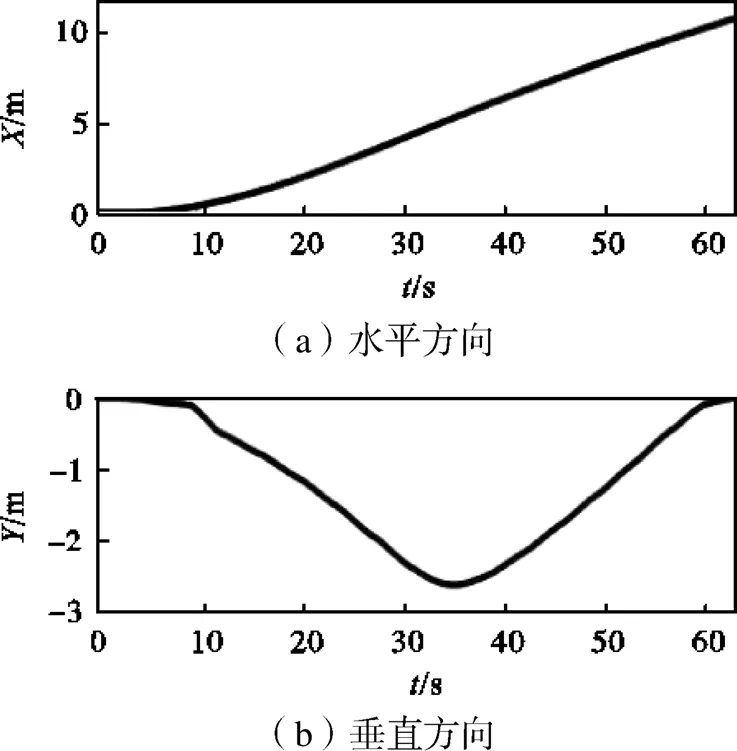
图9 水平和垂直位移变化曲线

图10和图11为Petrel Ⅱ水下滑翔机海试所得剖面位移及俯仰角变化情况，由此亦可求得其水平方向速度、垂直方向速度和升阻比．由于下潜阶段比较容易达到稳定状态，因此，这里只将下潜阶段数据进行对比，列于表4．

由表4结果可以看出，由模型推导出的原尺度滑翔机的运动参数与原型试验值的误差小于10%，误差均在可接受范围内，说明相似模型与原尺度滑翔机之间具有运动相似性，相似模型的推导结果可以为原尺度滑翔机的运动情况提供参考，并且可以由缩比模型的滑翔经济性对原型的滑翔经济性进行预报．原型试验值与模型试验推导值的误差主要源于两个方面：一方面是相似模型的尺度效应，即模型和实物之间不能满足全部的相似准则所带来的误差；另一方面是数值计算中水动力系数的计算误差、模型装配误差、制造误差和主要参数的测量误差等．

表4缩比模型与原型各运动参数与性能试验结果对比(稳态下潜滑翔阶段)

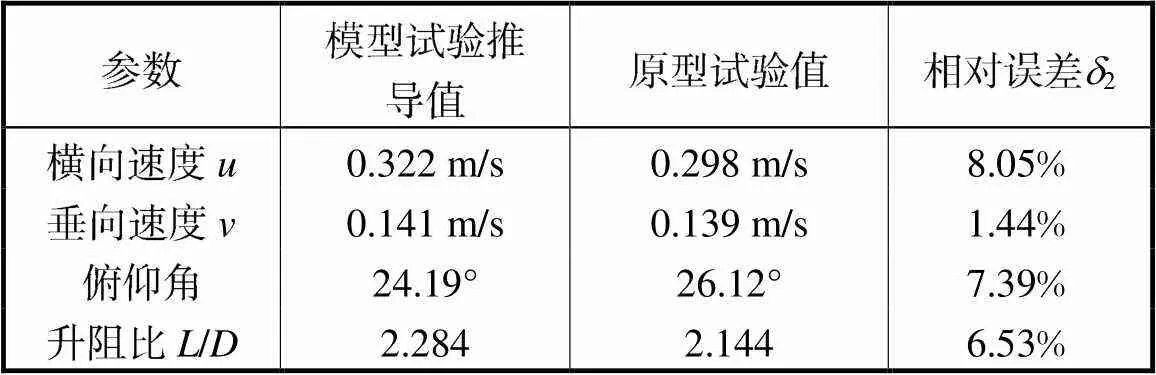
Tab.4　　Comparison of results between scaled model tests and PetrelⅡ sea trials(steady downward gliding stage)

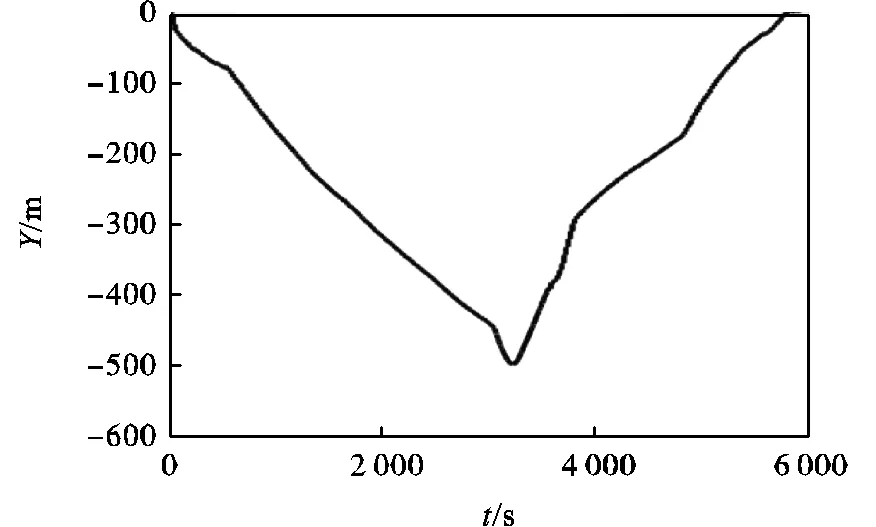
图10 垂直方向位移变化曲线

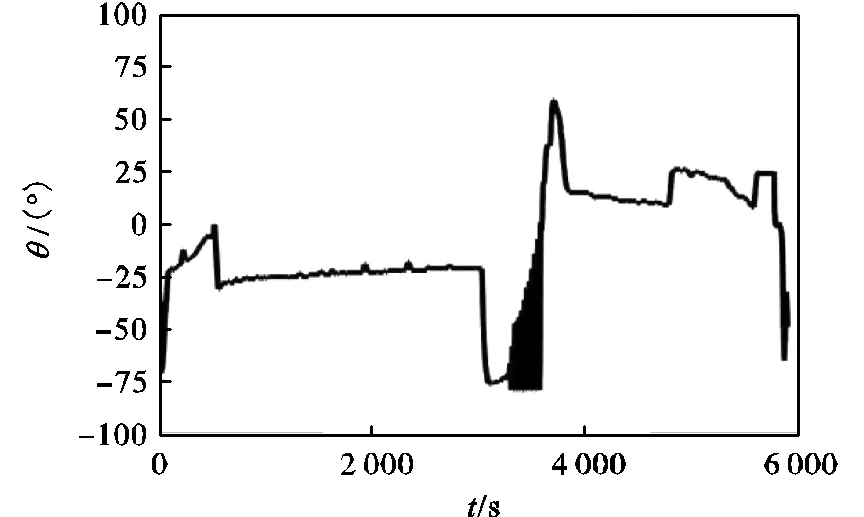
图11 俯仰角变化曲线

4 结 论

本文通过滑翔机动力学方程和周围流场N-S方程，利用相似理论推导了现象相似需要满足的相似准则，分析了各参数相似比和尺度相似比之间的关系，进一步分析了尺度效应对阻力系数的影响，设计了Petrel Ⅱ水下滑翔机缩比模型并进行水池试验，得到的主要结论如下．

(1) 若使水下滑翔机缩比模型和原尺度滑翔机完全相似，需要满足的相似准则为斯特劳哈尔准则、时均准则、马赫准则、弗劳德准则和雷诺准则，而在稳态滑翔状态下研究运动相似只需要满足弗劳德准则.

(2) 当尺度相似比大于0.5时，尺度效应对于水动力系数的影响较小，相对偏差在25%以下；当尺度相似比小于0.5时，尺度效应对水动力系数的影响更加明显．因此，以0.5为尺度相似比设计缩比模型最为合适．

(3) 0.5倍缩比模型在水池试验中得到的横向速度、垂向速度和升阻比与水下滑翔机原型海试结果的相对误差在10%以内，满足工程误差要求，即两者之间存在较好运动相似性．

(4) 0.5倍缩比模型和原型具有相同的滑翔经济性，由缩比模型的水池试验预报原型的滑翔经济性的方法切实可行．

［1］ Jenkins S A，Humphreys D E，Sherman J，et al，Alternatives for enhancement of transport economy in underwater gliders[C]//IEEE Proceedings of Oceans. San Diego，USA，2003：948-950.

［2］ Hess D E，Fu T C. Impact of flow control technologies on naval platforms[C]//AIAA Fluid Dynamics Conference and Exhibit. St Louis，USA，2003：256-259.

［3］ Hess D E，Fu T C，Cubbage S J，et al. Naval maneuvering research and the need for shear stress measurements (invited)[C]//AIAA Aerospace Sciences Meeting Including the New Horizons Forum and Aerospace Exposition. Orlando，USA，2010：321-323.

［4］ Crossland P，Nokes R C，Dunningham S，et al. A reconfigurable free running model capability for submarines with large/ratios[C]//Proceedings of Warship. Bath，UK，2014：114-118.

［5］ 刘 洋，肖昌润，杜佩佩. 潜艇自航模操纵性试验的模型设计[J]. 船海工程，2016，45(1)：6-12.

Liu Yang，Xiao Changrun，Du Peipei. Design of the self-propelled model for submarine maneuvering ability tests[J]. Ship & Ocean Engineering，2016，45(1)：6-12(in Chinese).

［6］ Berman S. Comparison of the lift，drag，and pitch moment coefficients of a slocum glider wind tunnel model with computational results by vehicle control technologies，inc[J]. IEEE Journal of Oceanic Engineering，2003，5(30)：25-29.

［7］ LaMothe P，Christian M，Brodsky P，et al. Preliminary exterior design and hydrodynamic evaluation of a small-scale underwater glider[C]//Oceans 2019. Seattle，USA，2019：356-367.

［8］ 王树新，宋 扬，王延辉，等. 基于Sobol’法的Petrel-Ⅱ水下滑翔机能耗参数灵敏度分析[J]. 天津大学学报(自然科学与工程技术版)，2017，50(2)：113-120.

Wang Shuxin，Song Yang，Wang Yanhui，et al. Sensi-tivity analysis of energy consumption parameters for Pet-rel-Ⅱunderwater glider based on Sobol’ method[J]. Journal of Tianjin University(Science and Technology)，2017，50(2)：113-120(in Chinese).

［9］ 施生达. 潜艇操纵性[M]. 北京：国防工业出版社，1995.

Shi Shengda. Submarine’s Maneuverability[M]. Bei-jing：National Defence Industry Press，1995(in Chinese).

［10］刘 方. 混合驱动水下滑翔机系统设计与运动行为研究[D]. 天津：天津大学，2014.

Liu Fang. System Design and Motion Behaviors Analysis of the Hybrid Underwater Glider[D]. Tianjin：Tianjin University，2014(in Chinese).

Motion Similarity of an Underwater Glider Based on Scaled Model

Liu Yuhong，Feng Dengxue，Deng Shihan，Liu Shuhe，Zhu Yaqiang

(School of Mechanical Engineering，Tianjin University，Tianjin 300350，China)

The similarity between two movements is the premise of predicting prototype movement characteristics and gliding economy using the scaled model of an underwater glider(UG). Taking the Petrel Ⅱ UG developed by Tianjin University as the research object，and starting from the similarity theory，the kinematic similarity criterion that the prototype and model of the UG should meet are deduced based on the dynamics and Navier-Stokes(N-S) equations. The computational fluid dynamics method is used to calculate the hydrodynamic coefficients of the UG at different scales，and the relationship between the scale similarity ratio and the lift as well as drag coefficients is obtained. Theoretical analysis shows that the Froude criterion is a necessary condition for the motion similarity of the UG prototype and its scaled model. In a certain scale range，the scale effect of lift coefficient and drag coefficient is not obvious，and it is most suitable to design the scale model with 0.5 as the scale similarity ratio. The Petrel Ⅱ UG scale model of the selected scale is tested in the pool，and motion parameters such as the speed and lift-drag ratio of the model at a certain pitch angle are obtained. The experimental results show that the motion similarity between the scaled model and its prototype is observed to exist. Results of the transverse velocity，vertical velocity and lift-drag ratio obtained from the scaled model in the tank tests are in good agreement with those of its prototype，obtained from the sea trials，and their relative errors meet the engineering error requirements. It is feasible to forecast the prototype motion parameters and gliding economy using the scaled model. The scaled model also provides a laboratory verification platform for the design of large UGs，which is of great significance to shorten the development cycle.

underwater glider；scaled model；similarity theory；motion similarity；gliding economy

10.11784/tdxbz202107017

N945

A

0493-2137(2023)02-0119-08

2021-07-07；

2021-10-25.

刘玉红（1971—  ），女，博士，教授.

刘玉红，yuhong_liu@tju.edu.cn.

国家重点研发计划资助项目(2019YFC0311701)；国家自然科学基金资助项目(51675372，51721003).

Supported by the National Key Research and Development Program of China(No. 2019YFC0311701)，the National Natural Science Foundation of China(No. 51675372，No. 51721003).

(责任编辑：王晓燕)