基于相序电流一致性的小电流接地故障方向算法

李玉敦，徐宪泽，孙孔明，范荣奇，梁正堂，薛永端

（1.国网山东省电力公司电力科学研究院，济南 250003；2.中国石油大学（华东）新能源学院，青岛 266580；3.国网山东省电力公司，济南 250000）

目前，小电流接地是我国配电网主要的接地方式，根据国家电网与南方电网的统计资料，为配电网供电的变电站一半以上采用中性点不接地方式，约1/3是谐振接地方式。过去我国电网运行规程允许配电网带接地故障运行一段时间，以避免用户停电，但极易引发两相接地短路，使故障扩大。因此，国家电网与南方电网均修改制定配电网运行规程，要求解决小电流接地故障的保护问题，快速就近隔离永久性接地故障，对小电流接地系统故障处理带来了新的挑战[1]。

针对小电流接地系统的单相接地故障，现场多利用暂态零序电压和电流实现故障检测，其中，暂态功率方向法[2-3]需要线路检测点安装零序电压互感器，不仅线路投资大，且零序电压互感器产生的接地点易成为系统的安全隐患。基于高频暂态电气量的暂态零序电流比较法[4]可以忽略消弧线圈的影响，但当发生高阻故障时暂态频率接近工频，滤除工频信号时可造成暂态信息的丢失。行波法[5]对装置采样频率要求极高，容易受到负荷投切等因素的影响，现场应用极少。

此外，近年来还有部分方法通过利用相电流、相电压实现故障检测，文献[6]通过分析故障后三相暂态电流突变量分布特征，提出衡量三相电流突变量波形的相似性识别故障区段的方法；文献[7]分析各相电流突变量及故障相电流频率分布特征，提出综合利用相电流突变量及重心频率的故障选线方法；文献[8]利用三相电流中的故障电流暂态分量的差异性实现故障定位。上述文献[6-8]均仅利用三相暂态电流突变量的差异性实现故障检测，并未深入、系统地分析故障后三相稳态电流突变量的分布特征，对故障后三相稳态电流突变量与零序电流间的关系未进行理论推导。文献[9]提出一种基于相电压电流突变量的频域定位算法，但该方法需要同时测量相电压及相电流突变量，而由于线路加装电压互感器成本较高，实际线路大多未安装电压互感器。

本文针对小电流接地系统，详细分析三相稳态电流突变量及零序电流分布特征，提出一种基于三相稳态电流突变量与3倍零序电流一致性关系指示接地故障方向的算法，可进一步确定故障线路和故障区段。该方法具有较高的适应性，对于不具备通信条件及未加装电压互感器的线路，可仅利用电流信息实现故障方向指示。

1 单相接地故障相电流突变量分布特征

由于配电线路较短[10-12]，忽略线路纵向阻抗，仅考虑线路对地零序电容，经简化后的配电网接地故障三相电流突变量分布网络如图1所示。图1中，配电系统共有若干条线路，其中，U̇f为故障点虚拟电源；Δİi_A、Δİi_B和 Δİi_C分别为第i条线路的A、B、C相电流突变量，i=1,2,…,n-1；Δİn_AP、Δİn_BP和Δİn_CP分别为第n条线路检测点P测得的A、B、C相电流突变量；Δİn_AQ、Δİn_BQ和 Δİn_CQ分别为第n条线路检测点Q测得的A、B、C相电流突变量；İf为故障点电流；Rf为故障点过渡电阻；LP为中性点消弧线圈；P、Q分别为位于第n条线路故障点上下游的检测点。开关K闭合时为谐振接地系统，开关K断开时为中性点不接地系统。

图1 配电网接地故障相电流突变量分布网络Fig.1 Distribution network of phase current fault component under grounding fault of distribution network

为了便于分析，将故障点到母线之间线路称为故障路径，健全线路、故障点下游线路及故障点上游的分支线路称为健全路径。

1.1 故障路径相电流突变量及零序电流分布特征

实际架空线路的不对称度为0.5%～1.5%，纯电缆线路的不对称度小于0.5%，因此可近似认为系统不对称度较小[13]，线路三相对地零序电容大小近似相等，线路对地零序电容为其各相对地零序电容的3倍。

小电流接地系统发生单相接地故障前后，系统线电压保持不变，线路的负荷电流不变[14-16]。因此，图1中故障路径检测点P处故障相电流突变量等于检测点P下游相对地零序电容电流与故障点电流之和，即

式中：C0n为故障线路各相对地零序电容；0为母线零序电压；k为检测点P后线路对地零序电容与本线路总对地零序电容之比，满足0＜k＜1；ω为工频角频率。

对于谐振接地系统，故障点电流为全系统对地零序电容电流与消弧线圈补偿电流之和，即

式中，C0Σ为系统全部线路对地零序电容。

设消弧线圈失谐度为v，可得在稳态条件下的消弧线圈感抗与系统对地容抗的关系为

将式（3）代入式（2）可得谐振接地系统的故障点电流为

将式（4）代入式（1），可得谐振接地系统故障路径检测点P处故障相电流突变量为

谐振接地系统故障路径检测点P处3倍零序电流可表示为

式中，0n_P为检测点P处零序电流。

对于中性点不接地系统，故障点电流为系统全部线路对地零序电容电流之和，即

将式（7）代入式（1），可得中性点不接地系统故障路径检测点P处故障相电流突变量为

中性点不接地系统故障路径检测点P处3倍零序电流可表示为

谐振接地系统及中性点不接地系统的故障路径检测点P处健全相电流突变量均为检测点P下游相对地零序电容电流，即

1.2 健全路径相电流突变量及零序电流分布特征

线路发生单相接地故障后，谐振接地系统及中性点不接地系统的故障点下游检测点Q处三相电流突变量分布规律相同，三相电流突变量均为该检测点下游相对地零序电容电流，即

式中，m为检测点Q后线路对地零序电容与本线路总对地零序电容之比，满足0＜m＜1。

谐振接地系统及中性点不接地系统检测点Q处3倍零序电流均为检测点Q下游线路对地零序电容电流，即

式中，0n_Q为检测点Q处零序电流。

健全线路各检测点测得的相电流突变量为检测点下游相对地零序电容电流，即

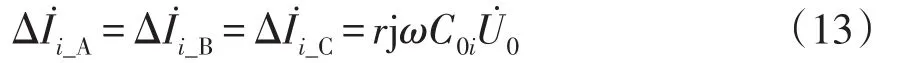
式中：r为第i条健全线路检测点下游线路对地零序电容与本线路总对地零序电容之比，满足0＜r＜1；C0i为第i条健全线路各相对地零序电容。

谐振接地系统及中性点不接地系统健全线路任一检测点3倍零序电流为检测点下游线路对地零序电容电流，即

式中，0i_r为第i条健全线路任一检测点零序电流。

2 基于相电流突变量与零序电流一致性的接地故障方向算法

2.1 接地故障方向判别原理分析

根据式（5）及式（10）可知，对于谐振接地系统，故障路径故障相电流突变量与健全相电流突变量之比满足的关系为

式中，x为系统全部线路对地零序电容与故障路径检测点下游线路相对地零序电容之比，满足x＞3。

由式（5）及式（6）可知，故障路径故障相电流突变量与3倍零序电流之比满足的关系为

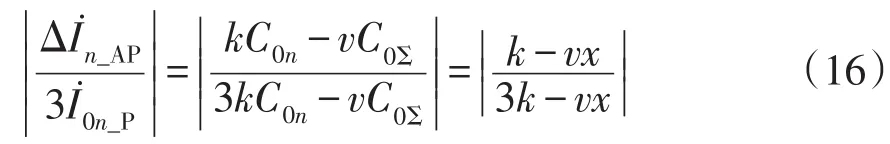
由式（6）及式（10）可知，故障路径健全相电流突变量与3倍零序电流之比满足的关系为

由式（15）、（16）可知，谐振接地系统中，故障路径故障相电流突变量与健全相电流突变量、3倍零序电流之比主要取决于消弧线圈失谐度v，同时也受系统全部线路对地零序电容与故障路径检测点下游线路相对地零序电容之比x，以及检测点后线路对地零序电容与本线路总对地零序电容之比k的影响。

我国绝大部分变电站采用预调式消弧线圈，而预调式消弧线圈多为调匝式消弧线圈。根据《国家电网公司变电运维通用管理规定（试行）》中消弧线圈检修细则规定，调匝式消弧线圈失谐度应调整在-5%～-20%之间。因此，当v=-5%、x=3、k=1时，式（15）有最小值为1.15；当x＞3且0＜k＜1时，式（15）满足的关系为

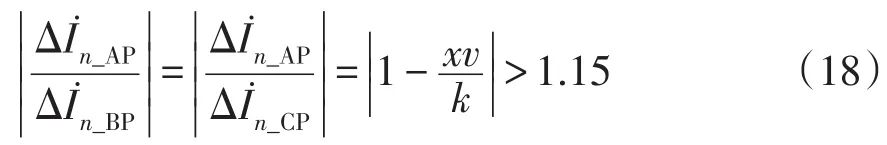
当v=-5%、x=3、k=1时，式（16）有最小值0.365；k=0时有最大值1，则式（16）满足的关系为

当v=-5%、x=3、k=1时，式（17）有最大值0.317，式（17）满足的关系为

同理，由式（8）及式（10）可得，在中性点不接地系统中，故障路径故障相电流突变量与健全相电流突变量之比满足的关系为

由式（8）及式（9）可知，故障路径故障相电流突变量与3倍零序电流之比满足的关系为

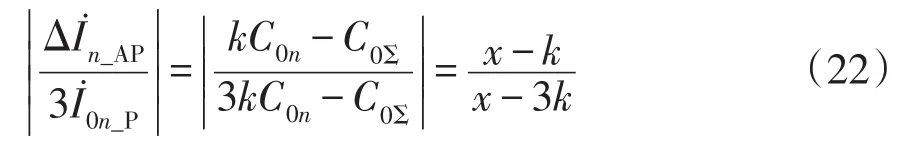
由式（9）及式（10）可知，故障路径健全相电流突变量与3倍零序电流之比满足的关系为

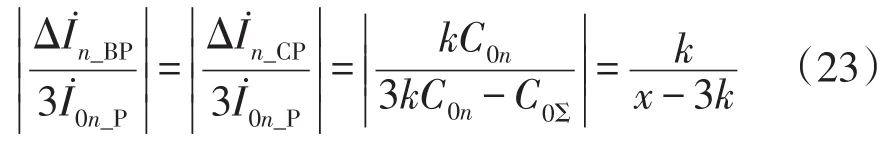
由式（21）可以看出，在中性点不接地系统中，故障路径故障相电流突变量与健全相电流突变量之比随x增大而增大，随k增大而减小；当x=3且k=1时，式（21）有最小值2，可得

当x=3、k=0时，式（22）有最小值1，可得

由式（11）～（14）可知，健全路径的三相电流突变量近似相等；三相电流突变量之比近似等于1；三相电流突变量与3倍零序电流之比相等，近似等于1/3。

基于第2.1节分析，可以发现，故障路径的三相电流突变量与3倍零序电流之比存在明显差异，谐振接地系统故障相电流突变量与3倍零序电流之比大于0.365，健全相电流突变量与3倍零序电流之比小于0.317，故障相电流突变量与健全相电流突变量之比大于1.15；不接地系统故障相电流突变量与3倍零序电流之比大于1，而健全相电流突变量与3倍零序电流之比远小于1，故障相电流突变量与健全相电流突变量之比大于2；健全路径的三相电流突变量相等，三相电流突变量与3倍零序电流之比一致，均近似为1/3。因此，可以利用故障路径和健全路径的三相电流突变量与零序电流的一致性关系判别故障点相对于检测点的位置。

2.2 整定原则

在小电流接地系统中，保护多采用零序电压启动[17]，本文所提方法能够用于未安装零序电压互感器的线路，线路检测点持续检测用于方向保护启动的3倍零序电流3I01，以此判断接地故障是否发生，启动门槛值的整定需要躲过线路不平衡电流。部分线路由于三相参数和长度不相同等原因产生不平衡电压[18-19]，该电压可表示为

式中：0_P为小电流接地系统不对称零序电压；u̇为不对称度，架空线路的不对称度一般为1.5%～2%，电缆线路的不对称度小于架空线路的不对称度[13]；d为补偿电网的阻尼率，中性点不接地系统一般为1.5%～2.0%，谐振接地系统一般为3%～4%[13]；v为消弧线圈失谐度，中性点不接地系统为1，谐振接地系统为-5%～-20%；为相电压幅值。

取极限情况，经计算可得不接地系统不对称零序电压最大为0P=-171.37∠1.14°V；谐振接地系统不对称零序电压最大为0P=-2 939.48∠149.04°V。考虑电缆线路不对称度很小，设定架空线路最长60 km时，零序电流可表示为

式中，0unb_i为第i条线路不平衡零序电流；C0为线路相对地零序电容。由式（28）可得不平衡零序电流最大为1.02 A。

设定方向保护启动门槛值Iset=1.1A，当线路检测点检测到3倍零序电流3I01超过Iset时，判断发生接地故障。

2.3 方向保护动作判据

定义检测点位于故障路径时故障方向为正，检测点位于健全路径时故障方向为负。设定故障稳态过程中三相电流突变量ΔIA、ΔIB、ΔIC中最大值ΔImax与三相电流突变量ΔIA、ΔIB、ΔIC中最小值ΔImin之比为T1；ΔImax与故障稳态过程中的3倍零序电流3I02之比为T2。

由于系统不平衡电流、负荷波动的影响，仅利用三相稳态电流突变量间的幅值关系或相似性关系容易引起保护误动，同时引入三相稳态电流突变量与零序电流的一致性关系作为综合判据可提高保护可靠性。考虑可靠性系数，根据式（18）～（20），谐振接地系统下的保护动作整定值Rset=1.2、Kset=0.37；根据式（24）～（26），中性点不接地系统下的保护动作整定值Rset=2.2、Kset=1.1。小电流接地系统方向保护动作综合判据可表示为

当满足式（29）时，判断故障方向为正，否则判断故障方向为负。

2.4 故障方向判别流程

故障方向判别具体流程如图2所示，具体步骤如下。

图2 故障方向判别流程Fig.2 Flow chart for judging the fault direction

步骤1线路中各检测点持续检测3倍零序电流3I01，若线路3倍零序电流3I01超过整定值Iset时，则判断系统发生接地故障，继续执行步骤2；否则，判断故障方向为负。

步骤2判定系统发生接地故障后，故障稳态过程中线路的检测点按照预设周期获取3倍零序电流3I02及三相电流突变量ΔIA、ΔIB和ΔIC，执行步骤3。

步骤3线路检测点计算得到故障稳态过程中三相电流突变量ΔIA、ΔIB和ΔIC中最大值ΔImax与最小值ΔImin之比T1；计算得到故障稳态过程中三相电流突变量ΔIA、ΔIB和ΔIC中最大值ΔImax与故障稳态过程中的3倍零序电流3I02之比T2，执行步骤4。

步骤4当谐振系统满足T1大于Rset=1.2且T2大于Kset=0.37时，判断故障方向为正，否则，判断故障方向为负；中性点不接地系统满足T1大于Rset=2.2且T2大于Kset=1.1时，判断故障方向为正，否则，判断故障方向为负。

3 仿真及现场试验验证

3.1 仿真验证

利用Matlab搭建10 kV小电流接地系统仿真模型如图3所示。由图3可知，该系统共有4条出线（L1～L4），其中，L1、L2、L3为架空-电缆混合线路，L4为纯电缆线路，线路具体参数如表1所示。线路L4上设置2个检测点，检测点P1、P2至母线间距离分别为2 km、6 km，故障点f1设置在距检测点P1的2 km位置；线路L1设置2个检测点，检测点P3、P4分别位于距母线3 km处及距母线5.4 km处；系统对地电容电流为52.18 A，消弧线圈失谐度-10%；开关K断开时为中性点不接地系统，开关K闭合时为谐振接地系统。各条线路末端统一采用1 MW恒阻抗负载。

表1 线路模型参数Tab.1 Line model parameters

图3 10 kV小电流接地系统仿真模型Fig.3 Simulation model of 10 kV small current grounding system

3.1.1 谐振接地系统

谐振接地系统三相电流突变量与零序电流波形如图4所示。图4中，ΔiA、ΔiB和ΔiC分别为A、B、C相电流突变量瞬时值；3i0为3倍零序电流。表2给出了谐振接地系统不同过渡电阻下仿真结果。

表2 谐振接地系统不同过渡电阻下仿真结果Tab.2 Simulation results of resonant grounding system under different transition resistances

图4 谐振接地系统三相电流突变量与零序电流波形Fig.4 Waveforms of three-phase current fault component and zero-sequence current in resonant grounding system

由图4及表2数据可知，当过渡电阻为100 Ω时，检测点P1、P2、P3和P4检测到3倍零序电流3I01＞1.1 A，检测点 P1、P2、P3和 P4均判断接地故障发生，但仅有检测点P1满足方向保护动作判据，指示故障方向为正；当过渡电阻为1 500 Ω和4 000 Ω时，检测点P1、P2、P3和P4检测到3倍零序电流3I01＞1.1 A，检测点 P1、P2、P3和 P4均判断接地故障发生，但仅有检测点P1满足方向保护动作判据，指示故障方向为正。

3.1.2 中性点不接地系统

中性点不接地系统三相电流突变量与零序电流波形如图5所示；表3给出了中性点不接地系统不同过渡电阻下仿真结果。

表3 中性点不接地系统不同过渡电阻下仿真结果Tab.3 Simulation results of neutral ungrounded system under different transition resistances

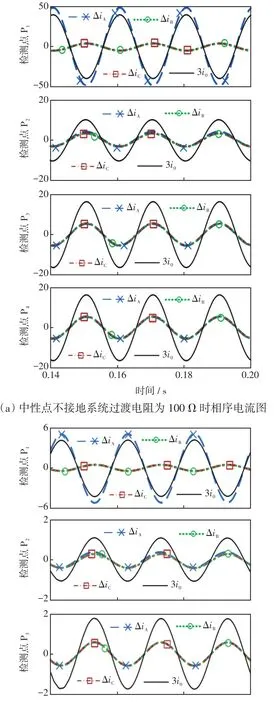
图5 中性点不接地系统三相电流突变量与零序电流波形Fig.5 Waveforms of three-phase current fault component and zero-sequence current of neutral ungrounded system

通过仿真中性点不接地系统f1处发生A相接地故障，此时仅有检测点P1位于故障路径，检测点P2、P3和P4均位于健全路径。由图5及表3可知，当过渡电阻为100 Ω时，检测点P1、P2、P3和P4检测到3倍零序电流3I01＞1.1 A，检测点P1、P2、P3和P4均判断接地故障发生，但仅有检测点P1满足方向保护动作判据，指示故障方向为正；当过渡电阻为1 500 Ω时，检测点P1、P3和P4检测到3倍零序电流3I01＞1.1 A，检测点P1、P3和P4判断接地故障发生，但仅有检测点P1满足方向保护动作判据，指示故障方向为正；当过渡电阻为4 000 Ω时，仅有检测点P1检测到3倍零序电流3I01＞1.1 A，判断接地故障发生，且满足方向保护动作判据，指示故障方向为正。仿真结果验证了本文方法的可行性。

3.2 现场试验验证

在HN省LH市某10 kV配电系统进行人工接地实验，所在的母线共有6条出线，系统对地电容电流约为124 A，消弧线圈失谐度调整为-10%。进行金属性接地实验并分别经100 Ω电阻、100 Ω电阻+球隙、500 Ω电阻、2 000 Ω电阻、草地等介质接地进行多次实验。选择经500 Ω电阻人工接地的实验结果验证本文所提故障方向算法的有效性，故障路径和健全路径三相电流突变量、零序电流实验波形如图6所示；数据如表4所示。

表4 现场试验数据Tab.4 Field test data

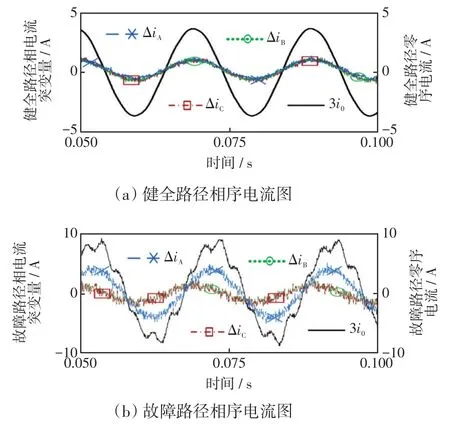
图6 故障点经500 Ω电阻接地的人工接地试验波形Fig.6 Artificial grounding test waveforms at fault point grounded by 500 Ω resistance

由图6可知，健全路径三相电流突变量近似相等，而故障路径中故障相电流突变量明显大于健全相电流突变量。由表4可知，健全路径三相电流突变量与3倍零序电流之比均为0.3，且三相电流突变量最大值ΔImax与最小值ΔImin之比为1.01，不满足本文第2.3节所提方向保护动作判据，判定故障方向为负，保护不动作；故障路径三相电流突变量与3倍零序电流之比分别为0.48、0.21、0.21，三相电流突变量最大值ΔImax与最小值ΔImin之比为2.3，满足方向保护动作判据，判定故障方向为正，保护经延时或交换信息后动作。根据上述分析，可以验证本文所提方法的正确性。

4 结语

本文通过详细分析小电流接地系统发生单相接地故障后，故障路径（故障点到母线之间线路）及健全路径（包含健全线路、故障点下游线路及故障点上游的分支线路）三相稳态电流突变量与零序电流分布特征可知，健全路径三相电流突变量近似相等，三相电流突变量与3倍零序电流之比基本一致；而故障路径故障相电流突变量大于健全相电流突变量，故障相电流突变量、健全相电流突变量与3倍零序电流之比存在明显差异。据此可以实现故障方向检测，仿真与现场实验数据验证了方法的正确性。

本方法无需在线路上附加一次设备，仅利用电流信息即可指示故障方向，对于未安装电压互感器的线路仍能可靠动作。高阻故障时能够避免电流互感器的测量死区，通过利用三相稳态电流突变量可提升抗共模干扰能力，各检测点之间可不依赖于通信，通过延时配合能够做到利用就地信息实现多级保护。