电流型有源消弧法性能分析与改进

赵国军，陈坤燚，李 沁，曾 伟，柯贤旺

（湖北民族大学智能科学与工程学院，恩施 445000）

随着配电网规模的不断扩大和电力电子设备及电缆线路的大量应用，导致谐振接地系统发生单相接地故障时故障点残流较大，电弧难以熄灭[1-2]。

因此，国内外学者针对配电网单相接地故障消弧问题，提出了诸多消弧方法，从原理上看主要包括无源消弧法和有源消弧法两类。无源消弧法主要包括消弧线圈和接地故障转移消弧装置（消弧柜）两类[3]。消弧线圈分为预调式消弧线圈和随调式消弧线圈，但无论何种消弧线圈都只能补偿电流的基波分量，对其有功分量和谐波分量无能为力，消弧效果具有局限性[4]。故障转移消弧装置采用断路器将故障相母线接地，从而旁路故障点，实现接地故障转移，钳制故障相电压，阻止故障电弧重燃。该方法受接地故障电流谐波分量和有功分量影响小，但是在重载、小过渡电阻的情况下可能出现不能转移故障点电流的情况，甚至有增大故障点电流的可能[5]。有源消弧法按照控制对象的不同，可以将其分为电流型和电压型两类。电流型有源消弧法通过控制接地故障点电流为0，促进电弧熄灭。电压型有源消弧法通过控制故障相电压为0，限制故障点恢复电压，从而达到消弧的目的。现有电流型有源消弧法，可以补偿接地故障的有功、无功功率和谐波电流，但补偿效果受对地参数测量精度的影响[6-8]。为此，文献[9-10]提出在故障前向配电网中注入电流，得到相应电压来计算对地参数，并代入零序电流计算公式，从而得到注入电流，实现消弧；文献[11]不需要单独计算对地参数，直接采用二次注入特定电流的方法得到注入电流的参考值，通过逆变器将参考电流注入配电网中性点，抑制故障点电压和电流至零，实现消弧。然而，上述测量方法均是在故障前完成参数测量，若故障中配电网存在线路结构上的变化（线路跳闸或检修），则很难保证消弧的可靠性。为此，文献[12]对文献[11]提出方法作了改进，利用FTU等配电网自动化设备，实时测量故障各装置安装处的零序电流及母线零序电压，从而实现配电网零序导纳的时候实时测量。此方法需借助于FTU，而并非所有配电网都配置了FTU，此方法的实施成本较高。文献[13-15]采用电压型有源消弧法，该方法以故障相电压为0作为控制目标，实现了消弧，无需测量对地参数。但是，此方法受负荷影响严重，在重载长馈线近末端发生小过渡电阻故障时会出现故障点残余电流增大，难以消弧的情况[16-18]。文献[18]通过过渡电阻的大小作为判据来选择电流型有源消弧法或电压型有源消弧法的方式实现消弧。此类通过切换模式实现消弧的方法，解决了电压型有源消弧法受过渡电阻、负荷的影响不能消弧的问题，然而对于电流型有源消弧法是否受过渡电阻、负荷、故障距离等因素的影响尚缺乏理论研究。此外，对地电容测量误差对故障点残余电流的影响也未见分析。

本文采用计及线路阻抗、负荷阻抗的模型，对故障点残余电流进行了分析，结果表明，在馈线末端重载、小过渡电阻情况下，对地电容测量误差为正误差时，会导致消弧困难；而一定的负误差，反而有利于消弧。此外，配电网注入零序电流改变相位与改变幅值比较，改变相位对故障点残流的变化率影响最大。基于上述结论，为适应配电网线路结构变化和计及线路末端小过渡电阻重载两种情况下的可靠消弧，提出了改进型有源电流消弧法。该方法在故障后动态调整零序注入电流，故障后首先从中性点注入幅值为90%的配网总电容电流，以保证注入电流的负误差，再通过调整注入电流的相位，引起故障残流的变化，从而计算出准确的注入电流，最后，改变注入电流相量，实现可靠消弧。

1 电流型注入消弧法性能分析

电流型注入消弧法的基本原理是：通过有源逆变器向配电网中性点注入零序电流，使故障点电流为0，从而实现消弧。消弧性能主要取决于注入电流的计算，传统电流型有源消弧法注入零序电流的计算公式[8-10，19]为

式中：C为故障相电压；ZC为对地零序阻抗；，R为对地泄漏电阻，C为对地电容。

式（1）是基于简化模型推导而得，只考虑了配电网对地电容和对地泄露电阻的影响，诸如故障距离、线路压降以及负载等参数均未考虑，存在较大误差。鉴于此，采用考虑线路阻抗、负荷阻抗的模型，并利用对称分量法对电流型注入消弧法的性能进行研究。

图1所示为带有电流型注入消弧装置的配电网。假设馈线L6发生单相（C相）接地故障，根据对称分量法可得如图2所示的复合序网。

图1 配电网消弧示意Fig.1 Schematic of arc-suppression of distribution network

图2 配电网单相接地故障复合序网Fig.2 Compound-sequence network of distribution network under single-phase grounding fault

图2中：为配电网正序电源；ZS为母线到电源之间的正序（负序）等效阻抗；Z为所有非故障线路及其末端负载的正序（负序）阻抗并联的等效阻抗；α为故障距离；ZL为故障线路正序（负序）等效阻抗；Zload为故障线路末端负载正序（负序）等效阻抗；ZL0为故障线路零序阻抗；Z0为系统等效零序阻抗；Rf为过渡电阻；f为故障点电流；0为逆变器等效电流源。

根据图2所示的复合序网可求得故障点电流f的表达式为

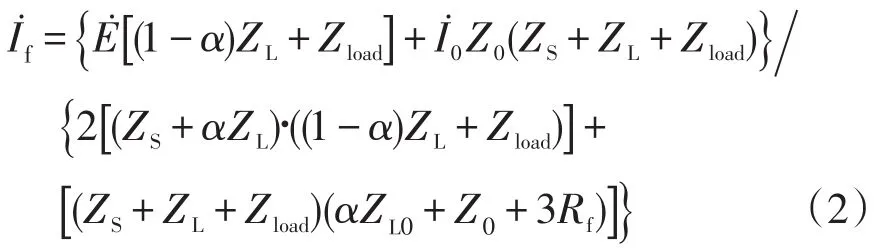
式中ZS较小，可忽略不计。因此，式（2）可近似表达为

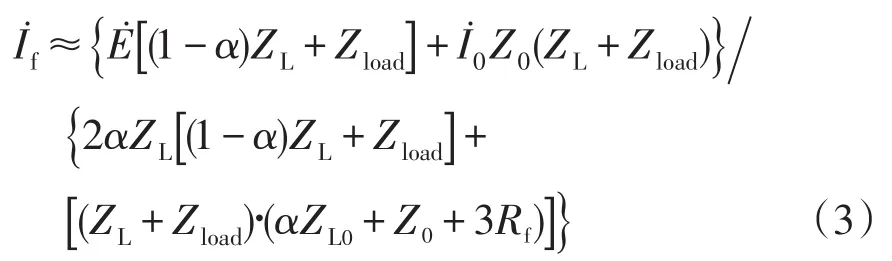
由图3可知：对地电容测量误差会增大残流。若要求残流低于5 A[12，18]，故障距离为0时，可容许的对地电容测量误差为-19.8%～16.3%；故障距离为0.5时，可容许的对地电容测量误差为-22.4%～10.6%；故障距离为1时，基本不能允许正误差。可见，在非首端故障时，对测量对地电容的负误差容忍范围更大，即，适当出现负误差对消弧更有利。

由式（3）可知：故障点残流f主要与注入电流0、故障距离α、故障线路负载阻抗Zload以及过渡电阻Rf有关。其中，0由式（1）计算得到，对地电容C的测量误差将会影响0，从而导致残流增大，难以可靠消弧。然而，式（3）较复杂，通过解析法很难分析故障点残流与各影响参数之间的关系，因此，可通过数值分析的方式展开研究。

1）故障距离α对残流f的影响

配电网各阻抗参数按表1选取，故障距离α在0～1范围内变化，对地电容误差在-100%～100%范围内变化，注入电流按式（1）计算。根据式（3）可得到残流f的变化规律，如图3所示。

表1 配电网阻抗Tab.1 Impedance of distributed network Ω

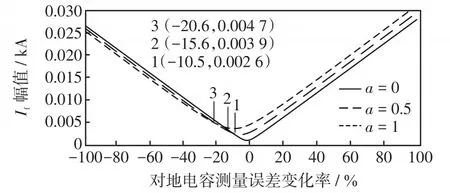
图3 故障距离的影响Fig.3 Influence of fault distance

2）过渡电阻Rf对残流f的影响

配电网各阻抗参数按表1选取，其中故障距离α为1，过渡电阻Rf在0.1～300 Ω范围内变化，对地电容误差在-100%～100%范围内变化，注入电流按式（1）计算。根据式（3）可得到f受Rf影响的变化规律，如图4所示。

图4 过渡电阻的影响Fig.4 Effect of transition resistance

由图4可知：残流低于5 A时，对地电容测量误差可容忍范围随过渡电阻增大而增加。此外，在线路末端小过渡电阻情况下，对地电容测量误差的容忍范围最小。若要求过渡电阻Rf在0.1～300 Ω变化，残流小于5 A，则可容许的对地电容的测量误差为-18.7%～0范围时，更有利于电弧熄灭。

配电网各阻抗参数按表1选取，其中故障距离α为1，过渡电阻Rf为0.1 Ω，负载阻抗Zload在25～311 Ω范围内变化，注入电流按式（1）计算。残流f随负载阻抗Zload的变化规律，如图5所示。

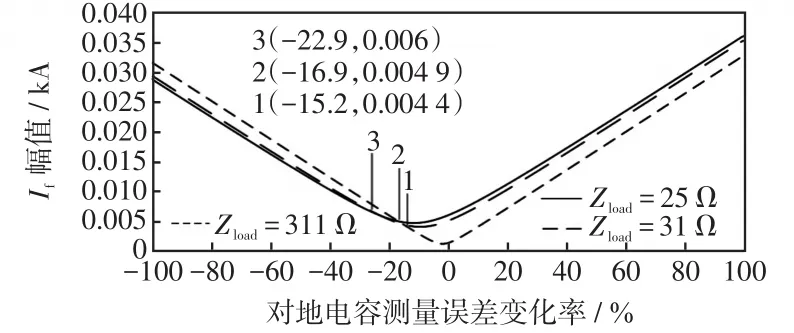
图5 负载阻抗的影响Fig.5 Influence of load impedance

由图5可知：残流低于5 A时，对地电容测量误差可容忍范围随负载阻抗的增大（负载容量减小）而增加。若要满足负载阻抗在较小值时，残流低于5 A，对地电容的测量误差需在负误差为-17%～-6.1%范围，才能满足消弧要求。

综上所述，配电网发生单相接地故障时，在过渡电阻、故障距离、负载阻抗的共同作用下，将迫使对地电容测量误差在负的情况下，使消弧效果更为显著。在线路末端小过渡电阻、重载（负载阻抗较小）情况下，注入电流计算公式按对地电容测量在负误差为-17%～-6.1%范围进行计算后，注入配电网，可使故障点电流接近零残流。

为此，在考虑了参数C、α、Zload以及Rf的变化对f0的影响，为适应配电网线路结构变化和计及线路末端小过渡电阻重载两种情况下的可靠消弧，本文将在现有电流消弧注入法的基础上提出一种新的方法，从而实现可靠消弧。

2 电流消弧方法改进

式（3）故障点电流与中性点注入零序电流的关系表达式为

令式（4）中的故障点电流f=0，则中性点注入零序电流的表达式为

将式（5）和 式（6）代入式（7），可得

式（8）可进一步化简为

由式（9）可知，逆变器向配电网中性点注入零序电流的计算公式不仅和、Z0有关，还与ZL、Zload有关。其中，故障距离α为0时，注入电流I0无需考虑ZL和Zload。若故障距离α不为0时，式（9）与式（1）比较，式（1）计算的注入电流是偏大的，阻抗偏小，即，其中。若要使|Z|更加接近于准确值，则可使对地电容C适当出现负误差C-(C-＜C)，即|ZC-|＞|Z|。可见，对地电容测量值为正误差时，按照式（1）计算注入电流会偏大，从而导致消弧困难；若对地电容测量值存在一定的负误差，则注入电流偏离真实值的差值偏小，因此，有利于消弧。为此，本文提出一种动态调整零序电流的方法，来实现式（9）注入电流的计算，完成可靠消弧。

配电网发生单相接地故障时，通过逆变器向中性点注入两次不同的零序电流，分别在故障线路首端测量其注入后的电流。其中，故障点电流。将和代入式（4），可知

进而可得

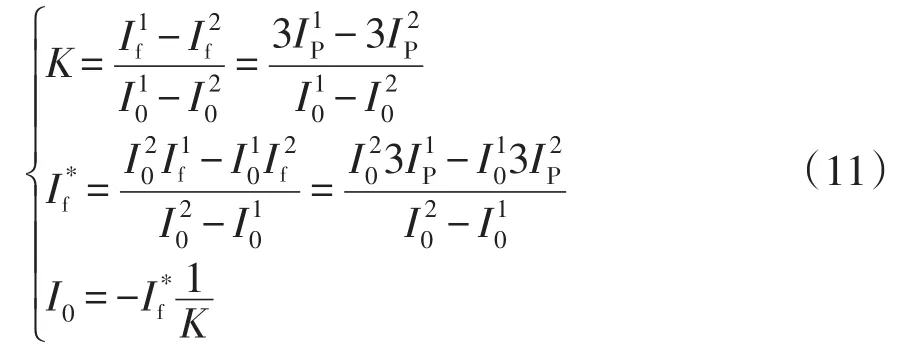
在计及故障距离、线路阻抗和负载阻抗时，动态调整二次注入零序电流，将其按式（10）～式（11）的方式计算最终注入电流，以此实现可靠消弧。此外，在动态调整注入电流时，可能会增大故障点电流。因此，还需考虑二次注入零序电流的大小。

配电网正常运行时，通过文献[11]注入法测量配电网对地电容参数。若发生单相接地故障，则第一次注入电流以正常情况下所测得的对地电容参数在负误差为-17%～-6.1%范围内进行动态调整注入；为保证第二次注入电流使故障点电流呈下降趋势，需考虑注入电流幅值和相位的选择问题。因此，下面将以第一次注入电流为基准进行数值变化，注入配电网中，观察故障点电流变化规律。

假设配电网C相发生单相接地故障，故障距离α为1，过渡电阻为100 Ω，其他参数如表1所示。其中，第1次注入电流按0.010 3∠60°kA给定。图6为第1次注入零序电流相位不变，幅值改变后的故障点电流变化情况；图7为第1次注入零序电流幅值不变，相位改变后的故障点电流变化情况。

图6 注入电流幅值变化对故障点电流的影响Fig.6 Influence of change in injection current amplitude on current at fault point

图7 注入电流相位变化对故障点电流的影响Fig.7 Influence of phase change of injection current on current at fault point

由图6可知，注入电流相位不变、幅值在原有数值的基础上变化时，故障点电流与注入电流的平均斜率约为-1.732 3，即注入电流每变化1 A，故障点电流变化1.7 A。由图还可知，在第一次注入电流幅值的基础上，相位不变、减少电流的幅值，可使故障点电流略微下降。由图7可知，注入电流幅值不变、相位在原有数值的基础上变化时，故障点电流与注入电流的平均斜率约为-24，即注入电流每变化1 rad，故障点电流变化24 A。由图7还可知，在第一次注入电流相位的基础上，幅值不变、减少电流的相位，可使故障点电流下降。此外，电流相位的取值范围较宽。

由图6和图7可知，第2次注入零序电流在第1次注入零序电流的基础上，只改变相位，不改变幅值进行注入，可以不用考虑逆变器调制比过调、输出电流控制精度问题，只需控制开关管开通关断时间即可实现相位角的变化，有利于在第2次注入零序电流就能实现可靠快速消弧的目标。

根据上述分析，本文对现有电流型有源消弧算法进行了改进，工作流程如图8所示。

图8 电流消弧法流程Fig.8 Flow chart of current arc-suppression method

配电网正常运行时，通过文献[11]注入法测量配电网对地电容参数。若发生单相接地故障，则第1次注入电流以正常情况下所测得的对地电容参数在负误差为-10%进行调整注入；如果电弧未熄，则在第1次注入电流的基础上减小其相位角后，进行第2次注入电流；若电弧未熄，则通过故障后2次注入的电流按照式（10）和式（11）计算注入电流，将该电流注入中性点，使故障点电流为0，电弧熄灭，实现可靠消弧。

3 仿真分析

为验证所提电流型有源消弧改进方法的有效性，本文通过PSCAD/EMTDC仿真软件建立如图1所示的配电网模型。配电网参数：电源电压为35 kV，阻抗为：（0.512+j2.3267）Ω；主变压器绕组采用连接△/Y，变比为35 kV/10 kV，容量为30 MV·A，正序漏抗为0.04 p.u.，空载损耗为0.001 92 p.u.；负载采用降压变压器与馈线连接，降压变压器变比为10 kV/0.4 kV。其中，配电网线路阻抗参数如表2所示。

表2 配电网线路阻抗参数Tab.2 Impedance parameters of line in distribution network

1）消弧方法性能验证

假设配电网馈线首端和末端C相发生单相接地故障，其中，故障距离分别取0 km和10 km，负载重载有功功率为1 MW，无功功率为0.05 Mvar，负载轻载有功功率为0.4 MW，无功功率为0.1 Mvar。对地电容为5.42 μF（阻抗为587.44 Ω），故障相电压幅值为5.9555∠150°kA。第一次注入幅值为90%的配网总电容电流，即幅值0.009 1 kA，相位60°；第2次注入零序电流：幅值0.009 1 kA，相位52°；计算注入零序电流按式（9）和式（10）计算所取。参数变化对消弧的影响如表3所示。

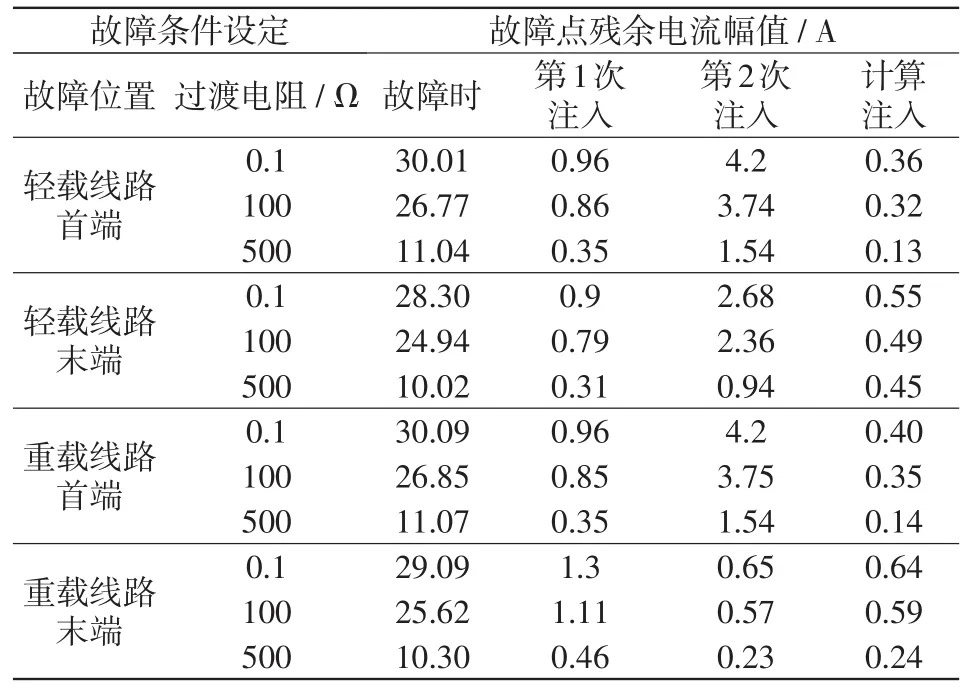
表3 参数变化对消弧的影响Tab.3 Influence of parameter variation on arcsuppression

由表3可知，配电网发生单相接地故障时，采用本文所提改进型有源电流消弧，可使故障点电流降至5 A以下，残流几乎为0 A，基本达到零残流消弧的目的，能实现可靠消弧。

2）与其他电流型有源消弧法比较

为验证所提消弧方法的可行性，本文和文献[10]、文献[11]进行了比较。仿真条件按照配电网线路结构变化和计及线路末端小过渡电阻重载（负载阻抗较小）2种情况下进行设置。假设配电网馈线首端或末端的C相发生单相接地故障，故障距离分别取0 km和10 km，过渡电阻取0.1 Ω和100 Ω，负载重载时有功功率为1 MW，无功功率为0.05 Mvar。其中，线路结构按馈线正常（对地参数阻抗587.44 Ω）和馈线断开（对地参数阻抗1145.89 Ω）来设置。消弧性能对比结果如表4所示。

表4 消弧方法性能比较Tab.4 Comparison of performance among arcsuppression methods

由表4可知，配电网线路结构不变（馈线正常）条件下，采用文献[10]电流型消弧法中的注入电流计算公式，注入电流后，故障点电流在重载线路末端小过渡电阻时，不能降至5 A以下。同样条件下，采用文献[11]中二次注入特定电流的方法得到注入电流的参考值，注入电流后，均能使故障点电流降至5 A以下，消弧效果较好。而本文所提消弧方法注入电流后不仅能使故障点电流降至5 A以下，还能使残流接近于0 A，基本达到了零残流消弧的目的。若配电网线路结构发生改变（馈线断开），文献[10]和文献[11]注入电流后，不能实现消弧。同样条件下，本文所提消弧方法可适应线路结构变化，可使故障点电流降至0 A附近，能实现可靠消弧。

通过上述仿真结果，验证了本文所提改进型电流消弧法的可行性，在配电网线路结构变化和计及线路末端小过渡电阻重载2种情况下均能实现可靠消弧，仿真结果与理论分析一致。

4 结语

传统注入电流计算公式未计及故障距离和负载阻抗，在重载馈线近末端发生小过渡电阻故障时，对地电容测量误差为正误差时，难以实现消弧；为负误差时，消弧效果较好。若线路结构改变，只有对地电容测量误差为负误差时，才能实现消弧。配电网注入零序电流改变相位与改变幅值相比，改变相位对故障点残流的变化率影响最大。为适应配电网线路结构变化和计及线路末端小过渡电阻重载2种情况下的可靠消弧，提出了改进型有源电流消弧法：故障后首先从中性点注入幅值为90%的配网总电容电流，以保证注入电流的负误差，再通过调整注入电流的相位，引起故障残流的变化，从而计算出准确的注入电流，最后，改变注入电流相量，实现可靠消弧。