基于高阶ESO的永磁直驱风电系统快速终端滑模控制

吴 影，高 林

（青岛科技大学自动化与电子工程学院，青岛 266000）

风能被认为是一种可再生的能源形式，因为它是太阳能活动的结果。利用风力发电能够妥善解决环境污染问题，节约化石燃料等不可再生能源，风力发电也逐渐成为我国发电领域的主力军。但由于风速具有易变性，随机性和不可预知等特点会使系统对风能的利用效率降低，如何最大程度地利用风能，降低风速变化对系统带来的负面影响，提高系统的鲁棒性，是研究风电系统最大功率跟踪MPPT（maximum power point tracking）控制的意义[1-2]。

风电机组主要的控制策略切换在额定风速点，分为额定风速以下的定桨变速风能的最大追踪运行和额定风速以上的变桨控制恒功率运行，本文主要的研究内容是额定风速以下的定桨变速风能的最大功率跟踪运行。实现最大功率跟踪的常用方法有反馈法，如最大功率曲线法[3]等，但实际中对机械功率的测量难以精确测量，使得控制精度降低。直驱式永磁同步发电系统中[4-5]永磁同步发电机转子的磁极对数很大，可以直接与风力机的轮毂相连，取消了齿轮箱的增速机构，减少了齿轮箱维护费用，而且采用变速恒频的风力发电技术[6-7]可以最大限度地提高对风能的转换率。轮毂直接与发电机转子连接，使风速变化给系统带来的外界扰动直接作用在发电机的转子上，增加了对发电机的控制难度。

鉴于此，越来越多的智能控制方法被应用在风力发电系统中，如：PI控制[8]、滑模变结构控制[9]、自适应控制[10]、自抗扰控制[11]等。但传统PI控制对转速的控制精度不高，易出现超调现象，很难消除外界扰动对系统带来的负面影响。文献[10]采用一种基于自适应模糊控制器和非线性扰动观测器的反馈线性化控制方法。通过自适应律动态调整模糊规则，改善模糊控制器的学习能力，增强系统的鲁棒性，但由于模糊控制所需参数众多，计算比较复杂；文献[11]利用非线性光滑函数代替非线性组合幂次函数，提出基于非线性扩张状态观测器的非线性抗扰控制方法，有效提高了系统的抗扰能力；文献[12]在文献[11]的基础上，又设计了非线性滑模趋近律，将NLEAO与非线性滑模控制率相结合，消除了传统滑模控制中的高频抖振现象；文献[13]设计了一种基于文献双曲正切的非线性跟踪微分器，该微分器函数形式简单，消除了输出抖振问题，但时变参数难以整定；文献[14]提出一种基于自适应观测器的滑模控制方法，通过自适应观测器估计发电机电动势和负载转矩，提高系统的响应速度，但在风速随机发生变化时，此方法对发电机转速的控制精度有所下降。

因此，针对系统的输入转矩受外界风速多变影响导致转速控制精度下降的问题，本文引入高阶扩张状态观测器HOESO（high-order extended state observer），利用扰动先验知识快速精确估计出系统的转矩和转速，比传统ESO的估计效果更佳。滑模控制算法具有响应速度快、鲁棒性强等特点，本文设计快速终端滑模控制器以HOESO的输出转速和转矩为输入信号，实时补偿掉由风速变化引起发电机转矩突变带来的影响，提高系统的转速响应能力，实现最大功率跟踪。本文将此方法应用在风电系统模型中，分别观察阵风、渐变风、随机风3种不同风速下发电机转速和转矩的跟踪效果，仿真结果表明基于高阶扩张状态观测器的快速终端滑模复合控制方法，不仅实现转速的无超调快速响应，而且控制精度高，系统鲁棒性强。

1 永磁直驱风力发电系统的数学模型

风力机获取风能后将其转化为机械能，通过转矩的形式输送到发电机并发出交流电，不完全稳定的交流通过机侧变流器整流为幅值稳定的直流电，直流电经网侧逆变器逆变成与电网幅值和频率一致的交流电，使机械能转化为电能输送到电网。本文主要研究发电机机侧变流器得转速外环控制部分，永磁直驱风力发电系统的基本结构如图1所示。

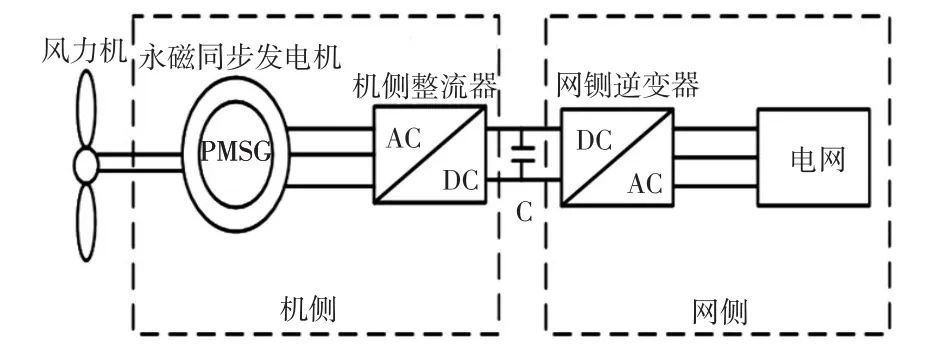
图1 永磁直驱风力发电系统基本结构Fig.1 Basic structure of permanent magnet direct-drive wind power generation system

1.1 风力机的数学模型

气流使叶片运动起来，将风能转化为机械能。由Betz风能理论可知，风力机转化的机械功率Pm可表示为

式中：ρ为空气密度，kg/m3；v为风速，m/s；r为风力机叶片的半径，m；Cp(λ,β)为风能利用系数；β为桨距角，（°）；λ为叶尖速比，可以表示为

式中，ωm为风力机的角速度，rad/s，由风速决定。

由式（1）可知风能利用系数由叶尖速比λ和桨距角β决定，可表示为

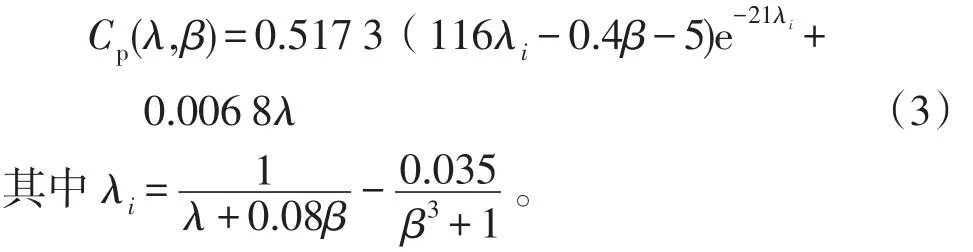
Cp(λ,β)的曲线如图2所示。由图2可知，当桨距角一定时，Cp(λ,β)随着λ的变化而变化，且存在一个最佳叶尖速比λopt使Cp(λ,β)达到最大值。由此可知，额定风速下最大功率跟踪是当风速发生变化时，通过调节转速，使风力机在不同风速下都能始终运行在最大风能利用系数点处，从而输出最大功率。因此如何控制系统的转速是研究风电系统最大功率跟踪控制的核心。

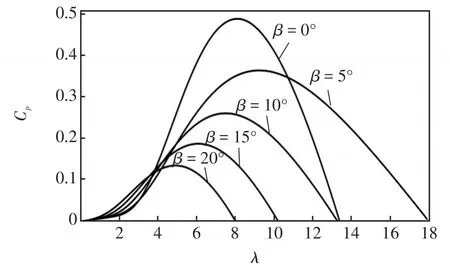
图2 风能系数曲线Fig.2 Curve of wind energy coefficient

风力机的气动转矩Tm与其捕获的机械功率满足

结合式（1）、式（2）和式（4）可得Tm为

1.2 PMSG的数学模型

隐极式永磁同步发电机d轴和q轴定子电感相等，在d-q旋转坐标轴下建立其数学模型，即

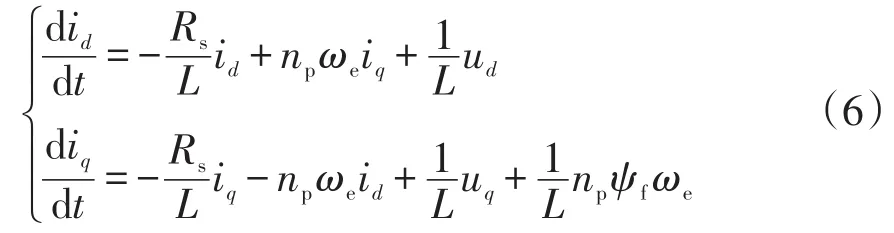
式中：id为d轴定子电流分量；iq为q轴定子电流分量；ud、uq分别为d轴和q轴的定子电压分量；Rs为发电机电枢电阻；L为定子电感；np为转子磁极对数；ψf为永磁体的磁链；ωe为发电子转子的转速。

发电机电磁转矩的表达式为

由式（7）可知，发电机的电磁转矩由iq决定。

永磁同步发电机不需要通过齿轮箱增速，风机通过传动链直接与发电机转子相连，所以ωe=ωm。则发电机传动系统处的机械运动方程为

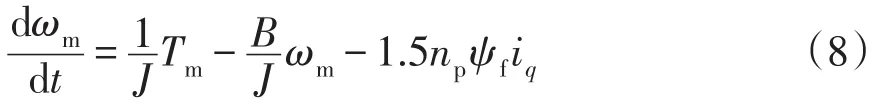
式中：J为发电机转动惯量；B为传动系统产生的摩擦系数。

2 快速终端滑模控制器

传统PI控制无法解决风电系统的非线性问题，因此本文设计快速终端滑模控制器，使转速外环的控制性能更加优越。

快速终端滑模控制器的设计如下。

设系统的状态变量为

系统的转速误差方程为

由式（10）可得

由式（8）可得

设计滑模面为

式中：α＞0，β＞0，0＜γ＜1。关于参数α、β和γ的选择方法详见文献[15]。

则有

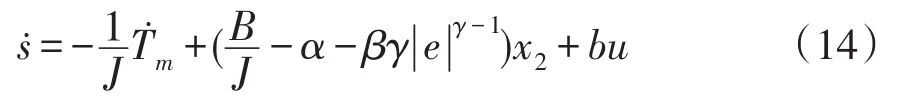
设滑模趋近率为

式中：k＞0，0＜α＜1。关于参数k和α的选择方法详见文献[16]。

由式（14）和式（15）可得控制律为

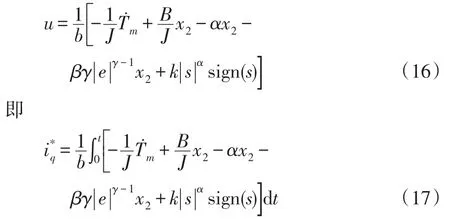
3 高阶扩张状态观测器

上文中提到将滑模控制应用在发电机的转速外环，忽略风力机的气动转矩对系统带来的未知扰动，本文引入高阶扩张状态观测器来对气动转矩进行精确估计，提高系统的鲁棒性。

高阶扩张状态观测器的设计如下。

令y=x1为系统的输出，则式（12）可表示为

设系统所受扰动为f(·)，可表示为

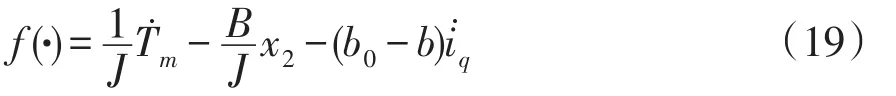
式中，b0为b的近似值。

扰动f(·)即系统所受的非线性摩擦力，内部参数变化，外界风速的不可控性给系统带来的扰动。当系统趋于稳定时，x2≈0，b0-b≈0，系统仅受外界干扰的影响。

式中：n＞0，m＞0。关于参数n和m的选择方法详见文献[17]。

定义系统的状态变量x3=f(·)，，。重新对系统进行构造，得

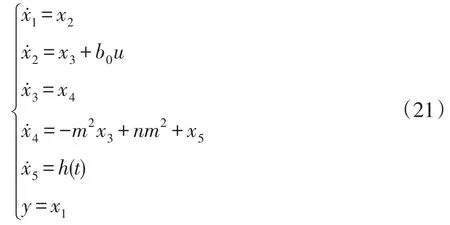
当系统进入稳态后，h(t)趋近于0。针对重构后的系统设计高阶ESO为

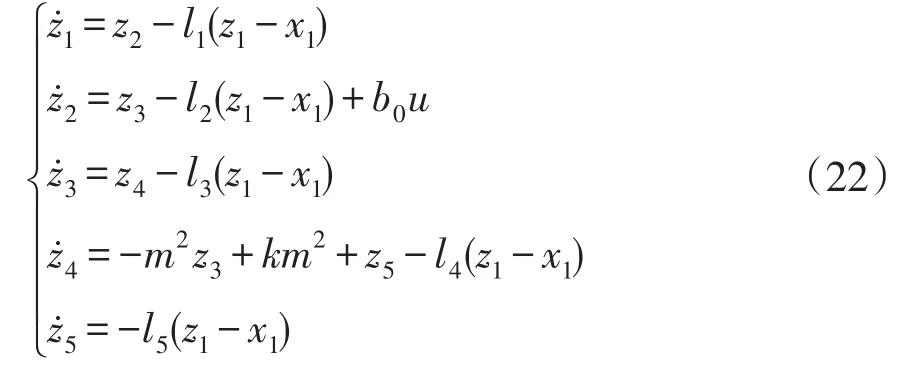
式中：l1、l2、l3、l4、l5为观测器误差增益参数，由观测器的带宽决定；z1～z5分别为x1～x5的观测值。

直驱式永磁同步风电系统是一个干扰性强的非线性系统，当系统受到随时间变化的外部扰动时，传统的扩张状态观测器不能准确观测出系统的转矩和转速。所以本文对系统进行重构，设计了高阶扩张观测器，在外界风速发生变化时，能够精确估计系统的实时转矩，实现系统转速在不同风速下都可以快速准确地跟踪上最佳转速，且不会降低系统的动态性能。

4 基于HOESO的快速终端滑模控制

4.1 复合控制的设计

结合广义扩张状态观测器，用观测器得出的估计值代替x1、x2、x3，则式（16）可写为

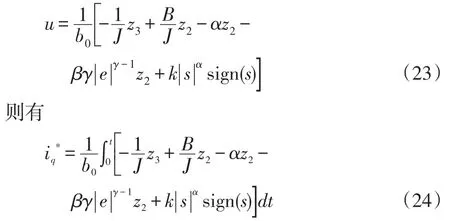
系统控制结构如图3所示。

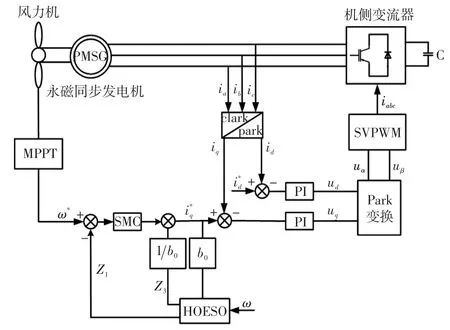
图3 控制结构Fig.3 Control structure

4.2 控制器稳定性分析

选取Lyapunov函数为

将式（23）代入式（14），得

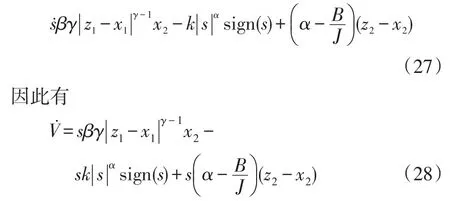
令|z1-x1|≤a1，(z2-x2)≤a2，其中a1、a2是常数，则

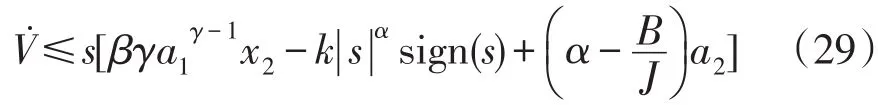
由式（29）可知，当s≠0时，满足不等式

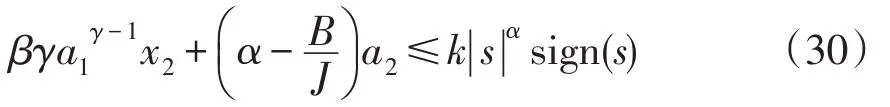
则=≤0 ；当s=0 时，==0。

5 仿真结果与分析

为验证本文所提控制方法的有效性，在MATLAB-Simulink仿真软件中建立风电系统模型，将本文设计的复合控制器应用到模型里，将自然界中的风速拆分为阵风、渐变风、自然风3种风速，并观察3种风速分别作用下的转速跟踪和转矩跟踪情况，并对比传统PI和滑模控制进行研究分析，风力发电系统主要的仿真参数如表1所示。

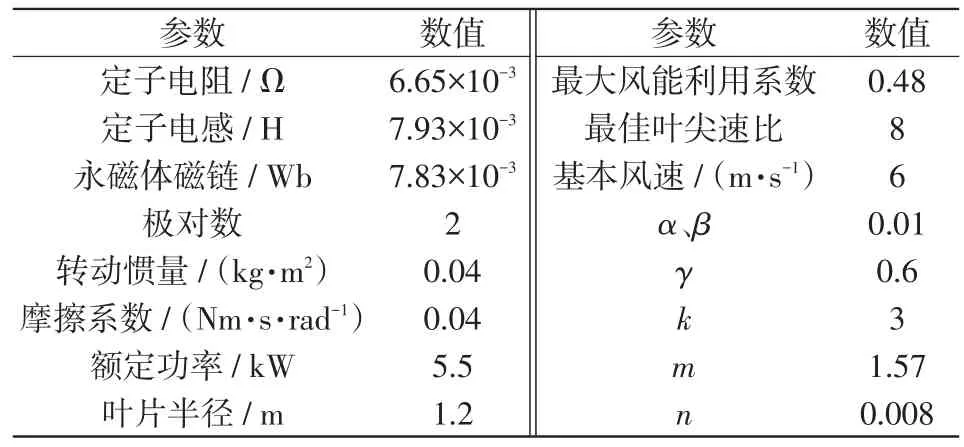
表1 风力发电系统主要参数Tab.1 Main parameters of wind power generation system

5.1 阵风仿真分析

阵风用来表达外界风速突然发生变化的情况，其数学模型为

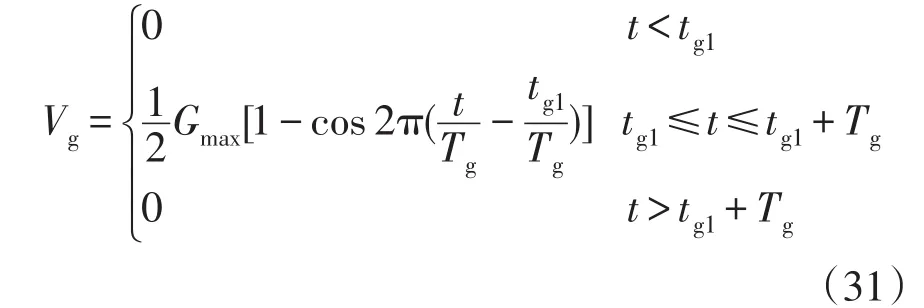
式中：t为时间；tg1为阵风开始时刻；tg1+Tg为阵风结束时刻，Tg为阵风周期；Gmax为阵风峰值。本文的参数取值为：Gmax=8 m/s，tg1=1 s，Tg=4 s。

阵风作用时系统的转速跟踪结果如图4所示。

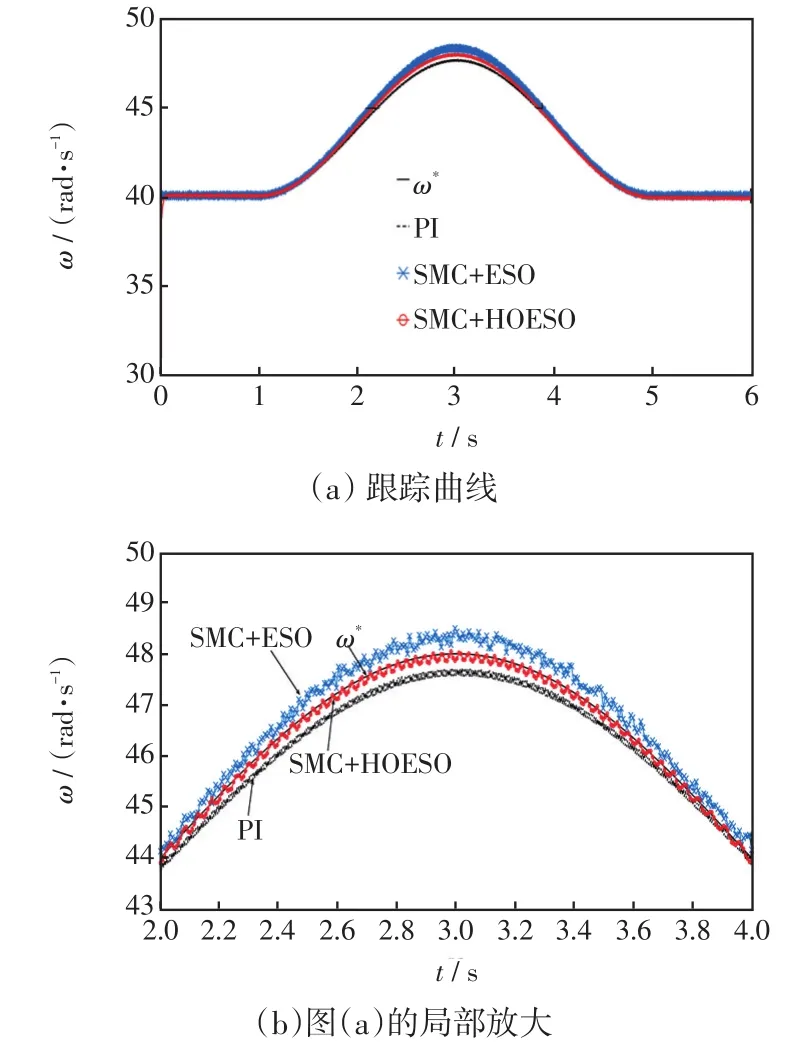
图4 阵风作用下发电机转速跟踪曲线Fig.4 Generator speed tracking curve under the effect of gusty wind

由图4可知，在阵风开始作用时（即1 s＜t＜5 s时），对比PI控制器和基于传统ESO的滑模控制器结合这两种控制算法，本文采用的SMC与HOESO结合的控制方法可以完全跟踪到系统给定的最佳转速ω*，且调节时间更短，控制精度更高。

5.2 渐变风仿真分析

渐变风用来表达风速逐渐变化的情况，其数学模型为

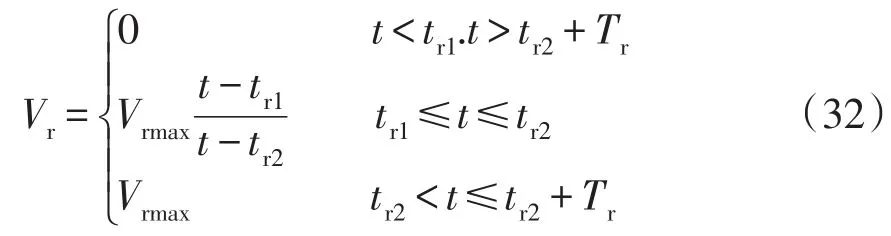
式中：Tr为渐变风存在的时间；tr1为渐变风开始时刻；tr2为渐变风结束时刻；Vrmax为渐变风峰值。本文的参数取值为：tr1=1s，tr2=3s，Tr=2s，Vrmax=8m/s。

渐变风作用时系统的转速跟踪曲线如图5所示。

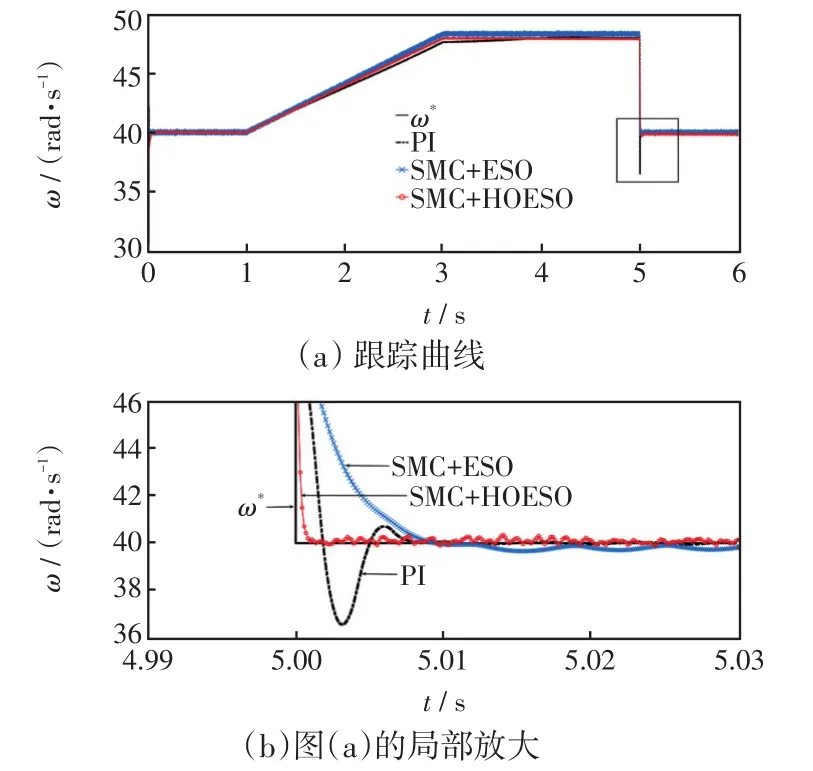
图5 渐变风作用下发电机转速跟踪曲线Fig.5 Generator speed tracking curve under the effect of gradual wind

由图5可知，当风速缓慢变化时(1 s＜t＜3 s)，本文设计的复合控制器比其他两种控制器对转速的控制性能更优秀；当风速在第5 s突然下降时，PI控制器对转速的控制有明显超调，基于传统ESO的滑模控制器对转速的响应时间超过0.01 s。本文提出的控制器可以控制转速在0.01 s内响应，调节速度快，能实现完全无超调。

5.3 随机风速仿真分析

本文用随机噪声风速来模拟随机风，表达风速高度变化的特性，其数学模型为

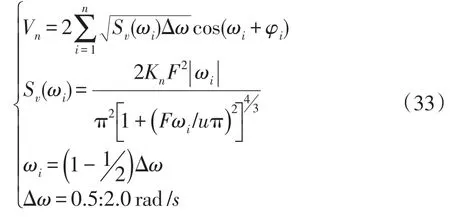
式中：Sv(ωi)为谱密度函数；ωi为第i个分量的角频率；Δω为随机分量的离散间距；φi为随机变量，均匀分布在[0 ,2π]；Kn为地表粗糙系数；F为扰动区间，m2；u为平均风速，m2/s；本文的参数取值为：Kn=0.004，F=2 000m2，n=50。

随机风作用时系统的转速跟踪曲线如图6所示。

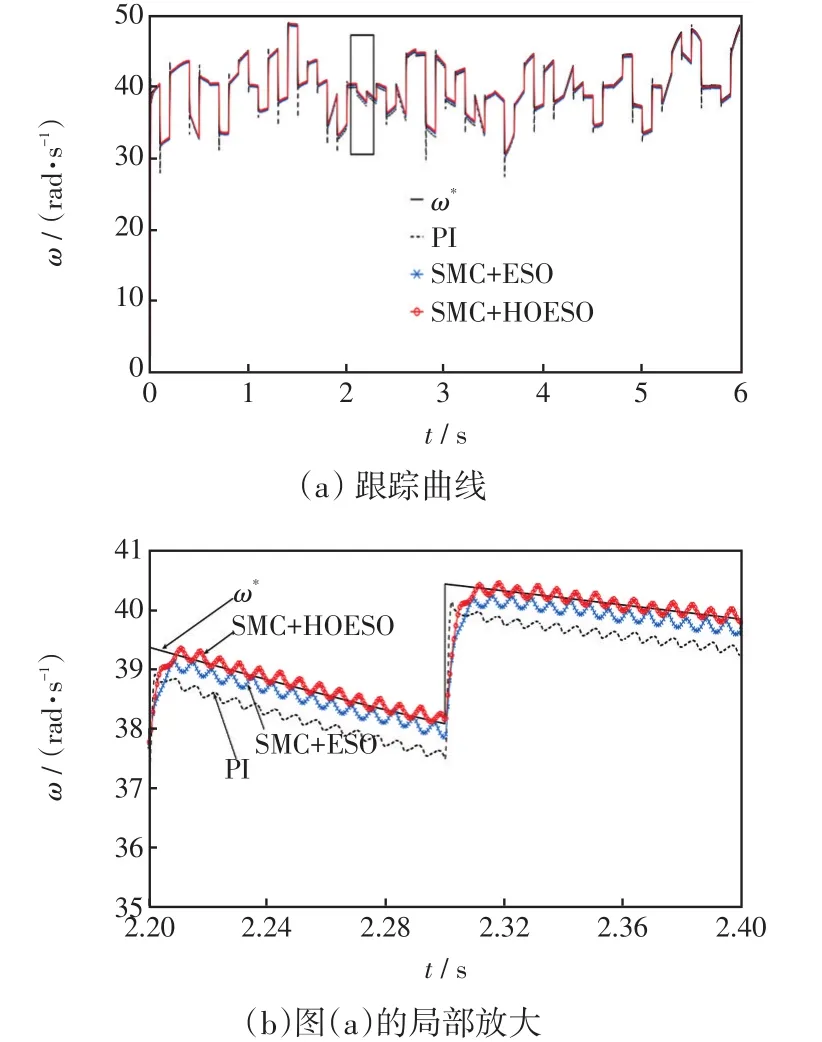
图6 随机风作用下发电机转速跟踪曲线Fig.6 Generator speed tracking curve under the effect of random wind

由图6可知，当风速随机变化时，PI控制器对转速的控制存在大约0.5 rad/s的误差，基于传统ESO的滑模控制器存在大约0.2 rad/s的误差，但本文设计的复合控制器能够快速精准跟踪系统的最佳转速。

由以上转速跟踪仿真结果表明，不管何种风速下，本文提出的复合控制方法效果都比其他两种控制器的效果更佳，该复合控制器可以实现完全无超调，对转速的控制更准确。

图7～图9是3种不同风速作用下的扰动误差观测曲线，从图9可以看出本文所设计的高阶ESO对系统转矩的响应时间在0.02 s内，且观测误差基本稳定在0，传统ESO的响应时间在0.06 s左右，且观测误差大，所以HOESO对转矩的跟踪性能比ESO的更好，受风速变化的影响更小。

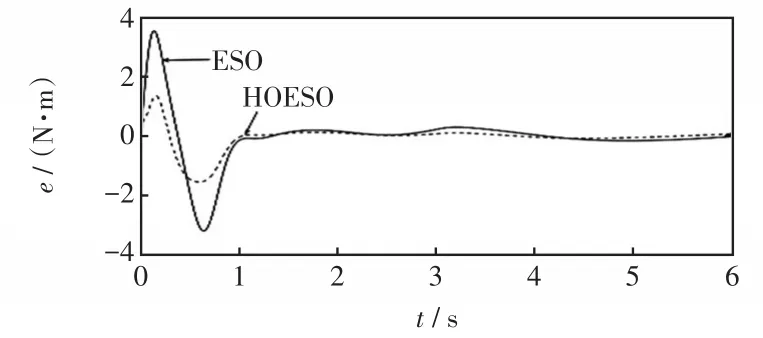
图7 阵风作用下的扰动误差曲线Fig.7 Disturbance error curve under the effect of gusty wind

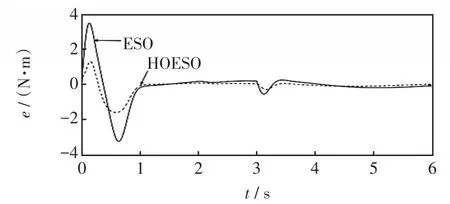
图8 渐变风作用下的扰动误差曲线Fig.8 Disturbance error curve under the effect of gradual wind

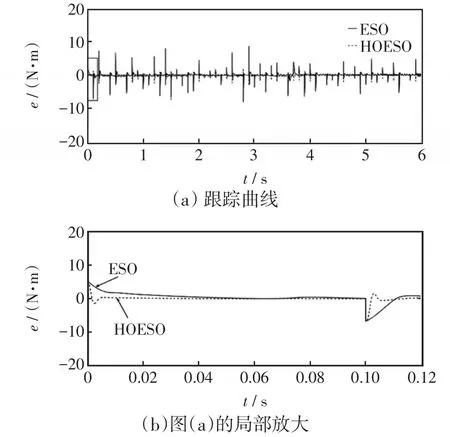
图9 随机风作用下扰动误差曲线Fig.9 Disturbance error curve under the effect of random wind

综上所述：对比传统PI控制和基于传统ESO的滑模控制，基于高阶扩张观测器的滑模控制器具备动态性能好，控制精度高，鲁棒性强的优势。

6 结语

本文在研究永磁直驱风力发电系统的最大功率跟踪的基础上，针对外部扰动的不确定性，提出了一种基于高阶扩张状态观测器的快速终端滑模复合控制方法。首先设计高阶扩张状态观测器，在风速易变的情况下，实现对系统转速和转速的准确估计，增强系统的稳定性，然后采用扰动补偿技术，前馈到快速终端滑模控制器中进行补偿，提高系统的响应速度。仿真结果表明，将高阶扩张状态观测器应用在风电系统的转速外环控制中，对系统的转矩和转速进行精确估计和主动补偿，提高系统的动态性能。尤其在风速突然发生变化时，对比传统PI和滑模控制方法，对转速的控制精度更高，受风速突变的影响更小。综上所述，无论风速如何变化，本文设计的复合控制方法，都可以使系统的转速快速响应，控制精度高，增强风力发电系统的鲁棒性，实现最大功率跟踪，提高发电效率。