基于子图同构的电力系统故障建模方法

李 鑫，刘佳钰，龚正宇，梁晓斌，汤 凡，张宇栋

（国家电网有限公司西南分部，成都 610041）

电力系统故障建模是利用电力系统仿真数据模拟系统常见故障以及故障后继电保护装置动作的数据工作。故障建模是构筑电力系统在线安全分析所依赖的故障集合的基础[1]。准确而全面地故障建模，能够提高离线电网计算分析的效率，更加客观科学地指导电网安全稳定运行[2]。

随着“碳达峰，碳中和”行动方案的提出[3]以及“双高”电网形态的不断演化[4]，相比于传统电力系统，新型电力系统仿真面临着元件数量、控制目标规模、故障形态与仿真场景复杂度加速上涨的趋势，这将极大地挑战电力系统在线及离线安全分析水平，其中故障建模又是影响电力系统安全性最直接的因素。当前电力生产中，故障建模主要由人工完成，存在如下局限性：

（1）在线安全分析中，故障集合无法根据系统日常检修等临时运行方式实时状态进行调整，容易误判电力系统安全状态，影响电网运行的安全性或经济性；

（2）电力系统诸多投退、改造等工程导致故障需要建模；

（3）涉及多个电网元件以及多套自动装置动作逻辑的复杂故障（如开关拒动等连锁故障），故障建模繁琐极易出错。

电力系统故障建模相关方法研究目前较少，原理主要分为2类：一类是半自动化方法，主要原理是对数据格式进行转换[5]；另一类研究基于图计算的故障建模方法，构建了一个基于图计算的故障建模统一架构[6]，算法效率极高，但缺点是需要针对每一类故障的数据结构特点进行独立算法开发，对特定仿真平台与数据管理习惯比较依赖，很难直接将已有的算法推广到其他仿真平台或有不同数据建模习惯的地区。

不同的仿真工具对电力系统有着不同的数据存储习惯，但其数据结构的本质是图，图论相关方法作为一种成熟的理论适合处理与电力系统网络拓扑有关的问题。电力网络作为一种重要的复杂网络得到充分的研究[7-10]，揭示了其“小世界”[7]且节点的度有幂率特征[8]，以及电力网络对无法承受针对关键节点的恶意攻击，但对于一般性的随机攻击具有一定的承受能力[9-10]的重要性质；以上研究着重于对网络一般性质的探索。而就网络结构本身方面，图论在电网断面分析[11-12]与挖掘[13]方面有比较成熟的应用；图论相关算法针对网络分区[14-15]、保护配合[16]、故障定位[17]及重构恢复[18-19]均有一些积极尝试。

作为图论应用[20]的一个重要方向，大量的计算机视觉、人工合成同构分子方面的应用需求促使了以VF3算法为代表的子图同构算法研究[21-23]不断推进。子图同构是在目标图（模式）中搜索给定子图（模式）的算法。本文基于图论相关概念[20]以及子图同构算法[21-23]，对电力系统故障建模问题进行了研究。首先提出了电力系统故障建模问题的数学表达，然后结合电力系统网络节点类型分布特点与节点语意信息，提出了基于子图同构的电力系统故障建模方法。最后通过一个规模较大的区域电网算例对本文方法进行了应用。

1 电力系统故障模型分析

1.1 图论基础

一个简单无向图G由节点集合V以及节点之间连接的边的集合E组成，记作

式中：V为图G所有的节点组成的集合；E⊂V×V为图G所有的边组成的集合，运算符号“×”表示集合的笛卡尔乘积运算。

d(v,G)表示节点v在图G中的度，即节点v邻居节点的数量，表示为

式中：nei(v,G)表示节点v的邻居节点集合，nei(v,G)={u|u∈V,(u,v)∈E}；运算符号“ ||”表示集合中元素的个数。

定义节点类型函数σ:V→C表示集合V中每个节点的类型ci∈C={c1,c2,…,cq}，即

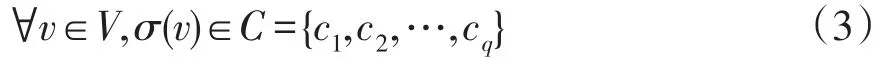
式中，q为节点类型的数量。

A(G)表示图G的邻接矩阵，即

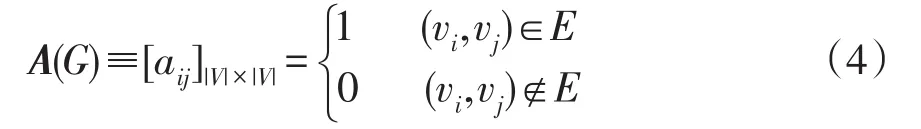
子图同构定义：给定2个简单无向图Gf=(Vf,Ef)与G0=(V0,E0)，如果存在一个单射函数λv:Vf→V0，满足条件

则称Gf与G0子图同构。由于Gf与G0均是简单图，在节点映射λv下，必然存在对应边的单射关系λe:Ef→E0，即

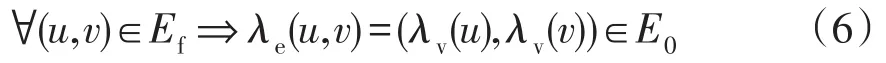
在节点映射λv下，定义节点对映射集合M⊂Vf×V0以及边对映射集合N⊂Ef×E0，表示为

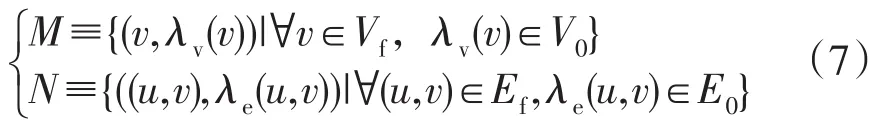
如果Gf与G0子图同构，那么可以推断Gf的任意子图也与G0子图同构。

定义集合M1为集合M中节点对的第1个节点的集合，定义集合M2为集合M中节点对的第2个节点的集合，即

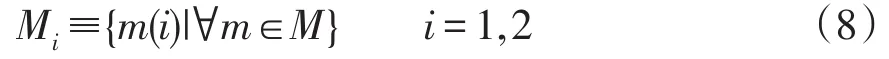
同理可以定义集合Ni为

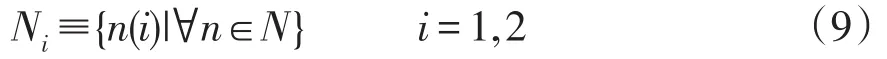
节点对映射集合M可以用大小为|Vf|×|V0|的0-1矩阵TM来表示，称为节点转移矩阵。TM的第i行j列元素mij=1表示Vf中的第i个节点与V0中的第j个节点构成一对节点对。

同样可以定义大小为|Ef|×|E0|的0-1矩阵TN来表示边对映射集合N，称为边转移矩阵。TN第i行j列元素nij=1表示Ef中的第i个节点与E0中的第j个节点构成一对边对。

同构子图定义：满足式（5）关系的映射λv、λe的节点与边的最小集合，形成的图，称为Gf在G0中的同构子图，记作，显然有

1.2 电力系统故障模型

电力系统故障可以抽象为简单无向图Gf上所发生的一系列动作，称Gf为故障网络。每类故障发展路径、故障动作时序都有所差异。定义网络模式函数α(Gf)、事件集合Kf以及事件模式函数β(Ef)分别刻画故障发展路径、故障过程中发生的事件的集合以及事件与边的映射关系。

1.2.1 网络模式

其中diag[]表示对角矩阵。

具有相同网络模式函数的两图一定是满足式（5）的同构子图，即

1.2.2 事件集合

定义事件集合Kf为故障发生过程中Ef上发生动作、位置与时间组合的集合，即

式中：ki为某条边上发生的事件；ai为故障发生的动作；li为ai发生点所在边的位置；ti为ai发生的时间。

例如ki=（单相断开，5%，1.05）表示1.05 s在某边5%的位置单相断开。

1.2.3 事件模式

定义事件模式函数β(Ef)≡[βij]|Ef|×|Kf|为大小|Ef|×|Kf|的0-1矩阵，表示集合Ef与故障Kf的映射，即

式中：Ef[i]为Ef的第i条边；Kf[j]为Kf的第j个事件。

例如，如果在β(Ef)的第i行中有βix=1，βiy=1，其余全为0，表示Ef中第i条边会发生Kf的第x个和第y个事件。

至此，完成了电力系统故障模型的数学描述，某一类型的电力系统故障的所有信息可以通过α(Gf)、Kf、β(Ef)三元素完整描述。

1.3 电力系统故障建模数学表达

电力系统构成的图记为G0=(V0,E0)，称为目标网络。故障网络Gf对应的网络模式矩阵为，事件集合Kf，对应的事件模式矩阵为β(Ef)。

2 基于子图同构的电力系统故障建模方法

2.1 故障建模算法推导

每个满足式（15）条件的节点转移矩阵TM就确定了1个Gf到G0的子图同构关系，定义矩阵P为

当式（15）等价于条件

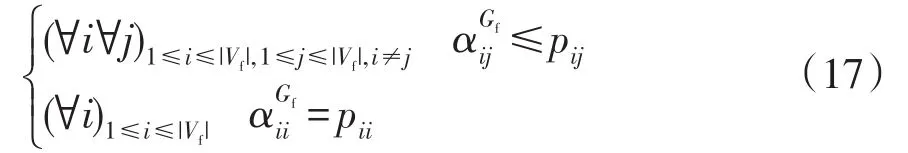
2.2 算法状态空间及约束

算法的最终目的遍历所有满足条件的矩阵TM。由于同构子图的任意子图都能在目标图中找到同构的关系。大部分高效的同构算法都选取深度优先的回溯算法[23]，并在分支过程中尽量剪枝，避免大规模的组合搜索，以提升算法效率。以下分别介绍算法的状态空间以及状态约束。

2.2.1 状态空间

定义si(i=0,1,…,|Vf|)为搜索状态，i为当前状态在搜索树中的深度。si表示已经在G0中为Gf中的前i个节点找到配对节点，也就是Gf中的前i个节点及其节点之间的边构成的图与G0子图同构。Gf中的前i个节点的集合定义为M1(si)，G0中对应匹配的i个节点的集合定义为M2(si)，状态si对应的节点转移矩阵TM(si)表示Gf中的前i个节点与G0所有节点的映射关系。

s0=∅，TM(s0)=1。当搜索深度i达到Gf节点数|Vf|时，就得到了1个候选矩阵TM；当搜索深度i未达到|Vf|时，选择Gf第i+1个节点u与G0尚未选择过的1个节点v，形成节点对(u,v)，构造下一个状态si+1。

2.2.2 状态约束

状态由si转化至si+1时，假设新加入的节点对为(u,v)，TM(si+1)相当于在TM(si)基础上增加一行单位向量εz，其中z是新加入的节点v在V0中的位置，即V0的第z个节点，即

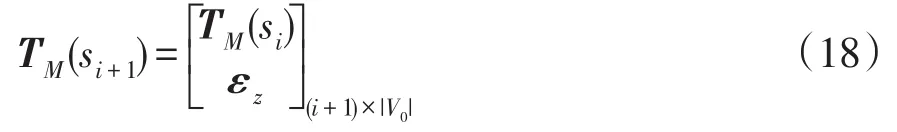
通过式（16）计算P(si+1)，判断P(si+1)是否满足式（17）条件。满足则称状态si+1是一致状态，继续搜索；否则称状态si+1是非一致状态，停止该分支上的搜索程序。式（17）的条件进一步推导得到Rule0、Rule1和Rule2三层约束如下。

Rule0：拓扑约束与节点类型约束。拓扑约束表示节点u在Gf中的度不能大于节点v在G0中的度，节点类型约束表示与节点u配对的节点v必须有相同的类型。此约束条件可以作为搜索状态si+1中节点v的搜索范围Ni+1，在程序初始化时进行计算为

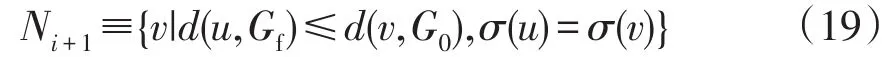
Rule1：待选节点不能与已选节点相同，即

Rule2：新加入的节点对(u,v)，对于新状态si+1则有

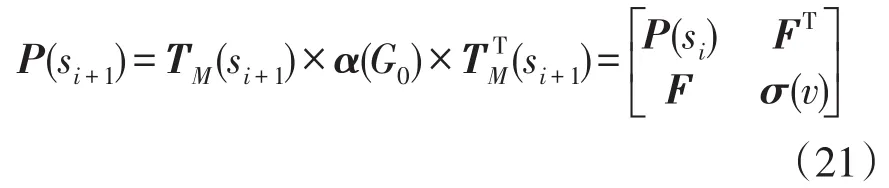
由于si是一致状态，即矩阵P(si)满足式（17）的约束，且由于式（19）节点v的搜索范围Ni+1的限制保证能够满足式式（17）中第2式的约束，因此状态si+1是否是一致状态，等价于矩阵F满足条件

除此之外，对于新加入的节点对(u,v)，v与V0中尚未选择的节点的关系应该能够包含u与Vf中尚未选择的节点的关系[23]。在故障建模中，假设图Gf的所有的节点类型为式（3）表示的q类节点，约束Rule3可以表示为

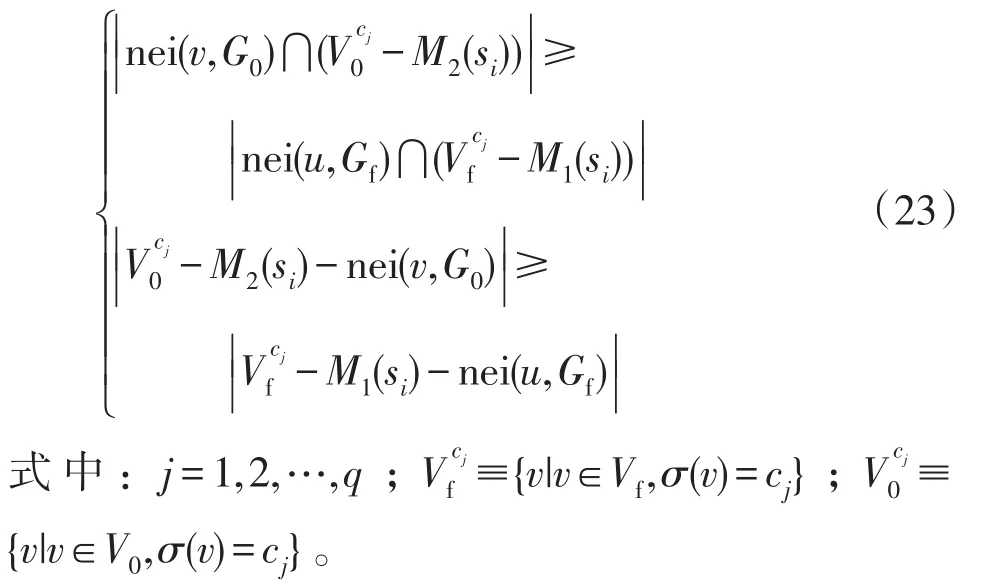
2.3 考虑电力系统网络特征的优化

为了模拟电力系统中发生的各类故障，不同的电力系统仿真软件的数据组织形式不同。例如在电力系统综合稳定程序（PSASP）中，为了模拟带高抗的线路，设计了高抗节点；为了模拟500 kV厂站3/2接线的配串信息，设计了分支节点。图1表示了1个包含3个变电站的局部电网中在PSASP中的可视化数据结构。甲变电站包含主节点“甲50”、分支节点“甲51”、“甲52”、“甲53”、“甲54”，同时还具有1个高抗节点“甲丙1”。数据结构包含实体边和虚拟边两种类型的边。该局部电网共有3条实体边：“甲丙1-丙 53”、“甲53-丙51”以及“甲 54-乙51”以及8条虚拟边，虚拟边仅表示站内母线分串等结构信息。

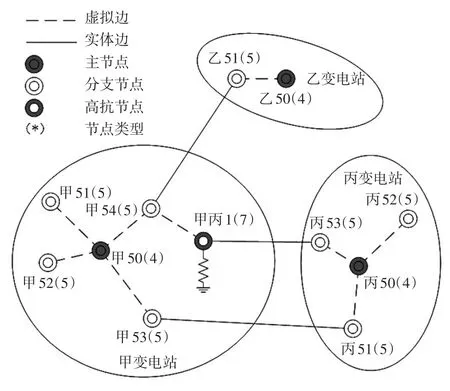
图1 典型PSASP仿真软件下的电网数据结构Fig.1 Typical data structure of power grid in simulation software PSASP

电力系统计算网络的特点是节点类型上来说，大多数为分支节点，少数为高抗节点、串补节点、串抗节点，主节点处于中间数量。图1中分支节点数量最多为8个，其次是主节点3个，最少的是高抗节点数量为1。

回溯算法的加速方式主要是剪枝操作。由于算法中需要逐个加入Gf中的节点，因此故障网络的搜索顺序十分关键。因此需要在算法中加入全网节点类型分布分析，优先在搜索树中选择类型数量分布较少的节点，能够有效减少每一级分支数量。

在确定Gf中的节点搜索顺序之后，还需要充分利用故障网络Gf已有信息，在搜索过程中尽早去掉非一致状态。在实际电力系统仿真实践中，基于调度命名的仿真数据节点名称本身就蕴含了部分网络拓扑信息。电力系统计算网络节点语意是通过对节点命名分析得到的特征文本，记作τ:V→H表示集合V中每个节点的特征文本hi∈H，即

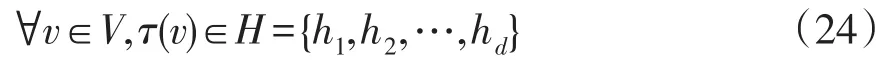
式中，d为节点特征文本的个数。

在状态si下，定义M1(si)中节点的语意集合H1(si)与M2(si)中节点的语意集合H2(si)分别为

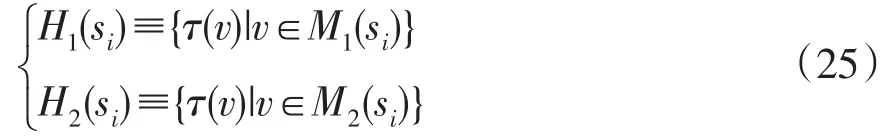
针对Gf搜索顺序第i+1级的节点u，需要寻找其语意父节点u＇，即

Rule4：一致状态si，加入的节点对(u,v)仍保持一致状态，节点v需要满足约束

在搜索同构子图过程中考虑节点语意意味着能够缩小选择的范围，极大提高搜索效率。式（26）语意分析过程能够在确定Gf节点顺序之后，搜索开始之前进行预处理。综上，基于子图同构的电力系统故障建模方法流程如图2所示。

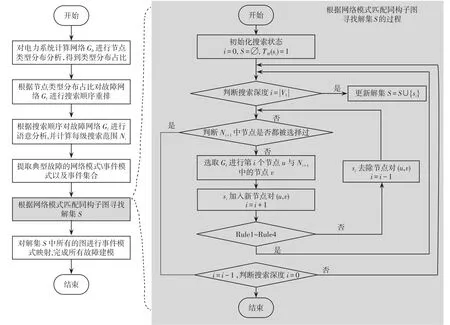
图2 基于子图同构的电力系统故障建模方法流程Fig.2 Flow chart of power system fault modeling method based on subgraph isomorphism

3 算例分析

3.1 局部电网算例

以图1所示的局部电网计算网络为例，发生在典型不带高抗线路“甲54-乙51”上的N-1故障，在建模中体现为1.0 s时“甲54-乙51”线路在2%处三相接地短路，“甲54-乙51”线路两侧断路器分别在1.09 s和1.1 s，跳开以隔离短路故障。在PSASP中不带高抗线路的两侧断路器位置一般设置在线路的1%、99%处。整个短路时序及位置如图3所示。整个N-1故障的物理过程以及建模体现形式如表1所示。此故障属于不带高抗的线路发生的N-1故障，应用本文算法挖掘该局部网络中所有与此类故障形式相似的故障。

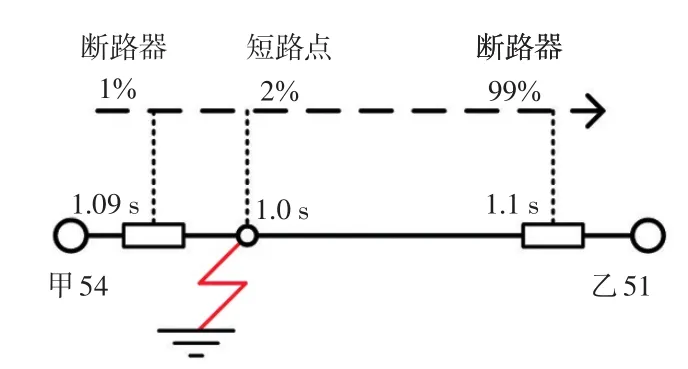
图3 不带高抗线路N-1故障在PSASP软件中的设置Fig.3 Configuration of typical N-1 contingency in software PSASP

局部电网G0的节点集合V0={甲50，甲51，甲52，甲53，甲54，甲丙1，乙50，乙51，丙50，丙51，丙52，丙53}，边集合E0={（甲50-甲51），（甲50-甲52），（甲 50-甲 53），（甲 50-甲 54），（甲 54-乙 51），（甲 54-甲丙1），（甲丙 1-丙 53），（甲 53-丙51），（乙50-乙 51），（丙 50-丙 51），（丙50-丙 52），（丙 50-丙53）}。

该故障形成的图Gf的节点集合Vf={甲54，乙51}，边集合Ef={（甲54-乙51）}。该故障的网络模式，事件集合以及事件模式如表1所示。

表1 不带高抗线路N-1故障的网络模式、事件集合和事件模式Tab.1 Network pattern,event set and event pattern under typical N-1 contingency

对于G0有

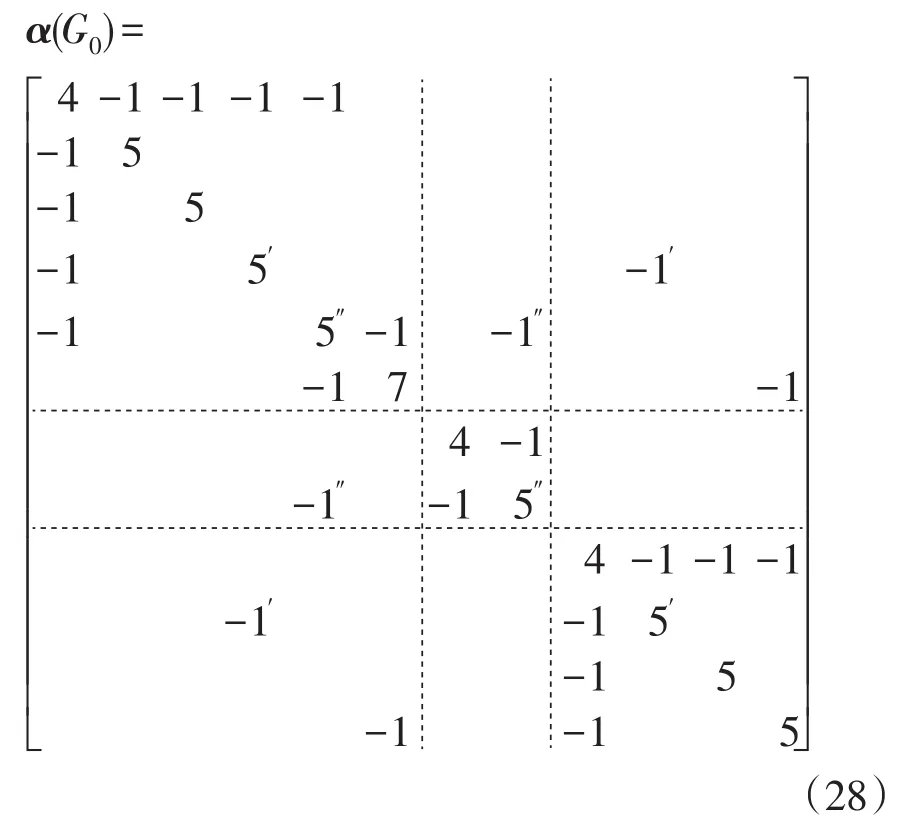
显然，式（28）中带单撇“＇”标记的4元素与带两撇“″”标记的4元素组成的2个2×2矩阵与表2中的α(Gf)均满足式（17）的条件，这2个满足条件的节点转移矩阵分别为

式（29）中2个节点转移矩阵代表了2个与Gf相同的结构即：（甲53、丙51）、（甲54、乙51）。再利用β(Ef)与Kf进行故障时序的分配可以得到该局部电网中2个与Gf同类故障，即线路“甲53-丙51”N-1故障与“甲54-乙51”N-1故障。

3.2 区域电网算例

选取国内某较大规模的500 kV区域电网在PSASP中对应的计算网络G0，该网络有703个计算节点，818条计算边。下文算法运行的硬件环境为CPU：Intel（R）Core（TM）i7-6700HQ，主频 2.60 GHz，内存8 GB。操作系统为Windows 10-20H2。

3.2.1 算法效率分析

1）目标网络G0节点顺序影响

为了研究目标网络G0节点顺序对算法的影响，本文通过100次随机生成目标网络节点顺序，记录了针对单侧带高抗线路N-2故障建模的算法耗时。仿真过程中每次运行时间如图4所示，单侧带高抗线路N-2故障建模平均耗时2.459 s。

图4 不同目标网络节点顺序下，单侧带高抗线路N-2故障建模时间Fig.4 Modeling time of N-2 contingency which occurs on lines with shunt reactor on single side with different target network node sequences

采用上述抽样方法，表2记录了不同类别故障建模平均用时。其中“中开关拒动故障”是指3/2接线中断路器在出线短路后拒动，进而引发后备保护动作，跳开同串边断路器以及同串出线末端断路器的连锁形式的故障；“双重中开关拒动故障”是指在“中开关拒动故障”的基础上，后备保护中同串出线末端断路器拒动而继续引发下一级后备保护动作的连锁故障。以上两种故障均是继电保护拒动而可能引发的连锁故障，是与运行方式无关且可以准确描述、建模的连锁故障。利用本文方法，以上2类故障建模仅需1.362 s、0.735 s。本文方法不仅能够快速建模N-1、N-2等传统故障，还能够适应连锁故障建模。

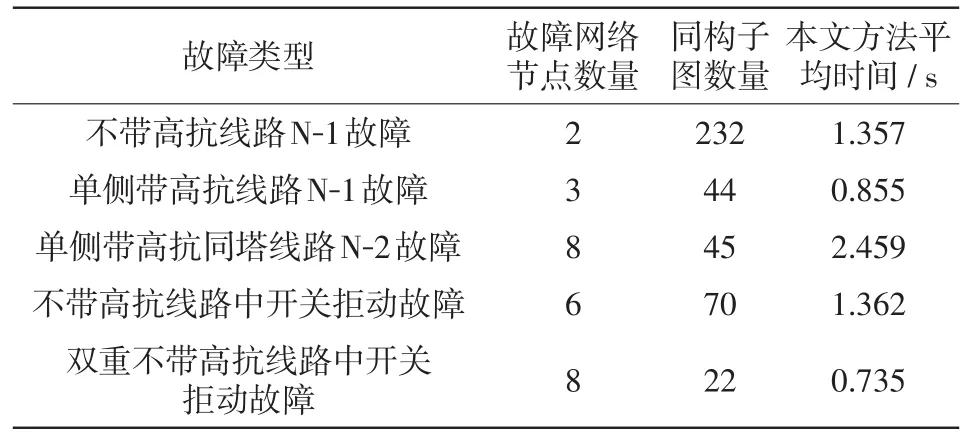
表2 不同类别故障建模本文方法平均用时Tab.2 Average time consumption by modeling different types of fault using the proposed method

2）故障网络Gf搜索顺序影响

G0节点的类型分布如图5所示。考虑电力系统网络特点，Gf节点搜索顺序按照类型分布概率由多到少和由少到多进行故障建模的算法耗时如表3所示。对于单一节点类型的故障网络，搜索顺序影响不大；对于多节点类型的故障网络（例如表3中单侧带高抗线路N-1故障、单侧带高抗线路同塔N-2故障），故障网络Gf搜索顺序十分关键，本文方法有良好的搜索效率。

图5 区域电网节点类型分布Fig.5 Node type distribution in regional power grid

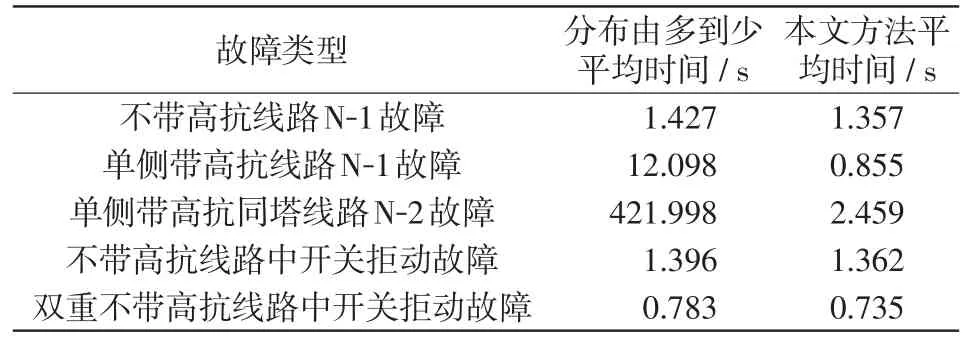
表3 故障网络搜索顺序对故障建模用时影响Tab.3 Impact on time consumption by fault modeling with different search sequences of fault network

3.2.2 不同建模方法对比

VF3方法[23]与本文方法故障建模的所需时间对比如表4所示。由于未考虑节点语意信息，在不带高抗线路N-1故障建模中，VF3算法平均用时低于本文提出方法，略有优势。但同样由于未考虑节点语意信息，随着故障复杂程度增加，对比本文方法，VF3算法效率下降，识别结果出现了不准确的情况。例如在单侧带高抗线路N-1故障识别的过程中，同一故障路径的正序、反序被重复识别了2遍；缺失对“同塔”语意的处理，导致单侧带高抗同塔线路N-2故障不仅重复识别，甚至识别出非同塔N-2故障。因此基于子图同构的电力系统故障建模方法中，考虑节点语意是必要的。

表4 VF3方法与本文方法故障建模所需时间及准确度对比Tab.4 Comparison of time consumption by fault modeling and accuracy between VF3 method and the proposed method

图计算方法[6]与本文方法故障建模的所需时间对比如表5所示。2种方法建模耗时均为秒级，而图计算方法总体速度甚至超过了本文算法。原因是图计算的方法根植于对电网计算数据的深入人工分析，针对特定故障的优化能够保证图计算方法较高的效率。但随之而来的缺点是适用性差，依赖所研究电网的数据组织形式，无法随时切换到其他地区或者其他仿真平台。

表5 图计算方法与本文方法故障建模所需时间对比Tab.5 Comparison of time consumption by fault modeling between graph calculation method and the proposed method

随着故障的复杂程度增加，有限人工经验总结的图计算的方法无法更加充分地利用节点语意等故障信息，多重循环下故障路径搜寻的效率将不断下降。例如在双重不带高抗线路中开关拒动故障建模中，图计算方法所需时间1.417 s大于本文方法平均用时0.735 s。本文方法在复杂故障建模中更具优势。

3.2.3 对电力系统结构、运行方式及仿真数据结构的适应性

通过应用本文方法对该区域电网历史数据（选取2019年）以及本年度检修方式数据以及本年度PSD-BPA（电力系统仿真软件，与PSASP仿真数据结构不同）数据进行不带高抗线路N-1故障建模，均得到该电力系统结构、运行方式以及软件数据结构下完整的故障集合，所用时间对比如表6所示。

表6 本文方法适应性验证Tab.6 Adaptability verification of the proposed method

对比可见，不同仿真软件下的数据结构不会影响最终故障集合里故障的数量。检修方式下，故障数量会降低；随着电网的发展，不同年度的故障数量会随设备的投产、退役有增有减，随着各区域电网特高压交流项目推进，现有常规电压等级网架结构优化分析以及调度运行将更加依赖快速、准确的故障建模方法。

本文提出的基于子图同构的电力系统故障建模方法效率能够满足大型区域电网在线安全分析校核的需要，同时也能够为电力系统离线仿真分析提供可靠支持。本方法优点是：不依赖所研究电网的数据组织形式，可以一次开发，随时部署到任意区域电网、任意仿真平台中使用；还能够适应复杂故障的全网建模。

4 结语

本文通过对电力系统故障模型进行了统一的数学表达，分析了故障建模的数学实质，结合电力系统网络节点类型分布与节点语意信息特点提出了基于子图同构的电力系统故障建模方法。区域电网算例结果表明本文提出的方法立足于图论基础理论，不依赖具体数据结构，能够实现电力系统仿真故障模型快速精准建模。本文方法具备推广到互联网、供气、供热、供水、交通等物理网络仿真故障建模的可能性，未来将在相关领域可以进一步提炼。