用瞬时值对称分量计算不对称短路电流直流分量衰减时间常数

曹 炜，李 芸，陈春阳

（1.上海电力大学电气工程学院，上海 200090；2.国网信阳供电公司，信阳 464000）

随着电力系统的发展，为降低损耗，各主要一次元件如发电机、变压器、输电线的电抗电阻比越来越大，导致系统短路电流中的直流分量衰减越来越慢[1]，而为限制短路电流使用的串联电抗和高阻抗变压器[2-3]更加剧了这个问题。对于短路电流直流分量衰减的计算，缺乏工程上简单实用的方法和工具，而对于不对称短路甚至缺乏计算直流分量衰减时间常数的理论。

要想计算不对称短路电流中的直流分量，目前只能用电磁暂态仿真软件，如EMTP进行三相全相电磁暂态建模与仿真，得到短路全电流，再从中分离出直流分量。由于EMTP建模和计算都非常复杂，将其用于大型网状网络计算，工作量非常大，一般仅在特殊情况下需做详细研究时使用，而不用于电网企业的日常例行计算[4]。

由于缺乏简便易行的计算方法，短路电流计算相关标准对直流分量计算的陈述都较简单，国家标准GB1984—2003对三相短路推荐固定经验时间常数（45 ms、62 ms、95 ms，体现在冲击系数中分别为1.80、1.85、1.90）来考虑直流分量的衰减[5]，同时推荐使用等效频率法计算和直流分量衰减相关的三相短路冲击系数。国际标准IEC60909-0[6]虽然提及了不对称短路，但只是建议不对称短路时使用三相短路时的冲击系数。由于冲击系数由直流分量衰减时间常数决定，该标准也隐含了不对称短路时直流分量衰减时间常数参照三相短路考虑。上述标准中推荐的数值能否反映系统的实际情况难以确定，同一地点三相对称短路与各类型不对称短路情况下直流分量衰减的时间常数是否相差不大也缺乏理论根据。因此无论在电气系统设计时进行电气设备（尤其是断路器）的选择和校验，还是在电力系统运行时进行断路器开断能力、关合能力的例行校核，都存在一定的盲目性[7-8]。

目前，我国经济比较发达的京津唐、长三角、珠三角地区和我国西北电源密集区域都出现了短路电流过大的情况，且有时发生概率更高的单相短路电流周期分量在数值上甚至超过三相短路电流周期分量，尽管经过各种限流措施，仍有相当一部分断路器运行在断流能力裕度很小的状况下[9-13]。工程实践中我国进行断路器断流能力例行校核时只考虑周期分量，并未计及直流分量对断路器开断能力的影响。但断路器需开断的电弧能量和短路全电流（包含周期分量和直流分量）相关[1，14]，即校核断流能力时需同时考察触头刚分时短路电流周期分量和直流分量。因此在断路器开断能力裕度较小时，需要更精确地估计断路器触头刚分开时的直流分量情况，而直流分量的衰减时间常数是影响短路电流中直流分量含量的重要因素。

本文基于120变换[15-19]的瞬时值对称分量，提出一种实用计算方法来计算不对称短路电流直流分量衰减时间常数。用EMTP仿真了不对称短路暂态过程，得到短路全电流，从中分离出衰减的直流分量[17]并计算出衰减时间常数，用于对比本文所提方法的短路电流直流分量衰减时间常数理论计算值，以校核本文方法的正确性和适用性。

1 120变换应用于不对称短路电流直流分量计算的原理

120变换是由abc坐标向120坐标的变换，它将a、b、c三相瞬时值变换到120坐标系中的1序量、2序量和0序量，是空间参照系的变换[20]，其变换矩阵与经典对称分量变换的变换矩阵完全一样，变换及反变换分别为

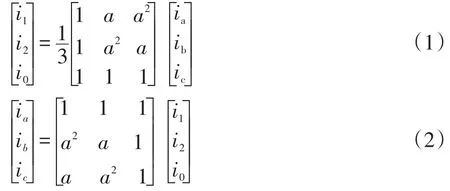
虽然两种变换方法变换矩阵相同，但120变换与经典对称分量变换存在本质区别。经典对称分量变换作用于相量，是时间变换，变换结果为abc三相中其中一相稳态或准稳态下正弦量相量表达的正、负、零序分相量；120变换类似于Park变换（变换矩阵与Park变换不同），作用于随时间变化的三相瞬时值。120变换将abc三相瞬时值看作abc坐标空间中一个综合矢量在abc坐标轴上的投影，该综合矢量在120坐标空间中1、2、0轴上的投影即1序量、2序量、0序量，即120变换是随时间变化的瞬时值在不同坐标系中的坐标变换[20]，可以用来分析任意暂态过程[16]。基于此，本文在分析不对称短路电流直流分量时不用经典对称分量法，而使用120变换，相应的序网络也不用经典对称分量法中对应相量时间变换的正、负、零序网，用对应瞬时值空间坐标变换的1、2、0序网代之，以免混淆。

上述2种变换应用于三相参数完全相同且存在互感的电力网络时，在变换后的坐标系中均可实现三序等值电路解耦：经典对称分量变换中表现为正、负、零序等值电路解耦，120变换中表现为1、2、0序等值电路解耦。当电力系统中包含同步机和异步机时，只要电机纵轴和横轴磁路参数完全相同，也同样可以实现1、2、0坐标的解耦。此时1、2、0等值电路分别类似经典对称分量法的正、负、零序等值电路，只是把正、负、零序等值电路中的jω算子用微分算子p代替[16]，且1序网络、2序网络中都有互为共轭的电源电势，其值由三相次暂态电势经变换而来，发电机电抗相应采用次暂态电抗，见图1。

图1 经典对称分量法与120变换的序网Fig.1 Sequence networks of classical symmetrical component and 120-transformation methods

目前，120变换在不平衡负荷校正[21]、功率因数校正[21]、有源滤波器设计[22]、逆变器暂态特性分析[23]、变压器方向保护[24]、矿井电网单相漏电的模型[25]、电压暂降检测[26]和谐波分析[27]中有一些应用研究，但这些研究针对的都是周期性变量，且多数文献主要针对工频量。此外，文献[28-29]对经典对称分量法进行了改进，尽管在标题中出现了“瞬时对称分量”，但实际上并非120变换意义上的瞬时值对称分量，因为改进方法变换的不是瞬时值而是相量，只是在计算相量时用到了变量瞬时值而已。

本文用120变换针对不对称短路全电流中的直流分量部分进行建模分析，推导直流分量衰减时间常数的计算公式。为此，当系统发生不对称短路时，搭建用于分析短路电流直流分量的1序、2序、0序等值电路，再根据不对称短路的边界条件构建出120复合序网分析短路电流中的直流分量。由于仅分析短路暂态过程中的直流分量，根据直流分量产生原理、电机定转子绕组各分量相互影响理论[30]和叠加原理，可得出分析短路电流直流分量的1序、2序等值电路中发电机电势均应为0。

对于同种不对称短路，边界条件无论是用相量表示还是用完整的瞬时值或者用作为瞬时值一部分的直流分量表示，其本质相同。以a相金属性接地短路为例，其原始边界条件为：故障端口的a相电压va为0，b相入地电流ib、c相入地电流ic为0，用故障端口的完整瞬时值表示为

只考虑va、ib、ic周期分量，并用相量表示为，边界条件为

a～、b～、c～的瞬时值表示为va～、ib～、ic～，则式（4）等价为

由于直流分量是短路后完整瞬时值与只考虑周期分量的瞬时值之差，所以式（3）与式（5）对应相减，即可得直流分量边界条件为

式中：va=为a相电压直流分量；ib=、ic=分别为b相、c相电流直流分量。

因为120变换与经典对称分量变换的变换矩阵完全相同，所以由式（6）推导出的1、2、0序网构成的120复合序网与由式（4）推导出的正、负、零序网构成的正负零复合序网相应序网的连接关系完全相同，其他类型不对称短路情况同样如此。

2 三种典型不对称短路下短路电流直流分量衰减时间常数的计算

为叙述方便，以下均假定a相为特殊相，并令特殊相直流分量的1序、2序分量分别为

式中：i1=、i2=分别为1序、2序直流分量，且互为共轭；ix=为实部，iy=为虚部，ix=、iy=均为实数。

将式（7）代入式（2）可得

式中：ia=、ib=、ic=分别为a相、b相、c相直流分量，均为实数；i0=为0序直流分量，i0=为实数。

2.1 单相接地

根据边界条件可推导出单相接地的120复合序网为1序网、2序网、0序网串联，，见图2。其中，i1=、i2=、i0=为直流分量的1序、2序、0序分量，且i1==i2==i0=，并均为实数。

由式（2）可知，短路点故障相的短路电流直流分量ia==i1=+i2=+i0==3i1=，所以故障相短路电流直流分量ia=及其1序、2序、0序分量都以图2中复合序网回路的时间常数衰减，表示为

图2 单相接地故障直流分量复合序网Fig.2 Interconnected sequence network for DC component under single-phase grounding fault

式中：L1Σ、L2Σ、L0Σ分别为1序网、2序网、0序网等值电感；R1Σ、R2Σ、R0Σ分别为1序网、2序网、0序网等值电阻。

2.2 两相短路

根据边界条件，两相短路的复合序网为1序网、2序网并联，也可以说1序网、2序网反向串联构成回路，见图3。其中i1==-i2==jiy=，均为纯虚数。代入式（9）、式（10）可得，即故障相电流正比于1序或2序电流。

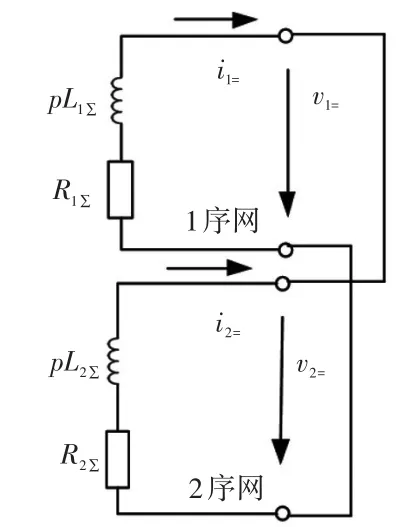
图3 两相短路故障直流分量复合序网Fig.3 Interconnected sequence network for DC component under two-phase short-circuit fault

所以，两相短路的故障相电流直流分量及其1序、2序分量都以图3中复合序网回路的时间常数衰减，表示为

2.3 两相短路接地

根据边界条件，两相短路接地的复合序网为1序网、2序网、0序网并联，见图4。

图4 两相短路接地故障直流分量复合序网Fig.4 Interconnected sequence network for DC component under two-phase short-circuit grounding fault

将b、c两相短路接地的边界条件ia==0代入式（8）可得

将式（13）代入式（7）可得

因此可根据图4推论如下。

（1）i0=流经的回路为0序网再串联1序、2序的并联网，以为时间常数衰减，则有

式中：Z1Σ、Z2Σ分别为1序网、2序网等值阻抗；ω为角频率（可选工频角频率或工频角频率的整数倍）。

（2）iy=流经的回路为1序网、2序网反向串联网，以为时间常数衰减，则有

而故障相的直流分量

为了便于用后续案例检验此推论的正确性，由式（17）、式（18）可进一步导出

所以，故障点的入地电流ib=+ic=将按照衰减，而故障点两故障相电流之差ib=-ic=将按照衰减。

3 各种不对称短路下直流分量衰减时间常数的实用公式

在用经典对称分量法时，图1（a）中的RiΣ、LiΣ用工频ωN下构成该序网的各元件阻抗R+jX等值变换求得。可以证明，当工频下各元件支路中的

对于隐极机Z1Σ=Z2Σ，由式（23）、式（25）、式（26）可知，两相短路时故障相短路电流直流分量衰减时间常数、两相接地短路时两故障相电流之差的直流分量衰减时间常数、三相短路时电流直流分量衰减时间常数均相等，即对隐极机而言，则有

需特别注意的是：如本文第1部分所述，在求R1Σ、X1Σ时，发电机支路的电抗需用对应的次暂态电抗而不是稳态电抗；如果经典对称分量法的各原始序网（即戴维南等值前）串联支路阻抗满足式（21），则式（22）～式（26）中所用序阻抗与经典对称分量法的序阻抗完全相同，且ω=ωN；当遇特殊情况（例如，将本方法应用于配电网络），如果经典对称分量法的各原始序网串联支路阻抗不满足式（21），则只需把经典对称分量法的各原始序网支路电抗ωNL替换为足够大倍数的工频电抗kωNL，使式（21）成立，再进行戴维南等值。即此时式（22）～式（26）中所用序阻抗与经典对称分量法的序阻抗不同，具体值由电抗增大后的戴维南等值决定，且式（22）～式（26）中ω=kωN。

4 算例分析

4.1 算例1

基于如图5所示的单机系统接线图，在EMTP软件上建立电磁暂态模型，元件主要参数如表1和表2所示。表1中的隐极机参数用于准确性检验仿真，凸极机1、凸极机2参数用于适应性检验仿真。表2中，RL(1)、RL(2)、RL(0)为输电线路正序、负序、零序电阻，XL(1)、XL(2)、XL(0)为输电线路正序、负序、零序电抗。

图5 单机系统接线图Fig.5 Wiring diagram of single-machine system

表1 旋转元件参数Tab.1 Parameters of rotating elements

表2 非旋转元件参数Tab.2 Parameters of non-rotating elements

设短路发生在输电线路中间位置，在不同线路长度下进行不对称故障仿真实验。再从仿真结果中分离出直流分量，并且拟合出其衰减时间常数[17]，作为式（22）～式（26）理论计算值的对比值，以检验本文方法的正确性和适应性。考虑到式（27）相等，故只需检验其中之一。

4.2 准确性检验

表3 单相接地故障直流分量衰减时间常数Tab.3 Attenuation time constant for DC component under single-phase grounding fault

表4 两相短路故障直流分量衰减时间常数Tab.4 Attenuation time constant for DC component under two-phase short-circuit fault

两相短路接地故障的直流分量衰减时间常数如表5所示。表5中，两相短路接地时入地电流直流分量ib=+ic=的衰减时间常数和故障相电流直流分量之差ib=-ic=的衰减时间常数的理论计算值分别与其相应EMTP仿真值TEmtp的最大相对差1和最大相对差2只有1.2%和0.2%，证明了式（24）、式（25）的正确性，即两相短路接地时总的入地电流直流分量ib=+ic=按衰减，故障相电流之差ib=-ic=以衰减。

表5 两相短路接地故障直流分量衰减时间常数Tab.5 Attenuation time constant for DC component under two-phase short-circuit grounding fault

除去作为反衬的表5中上述两列外，从表3～表5可知，仿真计算和理论计算的相对差都非常小，且有时表现为正，有时表现为负，这是因为EMTP直接仿真计算所得为短路全电流瞬时值波形，在用算法[17]将短路全电流中的直流分量与周期分量分离时会产生一定误差，由分离出来的直流分量拟合其衰减时间常数时又会产生一定误差。

由表3～表5还可知，单相短路故障相电流直流分量衰减时间常数、两相短路接地入地电流ib=+ic=的衰减时间常数与三相短路电流直流分量衰减时间常数（即各对应表中的或）差别较大，且线路长度越长差别越大：线路长度50 km时，表3、表5中对应的相对差分别为28.9%、54.54%。说明单相短路、两相短路接地的短路电流直流分量衰减时间常数如直接使用三相短路电流直流分量衰减时间常数会有较大误差。

三相短路故障直流分量衰减时间常数如表6所示。由表6知，当220 kV线路长度为10 km、50 km时，三相短路故障的EMTP仿真值TEmtp分别为147.5 ms、85.0 ms。该数据与文献[1]通过对数年前的上海输电网全网EMTP建模仿真得到的9处220 kV母线三相短路故障直流分量衰减时间常数（文献[1]中表1，具体数值在67.71～123.11 ms之间）大致吻合，而与传统的短路电流计算推荐采用的时间常数（45 ms、62 ms）相差极大。

表6 三相短路故障直流分量衰减时间常数Tab.6 Attenuation time constant for DC component under three-phase short-circuit fault

在传统的短路电流计算中当发电厂高压母线短路时，推荐的冲击系数为1.85，对应直流分量衰减时间常数62 ms；电厂升压变电站之外短路时推荐冲击系数为1.80，对应直流分量衰减时间常数45 ms。冲击系数是用来计算用于校核电气设备承受短路冲击电动力能力的冲击电流（发生在短路后10 ms左右）的，而传统短路电流计算中计算用于校核断路器开断能力的短路电流时，只考虑短路电流中的周期分量，不计直流分量。这种做法在触头刚分时故障电流直流分量含量为20%以下是符合国标[5]规定的。但问题是，即使假设直流分量衰减时间常数为推荐的45 ms，考虑短路较快切除的情况，设触头刚分时刻为短路后40 ms（根据数年前华东电网的统计，其超高压网中切除短路故障的时间在50 ms内的已达16%[32]），在最不利的情况下直流分量含量仍可高达41%；当直流分量衰减时间常数为80 ms时，40 ms触头刚分时直流分量含量更可能高达60%。所以，按照实际网络接线计算直流分量衰减有利于减少系统安全隐患。

考虑到本文方法计算直流分量的目的是为了选择和校核电气设备，例如，断路器的断流能力、关合能力等，而继电保护装置通常采用滤除直流分量的算法，所以本文论述的不对称短路直流分量时间常数的算法无论偏差如何对继电保护定值整定没有影响。

4.3 适应性检验

上述理论分析和仿真结果证明了由120变换法导出的式（22）～式（26）严格适用于隐极机，但电力系统中还可能会存在少量的凸极机（如水轮机），其中又以凸性较小的凸极机居多。单相接地故障、两相短路故障和两相短路接地故障的直流分量衰减时间常数分别如表7、表8和表9所示。由表7～表9可知，式（22）～式（26）应用于凸性较小的凸极机1所产生的相对差不大，在3%以下；应用于凸性较大的凸极机2所产生的相对差较大，但也未超过6%。

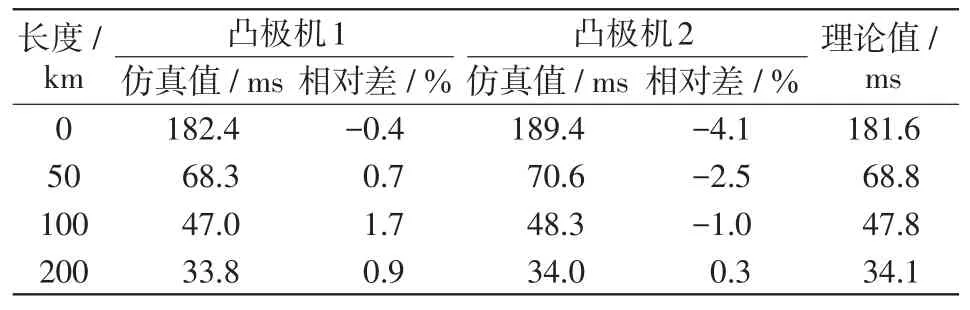
表7 单相接地故障直流分量衰减时间常数Tab.7 Attenuation time constant for DC component under single-phase grounding fault

表8 两相短路故障直流分量衰减时间常数Tab.8 Attenuation time constant for DC component under two-phase short-circuit fault

表9 两相短路接地故障直流分量衰减时间常数Tab.9 Attenuation time constant for DC component under two-phase short-circuit grounding fault

考虑到本文算例中仅有1台发电机，即整个系统100%由凸极机供电，尚且只有6%的相对误差；而实际系统中会有很多台发电机并列运行，凸极机2类型的发电机在整个系统所占比例极小，其提供的短路电流所占份额有限。鉴于此，如果以本文方法为基础，构建多机系统中短路电流直流分量的算法，可以预计由于凸极机原因带来的误差也不会大于6%。

表10为凸极发电机三相短路电流直流分量衰减时间常数，用式（26）计算所得与用EMTP仿真所得相差在3%左右，小于不对称故障下两者的差别（见表7～表9）。这是因为三相短路是对称故障，在理论上并不需要应用120对称分量法，即式（26）在凸极机下也是成立的，而式（22）～式（25）在凸极机下并不严格成立，所以需要这里的适应性检验仿真。

表10 三相短路故障直流分量衰减时间常数Tab.10 Attenuation time constant for DC component under three-phase short-circuit fault

4.4 算例2

以IEEE9三机九节点系统（其中1号机为凸极机）为例，设置变压器在高压侧接地，接线方式为D，yn11。在EMTP软件仿真其不对称故障过程，进而得到直流分量的时间常数[14]，作为本文方法的时间常数理论计算值的对比值。BusB单相短路、两相短路故障相的直流分量以及两相短路接地时入地电流直流分量的理论计算值和EMTP仿真值见表11。

表11 不同短路故障类型时间常数Tab.11 Time constants under different types of shortcircuit fault

由表11可知，典型不对称短路故障时本文方法求得的时间常数理论计算值与相应的EMTP仿真值相对差均在5%以内，再次说明了所提方法的正确性。

5 结论

（1）当发电机是隐极机，基于120变换推导出的式（22）～式（26）用来计算电力系统不对称短路故障中的直流分量衰减时间常数是正确的。

（2）当发电机是凸极机，本文方法仍适用，误差在工程计算可以接受的范围内。

（3）理论分析和仿真计算均表明两相短路故障相电流直流分量衰减时间常数与三相短路故障相电流直流分量衰减时间常数相同（隐极机时）或接近（凸极机时），其他类型的不对称短路故障相电流直流分量衰减时间常数与三相短路电流直流分量衰减时间常数相差较大，且在网络中线路越长，其相差越大。IEC60909-0标准[6]中推荐的各种不对称短路时仍用三相短路时的冲击系数的做法值得商榷。