融合时间序列趋势的Dual-ESN机组负荷预测模型
2023-02-13樊建升吴海滨刘泽军
樊建升,吴海滨,刘泽军
(1.山西焦煤能源集团股份有限公司,太原 030006;2.山西大学资源与环境工程研究所,太原 030006;3.古交西山发电有限公司,太原 030020)
现阶段,我国形成了以火电机组供电为主,新能源发电为辅的多元化新型能源结构[1]。受新能源装机容量的持续增加和用电负荷的间断性影响,电网发供电实时平衡主要依靠燃煤电厂进行调节,燃煤机组的负荷变化区间进一步增大,变化速率要求不断提高。为保证机组运行的安全性和经济性,需要探索机组负荷和多变量之间的演化关系,建立实时精确的机组负荷预测模型[2],以供工作人员参考负荷变化并及时调参。经典预测方法如指数平滑、回归分析和时间序列等,通常要求负荷数据具有良好的规律性,得到的预测模型简单[3],无法适应现阶段机组负荷数据复杂多元、预测模型精度要求高的需求。
基于大量历史数据,智能化方法越来越多地被应用在机组负荷预测的研究中。神经网络建模作为一种数据驱动的自适应方法,成为了主流的建模工具。前馈神经网络BP(back propagation neural network)、循环神经网络RNN(recurrent neural network)等已被广泛应用于机组负荷预测建模研究中[3-7]。然而,静态BP无法利用时间序列信息的问题,造成了结构性缺陷。RNN框架具有局部或者全局反馈连接,能够以“时间”先后次序处理工业数据,从而拥有更优越的动力学特性。但传统RNN迭代学习中存在梯度下降和消失的缺陷[8]。ESN摒弃了RNN中迭代学习的网络模型,只通过输出权值以类似回归方法求解,避免了上述缺陷。ESN应用于多种负荷预测,提高了预测精度[9-10]。
在真实工厂环境中,工程人员为了准确预估负荷的变化,通常更为关注相关变量和负荷本身的演化曲线,而不是单一数值。此行为的本质是,利用趋势和数值信息的互补依赖关系进行工况推论,来挖掘过程知识的潜在价值。在工业过程运行数据中,关键过程变量的趋势描述了数值随时间增长、变化的关系,体现了运行状况的变化趋向和速度,因此,数值信息和趋势信息对于预估过程运行状态都具有重要作用。综上,已存在的网络模型都是单一利用原始数据进行负荷预测,无法感知深层次的过程动态知识,从而影响整体框架的预测性能。
鉴于此,本文提出一种融合时间序列趋势的Dual-ESN机组负荷预测模型。该框架首先引入最小二乘法对有关的多元历史数据进行局部的线性段拟合,按照单位时间跨度划分为相应的斜率趋势序列。其次,原有的数值和趋势序列并行送入两个储备池结构中,形成高维空间向量。进一步,所有的高维向量融合进入伪逆解的回归层实现联合预测。此模型致力于捕获原有数值和潜在趋势之间的交互依赖关系,以融合学习的模式实现机组负荷的高精度预测。最后,基于山西某工厂660 MW机组正常运行工况下的数据集进行方法验证。结果表明,Dual-ESN所提出的框架存在更广阔的感知范围,可以适应复杂系统相对的动态变化,具有卓越的预测性能。
1 回声状态网络和多元时间序列
1.1 经典网络框架
相较于传统的RNN结构,ESN不同之处在于利用了稀疏连接的储备池结构代替传统的隐含层,其内部复杂的状态空间是对非线性时间序列潜在特性的表征。图1展示了ESN的连接结构,固有连接采用实线箭头描述,虚线箭头表示可以选择有或者无,整体工作流程解析如下。
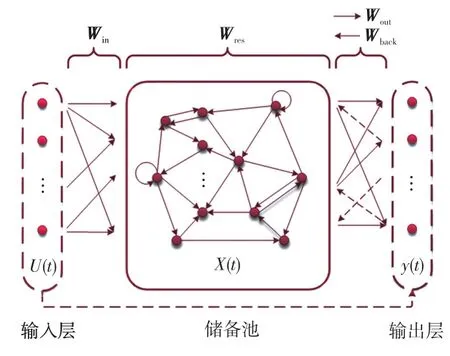
图1 ESN结构Fig.1 Structure of ESN
首先,设定左边输入层、中间储备池和右边输出层分别存在M、N、L个神经元模型。在t时刻,网络对应输入为U(t),储备池对应输入为X(t),输出为y(t)。
其次,初始化所有网络权值矩阵。其中Win∈ℝN×M为输入层与隐含层的连接权值向量;Wres∈ℝN×N为储备池状态更新的自连接权值向量;Wout∈ℝL×(N+M)为储备池与输出层的连接权值向量,此外内部还可能存在输出层对储备池的影响权值向量Wback∈ℝN×L。
随着序列数据的时间推进,储备池状态更新为
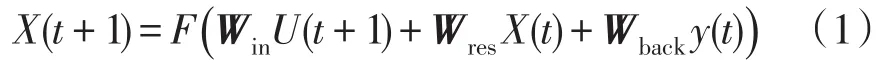
其中,Win和Wback通过多次随机计算得出,并在整个工作过程中保持不变。储备池中神经元的激活函数F(·)一般使用tanh或sigmoid进行嵌入。而在输出层的活性函数Fout可以是线性函数或者其他,最终可得ESN的输出状态方程为
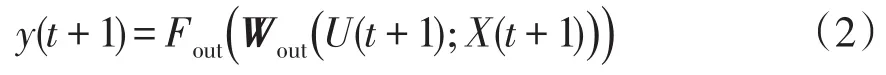
ESN可以被视为将数据于低维向高维进行空间映射,而后进行特征交互推演,在利用Wout得到预测输出。依赖类线性回归问题的解决思路,将输出与目标值的差距最小化可以计算得出Wout矩阵。此外谱半径SR归为(0,1)是回声状态网络稳定运行的必要条件,其目的是保正储备池架构的具体完备的回声特性,对应了连接权矩阵Wres最大特征值的绝对值。
由于ESN训练过程相对简洁,相关随机权值基于任务数据环境的改变而随之变化,最优的超参数需要多次经验测试才可确认。重要超参数包括谱半径、储备池中神经元个数、岭回归系数等[11]。由于回声状态网络特有的稀疏特性,其网络规模要比一般的网络大很多,储备池中其连接作用的神经元个数表征了整体网络的计算复杂程度。此外,工业时间序列的潜在特征变化可以用输出层权值的变化描述,也被视为短期记忆能力,越小则适用于相对稳定的工业数据环境,反之则可用于频繁变化的系统模型。
1.2 多元时间序列
过程运行数据主要以离散数值的形式被保存,这种数据本身只揭示了浅层且抽象的信息,例如,负荷450 MW,数值本身缺乏一定的实际意义。而时间序列的局部趋势涵盖了过程数据的动态信息,可以被视为数值变化的空间行为状态,即时间序列的向上或向下模式,如图2所示,其常见表征方式是斜率和持续时间[12]。但是实际生产运行中产生的大多是非线性动态的序列数据,无法利用斜率进行准确拟合。基于此,引入了最小二乘法[13],以直代曲的微积分思想实现趋势提取。
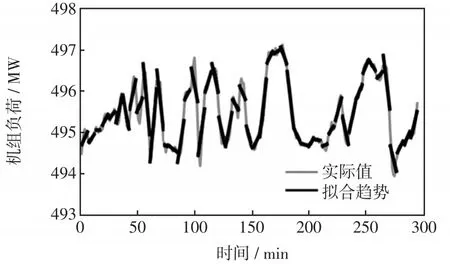
图2 机组负荷趋势序列辨识Fig.2 Unit load trend sequence identification
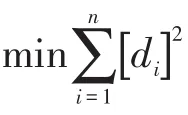
在上述理论的支持下,可以获得多元时间序列的局部趋势,在图2中,展示了真实负荷数据点上的线性端拟合结果,可以清晰地看到变量指标整体的演化走向。此趋势模式也必然影响了未来的变化程度。由此,多元趋势序列可以表征为一个二元信息组〈duration,slope〉。
2 融合时间序列趋势的dual-ESN机组负荷预测模型
受到工程师观测演化曲线推论未知工况的启发,斜率趋势和原有的数值被并行输入Dual-ESN框架以实现融合学习。此操作模式最大化地利用了相关联多元时间序列的过程动态信息,以提升机组负荷预测模型的性能。图3展示了Dual-ESN预测模型样例,其采用了典型的3层结构,即输入层、隐含层和输出层。首先,对工作原理进行阐述。拟定当前处于t时刻,网络的输入信号可以表示为
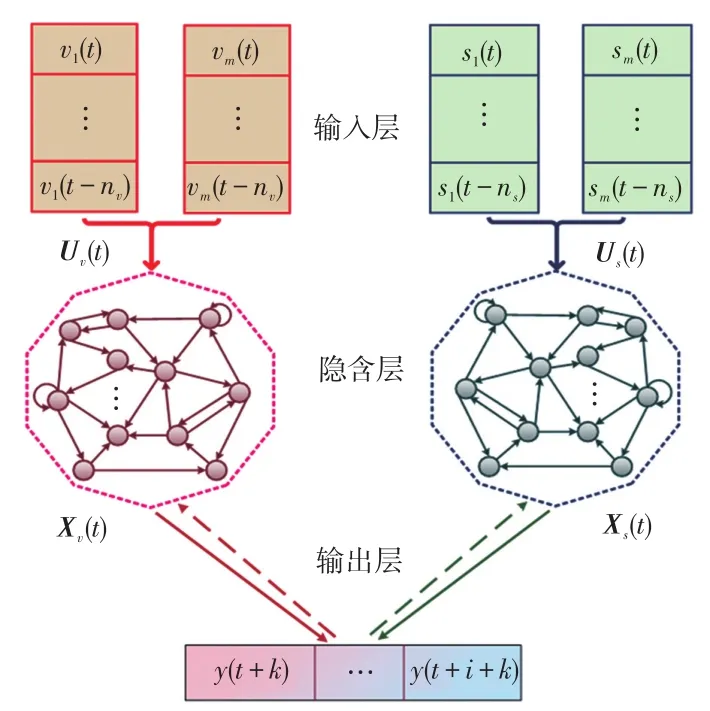
图3 Dual-ESN预测模型Fig.3 Dual-ESN prediction model
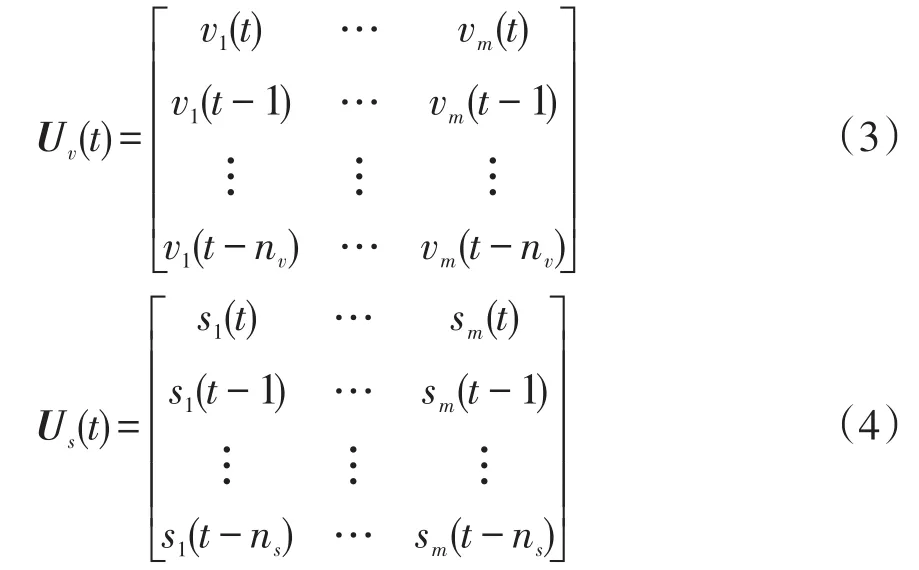
式中:vm(t)和sm(t)分别为t时刻的具体数值和趋势信息;m为输入的多元变量维度;Uv(t)和Us(t)分别为时间跨度内对应的输入向量;nv和ns为两者嵌入的时间跨度。由于在提取局部信息的斜率趋势时,已经进行了时间跨度融合。故在相同的计算复杂度底层结构中,nv>ns代表的感知视野。
相应地,储备池的状态向量X(t)描述为
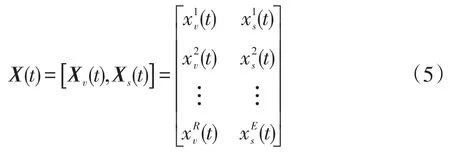
式中:Xv(t)和Xs(t)分别为数值和趋势信息对应储备池的状态向量;R和E分别为2个储备池中的神经元数量。以预测步长为k步的任务为例,模型的输出可以表示为
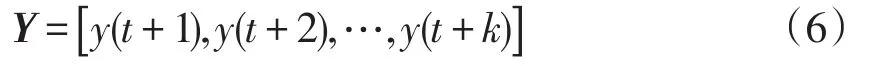
在上述设定下,储备池状态在t+1时刻的更新过程为
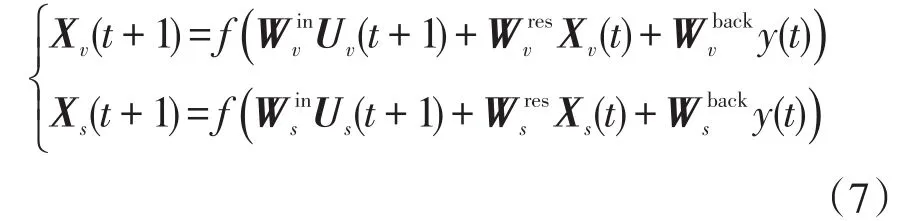
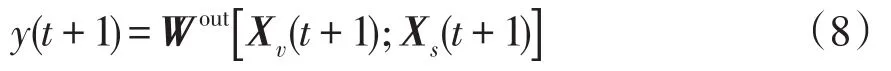
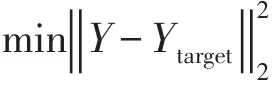
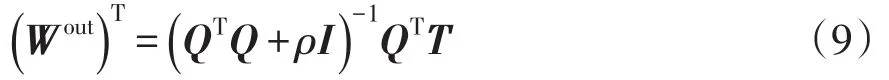
式中:I为单位矩阵;ρ为正则项系数;Q和T分别为在训练样本下的储备池状态矩阵和目标教师信号。此外,Dual-ESN不需要迭代训练,学习过程简单易行,从而不会面临梯度消失和爆炸的问题,而且时间消耗远小于经典的RNN框架,保持了负荷时序预测需求的实时性。
总结上述工作原理,得到本文提出的机组负荷预测方法流程,如图4所示。
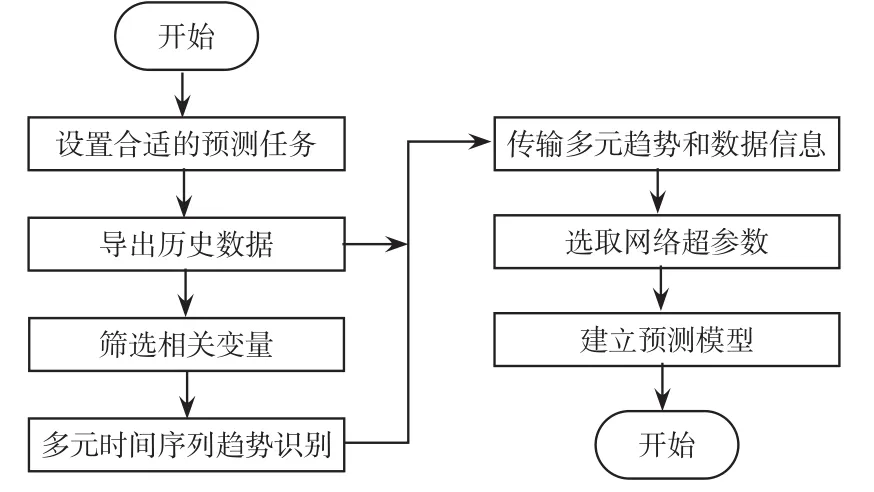
图4 流程图Fig.4 Flow chart
主要包含以下步骤:
步骤1从DCS或者霍尼韦尔的PHD数据库导出和机组负荷有关的多元历史数据,利用灰关联算法[14-15]和机组负荷动态过程知识进行多元变量的筛选,以排除相对的无关变量,从而提高工作效率。所使用灰关联算法其核心理论为根据曲线间相似程度来判断变量间的关联程度,因此广泛用于非线性系统的变量相关性分析。
步骤2对筛选后的数据进行预处理和归一化操作,完成数据准备,有

步骤3基于最小二乘法对预备的多元时间序列进行局部趋势识别,凭借设定的时间跨度获得工业过程变化的趋势序列。
步骤4根据实际的工程预测任务,选择契合的网络超参数,建立相适应的Dual-ESN模型。
步骤5并行输入趋势和数值序列,拟合预测目标完成模型训练。
步骤6对完备的Dual-ESN框架用于在线的时间序列预测,将预测输出反归一化可得出真实的工业数据。
3 实例研究
以太原某火电厂的5#660 MW超超临界机组[15]为研究对象,进行机组负荷预测。该厂采用了超超临界、三缸四排汽、一次中间再热、单轴、直接空冷凝汽式汽轮机。其回热系统包含1台除氧器、4台低压加热器和3台高压加热器。其运行过程如下:首先,通过锅炉给水、煤和风,燃烧后产生蒸汽;然后,将蒸汽送往汽轮机,在汽轮机中调节阀门开关度,带动发电机运转,获得所需的发电量,即机组负荷。图5所示为机组负荷的主要过程变量工艺。本文中选用的主要过程变量见表1。
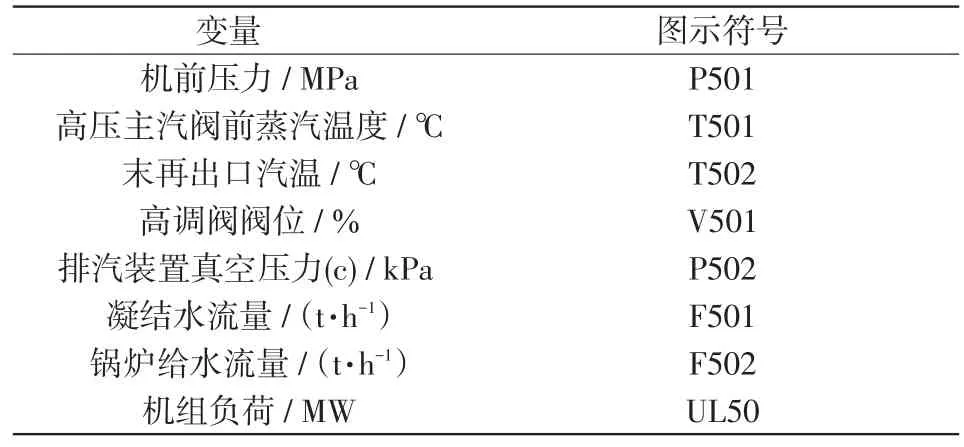
表1 机组负荷的主要过程变量Tab.1 Main process variables of unit load
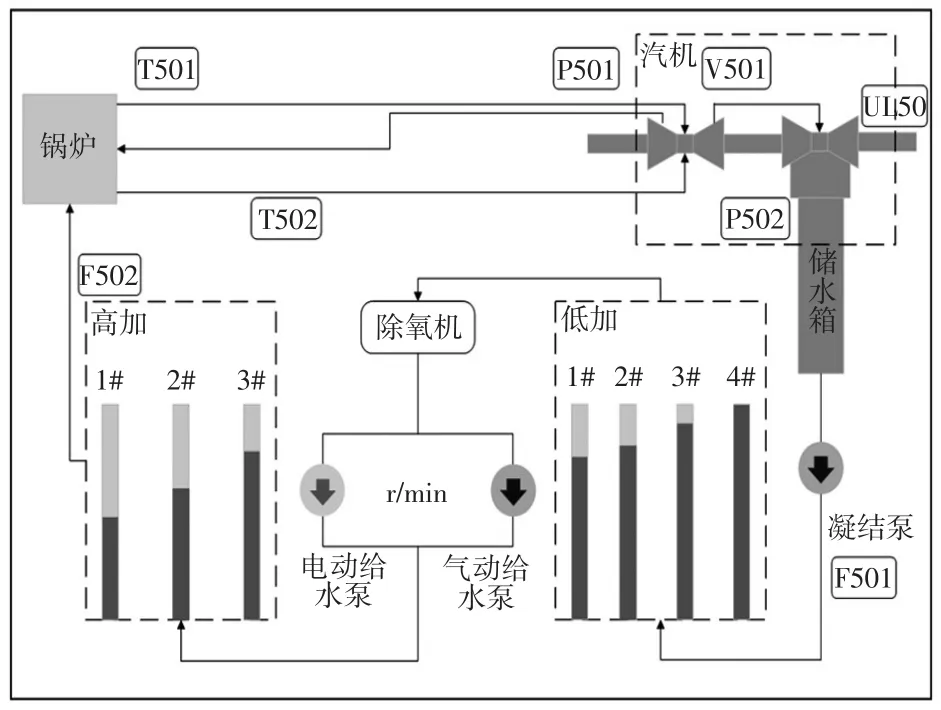
图5 机组负荷主要过程变量工艺Fig.5 Process of main process variables of unit load
选择该电厂5#机组在2021年冬季无检修、无故障停运的负荷数据,从历史数据库中导出相应多元时间序列,按照每分钟为采样节点收集10 000组样本作为实验数据,并按照6∶2∶2分为训练集、验证集和测试集。在此工业背景下,将ESN、Multilayer Perceptron(MLP)、Dual-MLP和所提出Dual-ESN完成对比实验,以验证模型有效性。
3.1 实验环境和评价指标设置
实验是在一台配备英特尔i7-7700中央处理器(3.50 GHz)和8.0 GB内存的个人电脑上进行的。Dual-ESN和其他神经网络算法都是基于Python 3.6.4和Keras环境下所搭建的。
通过2个常用于评估时序预测的指标,即均方根误差RMSE(root mean square error)和平均绝对误差MAE(mean absolute error),对机组负荷预测模型进行分析。两误差表示为
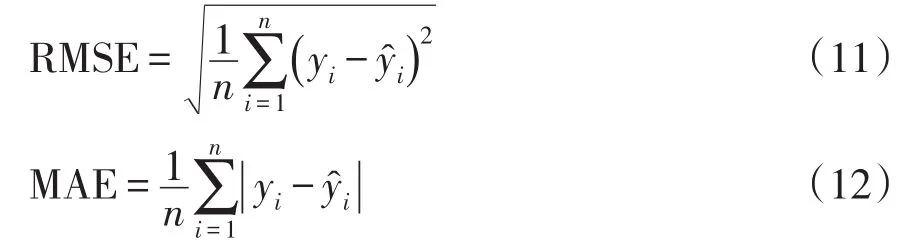
式中:yi为机组负荷实际输出值;为模型预测值;n为数据个数。在输入数据相同的情况下,对每个模型进行20次测试,取其平均值作为最终的预测误差。
3.2 时间序列趋势提取
首先依据灰关联算法得到所涉及变量的关联影响程度,相应的关联度热力分析如图6所示。
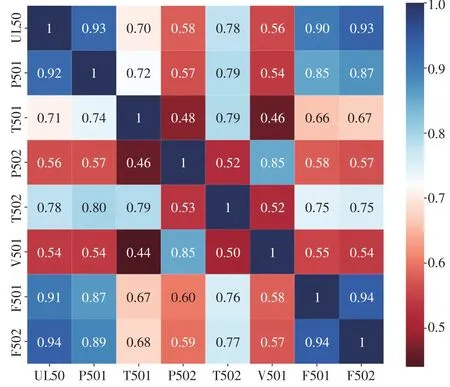
图6 主要过程变量之间的灰色关联分析Fig.6 Grey correlation analysis between main process variables
从中可以清晰地看出,机组负荷(UL50)分别与机前压力(P501)、凝结水流量(F501)、锅炉给水流量(F502)产生的灰关联度都在0.9以上,交互关系更为紧密。选择上述3个变量与机组负荷本身的历史数据作为神经网络模型的输入,执行符合实际需求的机组负荷短期预测。进一步,引入最小二乘算法对4个输入变量的历史时间序列进行趋势提取,结果如图7所示。
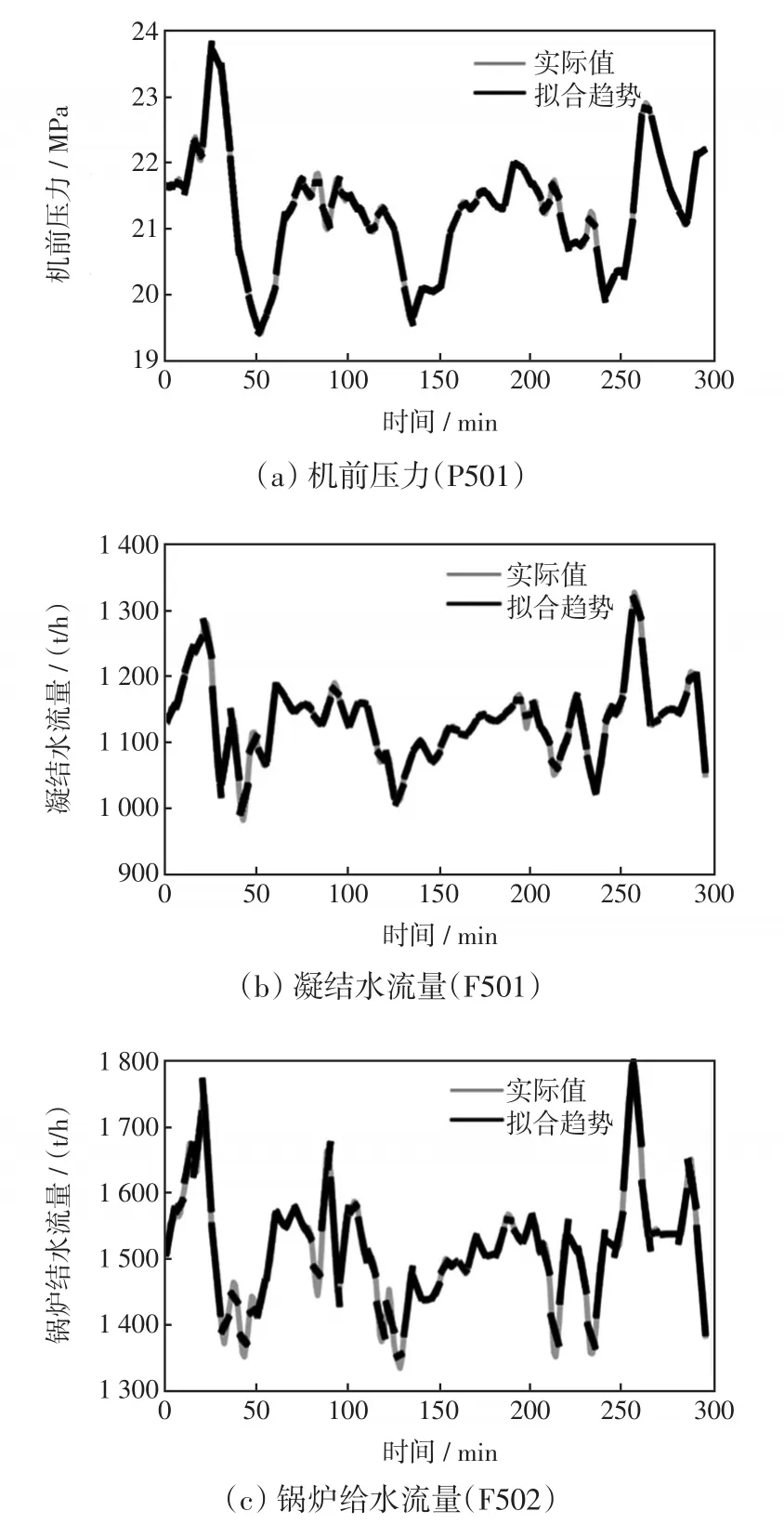
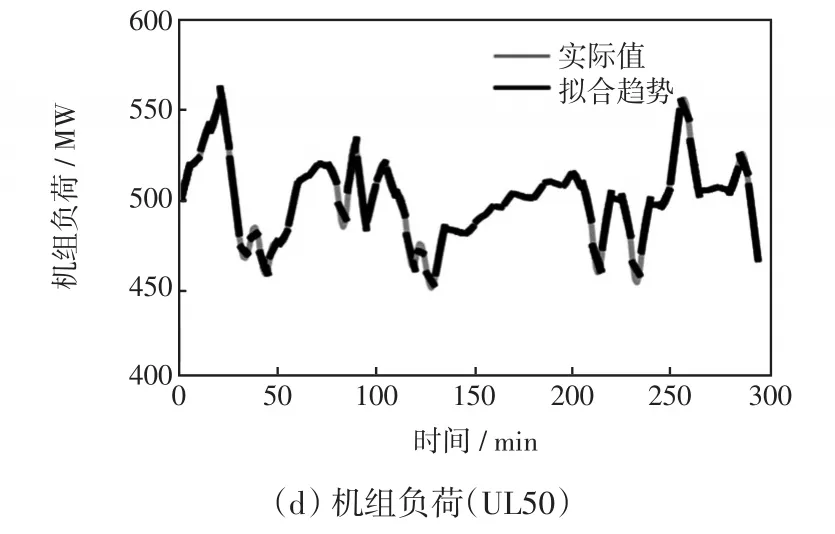
图7 过程变量的趋势序列辨识Fig.7 Trend sequence identification of process variables
设定固定的时间跨度,可以得到关于斜率的时间序列,可以从图7中的趋势走向推断下一时刻的工况状态,为精确地负荷预测提供了过程信息支持。此外,每一个线性段的趋势可以视作更多采样时间点的共生的潜在特征,如果在底层框架输入于预测模型,可以在不增加计算负担的情况下,提升Dual-ESN对于数据知识获取的感知范围。
3.3 实验对比
凭借Dual-ESN在训练集和验证集的表现,根据经验试错法选择网络的超参数,其中2个储备池规模都设置为300,权值矩阵Win在(-0.5,0.5)上随机分布采样,Wres的谱半径设为0.86。
选取机组不同运行时间内的机组负荷数据,以30个采样点为一组测试集,对比ESN和Dual-ESN在机组负荷测试集上的预测分布和残差估计。图8和图9分别展示了不同运行时间内的负荷预测分布和残差结果。从中可以明显地看出,Dual-ESN在多个时间阶段中都具有优越性。为了全面地分析趋势嵌入对预测性能的提升,额外补充了MLP和Dual-MLP的对比实验。其中,Dual-MLP为2个并行的前馈网络模型,同Dual-ESN类似,分别嵌入趋势和数值信息于终端进行特征融合。
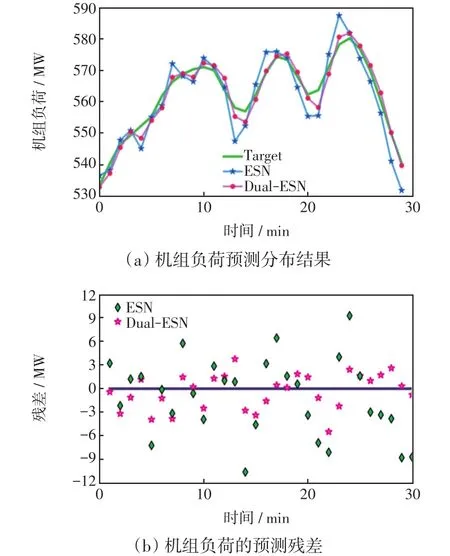
图8 ESN和Dual-ESN对于机组负荷的预测结果Fig.8 Prediction results of unit load by ESN and Dual-ESN
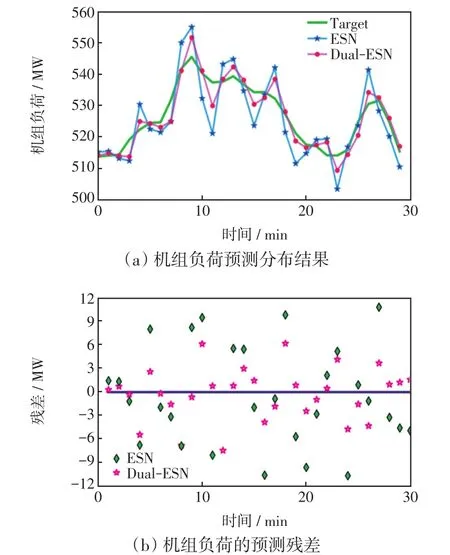
图9 ESN和Dual-ESN对于机组负荷的预测残差Fig.9 ESN and Dual-ESN prediction residuals for unit load
表2给出了所有模型的RMSE和MAE指标情况和训练时间。MLP利用了迭代学习的BP算法,但其静态的结构使得计算花销很低,和非迭代学习的ESN模型差距较小,相应的训练时间为30.6 s和21.2 s。根据RMSE指标分析,由于MLP无法利用时间序列“顺序”的重要信息,因此和ESN模型有的性能较大差距,结果分别为12.483 MW和7.832 MW,这对于工业的实际判断性操作参考的影响是非常巨大的。此外,值得注意的是,趋势信息的并行输入对于MLP网络同样有性能提升,在表2中,传统ESN的相应误差指标为7.832 MW和6.571 MW,相较于Dual-MLP的误差9.584 MW和7.562 MW,展现了一定的优势。在一定程度上可以说明,所提出的理论在不断更新的深度学习模型中具备推广意义,但是要注意各自模型的缺陷,以免限制了底层数据质量的利用。Dual-ESN模型相应的误差为5.957 MW和4.624 MW,具有全面的性能优势。在另一方面,Dual-ESN的相对的训练时间只有27.8 s,相对于Dual-MLP的44.5 s有明显的区分,这一差距在多层网络中还会加深。因此,在Dual-ESN预测模型对复杂工业特征保持较高的学习速率同时,实现了机组负荷的精确预测。
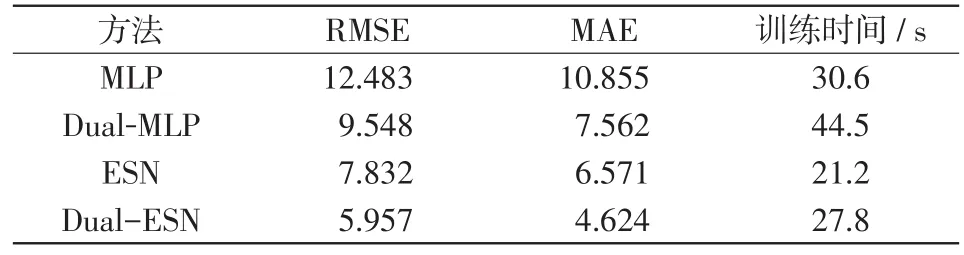
表2 不同模型对于机组负荷的预测精度Tab.2 Prediction accuracy of different models for unit load
4 结语
本文提出了一种融合时间序列趋势的Dual-ESN机组负荷预测模型。通过太原某工厂实例数据证明了所提出的模型具有如下优势:
(1)引入了最小二乘法对于影响机组负荷的多元时间序列进行趋势识别,充分提取了相关因素的潜在特征,获得了相应的过程趋势信息;
(2)通过嵌入多元趋势和原有数值信息,建立了完备的Dual-ESN模型,利用了预测目标对于当前趋势的依赖关系,实现了更高质量的特征传递;
(3)与传统的ESN、MLP以及拟定的Dual-MLP机组负荷预测模型相比,本文所提方法进行了趋势信息填充,能提供更长(宽)的历史数据信息,因而可以感知更宽广的历史视野,预测性能更为卓越。
