车用爪极发电机新型三维分段等效磁路法研究

杨宇哲，赵 博，孙金涛，张宗京，杨 鹏

(1.山东理工大学 电气与电子工程学院，山东 淄博 255000；2.山东山博电机集团有限公司，山东 淄博 255200)

1 引言

电励磁爪极发电机可靠性好，机械强度较高，对于工作环境要求不严格，被广泛应用于装甲车辆，坦克战车上。同时，因为其特殊的三维结构，也导致了该电机磁路长，漏磁系数高，以及多漏磁路径等缺点，降低了电机在使用过程中的效率，导致该电机的发电容量下降，致使装甲车辆中用电器的总功率容量提升困难。因此对爪极电机进行精确的解析计算，对研究和优化爪极电机的性能十分重要[1]。目前，针对爪极电机的特殊三维结构，国内外一般采用三维有限元法来进行精确计算，但因三维有限元法由于计算量大，计算时间较长，受到网格划分因素的影响，对于后期电机优化所要求的不同结构参数的电机计算以及分析造成困难。因此，运用解析法对电机进行解析计算有重要意义。

为建立较为精确的解析模型，文献[2]中以外永磁转子式爪极电机为例，建立了二维等效磁路，但该磁路模型没有充分考虑爪极电机主磁通的轴向分量，且对于爪极电机的漏磁考虑不够充分。文献[3-5]中都采用三维等效磁网络法对爪极电机进行解析计算，但三维磁网络法构建磁网络较为复杂，且计算结构受磁网络剖分单元影响较大，容易产生计算误差。文献[6]中利用麦克斯韦张量法建立了电磁力的解析模型，通过解析公式的方式对电机的气隙磁场以及径向电磁力进行计算。虽然对电机的三维结构特点考虑较为充分，但是没有考虑电机轴向磁通分量的影响。

对于爪极电机的解析计算，目前常用的方法有2种，分别是二维磁路模型解析计算和三维等效磁路法。二维磁路模型中对于漏磁以及多方向磁通的考虑不够充分，三维等效磁网络法构建磁网络时较为复杂，且对于磁网络的网格抛分要求较高。本文中依据现存的2种方法，综合2种方法的优点，基于原有二维磁路模型，本文中提出了电励磁爪极发电机的新型三维分段磁路解析模型，在充分考虑其不规则爪极形状的同时，考虑了多条漏磁支路的影响，推导出了各磁阻的解析计算公式，建立了电励磁爪极发电机的新型三维分段磁路模型。之后，通过三维有限元法验证了该种方法的准确性，为该种电机的后续优化工作提供了一种快速准确的计算方法。

2 爪极发电机的主磁路

电励磁爪极发电机励磁来源是固定在支架上的励磁绕组，在电机空载时，爪极电机的磁通主要分为两部分：主磁通与漏磁通，主磁通为穿过电枢线圈成为感应电势的磁通，漏磁通为未穿过电枢线圈的磁通。由于该电机特殊的三维结构，使得其主磁路与其他电机有本质区别，由励磁线圈通电后产生的轴向磁通，经过爪极结构后磁通改变方向，转化为径向磁通。爪极电机的主磁路如图1所示。由励磁绕组产生的轴向磁通，经过前爪极结构之后，转化为的径向磁通，通过主气隙进入电枢绕组，之后经过气隙通过后爪极形成闭合磁回路。在负载状态下，定子三相绕组中电流产生旋转磁动势，所以，该电机的气隙磁场是由励磁绕组与定子绕组中的电流共同作用产生。

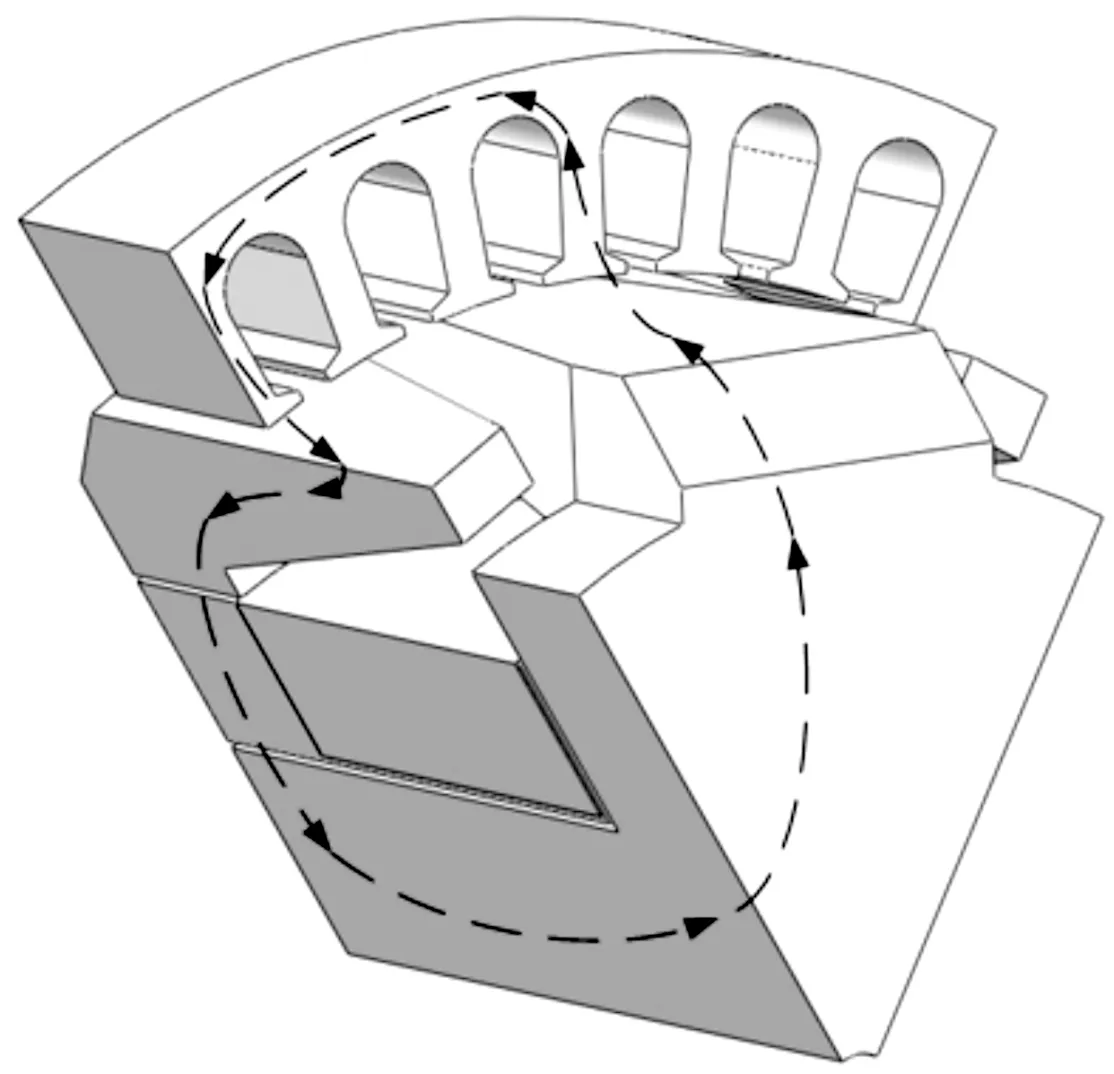
图1 爪极发电机的主磁路

3 爪极发电机的三维磁路构建

因为爪极形状的特殊结构，导致其气隙的有效区域与一般感应电机不同。并且其气隙磁密大小并不是均匀分布的，而是由爪根至爪尖气隙磁密逐渐减小。传统的磁路计算方法，往往只考虑到爪极磁路的有效区域，对于爪极电机气隙磁密的变化没有充分考虑，如果用传统的磁路法对爪极电机进行解析计算，因为不能准确的计算气隙磁密，会导致最后的计算结果误差偏大。本文中采用的三维磁路，不仅考虑了气隙有效面积的问题，同时也考虑到气隙磁密变化的问题，能够更准确的计算出电机各部分的磁通大小。

如图2所示，将气隙的有效面积在爪极上表示，可以得到图2(a)所示，将气隙部分按轴向长度等分为3部分，并将每一部分的气隙有效区域进行等效，等效后如图2(b)所示。等效后每部分的气隙面积与等效之前的面积相同，等分之后，可单独计算每一部分的气隙。按照气隙的等分方法，同样可以将每一气隙分段单元所对应的定子与转子部分进行剖分，其每一部分的的磁阻也分别进行计算。

图2 定子齿与转子爪极重叠面积

由于爪极电机的三维结构特点，该种电机中不仅存在径向磁通，同时也存在轴向磁通。由爪极电机的主磁路可知，爪极电机的轴向磁通主要存在于转子磁轭和转子爪极中，而其他部分只有径向磁通和切向磁通流过，基于这个特点，对于每一轴向分段单元内部，可只考虑其径向磁通与切向磁通，轴向分段单元之间，通过轴向磁阻进行连接。三维磁路的优点在于，由于每个磁阻只考虑其某一方向的磁通，所以会极大的简化其计算公式和计算过程，同时，由于每一轴向分段单元分别计算其轴向以及径向磁阻，使得计算准确性得到大大提高。

整个电机可以分为2个主要部分：定子及与定子对应的转子组成的部分和转子两端的端部部分。转子两端部分包括主磁路经过的两端附加气隙，转子励磁支架中参与主磁路的部分以及转子爪极极掌，这一部分磁路通过转子轭以及爪极极掌的轴向磁阻与电机主要部分连接。这一部分对于主磁路的影响不大，主要是起到构成闭合磁回路的作用。整个电机的轴向划分示意图如图3所示。其中，(a)和(e)为电机转子端部部分，(a)为前端部，(e)为后端部；(b)，(c)，(d)为电机定转子部分，(b)为定转子前端的轴向分段，(c)为定转子中段的轴向分段，(d)为定转子后端轴向分段。

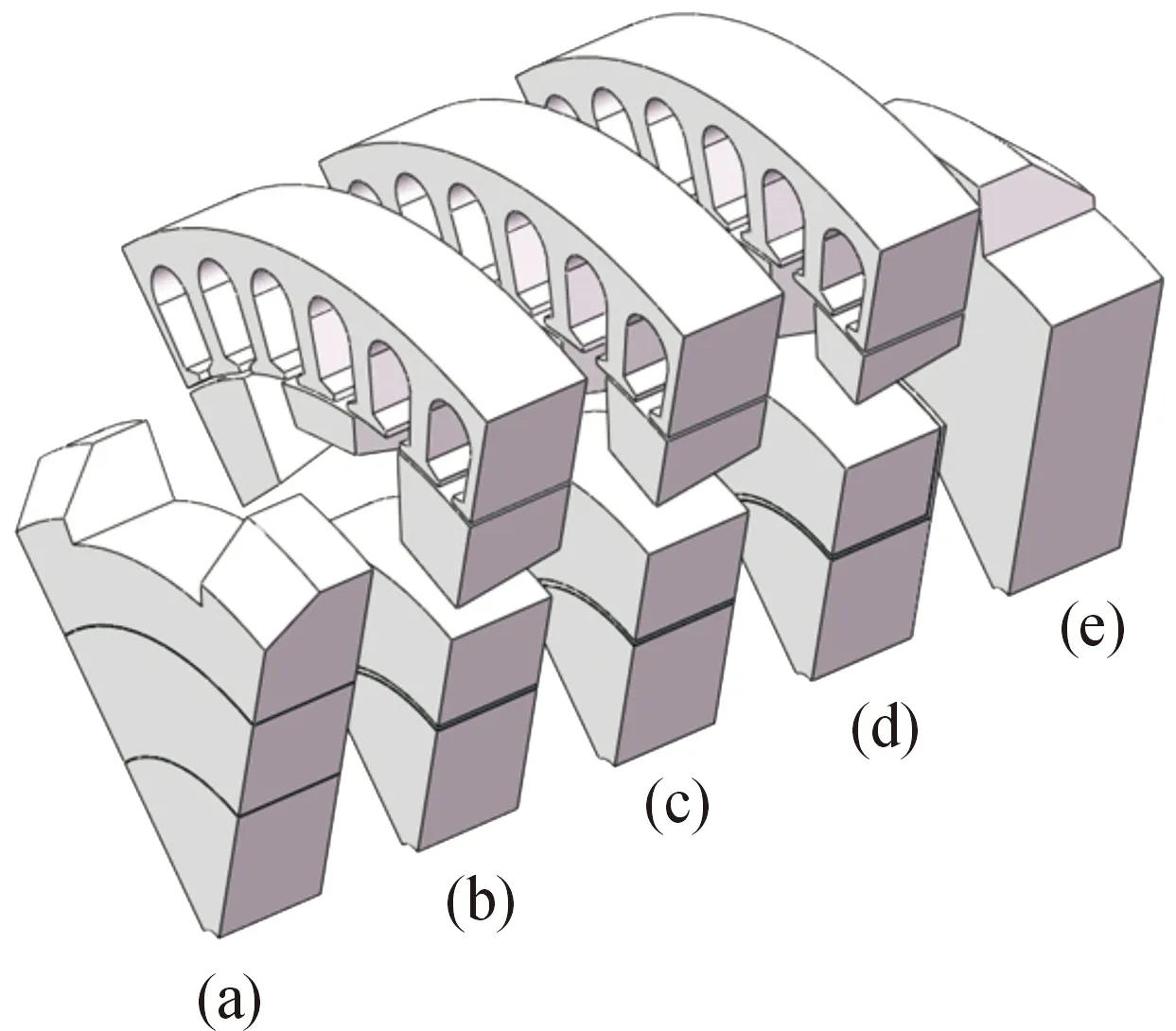
图3 爪极发电机轴向分段示意

每一剖分单元轴向划分部分通过定子与转子相对独立的构成径向的磁回路，并通过剖分单元之间的轴向磁阻连接，形成了整个爪极电机的三维磁路。

为简化计算，本文中只考虑电机一对极下的情况。通常，为把电机各部分磁场简化为相应的磁路，有以下几个简化的原则：(1)所划分的每段磁路为同一材料；(2)磁路的截面积大体相同；(3)流过该磁路各截面的磁通相同。(4)忽略饱和效应。

现对市面上一常见的电励磁爪极发电机进行分析，该电机主要设计参数见表1。

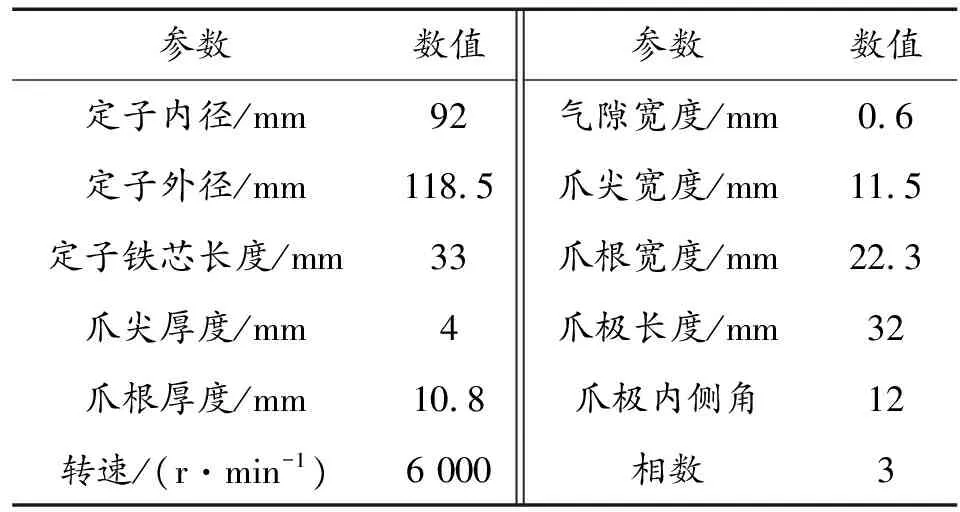
表1 电励磁爪极发电机参数

3.1 定转子主磁路的构建

定转子部分磁路作为磁路的主要部分，其对磁路的影响十分明显。将定转子部分沿轴向剖分为3部分，每一部分进行单独考虑。由于上文所提到爪极电机磁路的特殊性，在每一抛分部分内仅考虑径向的磁阻，在轴向分段单元之间，以轴向磁阻连接。

3.1.1定子部分磁路

定子铁芯的磁阻分为两部分，定子轭磁阻与定子齿部磁阻，其中仅存在单一方向的磁通，故定子铁芯的两部分磁阻仅考虑一个方向即可。

定子轭磁阻近似为一圆环体，因为只考虑一对极下的磁路，故其磁阻形状可等效为沿圆周方向等分为6份的圆环体。

(1)

其中：h为每一剖分部分的铁芯轴向长度；D1为电机直径；hs为定子齿高；μs为电机定子部分的磁导率；p为电机的极对数。

由于计算电机为平行齿，所以定子齿部磁阻可以将其近似看作一长方体，其磁阻公式如下：

(2)

其中：bts为定子齿计算宽度。

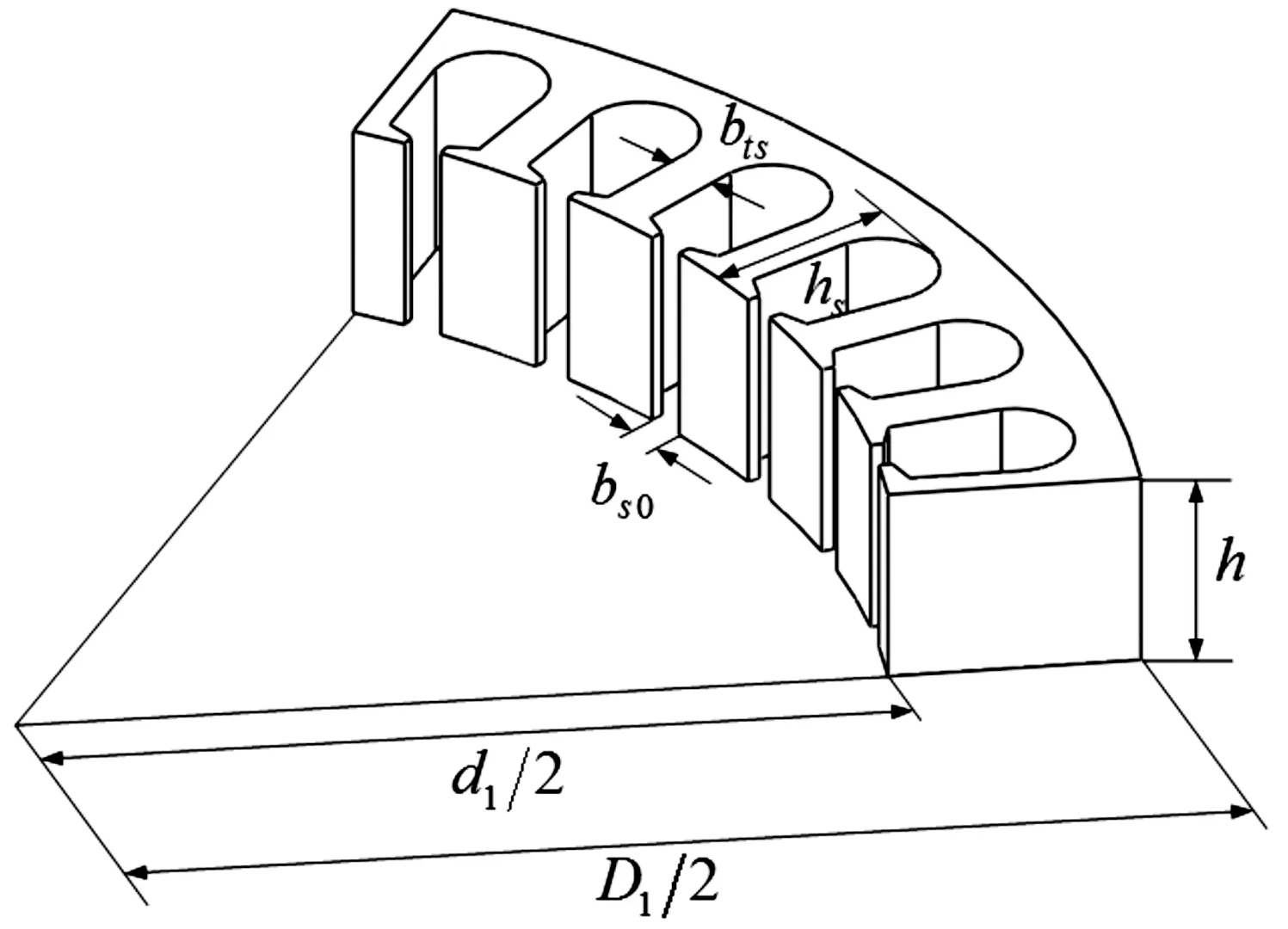
图4 定子分段单元结构参数

3.1.2主气隙磁阻

由于主磁通通过气隙进入定子齿部，所以在计算主气隙磁阻时，只需要计算转子爪极与定子齿的重叠面积即可。爪极部分可分成三段来考虑，将图3(a)阴影部分所示的气隙磁阻等效为如图3(b)所对应的气隙磁阻，每一段等效后的高度为爪极长度的三分之一，宽度为等效前所示梯形中线的宽度，等效之后可以得到一极下的气隙磁阻：

(3)

其中：hr为转子爪极的轴向长度；δ为气隙厚度；μ0为空气磁导率。等效长度lgn为轴向分段单元等效长度，其计算公式如下：

lgn=ln-2bs0,n=1,2,3

(4)

其中：bs0为定子槽口宽度；ln为每轴向分段单元的等效长度。其计算公式如下：

(5)

式中：θ为图3(a)中所示夹角；lp为爪极根部宽度。

3.1.3转子爪极磁阻

爪形磁极由于其形状的特殊性，其轴向，径向的磁阻是不同的。由于爪极从根部至爪尖截面积不断缩小，所以在将其沿轴向等分为三分时，每一部分将其等效成长方体，其轴向长度即为轴向分段单元的长度即hr/3，径向长度为等效的剖分单元中线的长度，等效后每个爪极单元的厚度为等效前梯形中线所在位置的厚度，下面给出每个剖分单元的轴向磁阻和径向磁阻：

轴向：

(6)

径向：

(7)

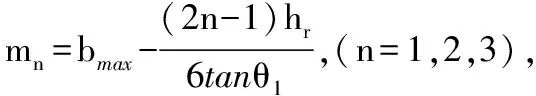
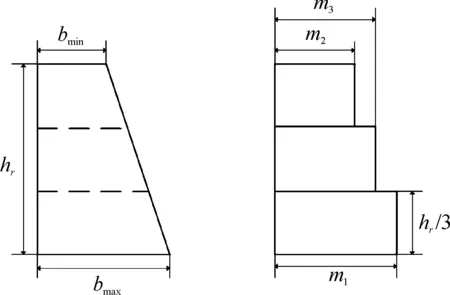
图5 爪极分段单元侧视

3.1.4转子轭轴向磁阻

转子轭部分磁阻计算较为简单，其每一剖分部分磁阻为：

(8)

其中：Rj1为转子轭内径；Rj2为转子轭的外径；μj为转子轭部分的磁导率。

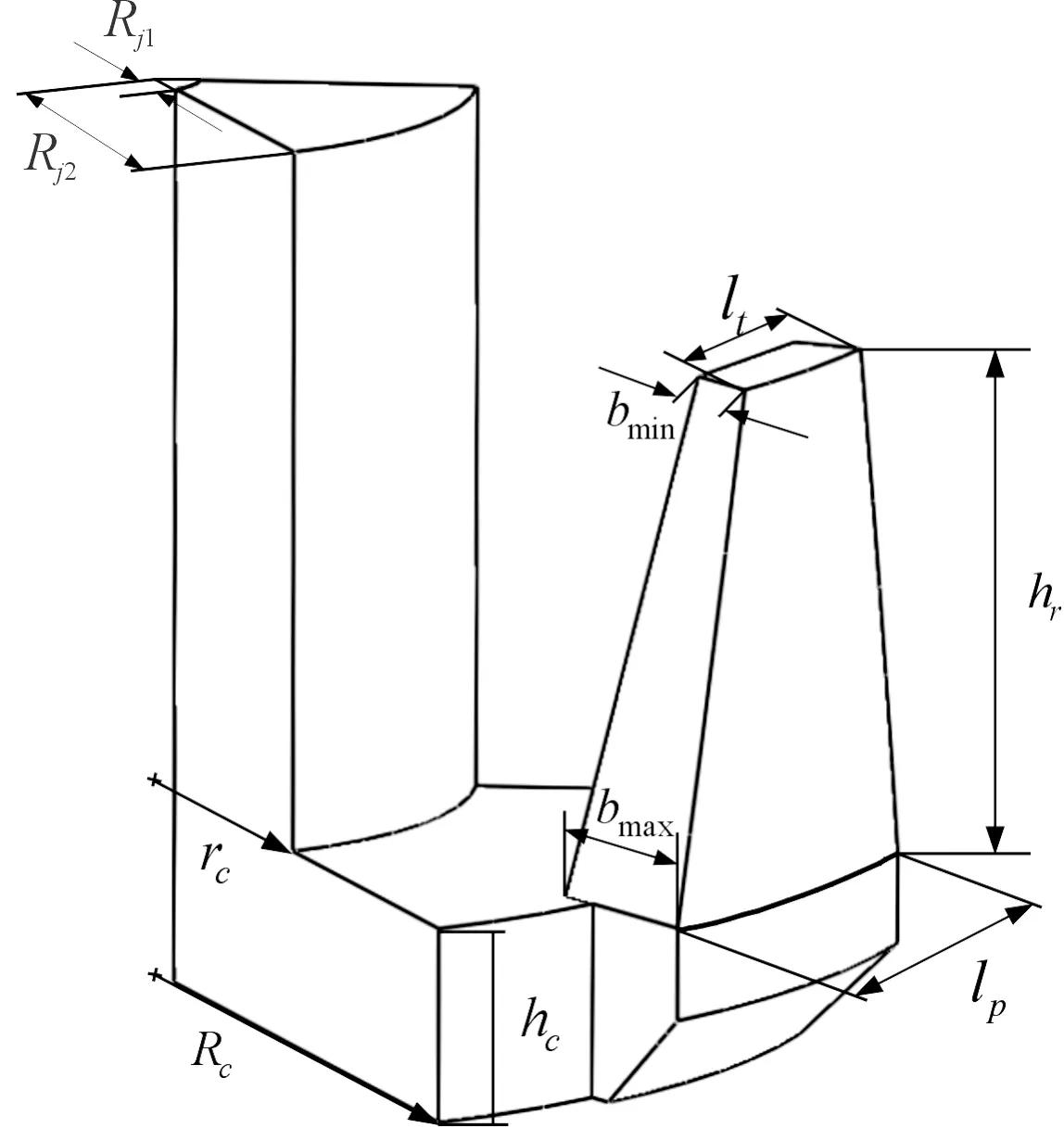
图6 爪极结构参数

3.1.5励磁磁动势以及电枢反应

本文研究电机的励磁方式为电励磁，由于是对该爪极电机一对极下的磁路进行研究，所以总的励磁磁动势为：

(9)

每极的电枢反应大小为：

(10)

其中：N为励磁线圈匝数；I为励磁电流大小；m为电机相数，取3；IN为额定电流有效值；Kdp为绕组系数，取1。

3.2 定转子内漏磁路

爪极电机的特殊三维结构，其漏磁路在整个磁路构成中所占的比例非常高，在设计较好的电机之中也往往达到40%～50%左右，除此之外，该电机的漏磁通的分量较多，种类也十分复杂。所以仅考虑主磁通，所得出的结果误差会十分大，漏磁通的作用也应该一并进行考虑。若将电机内全部漏磁种类都加以计算，将导致磁路过于繁琐，所以本文只考虑爪极发电机定转子内漏磁较为严重的几个部分，忽略漏磁小且计算较为复杂的部分。

通过研究可以发现，爪极发电机的漏磁主要集中在转子部分，由于前后爪极的磁极交错排布，且中间无隔磁部分，所以导致爪极发电机的极间漏磁较为严重。爪极转子内的漏磁可大致分为两部分，爪极转子内侧的漏磁通和爪极转子外侧的漏磁通，其中又以爪极内部的漏磁通较为严重，所以在分析时，应当着重考虑爪极内部的漏磁。

爪极转子的漏磁分为以下几个主要的分量，求出每一部分的漏磁阻，即可求出爪极电机漏磁通的绝大部分。

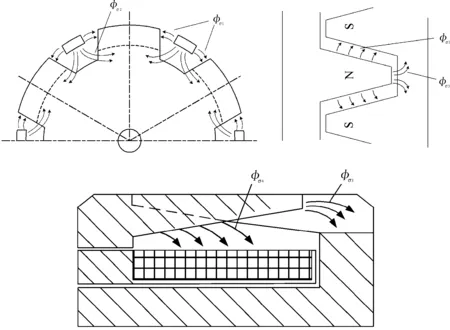
图7 爪极漏磁示意

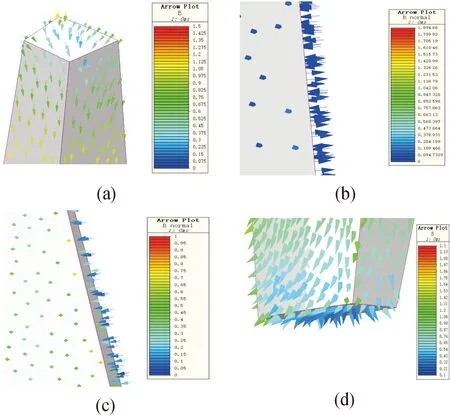
图8 4种漏磁分布

由于爪极电机的磁极排布成交错形式，2个相邻不同极性的爪形磁极之间会产生漏磁通。该漏磁的等效磁阻可表示为：

(11)

其中：τ为发电机极距；αp为电机的极弧系数。

该种漏磁存在于整个爪极的侧面，在电机每一个轴向分段单元中均有该种漏磁存在。

由于极性不同，爪极的内表面与极性相反的磁极板之间也会产生漏磁。该漏磁的等效磁阻可表示为：

(12)

其中：α为电机的分度角：lt为爪极尖部宽度。

该种漏磁分布在爪极极尖部分的内表面，所以仅在定转子两端考虑该种漏磁，在定转子中间部分忽略该种漏磁的影响。

在爪极极尖顶部同样会向另一极性的爪极板之间产生漏磁，其漏磁导大小与Λ1大小近似，其计算公式如下：

(13)

其中：lt为爪极尖部的宽度。

与转子极掌内表面漏磁类似，仅在定转子两端考虑该种漏磁。

前后爪极极性不同，所以与前爪极相连的转子磁轭与后爪极的内侧面之间会产生漏磁，其计算公式如下：

(14)

其中：d1为定子内径；β1为爪极内侧倾斜角。

该种漏磁分布在爪极的整个内侧面，所以在每个剖分部分均存在该种漏磁。

将上述磁阻以及磁势源按照爪极电机的主磁路流向以及定转子内漏磁路在电机中的分布情况，确定了爪极发电机定转子3部分的剖分磁路，如图9所示，其中，图中虚线内磁阻为定转子剖分部分的径向部分磁阻，虚线外侧磁阻为连接各个剖分单元的轴向磁阻。

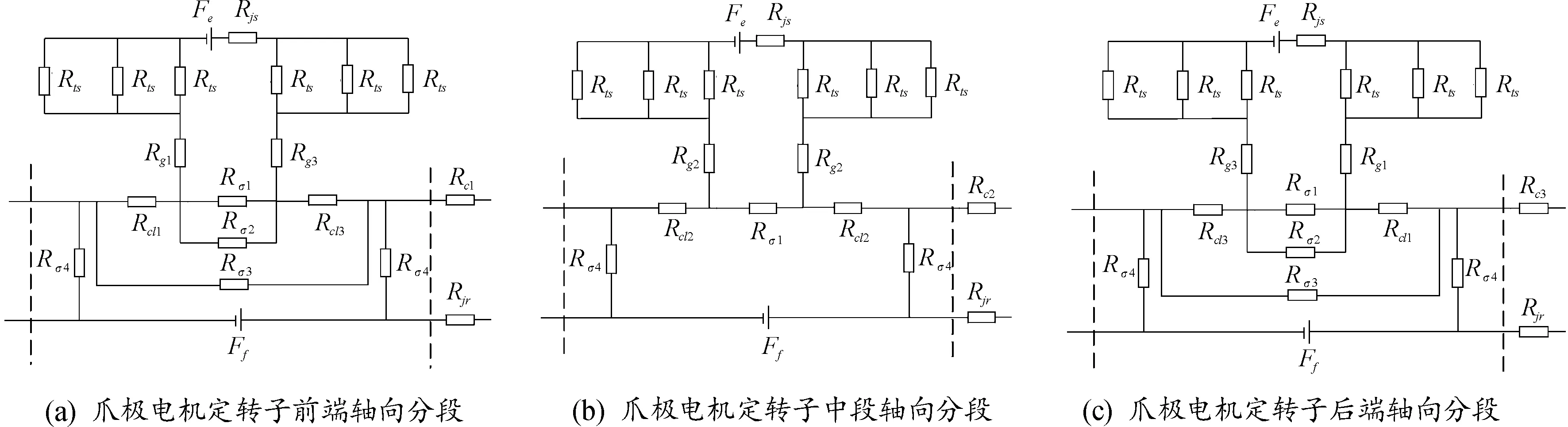
图9 爪极电机定转子剖分部分磁路

3.3 定转子外端部磁路

对于定转子外部的端部磁路，这一部分对于主磁路的影响不大，对磁路主要起到连接作用。在这一部分磁路中，附加气隙部分磁阻较大，在端部磁路占主要部分，如果计算不准确会导致最后的误差偏大。因此也应对这部分磁路进行考虑。

3.3.1端部附加气隙磁阻

主磁通通过励磁部分进入爪极的部分的附加气隙磁阻有两部分，一部分是励磁支架与转子轭之间的附加气隙，另一部分为爪极与励磁支架之间的附加气隙。两部分附加气息计算公式相同，其磁阻为：

(15)

其中：Rδ为附加气息的外径；rδ分别为附加气息的内径；hδ为附加气隙的轴向长度。

3.3.2励磁支架部分磁阻

励磁支架中仅底部在主磁路中，该部分可视为一扇环，其磁阻计算公式如下：

(16)

其中：Rz为励磁支架的外径；rz为励磁支架的内径；hz为励磁支架在主磁路中的轴向长度；μz为励磁支架部分的磁导率。

3.3.3爪极极掌部分磁阻

主磁通在爪极极掌部分方向发生变化，所以对于爪极极掌磁阻可分为轴向和径向来考虑。爪极极掌部分磁阻为：

轴向：

(17)

径向：

(18)

其中：Rc为爪极极掌的外径；rc为爪极极掌的内径；hc为极掌的轴向长度。

按照主磁路的流向将上述磁阻进行连接，可以得到爪极电机前端部和后端部的磁路，如图10所示。

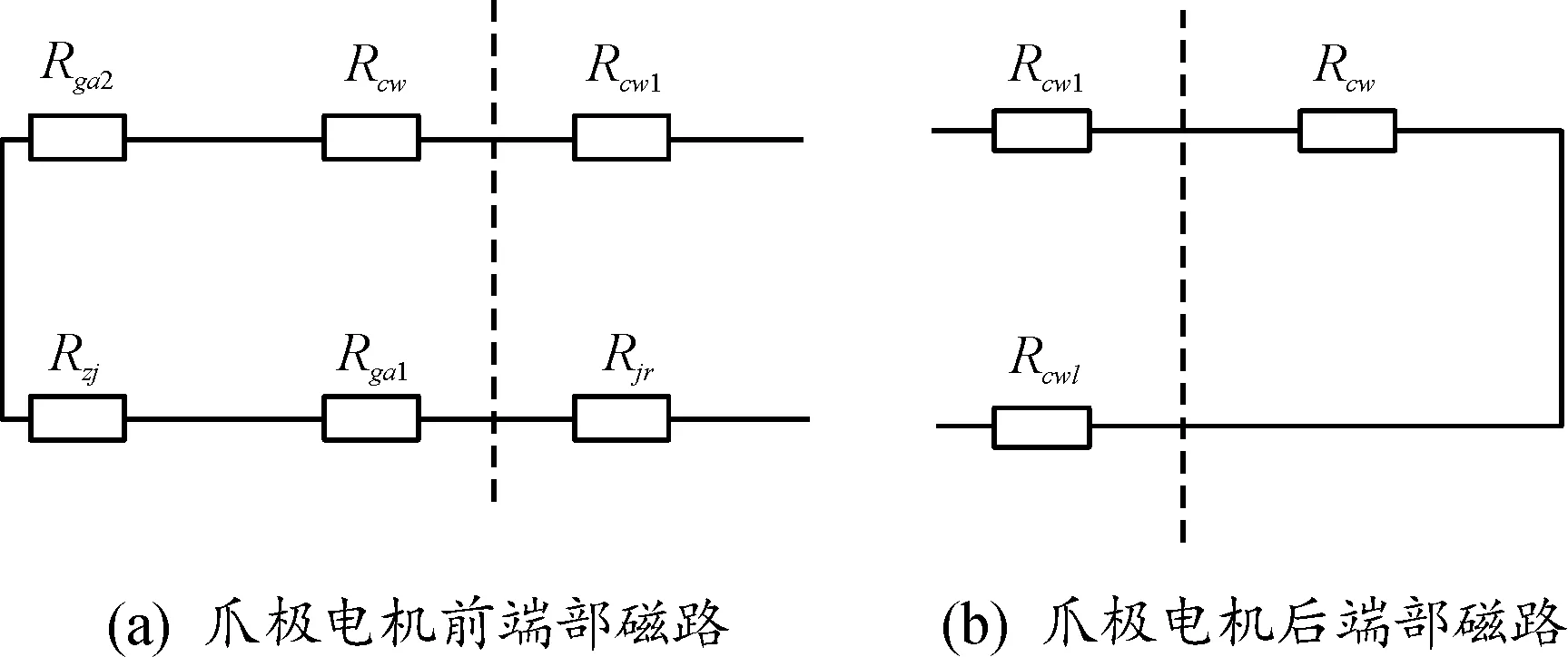
图10 爪极电机端部部分磁路

图10(a)中虚线左侧以及图10(b)中虚线右侧为径向磁阻，其余部分为轴向磁阻，通过轴向磁阻与定转子部分磁路连接。

根据以上各部分磁路的建立以及对电机结构和主磁通的分析，可以构建出电励磁爪极发电机的三维磁路如图11所示。

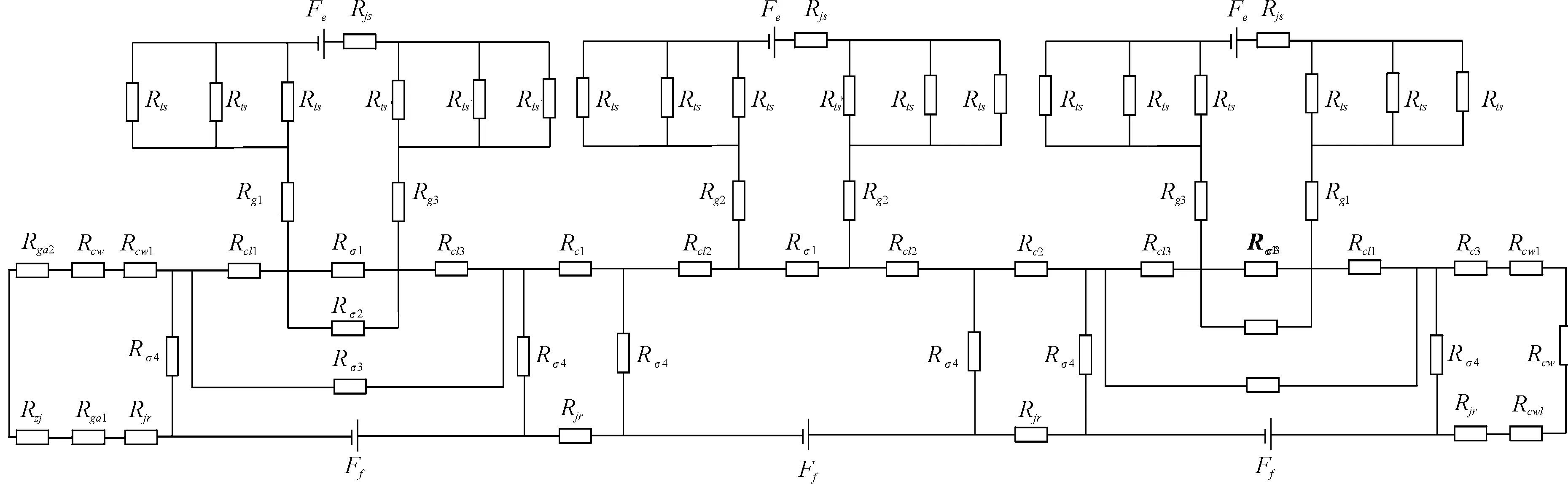
图11 爪极电机的三维磁路

根据磁路计算的模型，可以通过计算得出电机的主磁通φ，进而求得反电动势的有效值，计算公式为：

E0=4.44fφN1Kdp

(19)

其中：φ为穿过定子绕组磁通值；N1为定子内线圈匝数。

通过计算可以得到爪极发电机的等效磁路，以及各部分磁阻的数值，并通过相应的磁路计算求得每个磁阻中所对应的磁通数值。

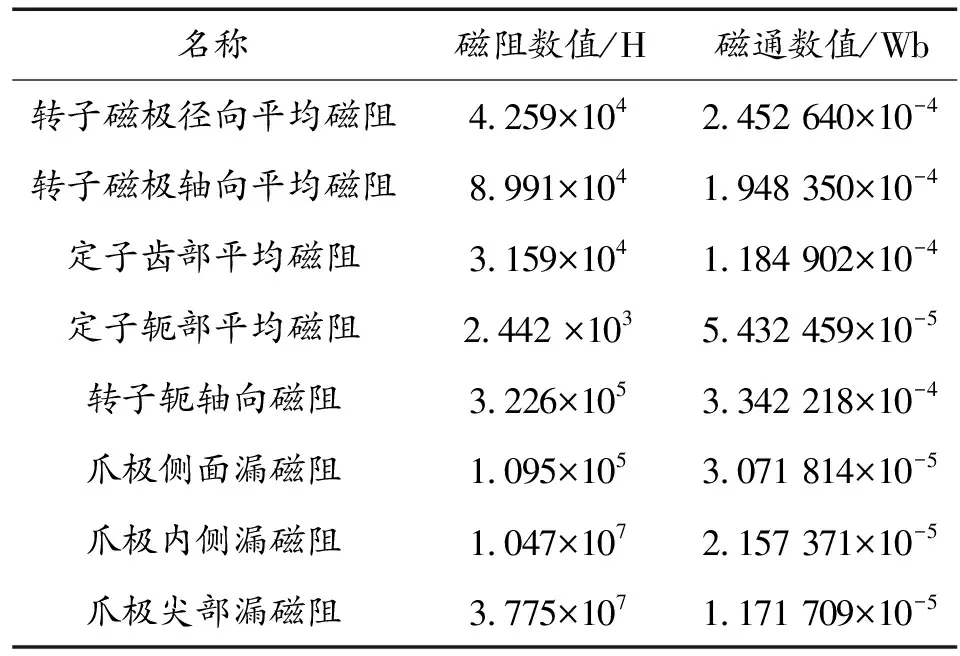
表2 磁路法磁通计算结果

4 三维有限元验证

为验证三维磁路的准确性，本文采用三维有限元计算结果作为参考，通过有限元计算，可以得到电机的磁密云图，并与磁路计算结果对比。

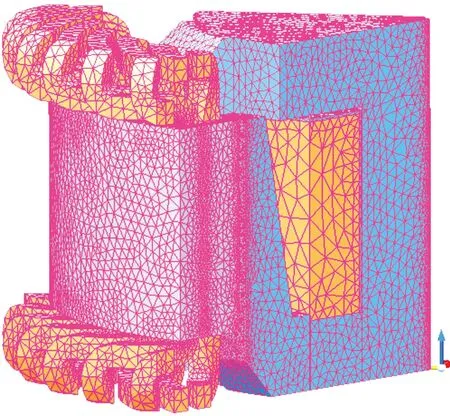
图12 爪极电机三维有限元网格划分

如表3所示，分别选择转子磁极表面磁密(图13中A所示位置)，转子轭轴向磁密(图13中B所示位置)，转子漏磁漏磁路磁密(图13中C，D所示位置)，以及定子齿部磁密作为参照，两者计算结果见表3。

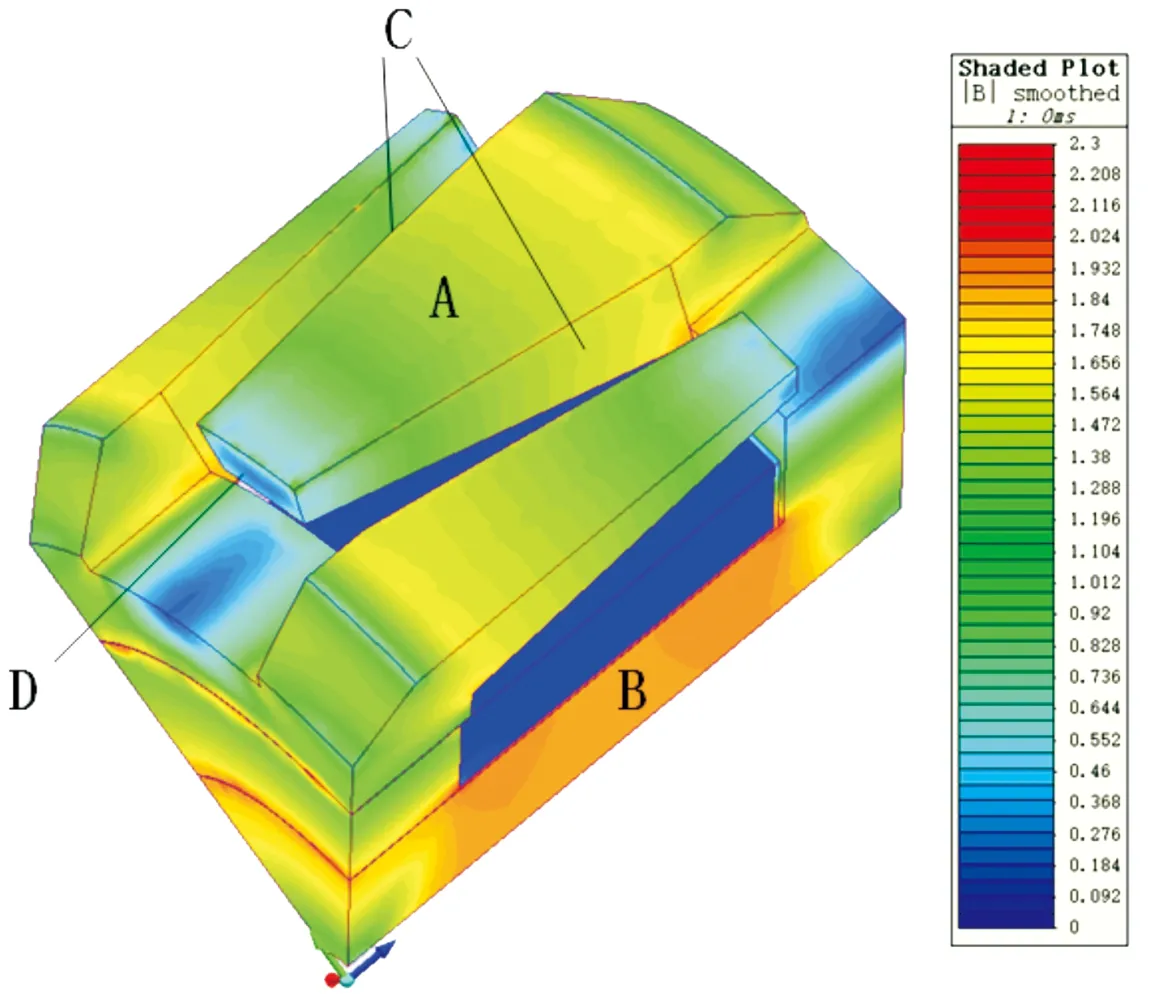
图13 爪极电机转子磁密云图

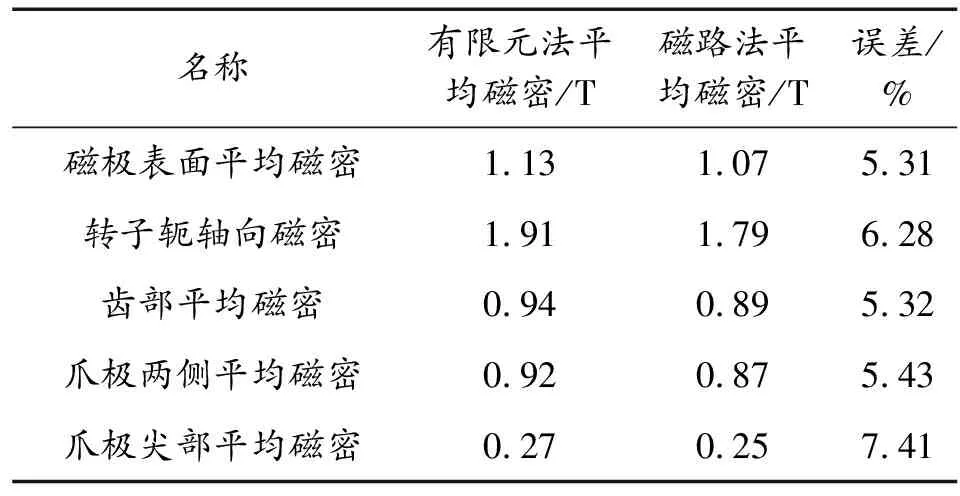
表3 有限元法与磁路法磁密计算结果对比

通过对比可以看出两者磁密的计算误差在可接受范围之内，基本可以满足工程设计的需要。出现误差的原因可能是因为对磁路中磁阻的等效以及忽略饱和效应所导致的。

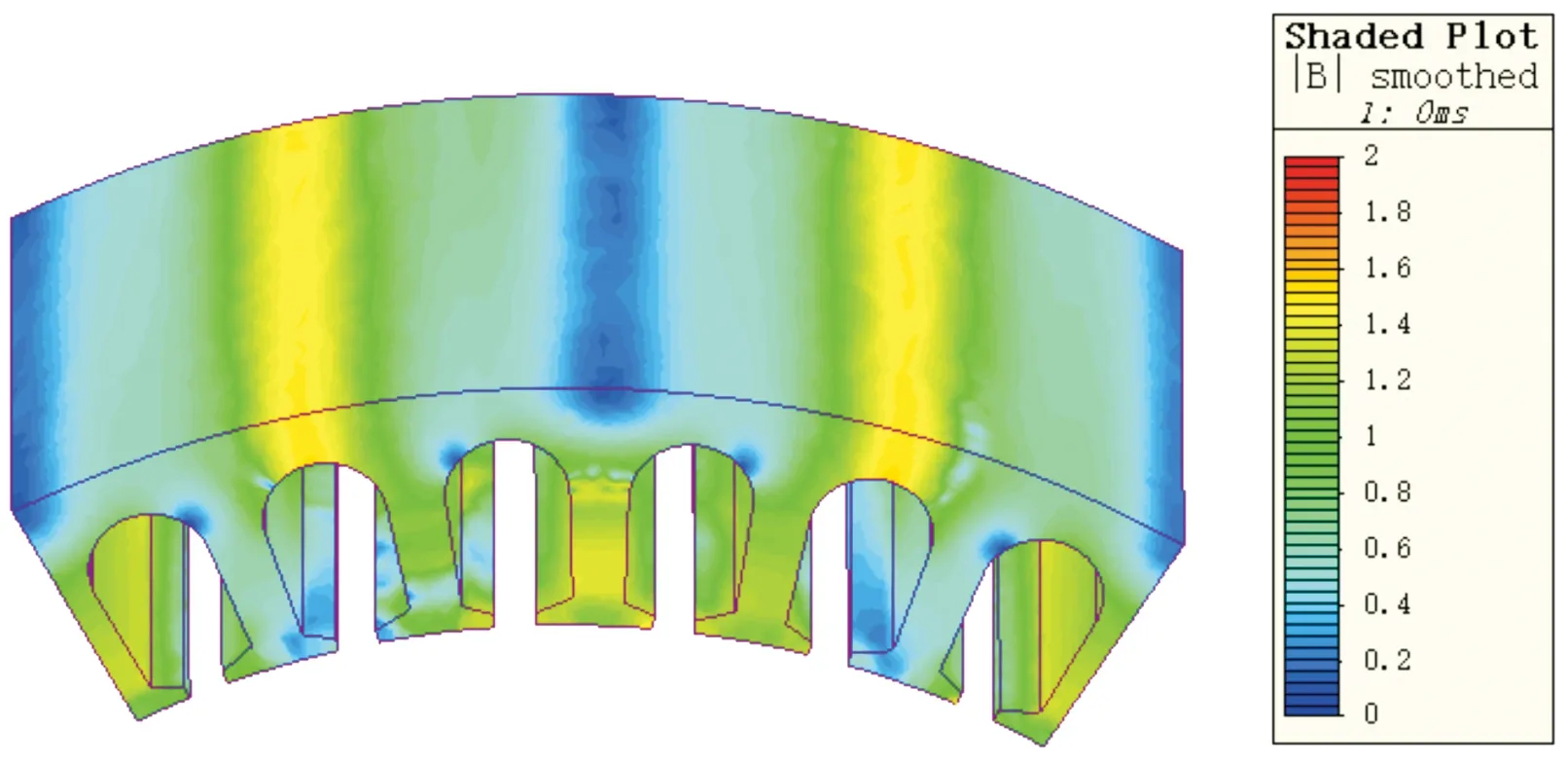
图14 爪极电机定子磁密云图

磁路计算得到的磁通值通过式(19)可进而得到每相反电动势基波波形，与三维有限元法基波对比可以得到如图15所示波形。经过计算，2种方法的误差极值在4.32%，在可接受范围之内。2种方法计算一致验证了三维磁路计算方法的准确性。

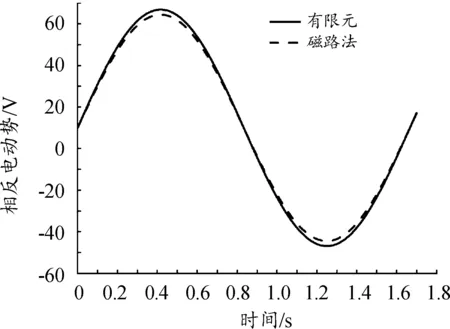
图15 爪极发电机相反电势基波波形

该电机采用星形连接，整流方式为全桥不控整流电路，通过计算可以得到爪极发电机的外特性曲线，2种方法的吻合程度较好。

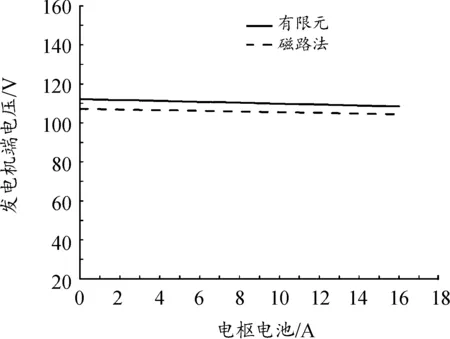
图16 爪极发电机外特性曲线

5 结论

本文中对电励磁爪极发电机的结构，主磁路，漏磁路等进行深入研究，得出简化等效的三维磁路模型，模型中各磁阻参数的解析推导，以及磁路构建方法，为研究该种电机提供了理论依据。

1)三维磁路法能够较为准确的计算出电励磁爪极发电机的主磁通数值，并通过反电动势计算公式得到爪极发电机的反电动势基波波形，其计算结果能与有限元法较好的吻合。

2)通过验证，本文中在计算磁阻的过程中运用的磁阻等效方法是可行的，误差在可接受范围之内，具有较好的准确性。

3)爪极发电机的漏磁种类多且占总磁通的比重较大，且在漏磁中占主要部分的是爪极转子内部的漏磁。本文推导出的漏磁导计算公式对后期该种电机的优化有借鉴意义。

综上，对比传统的磁路计算的方法，本文中提出的新型三维磁路法能够更快，更准确的对电励磁爪极发电机进行解析计算，为装甲车辆电机增容优化提供了一种较好的解析计算方法。