磁流变纳米复合材料减振器的磁路分析

胡志坚， 夏雷雷， 孙立志

(武汉理工大学 交通学院， 武汉 430063)

20世纪90年代学者开始对磁流变弹性体进行研究，磁流变弹性体是将微米级的铁离子均匀的分散在液态橡胶中，然后在磁场作用下固化得到，磁流变弹性体与磁流变液相比，不具有沉降稳定性的问题。21世纪开始随着纳米技术的发展，纳米材料得到了广泛的应用，很多学者将纳米材料混入磁流变弹性体中，使磁流变弹性体的力学性能得到大大改善[1-5]，因此磁流变纳米复合材料(Magnetorheological Nanocomposites, MRNCs)具有很大的应用前景。

在以往的研究中学者大多关注的是MRNCs的力学性能以及MRNCs减振器的力学性能，很少对MRNCs减振器的磁路进行研究，而MRNCs减振器磁路的设计又是MRNCs减振器设计的关键，决定了减振性能能否充分发挥。夏永强等[6-7]对磁流变弹性体隔振器进行了设计并对隔振器磁路进行了分析与仿真，但是没有给出线圈匝数的理论计算，赵灿等[8]在夏永强等的基础上对磁流变弹性体减振器进行了磁路分析，虽然给出了线圈匝数的理论计算值，但是与减振器磁路达到饱和时的总磁势计算不相符，两者所设计的磁流变弹性体减振器铁芯处最先达到磁饱和状态而不是磁流变弹性体处最先达到磁饱和状态。本文将对夏永强等设计的磁流变弹性体减振器进行结构改善，并且将磁流变弹性体换成耗能性能更好的MRNCs，通过理论与仿真的计算验证结构改善后磁路的优化情况，为MRNCs减振器的磁路设计及优化提供思路与方法。

1 MRNCs减振器结构设计

1.1 MRNCs的选择

本文采用Naimzad等[9]研制的MRNCs，该种材料具有较高的饱和磁感应强度，力学性能的改变范围也较大。该种材料由硅橡胶、纳米级的羰基铁离子、硅油、碳酸氢铵在各向同性条件下混合固化而成。材料的组成如表1所示。碳酸氢铵的作用是固化过程中分解成二氧化碳和水，使复合材料形成微孔，改善材料的力学性能。复合材料的B-H曲线如图1所示。

表1 多孔磁流变纳米复合材料的组成(质量分数)

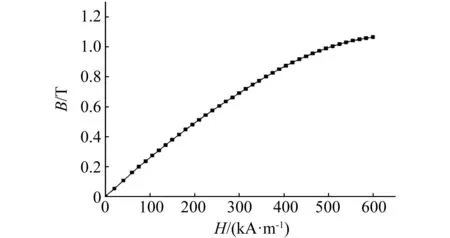
图1 MRNCs的B-H曲线Fig.1 The B-H curve of MRNCs

1.2 导磁材料的选择

所选导磁强度必须具有较高的饱和磁场强度，较大的磁导率，较高的性价比，且易于加工成型。因此选择DT4工业纯铁。其B-H曲线如图2所示。

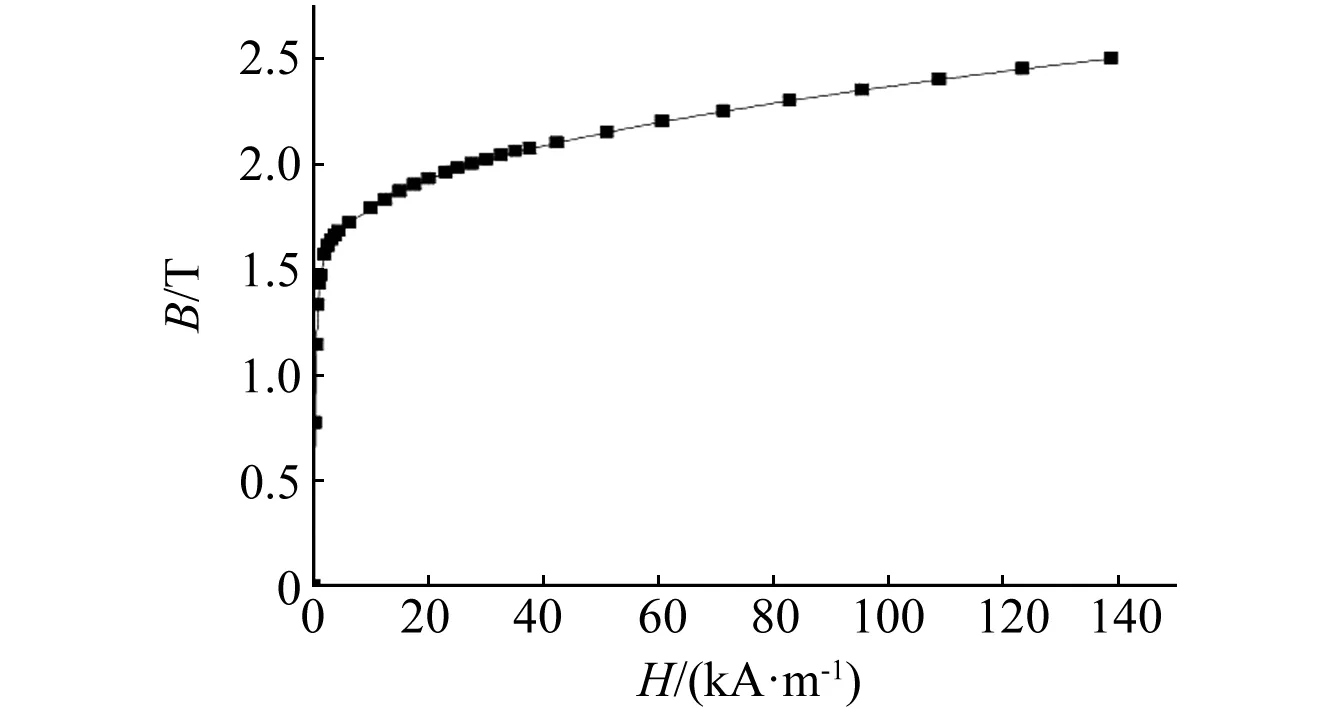
图2 DT4工业纯铁的B-H曲线Fig.2 The B-H curve of industrial pure iron DT4

1.3 MRNCs减振器磁路设计的一般步骤

对于一般的MRNCs减振器而言，磁路的设计主要考虑两方面因素：第一个因素是MRNCs处的磁场强度能否达到设计要求，这决定了MRNCs性能能否充分发挥;第二个因素是所需提供的线圈及通电电流能否满足结构布设的空间及材料要求。一般MRNCs减振器磁路设计流程如图3所示。其中调整结构尺寸主要是调整磁通面积从而调整磁饱和先后顺序同时调整了磁路饱和时磁通量的大小，调整时应以磁流变弹性体处先达到磁饱和为依据进行调整，从而更快的调整到满足设计要求。

1.4 减振器的结构尺寸设计

本次设计的减振器型式参照余淼等人所设计的隔振器结构型式，主要研究这种结构型式的MRNCs减振器磁路。减振器包括铁芯(直径为D1=10 mm，

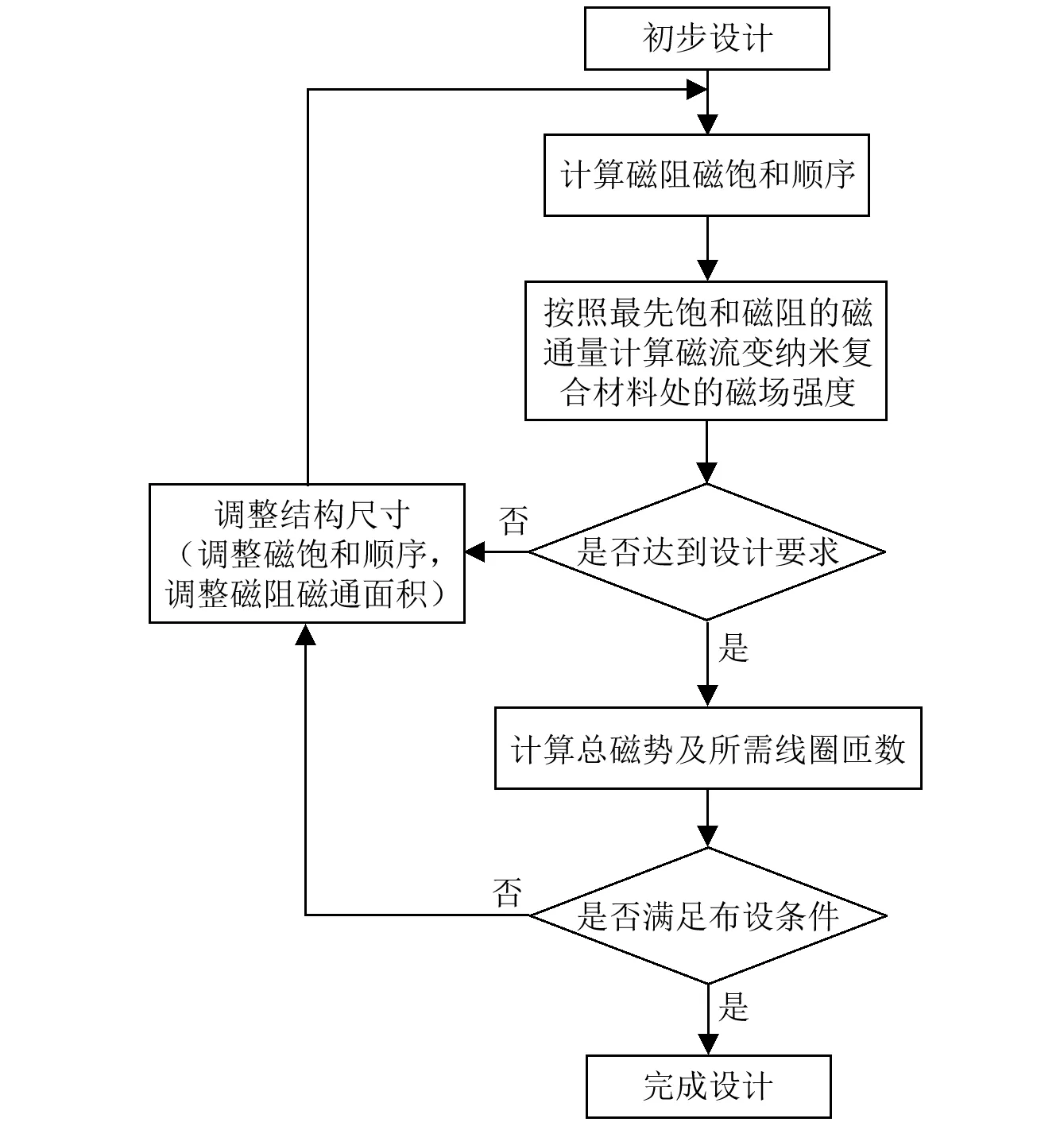
图3 MRNCs磁路设计流程图Fig.3 The flow chart of MRNCs magnetic circuit design

L1=40 mm)、上、下导磁体(直径D2=22 mm，h1=5 mm，h2=10 mm)、磁流变纳米复合材料(D3=32 mm，厚度a=5 mm)、套筒(D4=40 mm，厚度b=4 mm)、固定装置(不导磁的不锈钢材料)，整体结构图如图4所示。其工作原理为剪切模式如图5所示，即磁流变纳米复合材料受力方向与磁场方向垂直，材料受剪切作用。

图4 磁流变纳米复合材料减振器结构图Fig.4 The structure of MRNCs shock absorber

图5 磁流变纳米复合材料工作模式(剪切模式)Fig.5 The working mode of MRNCs (shear mode)

2 MRNCs减振器磁路分析与结构优化

2.1 磁路分析

选用的MRNCs减振器结构磁路的基本组成如表2所示。所设计的减振器磁路等效为串联电路如图6所示，本次设计忽略了漏磁效应。

表2 MRNCs磁路组成

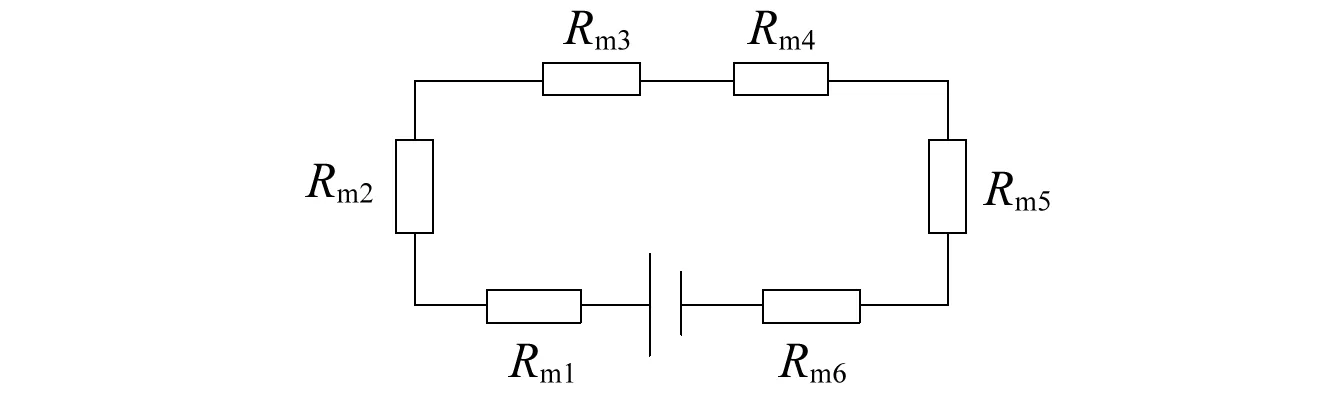
图6 磁流变纳米复合材料减振器等效磁路Fig.6 The equivalent magnetic circuit of MRNCS shock absorber

磁路的安培环路定理

∮Hdl=NI

(1)

式中：N为线圈的匝数;I为线圈中的电流大小;H为磁场强度。磁感应强度B与磁场强度H的关系为

B=u0urH

(2)

式中：u0为真空磁导率，其值为4πe-7Wb/A·m;ur为磁通路径的相对磁导率。

(3)

式中：u为磁通路径的磁导率，一般情况下u随着磁场强度的变化而变化。磁路的欧姆定律

(4)

式中：Φ为磁通;F为磁势;Rm为磁阻。并且有

Φ=∮BdS

(5)

F=NI

(6)

(7)

式中：B为通过面积S的磁感应强度;l为磁路平均长度。

在本次设计的磁流变纳米复合材料阻尼器的磁路中磁通Φ在磁路中处处相等，总磁阻Rm满足

(8)

由于各磁阻串联，应先计算出磁通量最先达到饱和状态的磁阻。磁路磁饱和计算结果如表3所示。

表3 初步设计磁路磁饱和计算结果

由计算可知按磁饱和先后顺序排列依次是铁芯，上MRNCs，上导磁体，下MRNCs，下导磁体，套筒。磁路按磁通量Φ=1.96(10-4Wb)计算出各磁阻对应的磁感应强度B的大小，再由材料的B-H曲线查出对应的磁场强度大小，并根据磁阻的长度计算出各磁阻对应的磁势，从而计算出磁路总磁势，计算如表4所示。

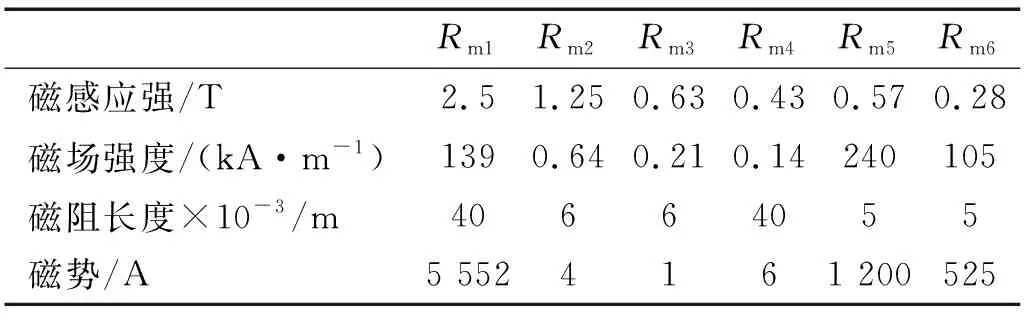
表4 初步设计磁路磁势计算结果

计算得总磁势F=7 288 A，选用直径为0.35 mm的漆包线，电流为2 A，计算线圈匝数N=7 288/2=3 644。由计算可知初步设计存在的问题有：①磁路铁芯处最先达到磁饱，并且MRNCs处磁场感应强度较小;②磁路总磁阻较大，所需布设线圈匝数过多。

2.2 MRNCs减振器结构优化

现调整结构尺寸，调整原则：第一，调整后减振器中磁流变纳米复合材料的性能能够充分发挥，即磁流变纳米复合材料处最先达到磁饱和状态;第二，调整后的减振器结构尺寸满足设计要求，性能达到使用要求。

经反复调整试算至满足要求：增大铁芯的磁通面积将D1=10 mm改为D1=16 mm，减小MRNCs的磁通面积将h2=10 mm改为h2=5 mm，从而L1=40 mm改为L1=45 mm。减小MRNCs的磁路长度，从而减小总磁势，将MRNCs厚度a=5 mm改为a=2 mm，从而D2=22 mm改为D2=28 mm，计算磁饱和顺序如表5所示。

表5 磁路改善后磁路磁饱和计算结果

此时磁饱和顺序为MRNCs，铁芯，上下磁极，套筒，满足我们所设计要求，磁路按磁通量Φ=4.40(10-4Wb)计算磁路磁势如表6所示。

表6 磁路改善后磁路磁势计算结果

计算得总磁势F=4 840 A，选用直径为0.35 mm的漆包线，电流为2 A，计算线圈匝数N=4 840/2=2 420匝。由计算可知，磁流变纳米复合材料处的磁感应强度变大，磁路总磁阻减小，所需线圈匝数减小，磁路得到改善，满足设计要求。

3 磁路结构的有限元分析

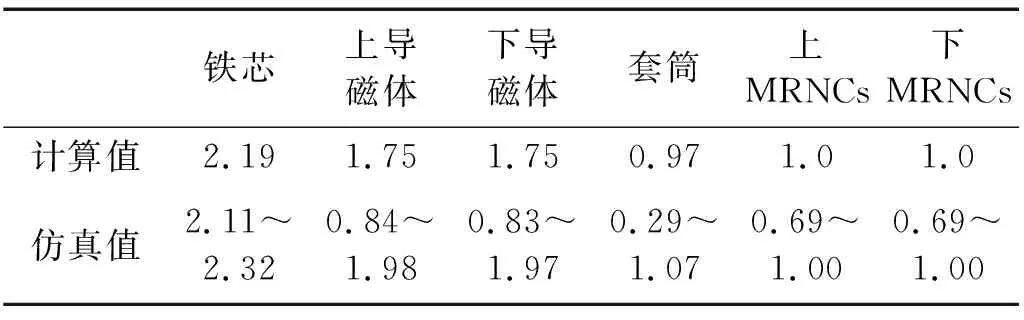
改善后结构磁感应强度计算结果如图7。减振器中磁场强度最大值出现在铁芯处为2.32 T。磁流变碳纳米复合材料处磁场强度范围在0.69～1.00内。结构改善后各磁阻磁感应强度计算值与仿真值,如表7所示。

(a)磁路各处

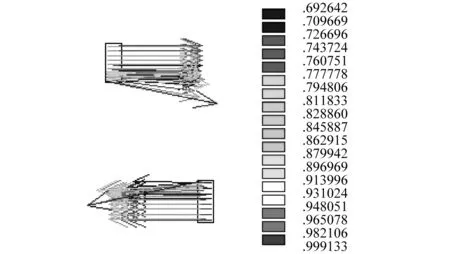
(b)MRNCs处图7 改善磁路后减振器ANSYS磁场强度计算结果Fig.7 The magnetic induction intensity results of improved design by ANSYS

T

表7计算值计算的是磁阻磁感应强度的平均值，而仿真值则是磁阻各处的磁感应强度值，是一个范围。由于铁芯接触面为上下磁极，材质相同；上下MRNCs处由于厚度很小；所以铁芯、上下MRNCs处仿真值变化范围不大。而上下导磁体和套筒与MRNCs连接处由于材料的磁化性能相差很大，所以接触面处磁感应强度最小，上下导磁体磁感应强度最大值在与铁芯接触处，磁场磁感应线开始从铁芯处向外扩张或者向铁芯处开始收缩。套筒内磁感应强度最大值发生在套筒中间部分，此时磁感应线最为集中。经过比较可得计算值与仿真值(各磁阻中部)磁感应强度值均相差不大，说明上述计算与仿真结果的正确性。

4 结 论

磁路设计是磁流变纳米复合材料减振器设计过程中必不可少的环节，磁路的设计决定了磁流变纳米复合材料减振器的性能。本文以一种典型磁流变弹性体减振器为例，将传统的磁流变弹性体换成性能更佳的MRNCs，对MRNCs减振器磁路进行了计算和改善并且对改善后磁路仿真分析，得出以下结论：

(1)提出了MRNCs减振器磁路设计的一般流程，对磁路进行了理论与仿真分析，为MRNCs在结构抗振中的运用设计提供思路，奠定基础。

(2)MRNCs减振器结构改善后磁路磁饱和顺序与参考结构相比，磁路的磁饱和顺序发生改变，由铁芯最先达到磁饱和状态改变为MRNCs处最先达到磁饱和状态。

(3)参考结构的磁流变弹性体饱和磁感应强度为0.7 T，结构改善后MRNCs饱和磁感应强度为1.0 T，工作区域磁感应强度提高42.86%。

(4)改善后MRNCs的用量相比参考结构磁流变弹性体用量减少了70.37%。

参 考 文 献

[ 1 ] LI Rui, SUN Lizhi. Magnetorheological smart nanocomposites and their viscoelastic behavior[C]// Society of Photo-Optical Instrumentation Engineers (SPIE) Conference Series. San Jose: SPIE, 2009.

[ 2 ] FELICIA L J, PHILIP J. Magnetorheological properties of a magnetic nanofluid with dispersed carbon nanotubes[J]. Physical Review E, 2014, 89(2): 758-761.

[ 3 ] NAIMZAD A, HOJJAT Y, GHODSI M. Porous and nonporous film-shaped magnetorheological nanocomposites: dielectric and electrical properties[M]. [S.l.] Smart Materials Research, 2014.

[ 4 ] YANG P, YU M, FU J. Ni-coated multi-walled carbon nanotubes enhanced the magnetorheological performance of magnetorheological gel[J]. Journal of Nanoparticle Research, 2016, 18(3): 1-11.

[ 5 ] WANG G, MA Y, DONG X, et al. Facile synthesis and magnetorheological properties of superparamagnetic CoFe2O4/GO nanocomposites[J].Applied Surface Science,2015, 357:2131-2135.

[ 6 ] 夏永强， 余淼， 刘胜龙. 磁流变弹性体隔振缓冲器设计及实验研究[J]. 振动与冲击， 2010, 29(9): 196-200.

XIA Yongqiang, YU Miao, LIU Shenglong. Design and experimental research of magnetorheological elastomers vibration isolation buffer[J]. Journal of Vibration and Shock, 2010, 29(9): 196-200.

[7] 余淼， 夏永强， 王四棋， 等. 磁流变弹性体的隔振缓冲器磁路分析[J]. 振动与冲击, 2011, 30(4): 47-50.

YU Miao, XIA Yongqiang, WANG Siqi, et al. Magnetic circuit analysis of an isolation buffer of magneto-rheological elastomer[J]. Journal of Vibration and Shock, 2011, 30(4): 47-50.

[ 8 ] 赵灿， 刘倩， 汤春瑞. 磁流变弹性体阻尼器的设计及磁路分析[J]. 机械与电子, 2013(12): 23-26.

ZHAO Can, LIU Qian, TANG Chunrui. Design and magnetic circuit analysis of magnetorheological elastomer damper[J]. Mechanical and Electronic, 2013(12): 23-26.

[ 9 ] NAIMZAD A, HOJJAT Y, GHODSI M. Comparative study on mechanical and magnetic properties of porous and nonporous film-shaped magnetorheological nanocomposites based on silicone rubber[Z]. 2014.