交直流配电网用模块化变换器模型预测控制
2023-02-09田二胜陈德志
侯 磊,刘 洋,田二胜,冯 毅,吴 杨,陈德志
(1.国网河北省电力有限公司 a.雄安新区供电公司;b.邢台供电公司,河北 保定 071000;2.许继电气股份有限公司 河北雄安许继电科综合能源技术有限公司,河北 保定 071000;3.国网宁夏电力有限公司 电力科学研究院,银川 750000;4.沈阳工业大学 电气工程学院,沈阳 110870)
与交流配电网相比,直流配电网在分布式能源接入、提高系统容量及效率、降低线路损耗及运行成本等方面具有显著的优势.如果将二者结合,将使中低压配电网技术更加灵活、可靠性更好.混合配电系统主要包括10 kV配电网、AD/DC变换器、DC/AC变换器、直流母线、DC/DC变换器、电动各类负载等,其中AD/DC变换器与DC/AC变换器采用的就是模块化多电平(MMC)变换器[1].
MMC需要同时对相电流、内部环流和子模块电容电压进行协调控制,因此,控制策略比较复杂[2-3].Angquist等[4]提出了一种基于参考输入和输出电压控制MMC的开环经典控制方法.MMC的环流抑制和保持电容电压平衡是控制难点,现有许多相应的文献对其进行研究[5-8].
在传统控制方法中,每个控制目标都对应着一个比例积分(PI)调节器,使参数调节更为复杂.然而,随着微处理器的发展,模型预测控制(MPC)被应用于电力电子和电力驱动领域[9].MPC可以消除PI控制器,省去了复杂的控制器设计过程.与传统控制方法相比,MPC由于具有动态响应快,易于包含非线性特性以及具有处理多个变量的能力[10-11],因此,引起了国内外学者对MMC控制的广泛关注[12].
本文提出一种交直流混合配电网的MMC子模块电容电压平衡MPC策略,对子模块电容电压平衡控制进行改进,减少了开关状态组合的数量,降低了计算复杂度.每次对目标函数进行滚动优化时,选择一个开通的子模块,并且根据输出电压电平的数量重复选择,以确定所有子模块的开关状态,可有效减少控制器的硬件及软件资源.在Matlab/Simulink软件中建立了仿真平台,对其进行了仿真分析,验证了所提方案的正确性.
1 MMC模型预测控制策略
1.1 MMC基本结构
图1所示为三相MMC拓扑结构.由图1可以看出,MMC由三个相单元组成,每个相单元可分为上、下两个桥臂(由下标u和l表示),与电感串联连接的N个子模块构成一个桥臂.Larm代表抑制环流的桥臂电感.MMC的交流侧与子模块(由两个IGBT(T1和T2)并联二极管和直流储能电容C构成)连接.当子模块被旁路时,其输出电压为零;当子模块被投入时,其输出电压为电容电压Uc.
1.2 MMC数学模型
根据图1所示的三相MMC拓扑结构建立其电压方程可得

图1 三相MMC电路拓扑结构
(1)
(2)
式中:j为MMC系统的a、b、c三个相单元;Uj为交流侧电压;Udc为直流侧电压;Uuj、Ulj分别为上、下臂电压的可控电压源.
通过建立三相MMC电压方程得到上、下桥臂电流为
(3)
(4)
式中:icirj为j相的环流;ij和idc分别为相电流和直流侧电流.
根据式(3)和(4)可知,内部不平衡电流、相电流与桥臂电流之间的关系式为
(5)
ij=iuj-ilj
(6)
式中,idiffj为内部不平衡电流.
由式(1)~(6)可得MMC系统的外部和内部动态特性方程为
(7)
(8)
利用前向欧拉公式,将Ts作为采样周期,对相电流和内部不平衡电压进行离散处理,得到离散时间模型分别为
(9)
idiffj(t+Ts)=B{Udc-[Ulj(t+Ts)+
Uuj(t+Ts)]}+idiffj(t)
(10)
(11)
式中:ij(t)为相电流的测量值;A=1/(A′/Ts+R);A′=L/2+L;B=Ts/2Larm.在理想条件下,MMC的交流侧有功功率和直流侧有功功率相等.
子模块投入和切除的电容电压预测值为
(12)
式中,im(t)=iuj(t)或ilj(t),为t时桥臂电流的测量值.根据式(9)、(10)和(12)可得MMC的目标函数为
(13)
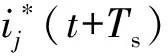
2 改进MMC模型预测控制策略
通过对MMC相电流、内部环流和子模块电容电压分别建立3个对应的控制器.MMC相电流目标函数表示为
(14)
MMC输出电压参考值可以表示为
(15)
式中,Slji和Suji为子模块的开关状态.
MMC上、下桥臂的电压参考值为
(16)
(17)
环流抑制由Udiffj的电平实现,即
(18)
因此,内部不平衡电流为
2Udiffj]}+idiffj(t)
(19)
内部不平衡电流目标函数为
(20)
对环流进行控制,上、下桥臂的参考电压变为
(21)
(22)
MMC子模块电容电压目标函数为
(23)
表1所示为使用不同方法每相子模块的开关状态组合数量.

表1 不同控制策略的开关状态组合数量
从表1中可以看出,本文提出的控制策略开关组合数量与文献[12]、文献[13]相比,开关组合数量减小一半,节约计算时间,即本文在不改变控制精度的前提下,可以有效节约一半以上计算时间.
3 改进MMC模型预测控制仿真分析
为了评估本文提出改进策略的性能,用Matlab/Simulink搭建了一个11电平的三相MMC仿真系统,仿真参数如表2所示,图2为策略控制流程图.
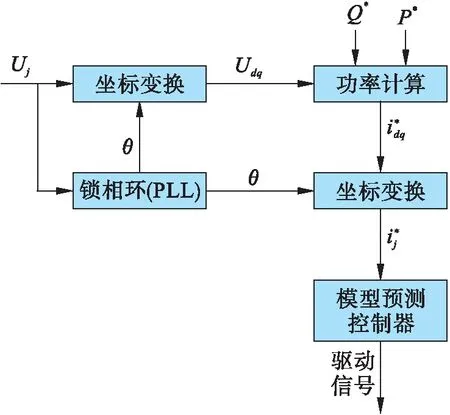
图2 MMC的模型预测控制流程

表2 仿真参数
交流系统送入MMC的有功和无功功率的表达式为
(24)
(25)
式中,id、iq和Ud、Uq分别为交流侧d-q电流和电压.交流侧电压已知,根据参考有功和无功功率计算d和q轴参考电流,然后,模型预测控制器根据参考电流计算出驱动信号对MMC进行控制.
MMC动态特性仿真结果如图3所示,有功和无功功率参考初始值设置为0.图3a为MMC的有功和无功功率的动态波形,可以看出MPC控制器具有很快的响应速度,动态性能良好;图3b和图3c为MMC的相电流和交流侧电压的波形;图3d和图3e为直流侧电流和上桥臂电流;图3f为a相的环流波形.

图3 改进MPC仿真结果
4 结 论
本文对直流混合中/低压配电网的中压侧交流变直流电力电子装置展开了研究工作,得到如下结论:
1)利用MMC相电流、环流和子模块电容电压建立目标函数,通过滚动优化选择最佳的开关状态组合,消除了权重系数,简化了传统控制策略.
2)模型减少了预测子模块开关状态组合,降低了算法的计算复杂度,并通过与其他控制策略进行运算量比较验证了其有效性.
3)通过在Matlab/Simulink环境中搭建11电平的MMC系统,验证了改进策略具有良好的稳态特性和动态特性.
