基于流固耦合的骨架膜结构优化
2023-02-09李延民赵树森王景玉
李延民,黄 瑞,赵树森,王景玉
(郑州大学 机械与动力工程学院,郑州 450001)
骨架膜结构是一种新型围护结构,预紧后的膜材与金属骨架整体构成一个高次超静定空间结构,依靠膜材与骨架整体形成的结构刚度来承受外部荷载,在力学上属于空间梁膜混合结构,具有典型的非线性特征.对比传统围护结构,具有结构简单、自重低、造型多样、抗震性能优良的特点,其制造规格统一,多为工厂化生产后现场拼装,便于快速搭建一个大跨度无支撑结构,能提供更大的有效空间[1].广泛应用于工业、建筑、国防等领域中作为设备、仪器、建筑的围护结构[2].
骨架膜结构在服役生命周期中暴露于自然环境下,受多种环境荷载的影响,其中最为严重且最不规律的是风荷载[3].因此,有必要对此类围护结构进行风场分析,目前,该类结构设计时多按照相应规范取单一风向角(0°风向角)下的风压分布进行设计验算,不能反映出实际的最恶劣工况.
刘奕等[4]采用风洞测压试验对不同地貌下不同深宽比的矩形高层建筑进行了风荷载及其周身绕流特性的研究,得到了矩形高层建筑表面的一些风压分布规律;李志国等[5]基于风洞试验对某机场航站楼的大跨度曲面屋盖的脉动风荷载分布进行了研究,得出屋盖迎风前缘及部分曲面弧度变化大的位置处风荷载在不同风向角下呈现非高斯特性.但由于风洞试验费用高、周期长,较少对膜结构进行全尺寸的风洞试验,而缩尺模型由于雷诺系数的不同,其风场往往与实际风场有差别.Amaya-Gallardo、Amini、方智远等[6-8]采用数值模拟的方法,与实尺模型场地实测数据、风洞试验数据对比,证明数值模拟方法得到的建筑物表面平均风压能较好地与场地实测数据、风洞试验数据吻合.
现阶段,国内外虽存在一些学者对低矮类建筑结构或膜结构的风场特性进行研究,但多将建筑结构本身视为刚性体,忽略了其本身在风荷载作用下的结构变形对其表面风压分布的影响.流固耦合的相关概念虽然提出得很早,但是其对计算机的性能要求很高,限于早期计算机的性能,基于双向流固耦合的风场特性研究鲜有报道.目前,随着科学技术的发展,采用弱流固耦合计算的门槛已经降低.本文基于ANSYS,考虑了膜结构在风荷载作用下的结构变形对建筑表面风压分布的影响,采用双向流固弱耦合,对低矮类膜建筑的风场特性与骨架膜结构风致结构受力进行了分析研究.同时,骨架膜结构的优化一般通过优化杆件的截面尺寸来实现轻量化设计,但未考虑其设计荷载与实际荷载之间的差异.本文基于流固耦合所得到的多个风向角下建筑表面的风压分布数据,对该建筑的立面骨架膜结构进行了轻量优化,相比减重14.73%,有效节约了原材料.
1 双向流固耦合分析流程
针对此类对风荷载较为敏感的结构,采用双向流固耦合分析与实际工况更为接近,与单向耦合分析不同的是,在需要耦合的流场计算表面区域创建动网格.将CFD求解器解出的耦合面风压分布与FEM求解器解出的结构位移量,通过System Coupling模块在每个时间步间互相交换作为各自输入变量再进行下一个时间步的求解,依次循环,实现双向流固耦合,这样大大减少了将流场N-S方程与动力学方程联合求解的巨大工作量且保证了求解的准确性,其求解流程如图1所示.

图1 双向流固耦合分析的一般流程
2 风场分析
2.1 分析模型建立
该骨架膜围护结构安装示意图如图2所示(单位:mm).该结构总长80 m、宽30 m、高12 m,屋盖坡度为15°;屋面设有4面整体框架均布平面骨架膜结构,长35 m、宽10 m,立墙上设有16面框架均布骨架膜结构,长10 m、宽6 m.为了便于模块化制造与包装运输,将骨架膜结构设计为均匀大小,其中屋面骨架膜模块尺寸为3 m×2 m、立面骨架膜模块尺寸为2 m×1.5 m.
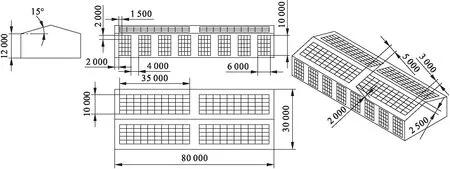
图2 骨架膜结构安装示意图
相关调查研究表明,低矮类建筑在强风下,屋面与一些围护结构处会产生局部低气压,在内外压强差的作用下导致建筑物的围护结构受损[9-10].因此有必要对不同迎风角下建筑表面的风压分布进行研究,确定最危险的迎风角度.
2.2 计算域与网格模型
由于实际湍流场的参数分布规律难以获得,本文使用充分发展的流场去模拟真实入口边界条件,为了保证流场的充分发展,需要确定一个足够大的流场区域,在风向角为0°(与YOZ平面夹角)的情况下,流场计算区域大小为600 m×448 m×240 m,流场入口距离建筑180 m,出口距离建筑后边缘390 m[11].图3为流场网格模型.采用分区组合的方式离散流场,远离建筑的外区域采用六面体结构化网格.考虑到湍流区域空气流向变化剧烈,在内区域采用非结构化的四面体网格,并在建筑周围进行局部加密.整个计算流场网格模型共1 300 257个节点、2 891 472个单元.
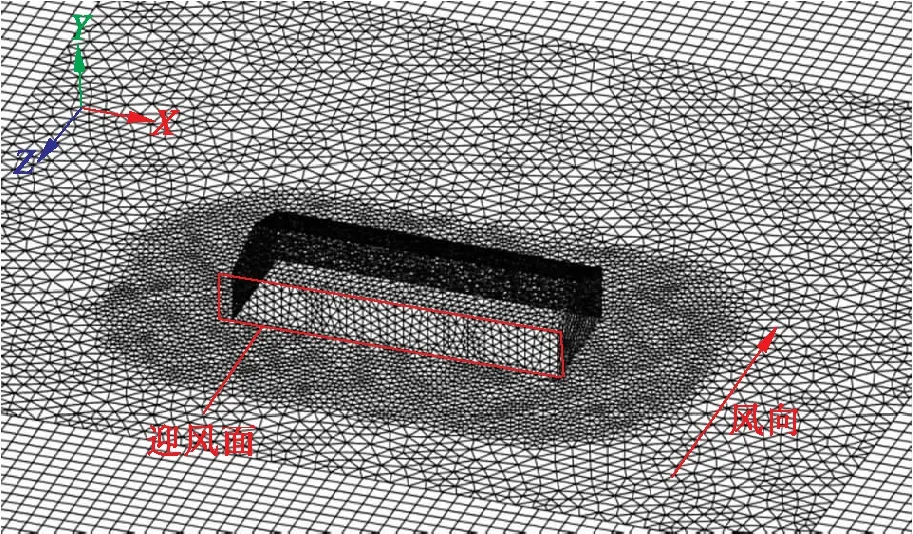
图3 流场网格模型
2.3 流场边界条件
在Fluent中将湍流模型设定为k-εRNG模型,将入口的均匀流与实际湍流场建立联系.根据统计,上海市50年重现期基本风速为31 m/s,因此入口风速设置为31 m/s,出风口压力为标准大气压[12].近壁面处理方式为Standard Wall Functions;材料假定为不可压缩粘性空气,质量密度取1.225 kg/m3,粘度为1.789 4×10-5kg/m·s.
对于一个充分发展的流场模型,其湍流特性可以采用湍流强度I与湍流尺度l描述,湍流强度主要靠雷诺数Re估算,而湍流尺度与流场中对流动影响最大的因素有关,此处为建筑来流方向特征尺度,表达式为
(1)
I=0.16(Re)-1/8
(2)
l=0.07L
(3)
式中:ρ为流体密度;μ为流体动力粘度;u为流速;L为建筑来流方向特征尺度.将式(1)、(2)联立得到湍流强度I=1.69%,由式(3)得到湍流尺度l=2.1 m.
3 风场数值模拟结果与验证
3.1 风场数值模拟结果
通过仿真得到的0°风向角下的风场压力分布如图4~6所示.图4为距建筑侧墙5 m处剖面的风速矢量图,可见由于气流流向存在截面大小的剧烈变化,在迎风面方向屋檐与屋脊位置出现了明显的气流分离现象,导致局部产生了高负压,而背风面由于建筑阻挡形成负压,引起周围空气的回流,形成涡流致使背风面呈现局部正风压.由图5可见,计算区域囊括了整个受建筑物阻碍所形成的湍流区域,说明流场的大小满足计算需求.由图6可见,整个建筑迎风面受到来流撞击产生正压作用,其余区域均为风负压作用.

图4 风速矢量图
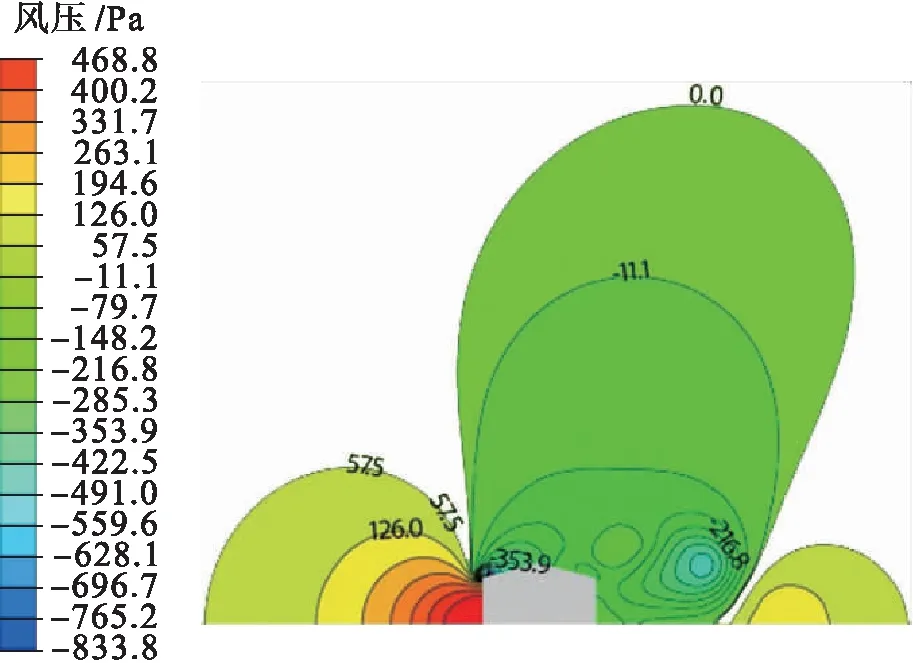
图5 中轴线截面风压分布

图6 建筑表面风压分布图
为了方便对比,将仿真得到的风压分布数据以不受建筑物影响的远高处风压作为参考值进行无量纲化,得到平均风压系数表达式为
(4)
式中:Q为建筑表面任意位置的风压;QH为远高处的静压;VH为平均风速.
图7为建筑物屋面风压系数分布等高线图.
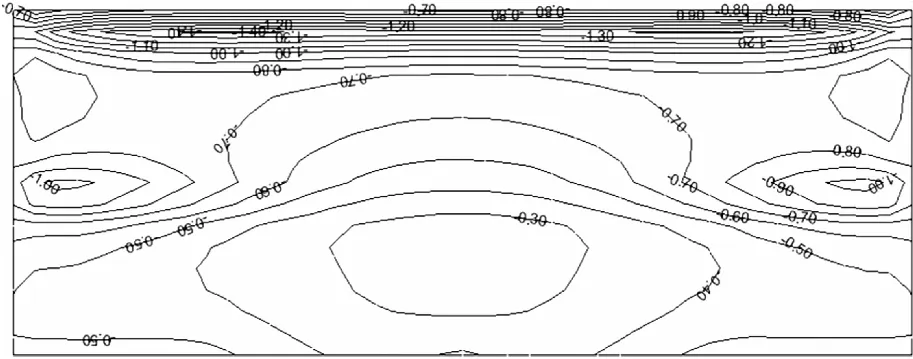
图7 风压系数分布等高线图
3.2 结果验证
为了验证仿真得到的风压数据是否有效,选取同类型低矮建筑模型TTU(美国德州理工大学)实尺模型场地实测数据[13](见图8,单位:mm)、同济大学风洞试验数据[14]和建筑结构载荷规范(GB 50009-2012)中给出的低矮双坡屋面建筑(坡度为15°)的风压分布体系系数参考值,与建筑物模型中轴线上分布的测点处测得的风压系数相比较,得到的对比曲线如图9所示,测点位置排序按图中A→B→C→D→E的方向散布.

图8 TTU模型及测点布置图
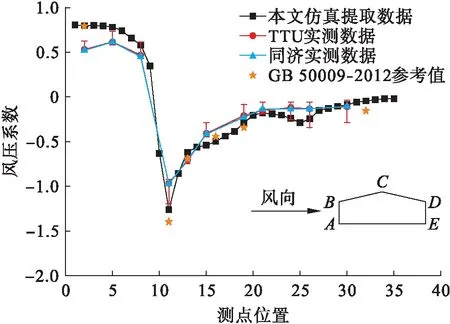
图9 建筑物中轴线分布测点风压系数对比
由对比结果可知,数值模拟结果与实测数据、风洞试验数据具有相似的趋势,与国标参考值吻合度较高,由于本文的建筑模型与TTU、同济大学所采用的模型在尺寸和屋面坡度不同,故在迎风面、屋檐、屋脊处的风压系数分布有一定的不同,总体而言,所得风压数据合理准确,能够满足工程应用的需要.
类似的,改变风向角为45°、90°并设置对应的计算域大小和湍流参数,其余边界条件保持不变,得到了45°与90°风向角下该建筑的表面风压分布,如图10所示.

图10 45°、90°风向角下建筑物表面风压分布图
4 骨架膜结构风致结构受力分析
4.1 骨架膜结构几何模型
本文以立面骨架膜结构为例,介绍该结构的流固耦合仿真与优化过程.骨架膜结构整体由膜材、上弦杆、腹杆、下弦杆、节点支撑杆与连接节点构成,整体受力分析时将该膜材简化为shell181膜单元,上弦杆件简化为beam188梁单元,腹杆、下弦杆与节点支撑杆简化为只受拉压的二力杆link180单元,为方便叙述,文中使用“二力杆”代指这些杆件[15].简化后的模型如图11所示.

图11 骨架膜结构简化模型
上弦杆是型号为8/5的角钢,厚5 mm,腹杆与下弦杆采用截面为φ50×10 mm的钢管,节点支撑杆是截面为φ60×10 mm的钢管,金属骨架的材质均为Q235,膜材厚度为0.8 mm,材质是型号为G7的PTFE膜材.
4.2 边界条件
在Mechanical模块中将膜面单元使用APDL命令施加6 kN/m的预张力,打开大挠曲开关,施加重力荷载,将膜面设置为流固耦合面,将膜结构的固定约束按照实际情况在上弦边杆施加固定约束,在下弦支撑节点处施加不动铰支座.离散后的屋盖骨架膜结构节点总数为45 270,单元总数为41 674;立面骨架膜结构节点总数为28 661,单元总数为27 005.
4.3 仿真结果
在0°、45°、90°风向角下对立面骨架膜结构进行流固耦合仿真.图12为骨架膜结构在不同风向角下的变形图.表1为立面骨架膜仿真结果.

表1 立面骨架膜仿真结果

图12 立面骨架膜结构在不同风向角下的变形图
4.4 结果分析
由仿真结果可知,立面骨架膜结构在0°与45°风向角下承受的风荷载为正风压,而在90°风向角下承受的为负风压;在90°风向角下膜面变形的应力、骨架最大挠曲、受拉的二力杆最大轴力与杆件所受最大拉应力均比0°与45°风向角工况下大,但受压的二力杆轴力与杆件所受最大压应力却产生于0°风向角下.其中,骨架最大挠曲位置为正中间的下弦杆中心,最大拉杆与最大压杆均为两侧中间位置铰支座处的四根斜腹杆,杆件所受的最大组合拉压应力分别处于与该斜腹杆相连的上弦杆的上下翼缘处.膜面的最大应力差别不大,均远低于膜材的极限抗拉强度标准值160 MPa.
在不同风向角下,风场的小范围高负压区域可能导致骨架膜围护结构局部产生较大的变形挠曲、轴力和应力.从骨架膜结构在不同风向下结构受力情况来看,最大受力杆件为与支座铰接的斜腹杆,其次是下弦杆,而骨架中间部位的腹杆总体受力较小,因此,可以考虑对这三种杆件使用不同截面尺寸的钢管制造以轻量化整个结构.
5 骨架膜结构优化
在结构设计中,常采用响应面法对结构的相关设计参数进行优化,通过对大量样本点进行计算,拟合出设计变量与目标变量之间的响应函数,并在给定的约束条件下挑选出最符合目标函数的候选点,将候选点圆整成制造值得到最终优化参数.一般优化流程如图13所示.
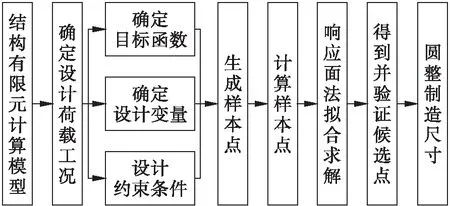
图13 响应面法的一般流程
根据建筑结构载荷规范对骨架膜结构取不同承载力极限状态组合进行对比,其中风荷载采用仿真得到的不同风向角下骨架膜结构表面压力分布数据,其余荷载按规范取值.根据对比可知,对结构整体承载最不利的荷载工况为:1.2D(恒载)-1.4W(90°风向角下负压风载)+1.0F(膜面预应力)-0.7T(降温)的组合.
以该极限工况组合作为施加荷载,使用ANSYS Workbench中的优化设计模块对该骨架膜结构的金属骨架进行截面尺寸优化,输入参数为杆件的截面尺寸,其值取常用的角钢、圆钢管截面尺寸,输出参数为结构的总质量,约束条件为金属骨架最大挠曲、二力杆的长细比、压杆稳定性与杆件的强度,优化数学模型为
(5)
式中:P1、P2、P3为上弦杆角钢截面的长、宽、厚;P5、P7、P9、P11为下弦杆、节点支撑杆、支座处斜腹杆、中间腹杆的外径;P6、P8、P10、P12为对应杆件的内径;P13为骨架整体最大挠曲;P14为二力杆中受压杆最大轴力;P15、P16为杆件所受的最大压应力与拉应力;优化目标是使得P21最小.
使用Optimal Space-Filling Design法生成样本点,删除杆件内径大于外径的样本点后共有151个样本点.计算每个样本点并使用响应面法对输入、输出参数进行拟合,得到了3个候选点,取3个点设计参数的均值并圆整后作为最优解,对所得的4个设计点进行计算验证,如图14所示.可见以最优解的验证点为基准,其余7个点的误差值均在10%以内,证明拟合度较高.

图14 拟合误差对比图
图15为各设计变量对输出变量的影响.从图15中可以看出:1)上弦杆、下弦杆和中间腹杆的截面尺寸对金属骨架刚度影响最大,且为正相关;2)上弦杆和支座处斜腹杆的截面尺寸对二力杆中受压杆所受轴力影响最大且呈现负相关趋势,而下弦杆以及节点支撑杆的截面尺寸与二力杆所受轴力呈现正相关;3)加长上弦杆角钢的截面长度能有效降低上弦杆所受压应力,加宽截面宽度则能有效降低其所受拉应力;4)对结构整体质量影响最大的是弦杆角钢的截面宽度和中间腹杆的内径.
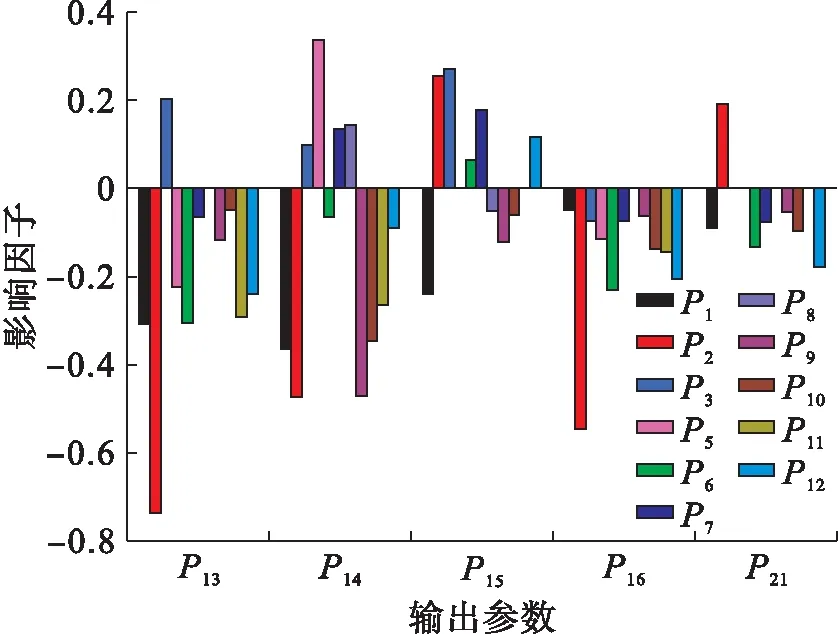
图15 设计变量对输出变量的影响
立面骨架膜结构的各杆件尺寸与总质量如表2所示.经优化后结构总质量为1 277.3 kg,降低了14.73%.

表2 骨架膜结构优化前后参数对比
6 结 论
本文通过分析得出以下结论:
1)基于ASNSY平台采用双向流固耦合方式对某项目中的骨架膜围护结构进行不同风向角下的定常风场仿真,得到了结构在不同风向角下的表面风压分布.
2)将所得风压数据与TTU实尺模型场地实测数据、同济大学风洞试验数据和建筑结构载荷规范进行比照,验证了数据的合理性与准确性.
3)采用双向流固耦合方式将所得风压耦合到骨架膜结构上,分析不同风向角下该建筑骨架膜结构各组成部件所受荷载情况,以此为据,将主要受力杆件与受力较小杆件的截面尺寸分开进行设计优化.
4)基于ANSYS的优化设计模块,以不同风向角下的骨架膜结构表面风压分布为基础,选取对结构最不利的极限荷载工况组合作为施加荷载,将金属骨架整体最大挠曲、二力杆的长细比、压杆稳定性与杆件的强度作为约束条件,以最小化结构总质量为优化目标,对各类杆件的截面尺寸进行优化.
5)本文基于流固耦合技术与响应面优化法,得到了该骨架膜结构中各杆件的截面尺寸对结构受力的影响关系,并将该结构质量降低了14.73%.
