基于超声波断层图像的三维重构方法

马世博，刘宏伟，迟永波，王奕博，张 昭

(1.河北科技大学 a.材料科学与工程学院，b.河北省材料近净成形重点实验室，石家庄 050018；2.上海新孚美变速箱技术服务有限公司，上海 201100；3.河北京津冀再制造产业技术研究有限公司，河北 沧州 062455)

工业CT(computed tomography)技术又称工业计算机断层扫描成像技术，是一种重要的无损检测技术，可以实现零件的断层扫描及模型重构，具有检测直观、数据精确和零件无损等特点[1].工业CT依靠放射性核素为发射源，因而会产生辐射，需在铅制隔离房内检测，进而限制了使用环境，且软、硬件成本较高[2-3].

随着超声波技术的不断发展，在20世纪初出现了超声波CT技术，受到众多学者的广泛关注，多位学者对超声波CT技术及应用开展了相关研究.张蕾等[4-5]研究了小波包变换在超声波CT特征提取中的应用，实现了超声波CT的特征提取，分析总结了超声波CT技术的多种发展与应用方向.刘帅鹏[6]使用超声波CT技术对桥梁灌注桩进行检测，得到桩座的三维CT成像图.邹云等[7]通过激光超声检测方法测定了板材弹性模量.Mohd-Khairi等[8]将超声波CT技术应用于盒装牛奶内部异物检测，构建了断层图像重建算法.Abbaszadeh等[9]设计了钢管输送机的超声波CT扫描系统，实现了管道超声波CT断层图片获取.目前已经实现利用超声波CT技术对典型零件断层图像进行获取，但超声波CT图像的特征分辨对检测人员要求较高，需要具备一定理论知识和检测经验.将超声波CT图像转化为三维模型可以直观表达零件形貌与内部损伤情况.目前超声波CT图像三维重构技术研究人员较少，研究方向存在空缺.基于超声波CT断层图像三维重构技术研究可以克服传统CT技术的不足，降低零件可视化技术成本，拓展无损检测人机交互渠道，对无损检测技术与智能工业体系的发展具有一定意义和价值.

本文拟对超声波CT技术检测的人工预制缺陷零件断层图像进行模型重构.通过噪音去除、异常信号调整、信号增强等方法对二维图像进行处理，建立轮廓提取算法处理图像并优化，得到可用于模型重构的断层图像.建立图像堆叠算法及模型重构算法，对预制损伤零件的断层图像进行模型重构.

1 模型重构方法

超声波CT模型重构流程如图1所示.通过超声波CT图像采集、二维图像处理、三维模型建立实现零件模型重构.利用相共阵检测方法进行超声波CT图像采集；基于Matlab软件构建图像二维处理算法，从灰度转换、噪音处理、轮廓提取三个方面对图像进行处理；利用Matlab软件构建重构算法来重构损伤模型.

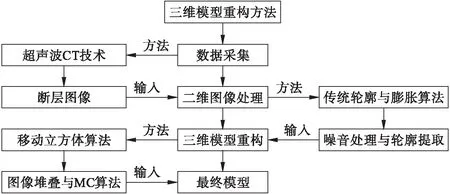
图1 模型重构流程图

1.1 图像采集原理

CT成像的实质是对扫描得到的每个点的投影数据进行计算得到各点的衰减系数，奥地利科学家拉东(Radon)提出的拉东变换与反变换实现了历史上的首次CT图像重建[10].这种方法同样适用于超声波CT成像，在性质相同的材料中声速变化不大，可以忽略超声波的衍射和折射.基于拉东变换分析投影数据，对被测介质参数(声速、衰减系数等)与接收数据之间的线性关系进行运算分析[11].选择二维线性超声波作为发射源，通过拉东反变换对CT图像进行重建，如利用FBP(filtered back projection)算法、代数重建算法等重建被测介质声学参量(声速、衰减系数等)的分布图像[12].

图2为超声波CT成像系统，通过计算机发射指令控制超声波发射器及支架的移动，再采集发射器信号与接收器信号并转入计算机进行处理，得到零件超声波CT断层图像.

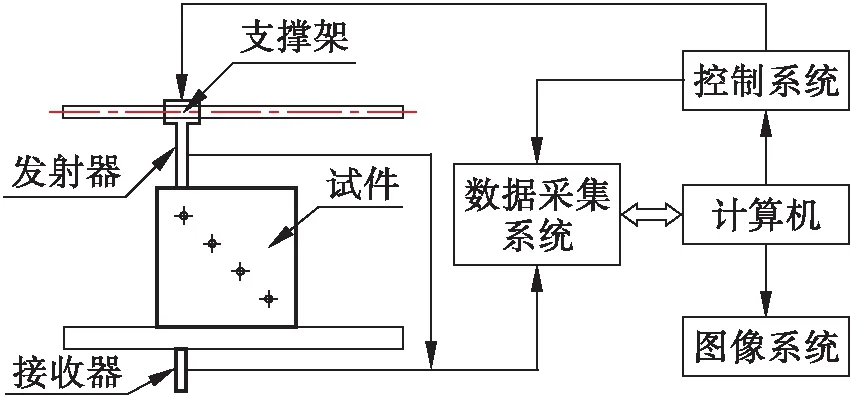
图2 超声波CT成像系统

1.2 二维图像处理方法

由于超声波成像具有对比度差、噪声污染高的固有特性，其图像中组织特征模糊，噪声干扰已成为影响超声图像质量的关键因素之一[13].因此，基于Matlab软件构建自适应滤波算法对图像进行降噪处理，并将图像转换为灰度图像后提取出轮廓边界.利用边缘检测算法对图像信号轮廓进行提取.目前常见的边缘算子较多，主要有Robert、Sobel、Prewitt、LoG、Canny算子等，各种算子特点[14]如表1所示.

表1 算子特点比较

由于超声波CT检测得到的图像边界并不明确，特征位置灰度值存在梯度渐变且存在一定的低噪音.综合考虑表1中各种算子的优缺点，采用适用于低噪音与灰度渐变的Prewitt算子对图像边缘进行提取.Prewitt算子原理是对图像进行阈值控制，将灰度值达到阈值的点均认为是边缘点[15]，即选取合适阈值K，若点G(i，j)≥K，则G(i，j)为边缘图像点.

通过计算像素点上下左右临点的灰度值插值判断边缘位置.在图像空间上利用两个不同方向模板(分别检测水平边缘与垂直边缘)对图像进行邻域卷积，其算子卷积核可以表达为

(1)

(2)

针对图像中的像素点G(i，j)，Prewitt算子可以定义为

G(i)=|[f(i-1，j-1)+f(i-1，j)+f(i-1，j+1)]-[f(i+1，j-1)+f(i+1，j)+f(i+1，j+1)]|

(3)

G(j)=|[f(i-1，j+1)+f(i，j+1)+f(i+1，j+1)]-[f(i-1，j-1)+f(i，j-1)+f(i+1，j-1)]|

(4)

可见，Prewitt算子实际上是先进行非归一化的均值平滑，然后再进行差分，这样在进行轮廓提取的同时也可以去除一定的噪音影响，实现对二维图像轮廓的提取.

1.3 三维模型重构方法

二维切片图像的每张图像均为独立数据，要实现模型重构首先需将二维数据进行连通构成三维数据组.因此，建立图像堆叠算法对处理后的二维数据进行排序并导入Matlab工作区，然后对数据进行维度扩张并确定图像的Z轴位置，进而实现图像的三维堆叠[16].

移动立方体算法的基本原理是在两张图像像素点的某个区域内进行采样，若采样点在x、y、z三个方向上的分布是均匀的，采样间距分别为Δx、Δy、Δz，则数据可以用三维矩阵来表示[17].图3为三维体素模型.

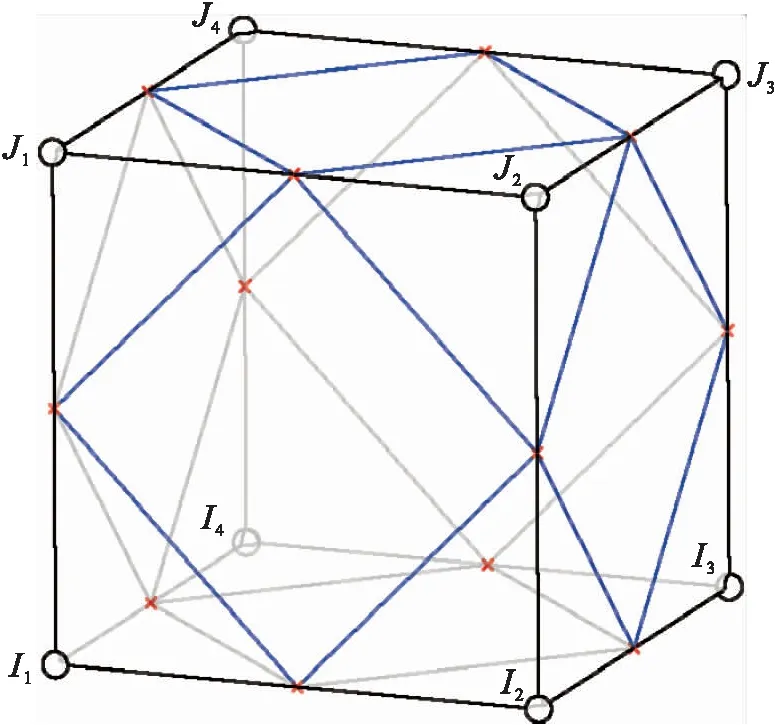
图3 三维体素模型

每8个相邻采样点(体素的角点)构成一个立方体成为一个体素，由于采样点是离散的，可以利用三线性插值法通过角点值计算体素内的任意一点的数值[18].将区间点数值作为依据建立面片顶点与平面法线.移动立方体算法构建流程为：

1)将断层图像读入内存；

2)扫描两张断层图像，分别利用两张图像的4个像素点创建一个立方体；

3)比较立方体顶点处的8个密度值与曲面常数并计算立方体的索引；

4)利用索引从预先计算的表格中查找边列表；

5)通过线性插值找到曲面边交点；

6)利用中心差计算每个立方体顶点的单位法线，对每个三角形顶点的法线进行插值处理；

7)输出三角形顶点和顶点法线.

2 超声波CT图像采集及处理

试验设备选用北极星辰挺杆C扫描成像系统，此系统具有较为完备的超声波扫描功能，可以实现超声波CT成像与3D层析扫查.

2.1 超声波CT图像采集

图4为零件模型与采集结果.预制损伤零件尺寸为50 mm×50 mm×125 mm，其中人工预制圆孔缺陷直径为1 mm、深度为5 mm，选择试件中均匀分布的4个圆孔作为检测对象，其位置分别为10 mm×10 mm、20 mm×20 mm、30 mm×30 mm、40 mm×40 mm处.图4b为不同位置的扫描断层图像，可以准确反映不同断层的损伤形貌.图4c、d为在顶部与正面C扫描图像损伤在模型中的具体位置.

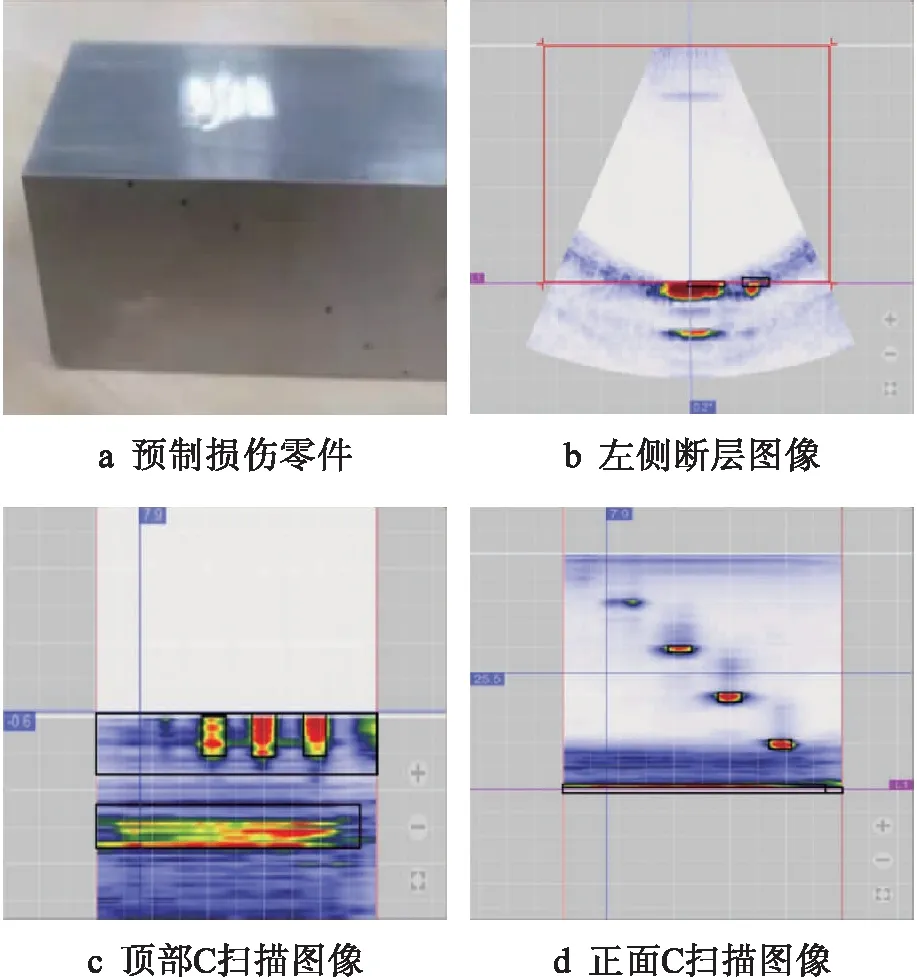
图4 零件模型与采集结果

2.2 二维图像处理及算法优化

对采集到的超声波CT图像进行预处理，先将图像转变为灰度图像并使用自适应中值滤波方法对图像进行降噪处理.去除图像中由于外界噪音所引起的异常信号，借助Matlab软件编写自适应中值滤波算法.自适应中值滤波器的基本原理[19]是比较一定领域内像素值的大小，取出其中值作为该领域中心像素的新值，同时根据预设好的条件，动态改变中值滤波器的窗口尺寸，以同时兼顾去噪声作用和保护细节效果，相应算法伪代码可以表示为

算法1：输入Sxy，Smax；

窗口像素值按大小排列；

计算Zmin，Zmax，Zmed，Zxy；

计算A1=Zmed-Zmin，A2=Zmed-Zmax，

B1=Zxy-Zmin，B2=Zxy-Zmax；

ifA1>0且A2<0

ifB1>0且B2<0

printfZxy

else

printfZxy-Zmed

else

增大Sxy

ifSxy>Smax

printfZxy

else

重复算法

其中：Zmin=min(Sxy)为窗口Sxy中的最小灰度值；Zmax=max(Sxy)为窗口Sxy中的最大灰度值；Zmed=med(Sxy)为窗口Sxy中的灰度中值；Zxy为坐标(x，y)处的灰度值；Smax为Sxy允许的最大尺寸.

图像降噪处理效果如图5所示.完成图像噪声去除后，利用Prewitt算子进行轮廓提取.根据超声波信号特性可知，图像转为灰度图像后缺陷位置灰度值不均匀，利用Prewitt算子运算得到的图像边缘存在丢失，计算结果中存在杂点且不连贯，图像断裂较多，不能达到预期结果.因此，再利用腐蚀膨胀开运算方法对轮廓进行进一步处理.

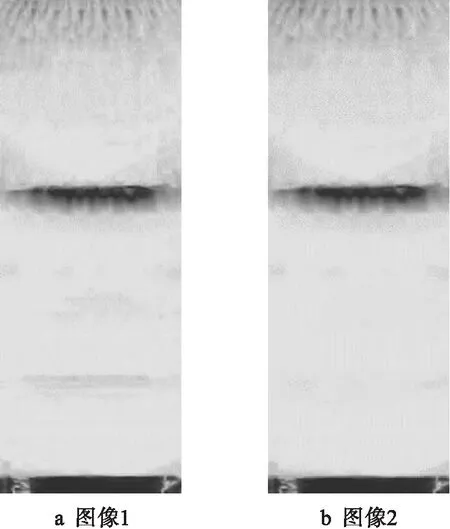
图5 图像降噪效果

膨胀算法与腐蚀算法原理[20]相似，通俗来讲腐蚀即是删除对象边界某些像素；而膨胀则是为图像中的对象边界添加像素.对腐蚀与膨胀图像进行交集运算就可以得到轮廓信息.腐蚀膨胀开运算方法是先腐蚀后膨胀的运算方法，可以实现图像中的小像素去除，从而达到一定去噪效果.利用膨胀后的图像与腐蚀图像相减即可得到膨胀腐蚀处理后的边界轮廓模型.轮廓提取算法逻辑可以表示为

算法2：读取图像；

定义图像灰度值范围；

设置灰度阈值T；

定义梯度算子卷积模板Prewittx，y；

对图像像素点G(i，j)进行运算；

ifG(i，j)≥T

(i，j)为边缘点

else

(i，j)为非边缘点

输出边缘点图像；%Prewitt算子运算结束

设置灰度阈值P；

根据P将灰度图像转为二值图像；

设置膨胀腐蚀结构元素SE；

腐蚀运算I；

膨胀运算J；

膨胀与腐蚀图像求差K=J-I；

输出处理图像；%图像开运算

利用Matlab软件编写Prewitt算子算法的处理结果如图6a所示，通过图像开运算方法优化轮廓算法处理后的轮廓图像如图6b所示.可见，通过优化算法处理的图像无杂点、断点等现象，图像轮廓连续边界清晰，可以用于三维模型重构处理.

图6 轮廓提取结果

2.3 模型重构

对处理后的二维图像进行数据对齐与堆叠，添加z轴方向数据对图像进行排列，将二维数据转化为三维数据并实现二维图像之间的数据信息链接，其基本原理是对图像进行编号与读取，采用图像名作为标记，以此标记作为图层信息并通过循环语句将多个数据堆叠在一起，具体数据堆叠算法可以表示为

算法3：读取图片位置与格式；

标记文件名样式；

length(names)=文件标号最大值；

a=文件名编号；

IMAGES=定义一个全为零的空矩阵；

fork=1：length(names)

nm=[当前编号的文件信息]

image=写入(nm)

IMAGES(：；：；k)=image

end

保存IMAGES.mat；

随后对堆叠数据进行体素分割，计算出各个体素中的像素点值，将各顶点与法线的相对位置连接为等值面，所有体素中等值面与法线信息构成整个数据的三维模型.利用Matlab软件构建的模型重构算法可以表示为

算法4：读取数据文件(IMAGES.mat)；

for(对每一个物体)

{

扫描两层链表结构INCIDENCE；

for(对每一个体素单元)

{

查表找到三角面片分布情况；

根据平面方向和所处位置将三角面片加入INCIDENCE

}

初始化三角面片链表FaceList、顶点链表PointList和多边形链表PolyList；

for(对INCIDENCE中的每一个平面)

{

清空用于合并的二维数组Merger；

for(对于该平面上的每个三角形或矩形)

{

查表找到三角形或矩形的边对应于Merger中的编号，写入Merger；

}

扫描Merger，将图形划分为凸多边形，加入PolyList；

}

将PolyList中涉及到的顶点加入PointList，同时建立顶点的逆向索引；

for(PolyList中的每个凸多边形)

{

检查其边界上(不含端点)是否有点存在；

找到“T”型点，加入该多边形，同时进行标记；

进行三角划分并将三角面片加入FaceList；

}

清除PolyList；

清除INCIDENCE；

将FaceList中的数据转移到数组Face-Array中；

清除FaceList；

将PointList中的数据转移到数组VertexArray中，同时进行插值；

清除PointList；

}

对所有顶点计算其法矢量；

输出三维模型；

图7a为采用算法3进行数据堆叠的结果，经过数据堆叠后，二维图像间的通道已经建立，可以借助侧视图堆叠数据观察到正视方向上的图像特征.图7b为采用算法4处理后的模型重构结果，模型外部轮廓与内部损伤情况清晰可见.

图7 三维重构模型

2.4 模型数据对比

借助建模软件进行数据测量，利用二维视图工具截取模型的中间断面部位，结果如图8所示(单位：mm).由图8可见，断面图中的缺陷形貌、外形特征及缺陷位置与实际相符，模型外形尺寸与损伤部位的形位偏差均在1 mm之内，即模型外部轮廓与损伤位置还原精度较高，但重构模型在损伤形貌还原方面还不够精确.

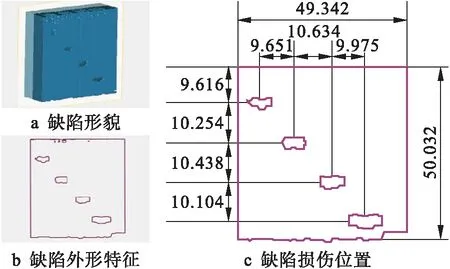
图8 重构模型断面图

由分析结果可知，超声波CT技术检测断层图像方法检测成本较低、安全性高、检测迅速，可以作为一种传统CT图像的替代方法实现模型重构.虽然重构技术仍存在一定不足，但超声波CT断层图像为模型重构技术带来新的发展方向和更大的应用空间，对模型重构算法的开发与研究具有一定的学术价值与广阔的应用前景.

3 结 论

通过以上分析可以得到如下结论：

1)通过Matlab软件构建轮廓提取与三维重构等算法，实现了超声波CT断层图像的模型重构，验证了本文提出的模型重构方法的可行性.

2)Prewitt和Robert算子轮廓提取算法对超声波CT图像处理效果不理想，综合分析后利用膨胀腐蚀算法对Prewitt算子进行优化，改进后的轮廓提取算法可得到清晰完整的轮廓信息，从而实现超声波CT图像的特征信息提取.

3)利用构建的模型重构算法对超声波CT图像进行模型重构的结果显示，零件外部和内部形貌完整且尺寸准确，外形尺寸与损伤位置偏差约为1 mm，但零件的损伤形貌重构不够精细，有待改进与优化.