航线联营下基于转运的飞机航线路径优化
2023-02-09闫妍马啸来
闫妍,马啸来
(1. 西安财经大学 管理学院,西安 710100; 2. 西南交通大学 交通运输与物流学院,成都610031;3. 西南交通大学 综合交通运输智能化国家地方联合工程实验室,成都610031)
中国航空运输货运量逐年增加,航空基础设施建设加快,枢纽机场的作用日益显现,整体上我国航空物流发展速度很快,但仍存在如航空货运的资源闲置导致的高成本等问题。因此,本文以降低航空运输企业的运营总成本为目标,对飞机航线路径进行优化研究。
目前国内外对研究航空联盟环境下飞机航线路径优化的研究较少,对航线网络优化的研究集中在线路优化[1-2]、航线调配[3-4]、飞机排班优化[5]方面。多采用定性与定量分析方法优化航线,通过建立的指标评估体系、数学模型,采用决策树法[6]、聚类法、迭代法[7]、松弛法[8]等精确算法,设计遗传算法[9]、列生成算法等启发式算法,也有部分采用数学求解器,如MATLAB 优化工具箱[1]、CPLEX[10]等软件解决模型,确定最优航线。联盟环境下的飞机航线路径优化研究主要有王苗苗[11]基于航空节点联盟,不考虑枢纽点的建设成本,以网络总成本最小化为目标,构建航线网络优化模型,并求解分析航空网络布局。不考虑航空联盟的飞机航线路径优化研究中的选址-路径问题(location-routing problems, LRP),杨忠振等[12]构建总运输成本最小化的双层规划模型,确定航空枢纽点选址及航段上的指派路径。不考虑航空联盟的飞机航线路径优化(fleet route optimization,FRP),裴一麟[5]构建航线网络航班时刻双层优化模型,利用二分法精确求解航班时刻、各航线的成本和总成本。Armacost 等[13]同时确定联合包裹服务(united parcel service,UPS)飞机航线、机队分配和包裹路线,确保以最低成本实现隔夜交付,并应用复合变量法解决模型。
基于现有研究,本文将研究点点式、轴辐式组成的混合式航空货运网络的转运点选址与飞机航线路径优化问题。本文的创新性在于引入航空联盟运营选择概率函数,构建联盟环境多起讫点的航空货物中转及飞机航线路径优化模型,并设计自适应遗传算法求解模型。
因此,本文将以航空联盟为基础,解决航空货运中转点选址及飞机航线路径优化问题,以转运点数量及转运次数为限制条件,不考虑飞行过程中的时间成本及等待时间成本,以总成本最小化为目标,建立了航线联营下基于转运的航线路径优化模型(aircraft fleet route problem based on transshipment and airline alliance, T-AAAFRP)。采用改进的遗传算法求解模型,并通过案例分析航空线路联盟下的航空中转点选址、飞机飞行路径及在不同转运点限制条件下的选址及路径问题。
1 问题描述
本文研究的问题可描述为在已知货运需求起终点i、j的位置及需求量Dij的基础上,考虑航空网络中单、双机场城市飞机容量限制,实际运行中全货机飞行时段及空域容量的限制,联盟其他航司的飞行时段及空域容量的限制。任意一架飞机必须从航空基地集合O∈[1,2,...,N]出发,完成一天运输任务后,返回到出发航空基地。并考虑联盟对运营的影响,引入航空联盟选择概率,确定非转运、转运前后各航段运输的承运及托运问题,若存在运输无法完成的情况,则需要承担相应的惩罚成本。因此,本文是研究航线联营下基于转运的航线路径优化问题,即T-AAAFRP 问题。航线联营下基于转运的飞机航线路径优化问题示意图如图1 所示。

图1 基于转运的飞机航线路径优化问题示意图Fig. 1 Aircraft route optimization based on transshipment
2 模型假设及建立
2.1 模型假设
飞机飞行过程中的运量反应示意图如图2 所示。T-AAAFRP 问题建模思路如图3 所示。

图2 飞机飞行过程中的运量反应示意图Fig. 2 Traffic response of aircraft in flight

图3 T-AAAFRP 问题建模思路Fig. 3 Modeling ideas of T-AAAFRP problem
1) 货物转运最多1 次。根据大多数航空货运转运的研究,转运次数限制在1~2 次最好,本文根据文献[14]中的转运最优结果,因此假设转运最多1 次。
2) 不考虑飞机降落的排队问题。假设飞机降落所需时间一样,且错开时间降落,因此不存在排队问题。
3) 转运货物计算2 次装卸费用。根据物流转运业务费用核算的一般规律,对转运货物计算2 次装卸费用。
4) 转运过程中不考虑时间等待成本。若飞机在枢纽点不等待,直接飞往下一航段,只需将转运的货物在枢纽点卸下,并等待下一飞机到达枢纽点后飞往目的地,其中货物的时间等待成本不计,但是枢纽点暂存货物,需要支付枢纽点固定成本;若飞机在枢纽点等待,则还需要承担停机费用。
5) 运输过程中各航段的单位运输成本相同。飞机的单位运输成本与飞机的类型相关,假设所用的飞机类型一致。
6) 航空公司所有的需求点及转运点都是航空公司承运。
7) 航线承运时,任意2 个航空节点间的货物只能沿着一条运输成本最小的航线完成运输。航空公司在运营中,以成本最小为目标,则必选择成本最小的航线完成运输。
8) 枢纽点的容量限制与机场数相关。假设双机场城市选择枢纽点的容量限制是单机场城市选择枢纽点的容量限制的2 倍。
9) 若航段运营托运时,则该航段航空公司的承运货运量为0。
2.2 航空联盟运营选择概率函数
当航空公司选择加入联盟时,不同航段上的运营选择与其货运量、其他合作航空公司货运量及其他合作航空公司运营选择有关。
当航空公司选择联盟承运时,效益为

采用改进的风险价值函数,评估风险损失大小,风险价值函数为

2.3 基于转运的飞机航线路径优化模型
对于转运中心选址,一般采用枢纽选址模型[15],解决需求点间的枢纽转运问题。针对飞机航线路径优化,一般采用FRP 模型[16],解决飞机路线设计、航空运输问题。因此,本文将以总成本最小化为目标函数,建立基于转运的飞机航线路径优化模型:

式 中:yij为 航 段i到j选 择 承 运,服 从0~1 分 布;CTik j为 点i经 点k到点j的单位运输成本,CTik j=θ1CTik+θ3CTk j≈θ(CTik+CTk j),总 运 输 成 本 与 重量、距离相关, θ1、θ3为直达成本与转运成本之间系数,且与运输航段有关, θ为标准的直达成本与转运成本之间系数,可简化表示为 CTik j=θ(CTik+CTk j),dik j为 点i经 点k到 点j的 距 离,dik j=dik+dk j;POk j为 转运前的出发点是基地的概率。
装卸降落成本,包括航段直达与转运两部分:

无人运输的惩罚成本:


3 算法设计
3.1 算法选择及流程
本文研究的航空公司转运点选址和飞机路径联合优化问题,需要解决的问题有:①确定货物的转运点;②每架飞机的飞行路线。
对该类联合优化问题的求解大多采用遗传算法,考虑本文研究属于LRP,也将采用遗传算法求解,本文研究的创新性是基于有向需求的优化问题,因此,将基因工程中的剪切技术运用在遗传算法的交叉与变异过程中,设计自适应遗传算法求解转运点选址及飞机路径优化问题,优化过程如图4 所示,其中,终止条件1 为:需要将所有的需求点全部计算完,终止条件2 为:根据计算结果,与上一轮的结果比较留质最优的结果,且迭代次数达到了规定。

图4 算法流程Fig. 4 Algorithm flow
3.2 算法改进及设计
步骤 1 改进编码形式及参数初始化,改进的编码形式如图5 所示。

图5 改进的编码形式Fig. 5 Improved coding form
采用分段编码的形式,分为2 段。第1 段采用整数染色体编码形式,共有K个个体,表示K个中转点,每一个染色体基因代表第几个机场被选为中转点。第2 段采用向量编码的形式,在可行域内随机产生M×M个个体,且将第2 段编码分为3 个部分,第1 部分代表基地机场出发的需求,第2 部分为需求点的需求,第3 部分代表返回基地机场的需求,构成初始种群。若有2 个航空基地,10 个需求点,则将产生一条10×10 的群体,编号为[(1,3),(3,4),(4,5),(5,1),(1,2),(2,6), (6,7),(7,8),(8,2),(2,1),(1,9),(9,10),(10,1)],代表相应的路径,需要3 架飞机进行运输,路线1 为1-2-3-5-1,路线2 为2-6-7-8-2,路线3 为1-9-10-1。
步骤 2 基于备选点确定转运中心初始解。在给定的K1个 备选点中,随机选择确定K个个体,作为转运点初始解。
步骤 3 染色体解码。染色体解码的目的是为了获取每一架飞机所运输的起终点需求,即OD 对解码的具体过程如下:①初始化一条路径;②将染色体中的基因值顺序插入到当前路径中,其中经中转运输的航段必须符合转运点的约束条件,若1 个基因值的插入导致该路径的负荷超过了飞机、航段的最大容量或飞机飞行时长的约束,则开始构建新的路径;③重复1、2 操作,通过扫描方式直至所有OD 对均被插入到路径中分割成多个染色体,最终形成一个可行解。若有2 个航空基地,10 个需求点,则将产生1 个可行解。为避免出现不可行解等问题,在该步骤按照假设条件及约束条件,进行解码,确保解的可行性。假设染色体的编码为[(1,3),(3,4),(4,5),(5,1),(1,2),(2,6),(6,7),(7,8),(8,2)],初始化一条路径(即一个空的数组),将染色体的基因依次插入路径中,假设当插入“(1,2)”时,该路径的负荷超过了飞机的最大容量或飞机到达航段(1,2)时的时长超过了规定时间,则将1-2-3-5-1 分配给飞机1。因为染色体的基因还没有完全分配完,所以构建一个新的路径,将未分配的基因依次插入路径,假设插入到(8,2)时,该路径的负荷满足要求同时飞机飞行时长也符合规定,由于需求OD 对已经全部分配完毕,因此将2-6-7-8-2 分配给飞机2。至此解码结束。
步骤 4 生成禁忌表。根据各需求OD 对,可随机生成一条染色体,应用式(23)计算转运选择,如图6 所示。

图6 初始禁忌表示意Fig. 6 Diagram of initial taboo list
步骤 5 生成路径初始解:①根据航段上总的OD 需求,应用航司随机选择均衡函数,初步确定不同航段上的运输选择行为;②总OD 需求合并后若大于1 架飞机总载重时,多余的航段需求OD 全部托运,该位置记为空;③根据步骤3、4 的信息,依次连续选择飞机运输航线,且出发点为1,2 开头的航空基地,返回点也需为1,2 结尾,当1 架飞机新增1 个航段任务导致飞行时间超过24 h,则返回上一航段结束,并将已完成运输航段记为-1;④当2 架飞机完成1 个经转运的OD 需求时,若后一段运输发生时间早于前一段,则需要将后一段需求托运,将转运后联盟承运记为0,更新选择行为;⑤根据最新选择行为,将转运前后联盟承运记为1 的航段,按照第3 步重新生成路径,如图7 所示,[]表示自营飞机不承担运输,由联盟的其他公司承担运输。
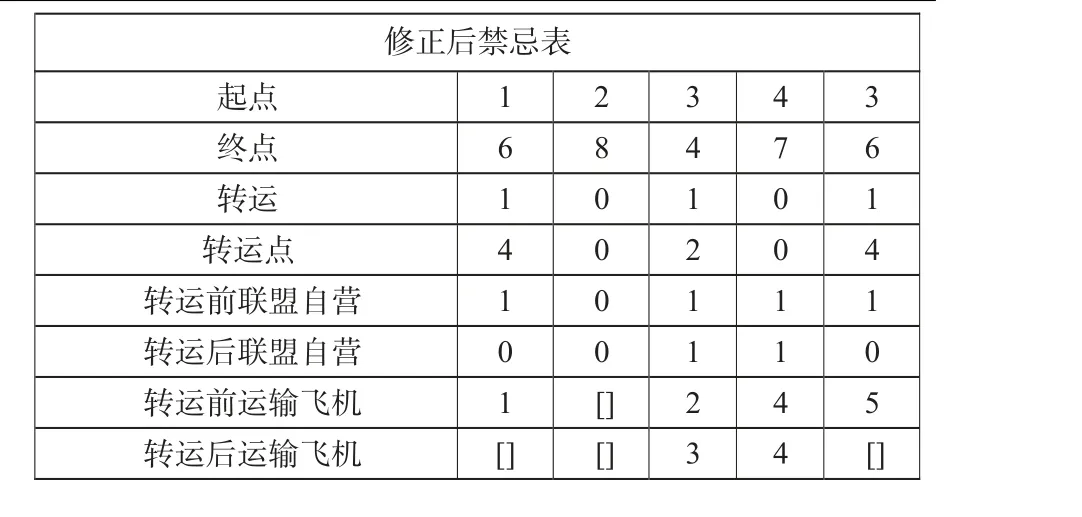
图7 修正后禁忌表示意Fig. 7 Diagram of revised taboo list
步骤 6 适应度值评价。根据式(10)~式(18),计算适应度值。
步骤 7 选择。根据步骤3、4、5 计算结果,采用锦标赛法进行选择操作,选择N/2染色体。具体选择方法为,当锦标赛法排序选择时,染色体z1锦标赛的大小大于染色体z2锦标赛的大小,染色体z2优 于染色体z1; 或当锦标赛值相等且染色体z2适应度值大于染色体z1, 染色体z2优 于染色体z1。
步骤 8 基于基因工程的交叉、变异。根据交叉概率pc,借鉴染色体重组技术,利用剪切酶思想,选择其中任意一段剪切,且将切割位点表示为剪切基因位,并在该条染色体的其他位置选择相同剪切基因位的任意长度进行剪切,并交换2 段的位置。此时2 段基因交叉可近似视为一般遗传算法的单点交叉,基于基因工程的染色体交叉过程如图8 所示。根据变异概率pm,和改进交叉方法相同,基于染色体中的某段基因,选择将其中一小段基因进行变异,同时在变异位置后,选择与前段基因连接相同的基因,并将该段基因中的一小段基因与前段基因变异,此时的2 段基因变异可近似视为一般遗传算法的单点变异,基于基因工程的染色体变异过程如图9 所示。

图8 基于基因工程的染色体交叉过程Fig. 8 Chromosome crossover process based on genetic engineering
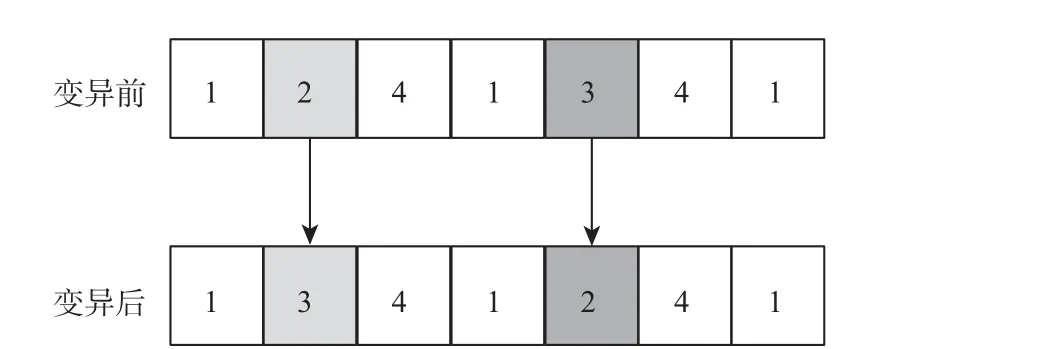
图9 基于基因工程的染色体变异过程Fig. 9 Chromosome mutation process based on genetic engineering
步骤 9 精英数目。合并父代及子代的种群染色体,形成新种群P(h),经过序值、拥挤度、交叉等操作得到下一代群体P(t+1),并按照适应度值升序排列选择染色体,最终选择H个染色体。
步骤 10 终止判断1。即需要将所有的需求点全部计算完后达到终止条件1,则终止程序,并通过结果验证,选择的染色体不能重复输出结果,否则返回步骤3。
步骤 11 终止判断2。即根据计算的结果,与上一轮的结果比较留取最优的结果,且迭代次数达到了规定,则终止程序,并通过结果验证,选择的染色体不能重复输出结果,否则返回步骤2。
4 算例分析
4.1 参数设置及基本情况
S 货运航空公司实际运营时,单位运输成本CT=0 .003 3 元/(kg·km),假设飞机的最大载重量Q=30 000 kg,每段航程所需的固定费用(包括飞机折旧)为CP=25 000 元/(架·次),装卸作业成本为CW=0.5 元/kg,飞 机 的 起 降 费 CPTL=20 000元/(架·次),无承运时的单位损失成本为CW= -0.001 元/(kg·km),航空基地分摊至每天的建设成本 CFo服从均匀分布U(300 000,400 000),每个基地的飞机容量限制QN服从均匀分布U[10 000,20 000],且双机场城市{上海、北京、成都}的容量限制Qi服从其他单机场容量限制的2 倍,即服从U[20 000,40 000]。枢纽点建设成本 CFk服从均匀分布U(20 000,40 000),枢纽转运运输成本系数为 θ=0.8,备选航空枢纽点数量为N=6,假设不同航段的容量限制服从均匀分布U[30 000,60 000],各航段的时间窗满足[U(0,18 000),U(0,18 000)+U(2 000,6 000)],超过飞行时间约束的惩罚成本e为500 000 元。已知航空公司基地为{4 深圳、5 杭州},航空枢纽点备选集合为{1 北京、2 广州、6 沈阳、7 郑州、8 武汉、9 成都},其他参数如表1所示。

表1 修正后禁忌表主要参数设置Table 1 Revised taboo list Main parameter setting
4.2 计算结果
改进的自适应遗传算法利用MATLAB R2016b软件,在Inter Core i7-8550U CPU @ 1.80 GHZ 1.99 GHz,8.00 GB 内存电脑上运行计算,通过数值实验分析改进算法的参数对计算结果的影响如图10 所示,求解算法的具体参数设置如下:种群大小 NP=100,交叉概率pc=0.8, 变异概率pm=0.8,最大迭代数G=100。当转运点数量为2 时,在第27 代算法收敛,说明设计的改进算法具有较高的收敛性,算法的迭代收敛曲线如图11 所示。

图10 种群大小对计算结果的影响Fig. 10 Effect of population size on calculation results
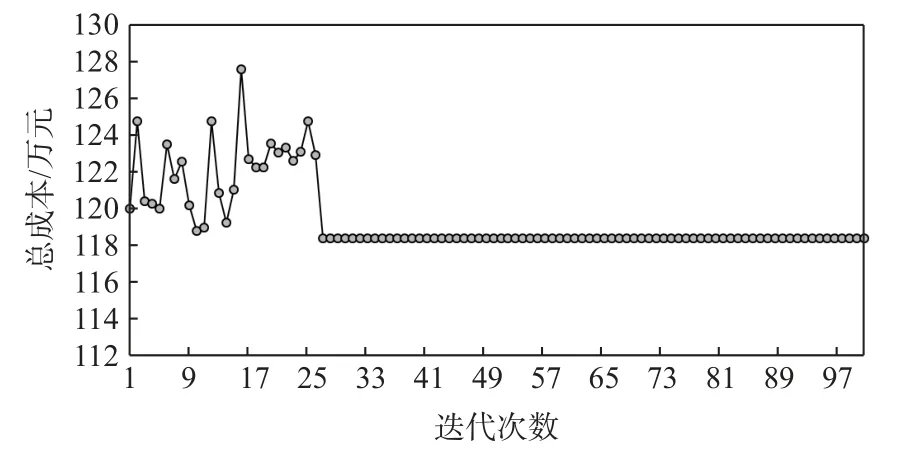
图11 收敛曲线Fig. 11 Convergence curve
不同转运点数量的优化选择结果如表2 所示,不同优化方案的最优飞机机队路线如表3 所示。从表2 可以看出,基地机场数量越多,总成本越小,且任意转运点数量时转运点都包含成都,即双机场所在城市,符合航空公司、机场各方业务发展需要。但是总成本越小的方案,不一定是最优的决策方案。企业的决策者需根据不同时期的需求确定不同的计划。当企业资本较小时,应选择表2 中的最优选择4 或5;当企业在市场扩充时,为赢得更多客户,应该选择表2 中的最优选择1 或2。

表2 不同转运点数量的优化选择结果Table 2 Optimal selection results of different number of transfer points

表3 5 种方案的最优飞机机队路线Table 3 Optimal aircraft fleet route of five schemes
4.3 敏感性分析
1) 不同需求量下的结果分析。不同转运点的数量及位置,在需求量倍数增长下,单位数量的总成本与飞机数量会有所增长,且增长率不断增大。总成本的平均增长率为-19.3%,飞机数量的平均增长率为106.8%。在同一种转运点类型下,单位数量的总成本与飞机数量的增长率相差不大,其中2 个转运点的总成本的平均增长率为-12.5%,飞机数量的平均增长率为41%;其中3 个转运点的总成本的平均增长率为-11.5%,飞机数量的平均增长率为60.1%;其中4 个转运点的总成本的平均增长率为-14.2%,飞机数量的平均增长率为91.7%;其中2 个转运点的总成本的平均增长率为-18.7%,飞机数量的平均增长率为111.6%;其中2 个转运点的总成本的平均增长率为-20.1%,飞机数量的平均增长率为122%。对比总体可知,当转运点数量越多,所节省的成本不断扩大,所使用的飞机数量也越多,如图12 所示。因此建议在企业运营决策中,多考虑多转运点的情况,降低成本。
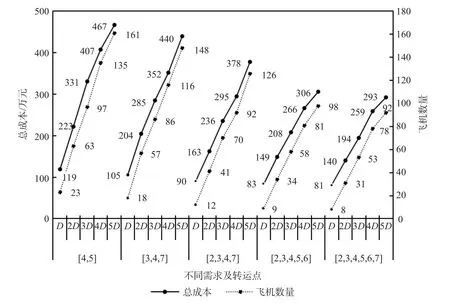
图12 不同需求量下的计算结果Fig. 12 Calculation results under different demands
2) 不同飞机载重量下的结果分析。不同转运点的数量及位置,在飞机载重量增长下,总成本与飞机数量有所下降,但趋势较缓。不同数量的转运点对比中,同一载重量的总成本随着转运点数量的增多而降低的幅度较大。随着载重量从30 000 kg,35 000 kg,40 000 kg,45 000 kg,50 000 kg 的变化过程,总成本平均增长率分别为-23%、-26.1%、-23%、-24.5%、-25%,飞机数量平均增长率分别为-45.7%、-48.9%、-50%、-53.3%、-54.5%,下降的趋势明显,如图13 所示。总之,转运点数量较少时,飞机的载重量对优化结果的影响较小,当飞机载重量较大时,决策者需考虑转运点数量多的方案。
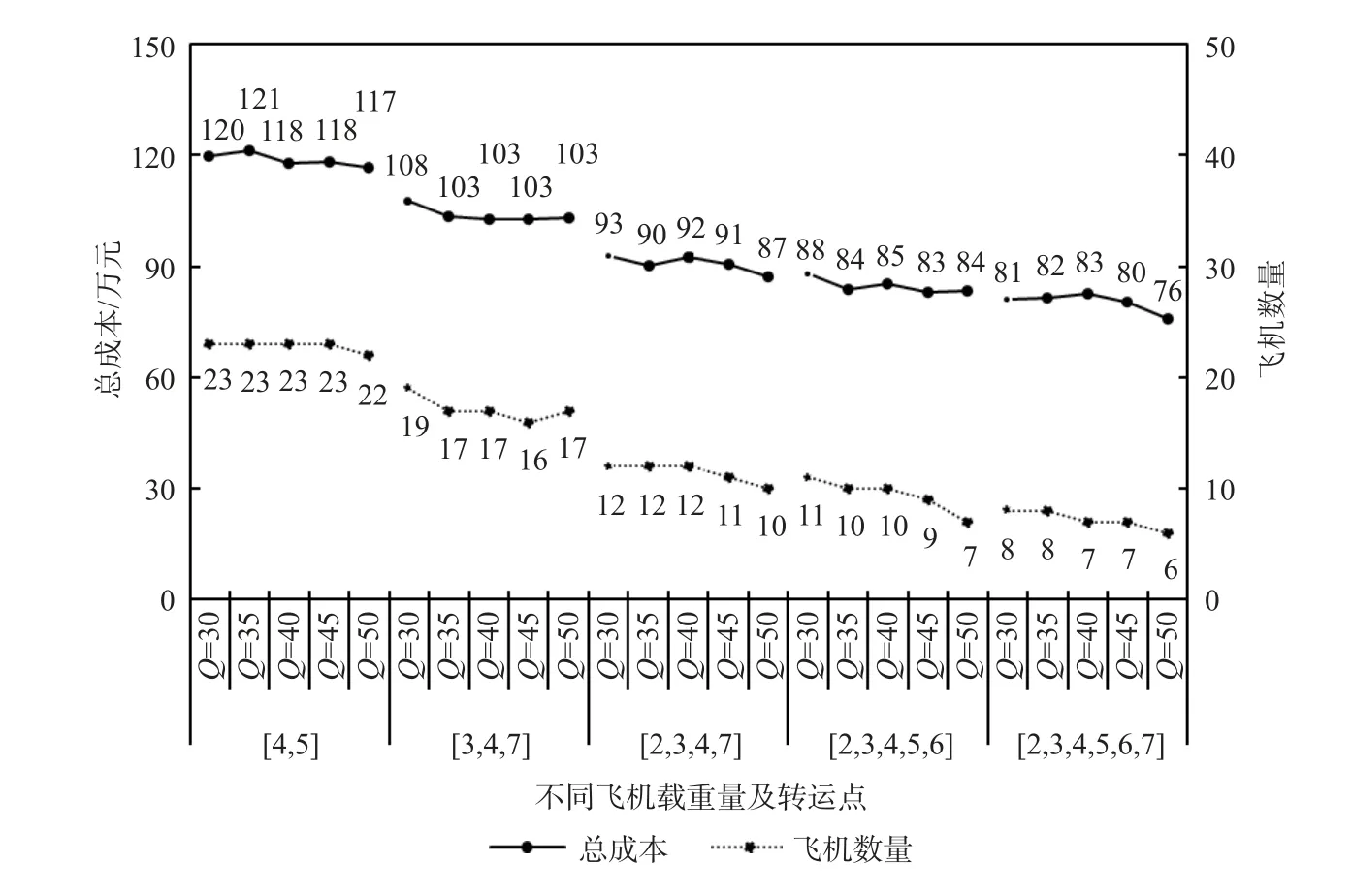
图13 不同飞机载重量下的计算结果Fig. 13 Calculation results under different aircraft load
3) 不同飞机固定成本下的结果分析。不同转运点的数量及位置,在飞机固定成本增长下,总成本与飞机数量会呈负增长趋势,且增长率逐渐趋于平缓。若飞机固定成本较小时,较多的转运点数量可以减少总成本、降低飞机使用数量。若当飞机固定成本较高时,转运点越多,则航空公司越多的无法进行承运运输,此时选择托运的概率越大。随着飞机固定成本从25 000 元,30 000 元,35 000 元,40 000 元,45 000 元的变化过程,总成本平均增长率分别为-24.5%、-23.7%、-10.3%、-7.2%、-9.7%,飞机数量平均增长率分别为-48.9%、-62.5%、-27.3%、-22.2%、-28.6%,下降的趋势明显,如图14 所示。总而言之,飞机的固定成本较少时,越多的转运点则总成本、飞机使用数量越小。当飞机的固定成本较大时,企业选择托运的概率越大。

图14 不同飞机固定成本下的计算结果Fig. 14 Calculation results under different aircraft fixed costs
4) 不同成本与收益的系数结果分析。不同的收益系数,较大程度影响决策。当收益系数保持不变时,转运点数量越多,总成本与飞机的数量越小,平均增长率分别为-25.5%和-48.6%。但当转运点数量保持不变时,收益系数越多,总成本与飞机的数量越多,平均增长率为56.3%和234%,如图15所示。因此,航空公司成本与收益的系数的大小对决策的影响很大,系数越大时,可选择转运点数量越少的决策方案。

图15 不同成本与收益的系数下的计算结果Fig. 15 Calculation results under different coefficients of cost and benefit
5) 不同航空联盟成本分摊系数结果分析。当航空联盟承运成本分摊系数 α一定时,随着托运成本分摊系数 β的增多,总成本平均增长率为5%,飞机数量平均增长率为17.3%。当航空联盟托运成本分摊系数 β一定时,随着承运成本分摊系数 α的增多,总成本平均增长率为-9.3%,飞机数量平均增长率为-22.4%,如图16 所示。总之,托运分摊系数越大,选择承运运输的概率越大,使用的飞机数越多,但同时总成本越大。反之承运分摊系数越大,航空托运的概率越大,使用的飞机数越少,但同时总成本越小。
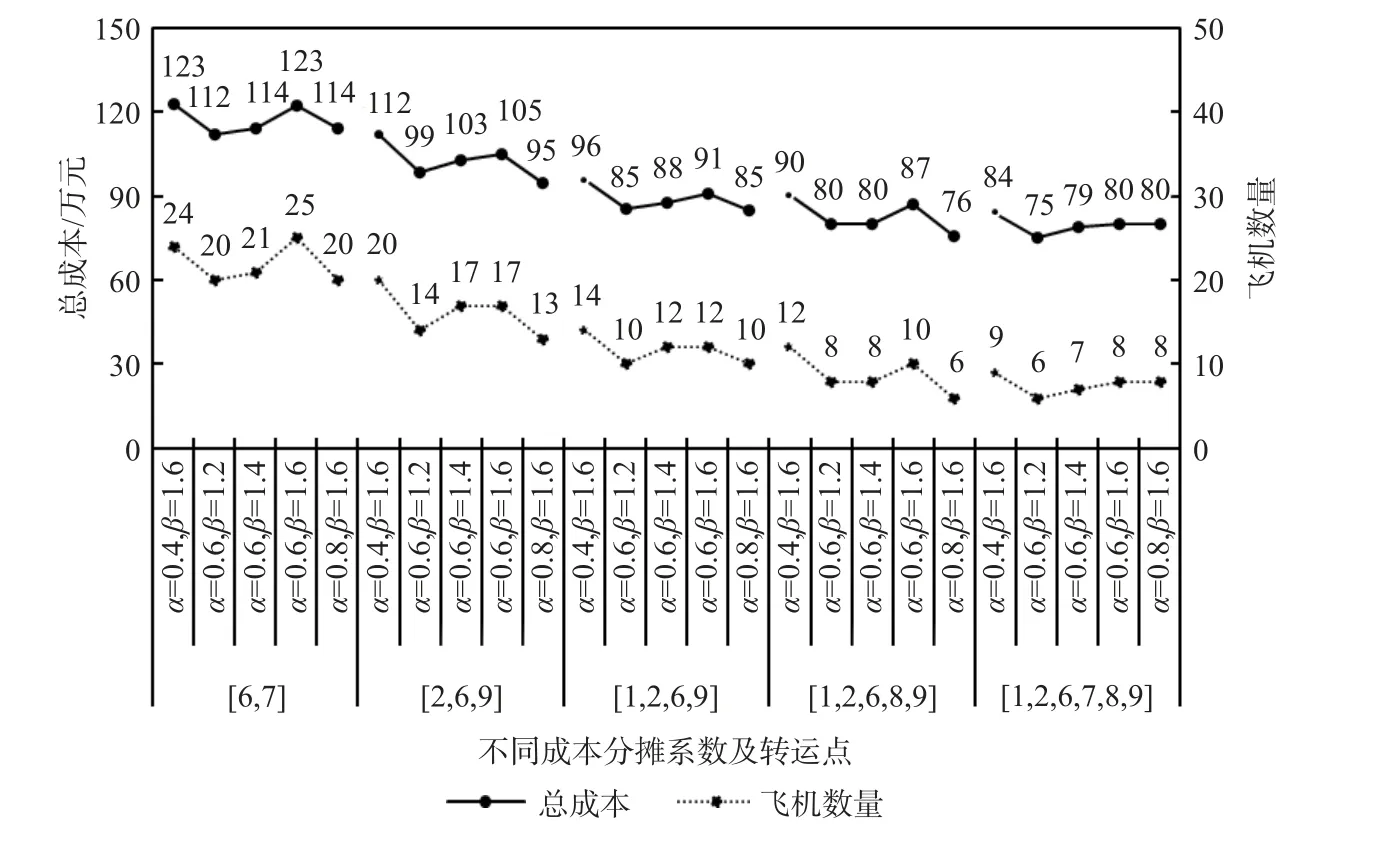
图16 不同航空联盟成本分摊系数下的计算结果Fig. 16 Calculation results under different cost sharing coefficients of aviation alliance
6) 决策者风险损失偏好不同参数的结果分析。①决策者对损失的敏感度。当转运点数量保持不变时,不同的决策者对损失的敏感度对优化结果的影响较小,总成本的平均增长率为3%,飞机数量的平均增长率为9.5%。但当决策者对损失的敏感度保持一定时,随着转运点数量的增多,总成本的平均增长率为24.4%,飞机数量的平均增长率为51.3%,如图17 所示。因此,决策者对风险损失敏感度越高,则选择承运的概率越大,此时所需的总成本、飞机数量越多。②风险损失时权重的大小。当转运点数量保持不变时,不同的决策者对风险损失时权重大小对优化结果的影响较小,总成本的平均增长率为0.4%,飞机数量的平均增长率为2.1%。但当决策者对风险损失时权重大小保持一定时,随着转运点数量的增多,总成本的平均增长率为25.6%,飞机数量的平均增长率为50.8%,如图18 所示。因此,决策者对风险损失时权重大小,对企业决策影响较小。若为取得更低的成本,应多采取转运点数量多的方案。
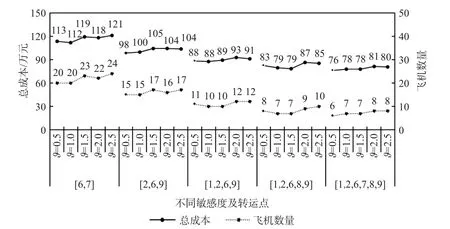
图17 不同决策者对损失的敏感度下的计算结果Fig. 17 Calculation results under different sensitivity of decision maker to loss

图18 不同风险损失时权重的大小下的计算结果Fig. 18 Calculation results under the weight of different risk losses
5 结 论
本文主要解决航线联营下基于转运的飞机航线路径优化问题。引入损失价值的前景理论,确定航空联盟选择概率函数,建立基于转运的飞机航线路径优化模型,将基因工程引入到交叉变异过程中,设计改进的遗传算法求解模型,最后通过案例分析,可得到以下结论:
1) 在转运点的确定过程中,当转运点数量超过3 个时,双机场城市被货运航空公司选为转运点的概率为1。当转运点数量较少时,转运点的位置一般集中在与基地位置较远的区域中心城市。在航空运输过程中,企业的决策与机场的建设之间相互影响。
2) 当货运航空公司航段上的货运需求量大于1/6 飞机载重量时,公司93.4%会选择直达运输,此时公司会选择自己承运航段上的业务。若当货运需求量小于1/80 飞机载重量时,公司90%会选择中转运输,但有56%会选择自己承运航段上的业务。
3) 需求量、飞机固定成本、收益系数的大小、承运成本与托运成本的大小对飞机航线路径优化决策的影响较大。飞机载重量的大小对飞机航线路径优化决策的影响较小,代表机型对优化结果的影响较小,在轴辐式网络及航线联营下,货运航空公司可自主选择任意飞机机型。
