使用三天线的联合定姿和欺骗检测方法
2023-02-09陈佳佳袁洪徐颖于丰正
陈佳佳,袁洪,徐颖,于丰正
(1. 中国科学院 空天信息创新研究院,北京 100094; 2. 中国科学院大学 电子电气与通信工程学院,北京 100049)
多天线的全球卫星导航系统(global navigation satellite system,GNSS)欺骗检测方法利用欺骗信号与真实信号之间的几何空间差异来进行欺骗检测,是当前GNSS 反欺骗领域的研究热点[1-3]。由于GNSS 卫星的几何空间信息几乎不可能被模仿,因此,多天线的欺骗检测方法已经成为最有效的欺骗检测方法之一[4-5]。使用多天线的欺骗检测方法通常基于2 种思路。第1 种思路基于所有欺骗信号来自同一方向的假设[6-7]。当不存在欺骗源时,由于真实信号到达方向各不相同,不同卫星的载波相位值也应存在明显的差异。当存在欺骗源时,欺骗源的天线会播发多路欺骗信号,欺骗信号的到达方向完全一致,对应的载波相位差值也基本相同[8]。该方法可以有效地检测出单个天线广播多个欺骗信号的情形。但当存在来自多个方向的欺骗信号时,该方法可能会失效。
第2 种思路是利用多天线接收到的GNSS 信号和天线的几何结构信息获得信号在载体坐标系(b系)的实际到达方向。另一方面可以通过星历信息中的卫星位置确定信号在东北天(ENU)坐标系(n系)中的理论到达方向[9]。在多天线载体姿态已知的前提下,信号理论和实际方向矢量之间可以通过姿态阵进行旋转变化。当二者不一致时,则认为存在欺骗信号[10]。在当前的技术条件下,欺骗信号几乎不可能与真实信号实现严格的相位同步,也很难提前获取用户的位置信息,因而无法模仿真实信号的到达方向[11]。该方法是当前最为强大的欺骗检测方法,能够快速检测出复杂的欺骗信号。但是该方法需要安装惯性导航系统或大规模阵列天线以实时获取姿态信息[12-13],其成本和硬件复杂度相对较高,应用场景相对受限。
使用双天线的欺骗检测方法已经有了一定的研究,该方法能够对信号来向和基线之间的夹角进行估计。但由于仅使用2 个天线,无法对信号的仰角和方位角进行准确估计。该方法存在到达角模糊度的问题,并导致存在较大的检测盲区。但当使用3 个非共线天线时,信号的来向可以唯一的确定,进而能够极大地减小检测盲区,提升整体的检测率[14]。针对传统多天线的欺骗检测方法不能检测来自多个方向的欺骗信号或成本过高的问题,本文提出了一种使用三天线的联合定姿和欺骗检测方法。传统的直接定姿法虽然方法简单,但其结果受到基线向量精度的影响[15]。为了提升基线向量的解算精度,本文使用了长度约束的基线向量估计方法。该方法假设基线长度是精确已知的,并使用基线长度对GNSS 观测解算的基线向量进行约束,以得到精准的基线向量和天线载体姿态的估计值。
根据载体的姿态和卫星的星历信息,能够得到载波相位单差的期望值。载波相位单差的观测值由接收机的输出结果得知。当不存在欺骗信号时,二者之间的残差应当服从0 均值的正态分布;当存在欺骗信号时,残差应当服从非0 均值的正态分布。本文构建了载波相位单差观测值和期望值之间误差平方和(sum of the squared errors,SSE)统计值的分布模型,并提出了合适的门限值以检测欺骗信号的存在。最后,通过模拟仿真和实验的形式,验证了本文所提方法的正确性。
本文使用3 个单频GNSS 天线实现了联合定姿和欺骗检测的功能。该方法无需惯导等任何额外的设备提供姿态信息,成本相对较低。同时,为了解决传统长度约束基线解算方法过于复杂的问题,还采用了长度约束的基线向量线性化求解方法。该方法能够在提高运算效率的同时,实现较高的基线解算精度,进而获得精准的姿态信息。同时,所构建的欺骗检测模型不依赖欺骗信号来自同一方向的假设,能够实现对复杂欺骗信号的快速检测。
1 直接定姿法


式中:e为基线在东方向上的坐标;n为北方向上的坐标;u为天方向上的坐标;下标数字为不同的基线。
b系和n系之间的坐标满足如下的转换关系:
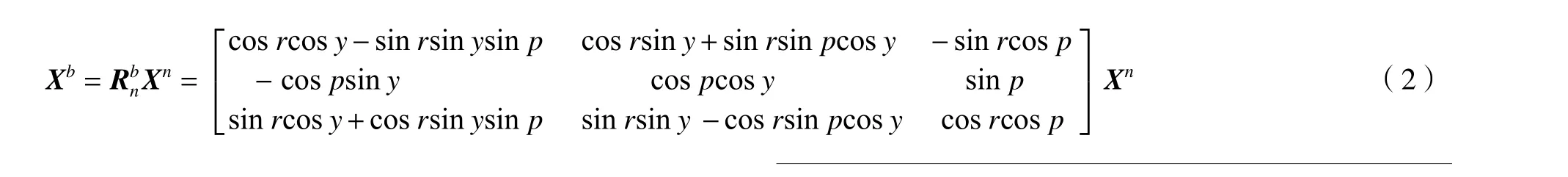



根据式(8)~式(10)可以看出,航向角、俯仰角、横滚角的精度和基线的长度、基线之间的夹角α0及GNSS 解算的基线向量精度有关。基线越长、基线向量精度越高,姿态的精度也越高。当2 个基线正交时,横滚角的误差最小。在实际的运用中,基线的长度受限于载体的面积,不可能无限制提升。因此,提高基线向量的解算质量是提升定姿精度的有效途径。但基线向量的精度会受到卫星空间分布或欺骗干扰的影响,并导致定姿结果的不准确[16]。因此,本文使用了长度约束的基线向量估计方法,使用已知的基线长度来约束基线向量的观测值,以获得高精度的基线向量估计值,进而提升定姿的精度。
2 长度约束的基线向量线性化求解法
长度约束的基线向量估计方法的有效性已经得到了充分的认证。传统的长度约束基线向量估计方法本质上是求解带二次约束的最小二乘问题,其计算效率相对较低[17]。为了提升运算速度以实现实时输出,本文构建了长度约束的基线向量线性化求解模型,能够在保持基线向量估计精度的同时,极大地提升计算效率。
基线向量解算通常采用载波相位双差观测方程进行求解,载波相位的整周模糊度采用经典的最小二乘模糊度去相关调整(least-squars ambiguity decorrelation adjustment, LAMBDA)算法固定[18-19]。以基线X12为例,本文选取最高仰角的卫星作为参考星,则载波相位双差观测方程为

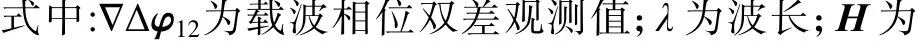

3 欺骗检测的原理
三天线欺骗检测系统的结构示意如图2 所示。三天线构成的2 个基线向量相互正交。以天线1 为原点、天线1 和2 构成的基线方向为Y轴、天线1 和3 构成的基线方向为X轴构建载体坐标系。Z轴垂直于X轴和Y轴构成的平面并满足右手坐标系。2 组基线的长度同样记作L12、L13。θ和φ分别为卫星信号i在载体坐标系的仰角和方位角。为了消除接收机钟差的影响,天线所连接的接收机采用同一振荡器驱动,以实现同步输出。根据天线之间的几何关系,卫星信号i的载波相位单差观测值可以表示为

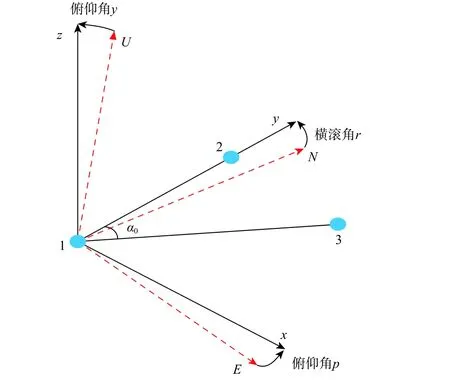
图1 载体坐标系和ENU 坐标系Fig. 1 Body coordinate frame and ENU coordinate frame
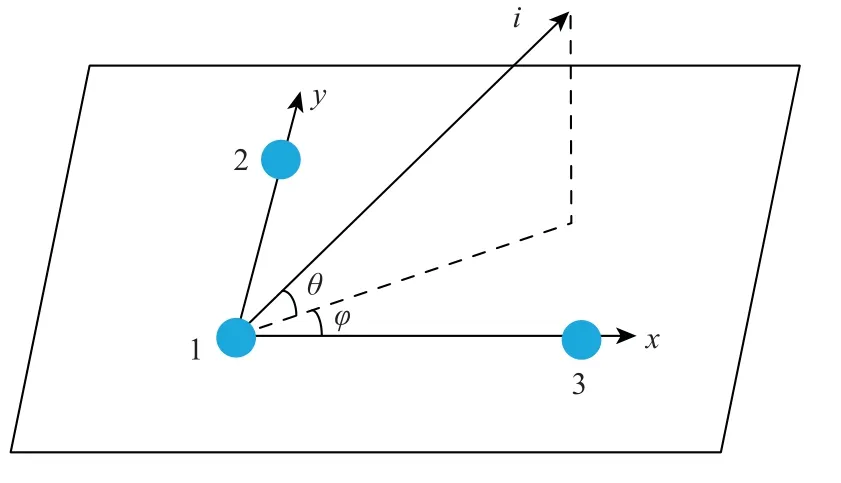
图2 系统结构示意图Fig. 2 System structure diagram

假设卫星数目为M,并且认为不同卫星的载波相位观测值是互相独立的。可以用归一化误差平方和(sum of squares of errors, SSE)统计值来评估载波相位单差观测值和期望值之间的差异:
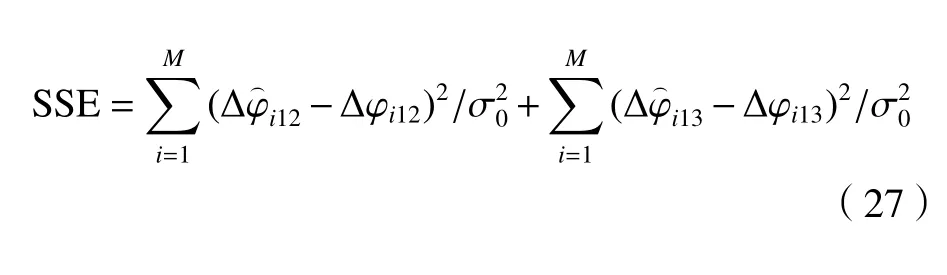

式中:Δφisp12、Δφisp13分别为欺骗信号所导致的载波相位观测值的偏移量;S为欺骗信号的数量;H0为无欺骗信号对应的统计假设;H1为有欺骗信号时对应的统计假设。根据奈曼-皮尔逊准则,本文可以通过设置适当的门限值SSEth来确定一定虚警率Pfa下的检测概率PD:
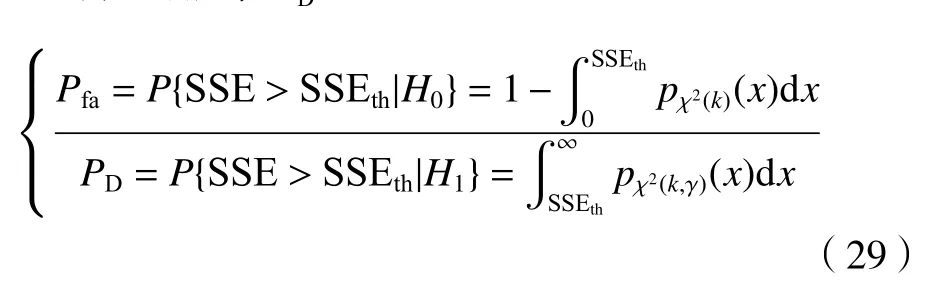
4 仿真验证

4.1 无欺骗情形

为了比较本文使用的长度约束的基线向量线性化求解法和传统长度约束方法的优劣,分别对基线向量的观测值、传统长度约束法解算的基线向量及线性化求解法所估计的基线向量进行统计,如表1所示。此外在表1 中还比较了2 种方法的计算效率。从表1 中可以看出,3 组数据均为真值的无偏估计。其均值等于基线向量的真值。另一方面,传统法和线性化法所计算的基线向量精度无显著的差异,但线性化法的计算效率大大提升。相较于传统法,线性化法所需的计算时间降低了76.2%。因此,线性化法能够在保持高精度基线解算的同时,显著提升运算效率。
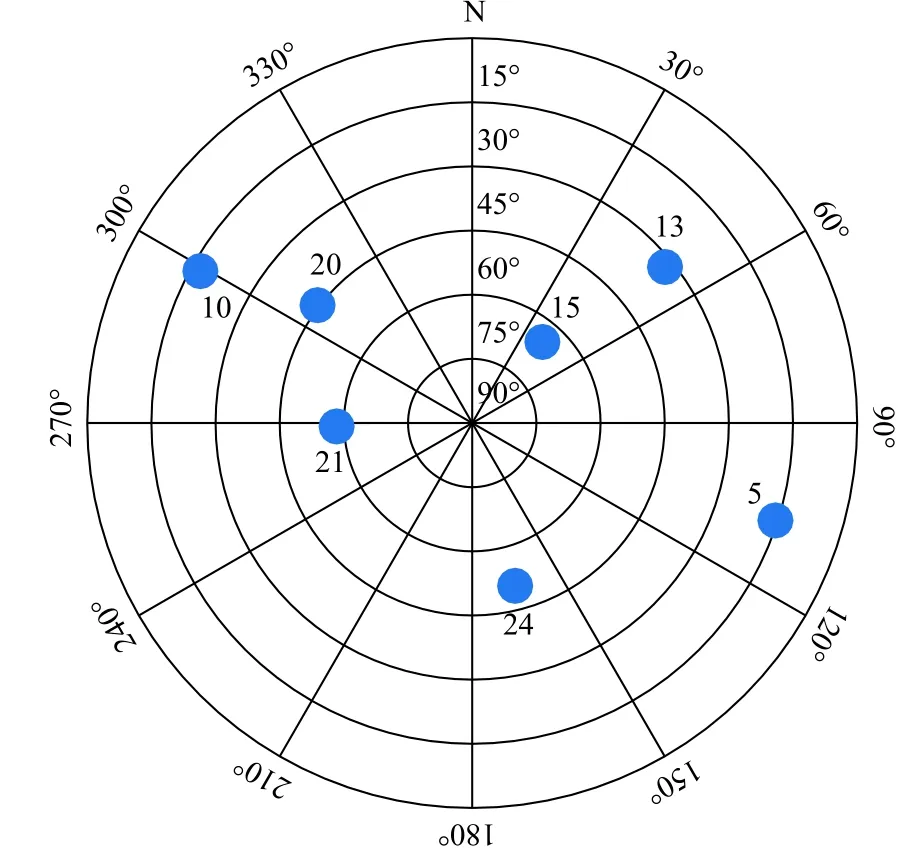
图3 ENU 坐标系下的卫星分布Fig. 3 Satellite distribution in ENU coordinate system

图4 ENU 坐标系下的基线向量观测值和估计值Fig. 4 The observed and estimated values of baseline vector in ENU coordinate system

表1 基线向量解算结果的统计量Table 1 Statistics of baseline vector solution results
同时,基线解算垂直方向的标准差明显要比水平方向要高,这与经验结果是完全一致的。由于地球的遮挡,地面上的用户只能观测到天空一侧的卫星,造成垂直方向上的误差传播要大于水平面上的误差传播。相较于观测值,线性化法估计值的标准差明显地降低。标准差在ENU这3 个坐标轴上分别降低了74.2%、76.1%和78.7%。
采用直接定姿法分别计算基线向量观测值和线性化法的估计值对应的姿态角,姿态角的误差分布如图5 和表2 所示,航向角,俯仰角和横流角的标准差分别降低了76.1%、79.2%和78.8%。可以看出,姿态角的结果同样具有无偏性。根据GNSS 定姿理论,1 m 长基线对应的姿态角的标准差大约为0.6°[20]。该结论与基线向量观测值对应的姿态角标准差完全一致。

图5 姿态角的误差Fig. 5 Error of attitude angle
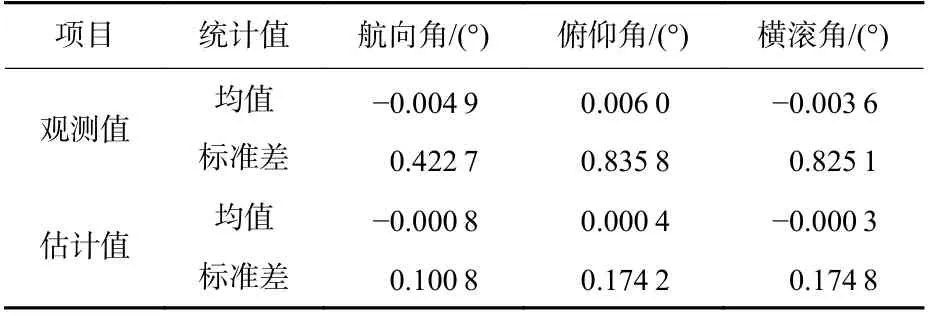
表2 姿态角误差的均值和标准差Table 2 Mean and standard deviation of attitude angle error
和观测值相比,基线向量估计值所对应姿态角误差的均值更接近0,且标准差显著降低。这表明本文使用的长度约束的基线向量估计方法能够有效地提升直接定姿法的精度。另一方面也可以看出,航向角的精度明显要高于俯仰角和横滚角。根据式(8)~式(10)可以得知,航向角的精度仅和基线的水平分量有关,而俯仰角和横滚角还和基线的垂直分量有关。基线垂直分量的精度直接导致了俯仰角和横滚角精度的降低。
当姿态角确定以后,根据卫星在ENU坐标系下的仰角El和方位角Az,可以求出卫星在载体坐标系下的仰角θ和方位角φ,进而求出载波相位单差的期望值 Δφi。载波相位单差的观测值 Δφ⌒i和期望值 Δφi之间的SSE 统计值如图6 所示。SSE 统计值的概率密度分布和理论分布χ2(14)之间存在微小的偏差,该偏差是由于定姿误差所导致的。本文使用R方值评估SSE 统计值和理论分布函数之间的拟合程度。R方是拟合优度指标,R方的取值范围为0~1,R方越接近1,则认为拟合效果越好[21]。
通常R方大于0.8 就表明拟合度很高。图6 中对应的R方值为0.864,因此,笔者认为χ2(14)是SSE 统计值非常有效的分布拟合。根据式(29),可以设置门限值SSEth=50,则对应的理论虚警率为1.1×10-5。SSE 统计值的真实虚警率为pfa=3×10-4。考虑到噪声的影响,虚警率与理论值基本一致。

图6 SSE 统计值的概率密度分布Fig. 6 Probability density distribution of SSE statistics
4.2 有欺骗情形
欺骗信号由于其功率高于真实信号,能够夺取接收机的跟踪环路,进而导致载波相位的观测值产生偏差。在有欺骗的情形中,本文为SV13 和SV21两颗卫星的载波相位值引入偏差,以模拟2 个转发式欺骗信号源分别转发一路欺骗信号的场景。2 个欺骗源和真实信号在载体坐标系中的仰角和方位角偏差均为-10°,其他参数与无欺骗情形完全一致。真实信号和欺骗信号在载体坐标系下星座分布图如图7 所示。
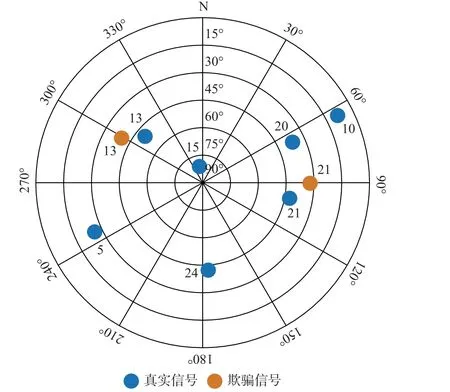
图7 载体坐标系下的卫星分布Fig. 7 Satellite distribution in body coordinate system
有欺骗信号时的姿态角误差的概率密度分布和统计值如图8 和表3 所示。从图8 中可以很明显地看出,由于存在欺骗信号,基线向量观测值对应的姿态角产生了很大的误差,不再具有无偏性。航向角、俯仰角和横滚角误差的均值分别为7.48°、-2.66°和9.07°。标准差和无欺骗情形基本一致。
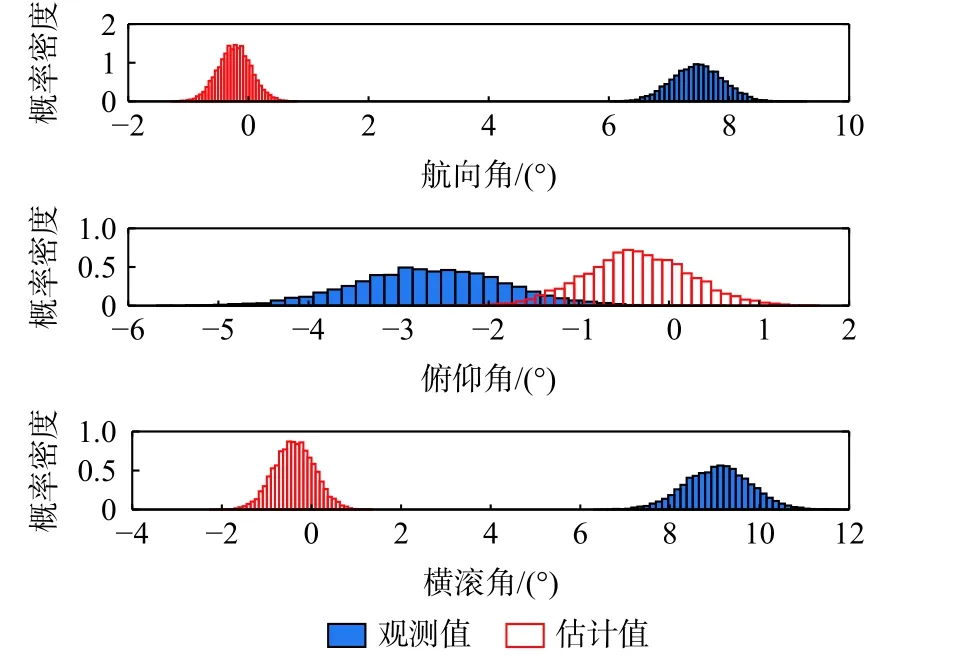
图8 有欺骗信号时姿态角误差的概率密度分布Fig. 8 Probability density distribution of attitude angle error with spoofing signals
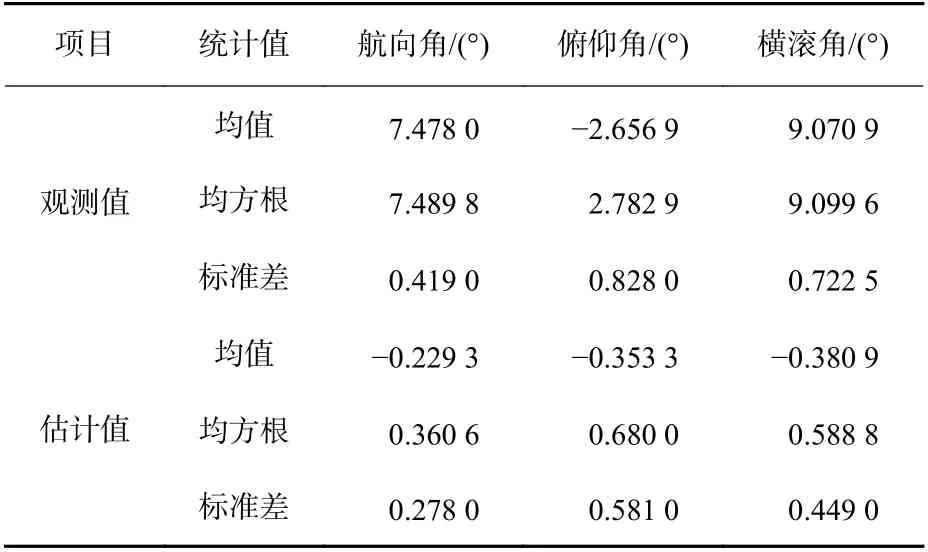
表3 有欺骗信号时姿态角误差的统计值Table 3 Statistical values of attitude angle error with spoofing signals
基线向量估计值所对应的姿态角同样不是无偏的。相较于观测值,估计值所对应姿态角误差的均值大幅度降低了。航向角、俯仰角和横滚角误差的均值分别为-0.229°、-0.353°和-0.381°。同时,姿态角的均方根误差和标准差均显著降低了。标准差分别降低了33.7%、29.8%和37.9%。由于欺骗信号的影响,估计值所对应姿态角标准差相较于无欺骗情形明显提升。俯仰角和横滚角的标准差要高于航向角,与无欺骗的情形一致。本节结果表明,即使存在欺骗信号的干扰,本文使用的长度约束的基线向量估计方法也能够得到较为精准的姿态角信息。
根据式(25)、式(26)和式(28)可以得到H1假设所对应的理论分布函数χ2(14,γ)。SSE 统计值的概率密度分布如图9 所示。与图5 相比较可以看出,有欺骗信号时的SSE 统计值要超过无欺骗时2 个数量级。因此,通过SSE 统计值可以很轻易地分辨出是否存在欺骗信号。根据上文设置的SSEth,检测率pD=100%。由于欺骗信号的干扰,SSE 统计值和理论分布函数χ2(14,γ)之间的误差增大,二者之间的R方值为0.802。相较于无欺骗情形,R方值降低,但依然大于0.8。

图9 有欺骗信号SSE 统计值的概率密度分布Fig. 9 Probability density distribution of SSE statistics with spoofing signals
5 实验验证
为了验证本文所提方法的性能,在中国科学院空天信息创新研究院开展了欺骗检测实验。使用北斗星通UB482 接收机板卡搭建了三天线的定姿和欺骗检测系统。北斗星通UB482 接收机能够对多天线同步驱动以消除天线之间的钟差,UB482板卡实物图如图10 所示。实验使用同型号、同批次的天线,以消除可能的传输延迟和相位中心偏差。采用GNSS 转发器作为欺骗源,转发器型号为Gemsnav RGA30-DV。转发放大器的实物图如图11所示。

图10 UB482 接收机实物图Fig. 10 Physical picture of UB482 receiver

图11 RGA30-DV 转发放大器Fig. 11 Physical picture of RGA30-DV repeater amplifier
基线的长度L12、L13同样为1 m。本文提前进行了30 min 持续无欺骗的观测,并取定姿结果的均值作为天线载体姿态的真值为y=-62.1°、p=-1.2°、r=1.8°。欺骗场景的测试时间为200 s,接收机输出频率为1 Hz。欺骗源转发一路GPS 信号并对真实信号造成干扰。和模拟的场景类似,本文分别计算了基线向量观测值和长度约束后的估计值所对应的定姿结果。姿态的3 个欧拉角随时间变化趋势如图12 和图13 所示。由于存在欺骗信号,导致图12 中的定姿结果存在大量的散点。对比2 幅图可以看出,图13的定姿结果非常稳定,波动幅度很小。
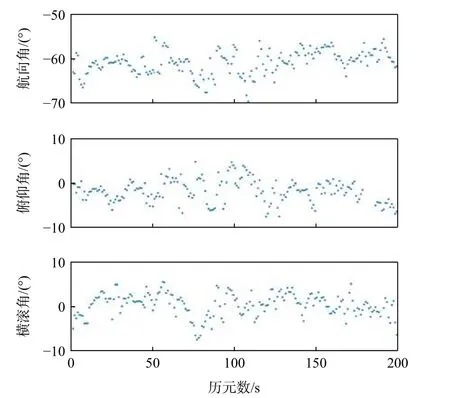
图12 基线向量观测值的定姿结果Fig. 12 Attitude determination results of baseline vector observations

图13 基线向量估计值的定姿结果Fig. 13 Attitude determination results of baseline vector estimation
2 组定姿结果的3 个欧拉角统计值如表4 所示。从表4 中可以看出,基线向量观测值的定姿结果的均值和真值产生了较大的偏差,3 个欧拉角的均值分别产生了1.79°、1.01°、2.1°的偏差。而估计值的定姿结果均值分别产生了0.18°、0.12°、0.06°的偏差。即使存在欺骗信号的干扰,估计值的定姿结果与真值也非常接近。同时还可以看出,估计值的定姿结果的标准差相较于观测值分别降低了86.7%、77.3%和88.2%。航向角的精度要略高于其他2 个姿态角,和模拟的结果完全一致。

表4 姿态角均值和标准差Table 4 Mean and standard deviation of attitude angle
欺骗场景的SSE 统计值随时间变化趋势如图14 所示。欺骗场景的SSE 统计值要远远大于门限值,检测率达到了100%。和图9 模拟的结果进行比较可以看出,由于实验场景仅存在一个欺骗信号,因而SSE 统计值要小于模拟场景,但也高于门限值一个数量级。
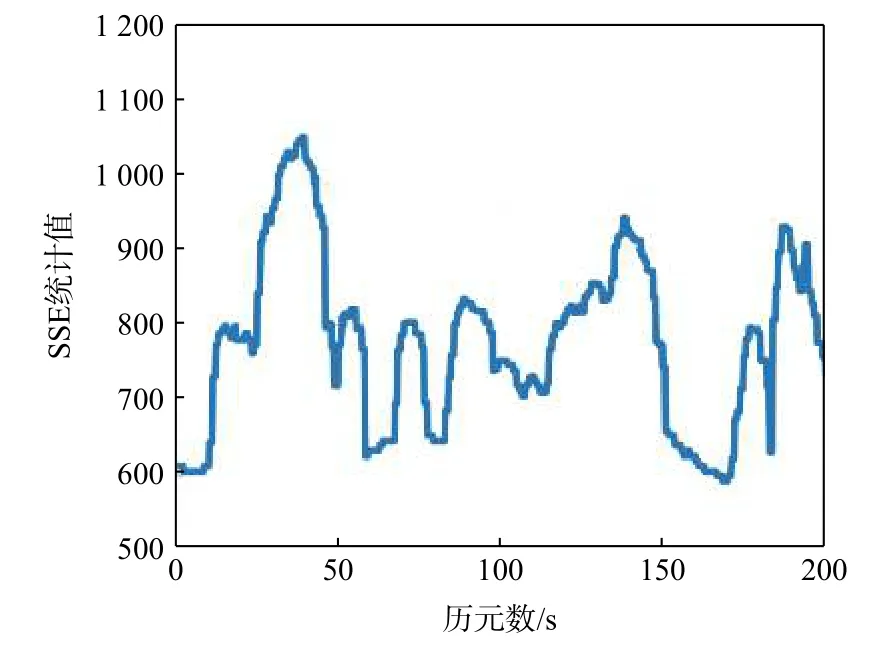
图14 欺骗场景的SSE 统计值Fig. 14 SSE statistics in spoofing scenario
6 结 论
1) 本文所提方法能够有效提升基线向量的精度。模拟结果表明,所提方法能够实现无偏估计,同时,基线向量在东北天3 个坐标轴的标准差分别降低了74.2%、76.1%和78.7%。所提方法能够提升传统的直接定姿法的精度。航向角、俯仰角和横滚角的标准差分别降低了76.1%、79.2%和78.8%。
2) 本文所提方法的虚警率和理论虚警率保持一致。
3) 实验结果表明,在有欺骗信号存在的情形,本文所提方法能够实现100%检测率,且能够降低姿态角的误差77.3%以上。
4) 本文提出了欺骗检测的二元检验理论分布模型。模拟和实验结果表明,该模型具有较高的可用性。
