无人机自主引导跟踪与避障的近端策略优化

2023-02-09胡多修董文瀚解武杰

北京航空航天大学学报 2023年1期

胡多修，董文瀚，解武杰

(1. 空军工程大学研究生院，西安 710038； 2. 空军工程大学航空工程学院，西安 710038)

多旋翼无人机具有结构简单、机动性强、安全性高等特点，使其成为计算机技术、智能控制技术、微机电系统传感器技术等多学科领域融合研究的理想平台。近年来，随着计算机视觉和人工智能技术的逐步成熟，基于多旋翼无人机的地面动目标跟踪成为了研究热点[1-2]。无人机自主化、智能化的任务处理能力是完成上述研究的关键技术，也是当今无人机的发展趋势[3]。

传统无人机飞行引导控制方法，如PID 控制、滑模控制、模型预测控制和自适应控制等，根据控制理论设计轨迹跟踪控制器，通过对应飞航迹的跟踪，达到引导无人机飞行的目的。这类控制器通常针对静态目标或者已知航迹的飞行任务。对于未知运动规律的对地侦察任务机动策略的设计方法，目前主要分为基于对策的决策算法（如矩阵对策法[4]、影响图法[5]）和基于人工智能的决策算法（如遗传算法[6]、深度学习算法[7]等）。尤其是深度学习在物体分类、物体检测等任务中表现出了非常优异的性能，因而得到广泛应用[8-11]。然而上述算法也在一定程度上存在着局限性，如矩阵对策法的算法计算量大、结果精度低，响应图法建模过程复杂、求解计算量大。智能算法虽然无需复杂的建模过程，但遗传算法容易陷入局部最优，且算法复杂度高，难以满足无人机自主决策的实时性要求，深度学习需要已知的飞行数据及投入较高的时间成本。

强化学习是机器学习的一条分支，其本质是智能体感知环境，同时利用评价性的环境反馈信号来优化所采取的行为策略[12]。优化方法主要分为基于值函数的方法和基于策略的方法。基于值函数的方法适用于离散动作空间，策略改进时，需要针对每个状态行为对求取行为值函数，以便求取最优解，但在无人机机动这类状态空间很大的连续动作集问题中，基于值函数的方法便无法有效求解了。研究者们提出了基于策略的解决方案，其中，近端策略优化（proximal policy optimization，PPO）算法有效解决了传统策略梯度算法中学习步长难以确定的问题，并在连续状态空间上得到了应用[13-15]。

在指定的任务空间内，对于静态目标而言，实际上解决的是无人机定点引导问题。文献[16]采用视觉引导的方法，提出一种轻量高效的Onboard-YOLO 算法，实现了无人机的实时精准降落，但未考虑动态靶标的降落问题；文献[17]利用深度确定性策略梯度（deep deterministic policy gradient, DDPG）算法实现了无人机对动态目标的持续跟踪，但缺乏无人机高度变化时的机动策略，并且没有提出对突发情况[18-19]（禁飞区、障碍物等）的解决方案。

本文基于深度强化理论，提出无人机自主引导与跟踪避障的机动控制方法。首先，基于马尔可夫决策过程（Markov decision process, MDP）理论设计自主引导模型与伴飞避障模型；然后，针对上述模型设计相对应的PPO 网络结构；最后，通过基于ROS、GAZEBO、PX4 的3D 仿真试验平台进行验证[20-22]。经过试验分析，本文提出的设计方法具有很高的合理性，有效实现了侦察任务全过程的自主机动。

1 问题描述

无人机在跟踪地面目标时，初始距离难以掌控，往往需要远距离自主引导和近距离伴飞跟踪2 个阶段共同完成整个侦察任务。

1.1 远距离自主引导过程

1.2 近距离伴飞避障过程

当无人机与目标的相对位置关系达到阈值时，侦察任务进入伴飞避障阶段。假设禁飞区Onfz的空间位置为Pnfz，最大距离为Dnfz，最小安全距离为dnfz。为了简化模型，采用禁飞区外截圆模型代替本身的不规则区域，并设置大小可调的安全距离

无人机、目标及障碍物的相对位置关系如图2所示。这一阶段的环境复杂度相对较高，考虑无人机如何在定高空域快速接近目标的同时，更要兼顾禁飞区、障碍物等诸多不利因素对侦察任务造成的威胁，通过设计合理的机动策略，可以实现规避障碍、持续跟踪的目的。

图2 障碍物、目标与无人机的空间位置关系Fig. 2 Relative position of obstacle, target and UAV

2 地面目标跟踪系统建模

2.1 马尔可夫决策过程模型

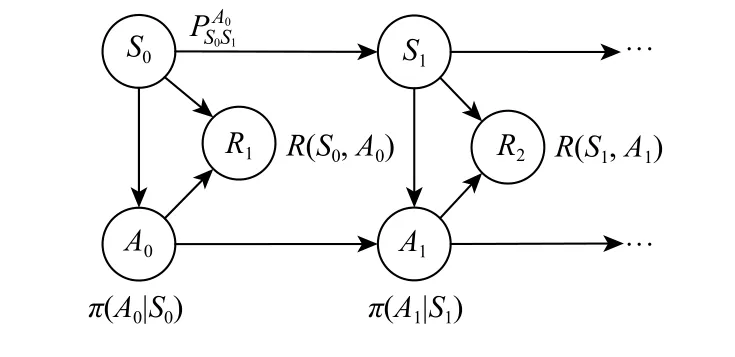
图3 马尔可夫决策过程模型的描述Fig. 3 Description of Markov decision process model

2.2 基于位置和速度信息的无人机机动模型

2.2.1 自主引导模型

2.3 地面目标随机运动模型

3 无人机目标跟踪方法

针对无人机自主侦察任务2 个阶段不同的任务需求，设置相互独立的子任务环境并进行单独训练，完整的方法流程如图4 所示。

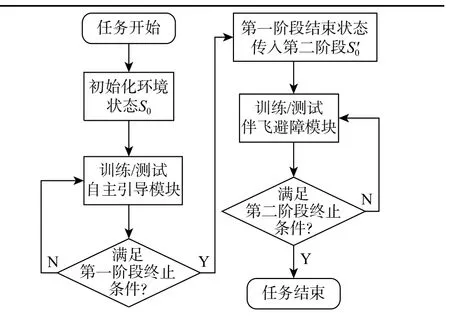
图4 自主引导与伴飞避障流程Fig. 4 Flowchart for autonomous guidance and obstacle avoidance of accompanying flight

强化学习任务中，可以通过建立状态值函数估计，也可以直接建立策略的估计来解决一系列问题，根据估计方法的不同，强化学习方法可以分为基于值函数的方法、基于策略的方法及行动者-评论家（actor-critic，AC）方法。本文采用的PPO 算法延续了置信域策略优化算法的步长选择机制[23]，借鉴了基于策略的方法的估计思想，继承了AC 算法中策略与价值双网络的经验[24]，算法的基本框架如图5 所示。

图5 中，环境为无人机与地面目标构成的任务空间，行动者网络生成策略，评论家网络通过估计优势函数An来评估并改进当前策略，二者都是根据策略梯度进行优化，且行动者网络参数 θA、评论家网络的参数 φC的更新公式如下：

图5 PPO 算法框架Fig. 5 Structure of PPO algorithm

3.1 PPO 训练框架

其中： ε为超参数。

行动者网络根据当前状态sn产生控制信号an，无人机执行动作产生状态sn+1并获得奖励rn，经验回放集合将上述信息打包为一组 {sn,an,rn,sn+1}并进行存储，最终用于更新网络参数，获得相对最优策略。

输入：初始化行动者网络参数 θ0A、评论家网络参数 φ0C，初始化记忆库容量R。

对于每一条轨迹， for episode=1,...,M：初始化环境，得到S1;

对于轨迹中的每一步， forn=1,...,N：根据策略an=πθA(Sn) ，执行行为an；获得回报rn和下一个状态Sn+1；将状态转换序列(Sn,an,rn,Sn+1)存入记忆库中；更新状态Sn=Sn+1；计算优势函数An；

每执行L步

通过计算策略梯度 ∇θALclip(θA)，更新行动者网络参数 θA；通过计算策略梯度 ∇φCL(φC)，更新评论家网络参数 φC；更新参数 θAold=θA；

单条轨迹循环结束

M条轨迹循环结束

输出：最优网络参数： θA*及最优策略 π*。

算法中有2 个结构相同的行动者网络，一个生成待优化的策略 πθA(an|sn)，另一个 πθAold(an|sn)用于收集数据，并通过重要性采样来估计新策略，更新过程中，PPO 算法利用式(32)的损失函数限制了πθA(an|sn)的更新幅度，确保新旧策略的偏离程度不会太大。

3.2 网络结构及参数

3.2.1 LSTM 循环神经网络结构

长短期记忆（long short-term memory，LSTM）网络应用于输入数据是序列模式且具有依赖性时的场景[25-26]，在目标跟踪任务中，无人机接收到的数据具有时序性且环境状态存在上下文关联，使得LSTM网络能够很好地满足任务需求[27]。将LSTM 与深度强化学习算法相结合并应用于无人机侦察任务，其本质就是将目标运动轨迹等状态信息作为输入，当前时刻无人机对应的机动控制信号作为输出，计算奖励值，更新网络参数，并通过自适应优化算法反复迭代得到最终模型。

LSTM 框架[28]的循环单元由4 部分组成：遗忘门f、输入门i、输出门o及记忆单元C。图6 展示了LSTM 中每一个单元的计算细节。

图6 LSTM 结构示意图Fig. 6 Schematic of LSTM structure

3.2.2 LSTM 循环神经网络参数设置

1）数据归一化处理。为了减小因输入的特征数据间数量级差别较大引起的模型误差，并使不同维度的特征在数值上有一定的比较性，需要对输入的特征参数作归一化处理。针对无人机目标跟踪的2 个阶段，采用转换函数将原始特征数据转换成取值范围在[ 0,1]之间的数据。其中，对自主引导模型的行动者网络输入层参数进行非线性变换，利用 sin(.)、cos(.)函数将 σn进行分解，利用 t anh(.)函数限定参数 σ˙n、Ln，参数 τn不变。伴飞跟踪模型的行动者网络输入层由PTnAG-PUnAV、Pnnfz-PUnAV及VnTAG-VnUAV通过矢量分解而来，对输入层参数作线性变换，转换函数如下：

式中：X为特征数据；X*为归一化后的特征数据。

自主引导模型与伴飞跟踪模型的行动者网络输出无人机速度控制信号，且均采用 tanh(.)函数实现输入量与输出量的归一化。

评论家网络用于计算优势函数以评估并改进当前策略，输入层参数为状态S与动作A的集合，其网络结构与输入层参数的归一化方法与行动者网络相同，不同之处在于输出量并未做归一化处理，直接参与损失函数计算。

2） LSTM 隐藏层神经元个数选择。隐藏层能够把输入数据的特征抽象到另一个维度空间，从而进行更好地线性划分，隐藏层的神经元个数对网络的拟合能力有着很大的影响，神经元个数不足会降低网络的拟合能力，达不到预期的预测精度，而神经元个数过多则会造成网络过拟合或者徒增训练时长，因此，根据任务要求，合理选择隐藏层的神经元个数非常重要。本文所涉及的实验内容选择了256 个隐藏层神经元。

4 模型验证及分析

4.1 试验方案

选取3 类任务场景验证模型的可靠性：场景1采用自主引导模型，场景2 采用伴飞避障模型，场景3 则通过设置阈值（无人机高度为10 m，无人机与目标相对距离不大于20 m）将2 个模型规整到同一任务流程中，并分别将场景1 和场景2 收敛后的模型训练网络运用于全过程。上述3 类场景所对应的模型训练参数如表1 所示。基于上述场景，分别将基于传统PPO 算法和本文提出的基于LSTM网络的PPO 算法设置为对照组，隐藏层神经元个数均设置为256，并采用相同的参数优化器对模型训练参数进行更新。

表1 仿真参数设置Table 1 Simulation parameter setting

4.2 试验结果与性能分析

通过不同场景中无人机单步平均奖励曲线的变化情况，定量评估传统PPO 算法与基于LSTM网络的PPO 算法在无人机自主机动这类任务中的实时性、准确性和鲁棒性。

假设无人机的状态信息和输出量均为无偏信号。由图7（a）可见，场景1 中由改进后的PPO 算法训练的无人机单步平均奖励初始值为-8.8，并在训练轮数达到250 次时稳定在-2.6。传统PPO 算法训练的无人机单步平均奖励初始值为-11.1，训练轮数达到325 次时逐渐收敛于-7.5。场景2 的环境复杂度相对较高，试验所设置的环境奖励力度较大，由此导致初始累计奖励较低，如图7(b)所示，改进后的PPO 算法训练的无人机单步平均奖励初始值为-69，训练轮数达到400 次时稳定在-8，而传统PPO 算法训练的无人机单步平均奖励初始值为-78，训练轮数达到600 次时收敛至-42。在实际的侦察任务中，气流等环境因素的变化使得无人机系统的状态信息存在一定的偏差，本节通过给输出量叠加其自身0.2 倍的噪声信号以模拟无人机系统状态的不稳定性。由图7（a）可见，由于干扰信号的存在，改进后的PPO 算法训练的前75 次无人机单步平均奖励值出现下降趋势，但随着训练的进行，干扰信号带来的影响逐渐减弱，并在训练轮数达到250 次时，奖励值收敛至-3。传统PPO 算法训练的无人机单步平均奖励值出现较大波动，且训练轮数达到350 次时逐渐收敛于-11。类似的现象也出现在图7（b）中，干扰出现后，改进后的PPO 算法收敛速度略微降低，但整体处于上升趋势，并在训练轮数达到450 次时，无人机单步平均奖励值稳定在-10。传统PPO 算法训练的无人机单步平均奖励涨幅不明显，训练轮数达到650 次时收敛于-60。图8 为基于传统PPO 算法训练下的自主引导模型与伴飞避障模型的无人机飞行轨迹。由图8（a）可见，无人机执行引导过程且引导结束时，无人机与地面目标的距离相对较远，引导效果较差。如图8（b）所示，无人机执行伴飞避障过程，当环境状态发生变化时，无人机能够有效进行避障，确保无人机的飞行安全，但无人机跟踪性能显著下降，导致侦察任务失败。如图8（c）所示，结合场景1 与场景2 进行自主引导与伴飞避障全过程验证，由于传统PPO 算法训练下的自主引导模型效果较差，为避免终止时间条件内，无人机无法达到模型切换阈值，本文放宽了阈值条件。仿真结果表明，无人机进行第一阶段的机动决策耗时较长，导致第二阶段进行避障后，无法在所设置的终止时间内对地面目标重新跟踪。

图7 单步平均奖励变化曲线Fig. 7 Variation curves of single step average reward

图8 不同场景下基于传统PPO 算法的运动轨迹Fig. 8 Motion paths in different scenarios based on traditional PPO algorithm

图9 为基于改进后的PPO 算法训练后的无人机飞行轨迹。由图9（a）可见，无人机与地面目标初始相对距离较远时，自主引导模型有效作用，二者相对距离迅速减小且无人机高度逐步下降。如图9（b）所示，无人机与地面目标初始相对距离较近时，伴飞避障模型有效作用，无人机与侦察目标的相对高度保持不变，在定高空域执行侦察任务。图9（c）则结合了场景1 与场景2 中各模型的优势，自主引导阶段完成时，无人机迅速转变机动策略，接近目标的同时兼顾了可能出现的低空威胁，进行了合理有效的避障跟踪。

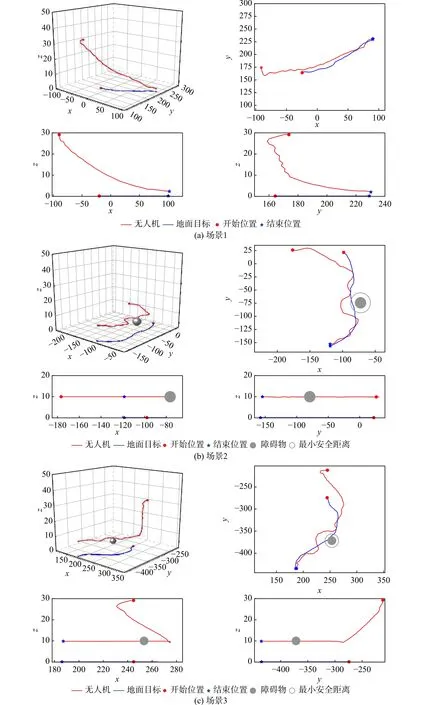
图9 不同场景下基于改进PPO 算法的运动轨迹Fig. 9 Motion paths in different scenarios based on improved PPO algorithm

上述结果表明，无人机自主引导与伴飞避障过程是合理的，且相较于传统神经网络， LSTM 网络拥有独特的记忆单元结构，地面目标的历史轨迹属性在训练时就已经存入隐藏层记忆细胞内，对地面目标进行下一轮跟踪时，可以迅速找到相应的细胞状态。当目标出现新的轨迹属性时，LSTM 网络的遗忘门会清除较旧的上下文轨迹信息，并通过状态更新将新的目标位置信息添加到细胞状态中。因此，基于LSTM 网络的PPO 算法具有更强的实时性、准确性和鲁棒性。