卷积线性混合模型下的复非高斯信号盲源提取

李苗苗，吕晓德，王宁，刘忠胜

(1. 中国科学院空天信息创新研究院，北京 100094； 2. 微波成像技术国家级重点实验室，北京 100190；3. 中国科学院大学，北京 100049)

单个雷达发射信号一般具有特定的波形、幅度和相位变化规律，并不具有随机性，为非高斯信号，其在传播过程中，由于受到周边环境的影响，会产生多径。目前，发展较为成熟的盲源分离算法一般将混合系统建模为瞬时线性混合模型，当处理具有多径现象的混合源时，将各个发射基站的每个多径信号看作一个独立的信号源，而该类算法通常要求接收通道数量大于或等于源信号数量，导致接收通道需求量大，复杂的分离情况还可能导致盲源分离效果不佳，进而不能准确提取出想要的目标信号。另外，在实际测量过程中，由于受到干扰尤其是恶劣环境的影响，使得目标信号淹没在强干扰之中，造成雷达信号目标检测能力大幅下降。因此，如何在低信干比的情况下提取出想要的目标信号，也是雷达信号处理领域比较关注的问题，这些都给在高斯背景中的复非高斯微弱信号提取问题带来挑战。

针对多信号盲源分离问题，目前已有大量研究工作，学者们也根据不同角度提出了很多有效的算法。其中，独立分量分析（independent component analysis, ICA）是Comon 于1994 年针对盲源分离问题提出的一种开拓性方法[1-2]，其目的是通过互信息最小化或者负熵最大化等准则将混合系统中的各混合信源分离开。随着学者们对该方法研究的深入，尤其是快速独立分量分析（FastICA）算法[3-4]的出现使得计算效率大幅提高，该方法也逐渐被应用在生物医学、语音、图像处理、雷达信号处理等领域，近年来，学者们在利用ICA 方法进行雷达信号同频干扰抑制[5-8]、多信号分离及滤波[9-11]、图像及混合信号去噪[12-15]等方面取得了一些成果。文献[5-6]将ICA方法应用到雷达信号同频干扰抑制上，利用ICA 方法在时域上提取出与同频干扰相互重叠的目标信号，从而达到抑制同频干扰的目的；文献[11]利用FastICA 算法作为一种自适应滤波方法，通过对线性混合在高斯噪声中的多正弦信号进行滤波，验证了该方法的滤波能力；文献[12]提出了一种基于FastICA 的低信噪比探地雷达信号去噪方法，仿真实验了FastICA 算法对混合在探地雷达数据中的高斯白噪声、脉冲噪声及阶跃噪声的去噪处理，得到了不错的效果。上述研究将ICA 应用在雷达同频干扰抑制及信号去噪方面，但使用的仿真模型均为瞬时线性混合模型，未考虑实际场景中的多径传播问题，并且对于复数情况下的处理未做详细说明。文献[16]考虑了信号在实际传播中的多径问题，提出一种基于二阶循环平稳统计的卷积混合盲源提取方法，并用仿真结果验证了该方法的有效性，但必须要求感兴趣源具有唯一的循环平稳频率，才可以将其从实测数据中有效地恢复出来；文献[8]针对无源雷达中的同频干扰问题，在卷积混合模型下提出一种基于二阶统计量的盲源分离算法，利用了源信号的非平稳特性，通过分离同频干扰直达波和多径杂波来抑制同频干扰，但是该方法对于单高斯场景下的盲源分离问题并无显著优势，这是因为呈高斯分布的随机信号的高阶统计量为零，所以基于高阶统计量的盲源分离算法与基于二阶统计量的盲源分离算法相比具有天然的抗高斯特性；文献[10]考虑到眼动“源”与外部观测信号之间的传播路径问题，为寻找一种能够有效分离眼跳运动信号的盲源分离模型，针对瞬时和卷积混合2 种盲源分离模型进行了多通道眼电图信号分离对比实验，实验结果表明，卷积混合模型分离出的眼跳信号质量比瞬时模型分离出的眼跳信号质量高，体现了卷积混合模型对于该场景的分离优势。

综上所述，基于高阶统计量的盲源分离算法具有天然的抗高斯特性，可以在混合源中对高斯信号实现有效去除，但是信号在传播过程中普遍存在多径现象，若不考虑此现象，可能会出现盲源分离类算法对接收通道数量需求大、分离复杂导致性能不佳等问题，同时由于大多数实用的调制形式都是复数类型，复值信号经常出现在通信、雷达、生物医学等应用中，相应的处理也需要在复数域进行，使得信号的完整信息得以充分利用[17]。本文同时考虑了雷达信号实际处理中存在多径传播及算法对复值信号的处理问题，提出一种基于卷积线性混合模型的复非高斯信号盲源提取方法。将混合系统建模为卷积线性混合系统，更改了复数FastICA 算法中观测向量和权值向量的构造方式，与瞬时线性混合系统相比，大大节约了接收通道数量，通过利用基于高阶统计量的FastICA 算法在强高斯干扰背景中对非高斯信源的提取优势，即使在极低的信干比情况下也能在混合信源中成功提取出复非高斯信号，从而达到微弱信号提取或去噪的效果，并通过仿真实验验证了该方法的有效性。

1 卷积线性混合模型

2 非高斯信源提取

若混合信源中具有非高斯信源，则对其进行提取需作出如下假设：

1) 所提取的信号必须是非高斯信号。

2) 接收数据通道数大于或等于2。

3) 混合矩阵H(z) 为m×n维的FIR 多项式矩阵，且H(z)的秩对每个非零的时延列满秩。

若要对卷积混合信源中的非高斯信源进行提取，提取向量的设计尤为关键。由于H(z)是完全未知的，W(z)H(z) =I不可实现，于是将设计目标松弛为[2]

式中：G(z) =[g1(z),g2(z)...,gn(z)]∈Cn×n为广义交换FIR 多项式向量。

对于单路源信号的提取，可以表示为

令解混合矩阵的最大阶次为K（K应该大于或等于混合FIR 滤波器的阶次L），单个解混合FIR 滤波器的表达式为

为了方便对比卷积线性混合模型与瞬时线性混合模型的异同，写出瞬时线性混合模型的单个分离信号的具体表达式，如下：

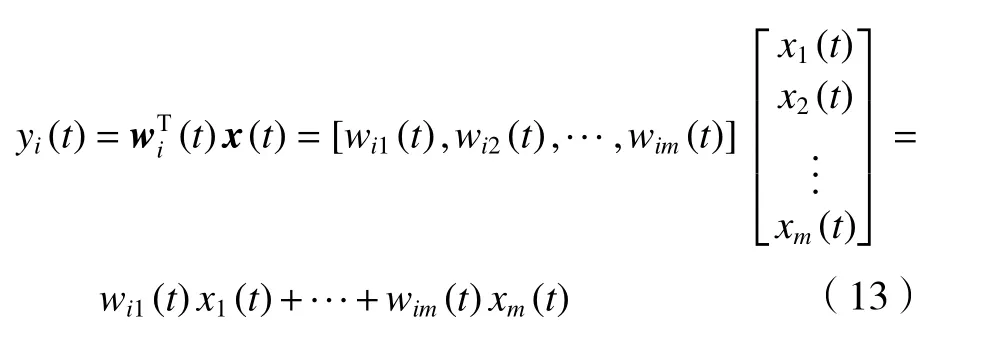
通过对比式（12）和式（13）可以看出，卷积线性混合模型与瞬时线性混合模型的盲信号分离不同之处在于解混合向量和观测向量的选取。在卷积线性混合模型中，解混合向量和观测向量的选取分别如式（14）和式（15）所示，本文的目的则是通过求式（14）来提取混合源中的复非高斯信号。

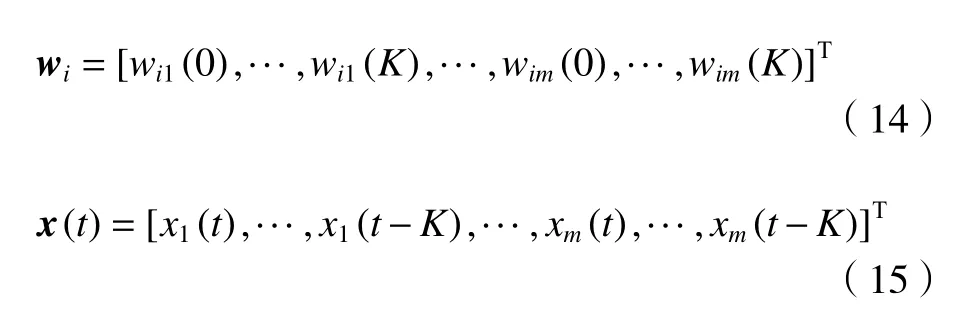
假设单个或多个复非高斯信号与复高斯干扰信号卷积混合，通过2 个信道接收，未知源信号混合方式及复非高斯信源的提取过程如图1 所示。将复非高斯信源看作混合系统的一路输入，复高斯信源看作另一路输入，则需要4 个混合FIR 滤波器，各信源经过不同的混合滤波器之后再线性叠加得到2 组观测数据，使用复数FastICA 算法从2 组观测数据中提取复非高斯信源。信干比定义如下：

图1 复非高斯信源提取模型Fig. 1 Complex non-Gaussian source extraction model

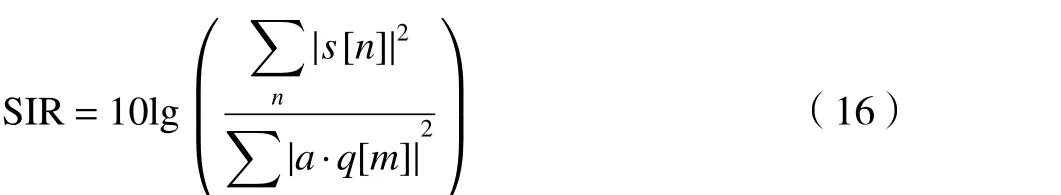
3 复数FastICA 算法

为了实现复非高斯信号的盲源提取，本文使用了复数FastICA 算法。在高斯背景下，该算法表现出良好的分离性能，能够很好地避免局部最优问题，当除了感兴趣源外没有其他非高斯分量时，具有很好的全局收敛性[18]。由于高斯信号没有高于二阶的统计量，基于高阶统计量的FastICA 算法具有天然的抗高斯特性，通过利用输出信号高阶累积量的最大化实现去高斯化，从而达到从混合信源中提取出非高斯微弱信号的目的。

为了实现独立分量分析，FastICA 算法衡量信号向量各分量之间统计独立性的测度是负熵，当信号各分量负熵达到最大时，可认为将混合信号完全分离[2]。设信号向量为：y=[y1,y2,...,yn]T，其微分熵的表达式为[3]

步骤 3 循环：

1) 根据式（25）和式（26）更新权值。

2) 判断：2 次权值的差小于Threshold 或大于最大迭代次数MaxNum 后结束循环。

W∈Cn×(K+1)m

步骤 4 输出： 。

4 仿真分析

为了验证本文方法的有效性，仿真了3 种卷积线性混合情况的分离实验，以及本文方法与基于线性混合模型方法的解混对比实验，3 种卷积线性混合情况分别为单个复线性调频信号与复高斯干扰信号混合、多个复线性调频信号与复高斯信号混合、实测雷达脉冲回波数据与复高斯信号混合，两路信号的卷积线性混合过程由2 阶FIR 滤波器实现，滤波器系数为随机产生的复向量。源信号的自相关曲线与分离后信号和源信号的互相关曲线的重叠程度表示分离后信号是否很好地保留了原有的自相关特性，重叠程度高，代表分离后信号很好地保留了原有信号的自相关特性。通过分离后信号与源信号的相关性评估复非高斯信源提取质量的好坏，得到的相关系数越趋近于1，相关性越强，复非高斯信源的提取质量越好，反之则越差，相关系数为0 则代表提取出的信号与源信号不相关。为了尽可能避免偶然性，以下实验中得到的相关系数均为500 次蒙特卡罗实验之后的结果，实验样本点数为5 000 个。其中相关系数定义如下：

1） 瞬时和卷积线性混合模型对比实验

为了说明本文方法针对卷积线性混合模型的解混有效性，与未考虑时间延迟的解混算法进行了对比实验。图2 为信干比为-30 dB 时的卷积线性混合信号及2 个源信号的实部。可以看出，线性调频信号已经完全被淹没在高斯干扰信号中。图3 分别表示使用本文方法对卷积线性混合信源解混之后的信号及模型失配时分离卷积线性混合信号的情况，图4 为瞬时和卷积线性混合模型分离相关性对比。可以看出，没有考虑时间延迟的解混算法得到的分离信号不仅丢失了原有的自相关特性，而且与源信号的相关性很低，通过实验得到使用本文方法提取的信号与源信号的相关系数为0.998 8，模型失配时的相关系数为0.040 8，说明本文方法的有效性及明显的分离优势。

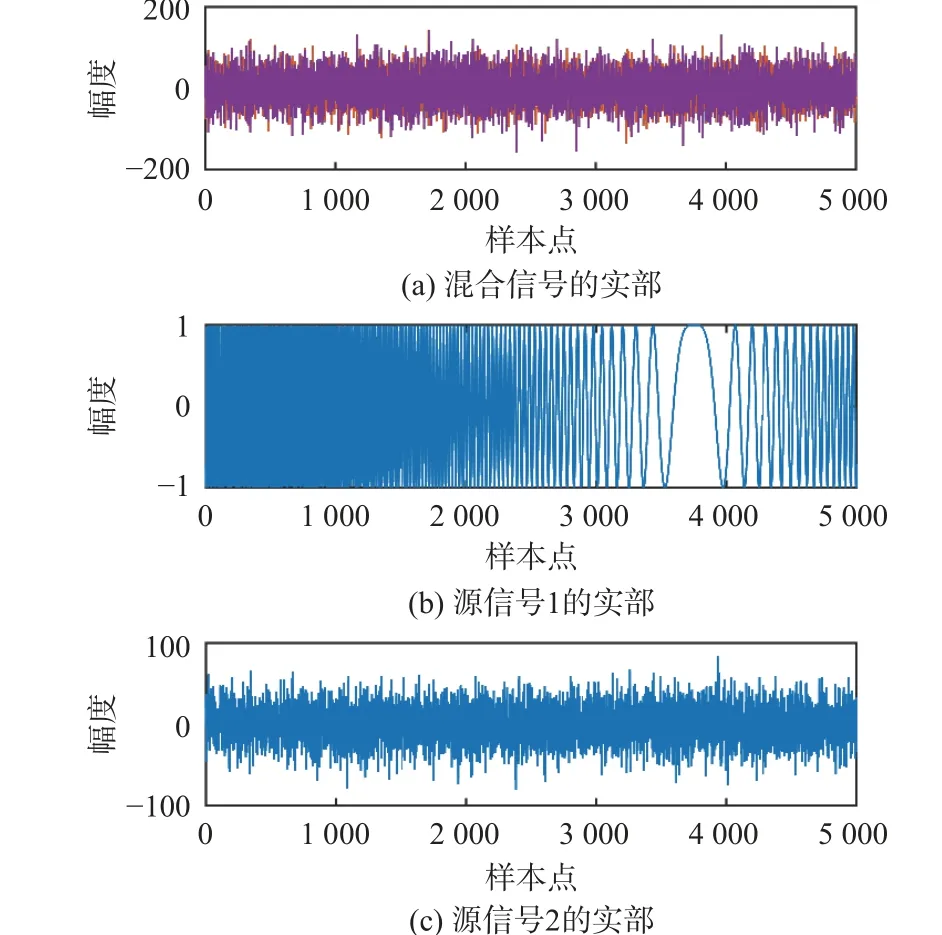
图2 单个线性调频信号与高斯干扰信号混合Fig. 2 Mixture of single linear frequency modulation signal and Gaussian interference signal

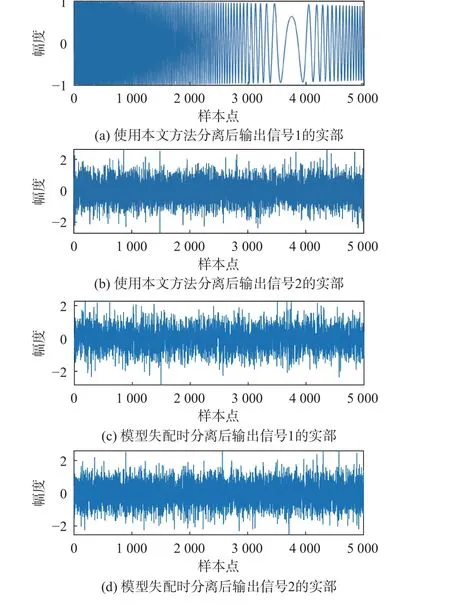
图3 瞬时和卷积线性混合模型分离效果对比Fig. 3 Comparison of separation effect between instantaneous and convolution linear mixture models

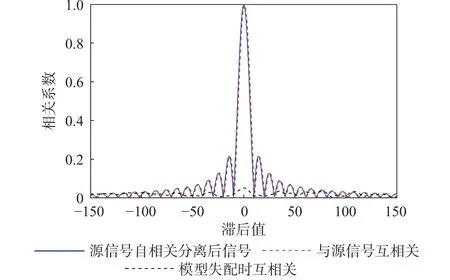
图4 瞬时和卷积线性混合模型分离相关性对比Fig. 4 Comparison of separation correlation between instantaneous and convolution linear mixture models

2） 多个复线性调频信号与复高斯干扰信号混合

为了验证本文方法也可以对多个非高斯混合信号进行有效提取，将2 个复线性调频信号与复高斯干扰信号卷积混合，在信干比为-30 dB 下，也取得了不错的分离效果。如图1 所示，在卷积线性混合模型下，将2 个复线性调频信号看作一路独立的源信号与复高斯干扰信号卷积得到两路观测信号。图5（a）～（c）为信干比为-30 dB 时的卷积线性混合信号及2 个源信号的实部。可以看出，线性调频信号已经完全淹没在高斯干扰信号中，通过本文方法解混，发现该方法可以将2 个复线性调频信号的混合形式率先分离出来。图5（d）、（e）为分离后的两路输出信号的实部显示。由于盲源分离算法具有相位模糊，得到的输出信号与源信号相比具有一定的相位差。图5（f）中，2 条曲线重叠程度较高，表明分离后的复多线性调频信号很好地保留了原有的自相关特性，并且与分离之前的复多线性调频信号具有强相关性，图中正负1 000 处2 个凸起分别为分离前后2 个复线性调频信号的互相关结果，分离后单个复线性调频信号与分离前单个复线性调频信号的互相关结果变化一致，说明将多个复线性调频信号看做一个独立源进行盲信号提取并不破坏单个复线性调频信号的相关性，通过实验得到提取的信号与源信号的相关系数为0.970 3。

图5 多线性调频信号盲源提取Fig. 5 Blind source extraction of multiple linear frequency modulation signals

3） 半实测半仿真实验

通过对实测数据的处理验证本文方法的有效性，所选用的实测数据来自某型S 波段的线性调频信号的外辐射源雷达系统接收数据,该系统工作于脉冲体制，试验模式。图6（a）为实测的单通道雷达脉冲回波数据经脉冲压缩之后的结果。图6（b）为实测雷达脉冲回波数据与一路复高斯干扰信号经过2 阶FIR 滤波器卷积线性混合之后再经脉冲压缩的结果，每个滤波器的系数是随机产生的一组复向量，信干比为-15 dB，可以看出，其中一个目标已经完全被高斯干扰信号淹没无法辨别。图6（c）为使用本文方法对该混合信号进行复非高斯信源提取之后再脉冲压缩得到的结果，可以看出，即使在被高斯干扰信号完全淹没的极端情况下，卷积线性混合模型下的复非高斯信源提取方法对于实测雷达脉冲回波数据的提取仍然有效。

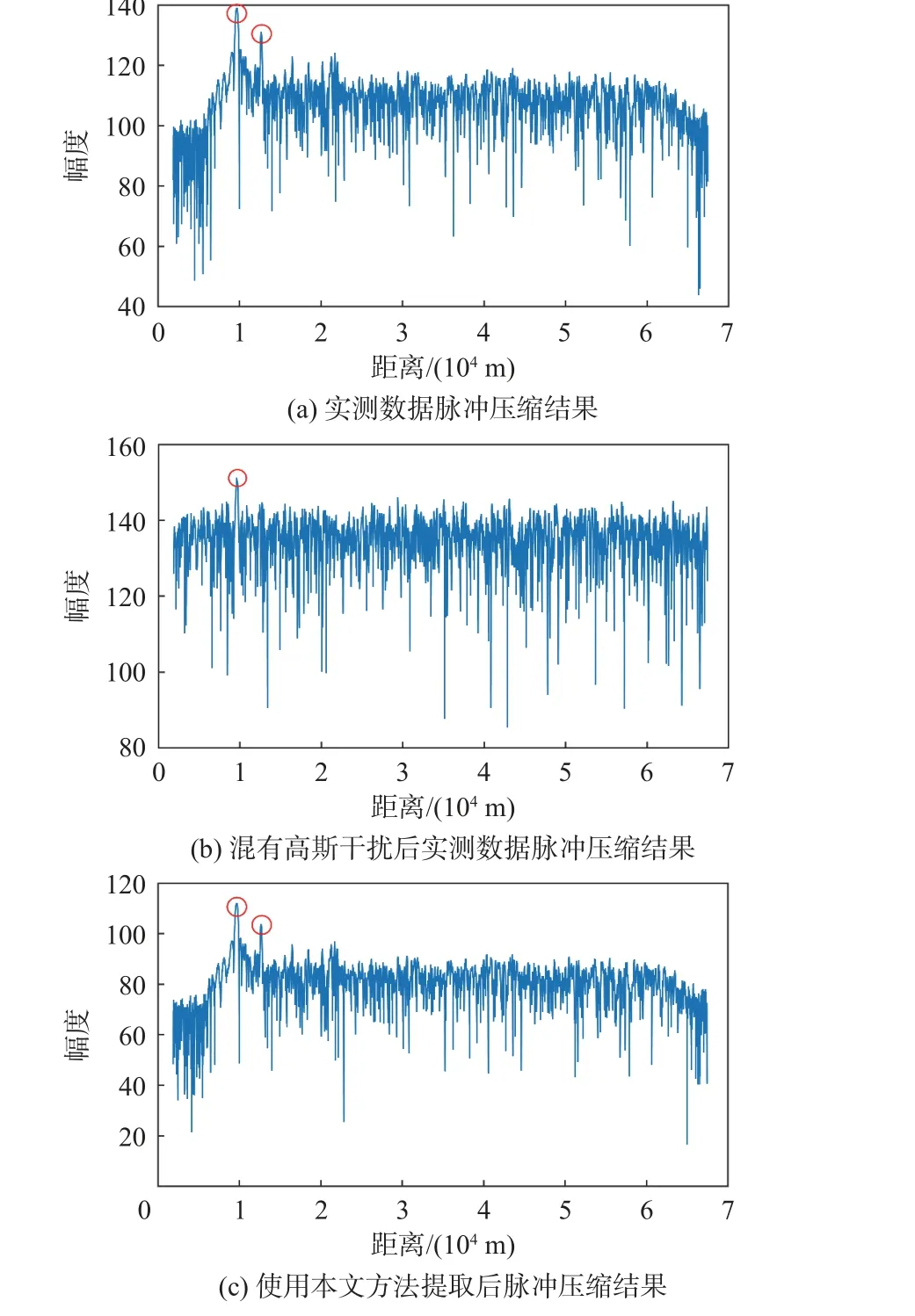
图6 雷达脉冲回波数据盲源提取Fig. 6 Blind source extraction of radar pulse echo data

5 结 论

针对雷达信号在传播过程中具有多径现象的情况，同时为了能够对复值微弱信号进行快速、有效提取，本文提出了一种基于卷积线性混合模型的复非高斯信源提取方法，主要结论如下：

1) 对基于瞬时线性混合模型的盲源分离算法进行改进，用混合FIR 滤波器矩阵代替原有的瞬时线性混合模型来描述雷达信号中的多径问题。

2) 对复数FastICA 算法中观测向量和权值向量的构造方式进行重建, 既节约了接收通道数量，又在一定程度上降低了盲源分离过程的复杂度，与没有考虑多径问题的盲源分离算法相比具有明显的分离优势。

3) 利用复数FastICA 算法对复非高斯信源的天然提取优势，实现了对混合信源中复非高斯信号的提取或对原混合信号去噪的目的。

4) 通过仿真分析证明，该方法能够对混合在强高斯信号中的复值微弱信号进行快速、有效提取。

本文方法为雷达信号处理领域中强高斯干扰背景下的微弱信号提取提供了新方法。但是在实际应用环境中，面临的情况将变得复杂，后续将针对混合多非高斯信源情况下的特定信号提取开展研究。