电机模型中牵连运动及其动生电动势的数理表达*

钟再敏， 王业勤

(同济大学 汽车学院，上海 201804)

0 引 言

法拉第电磁感应定律是电机学的基本物理定律之一。基本表述是，当穿过闭合回路所围面积的磁通量发生变化时，不论这种变化是什么原因引起的，回路中均会产生感应电动势，感应电动势的大小与通过该回路的磁通量随时间的变化率成正比；感应电动势的方向可以通过楞次定律确定[1-2]。法拉第电磁感应定律是建立交流电机定、转子绕组电压方程的基本依据。特别地，电机的分析过程中还会通过引入不同的运动坐标系来简化电压方程及方便控制算法实现。

以永磁同步电机(PMSM)定子电压方程推导为例，运动坐标系下定子电压方程的推导一般分两步[3]。

(1) 在“定子固结坐标系”中运用法拉第电磁感应定律建立电压平衡式：

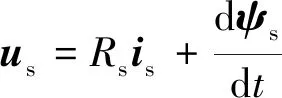
(1)

式中：us为定子电压矢量；Rs为定子绕组电阻；is为定子电流矢量；ψs为定子磁链矢量。

ψs包含永磁互感磁链ψf和定子自感磁链Lsis，即：

ψs=Lsis+ψf

(2)

式中：Ls为定子绕组自感。

在本文中，省略以定子固结(静止)坐标系为参考系的矢量上角标。以其他(非静止)坐标系为参考系的矢量，采用上角标明确标明其参考系。

定子磁链是一个旋转的空间矢量，其极坐标形式为

ψs=ψsejθs=ψsejρ0ejθr

(3)

式中：θs为定子磁链在定子固结坐标系中的相位角，θs=θr+ρ0,θr为转子相位角；ρ0为定子磁链相对转子轴线的相位角。

根据求导法则，磁链的微分推导如下：

(4)

式中：ωr为转子角速度，ωr=dθr/dt。

式(4)对应的空间矢量图如图1所示。

基于此，在定子坐标系下列出定子电压方程:

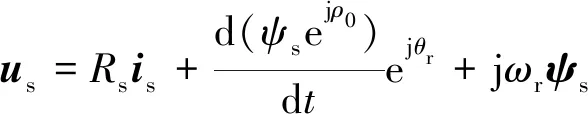
(5)

如果以“转子固结坐标系”为参考系，式(4)中第一项对应转子运动参考系下定子磁链的相对运动；第二项对应参考系引起的牵连运动，二者合成为磁链的绝对运动。电压方程式(5)表明，定子供电电压分别消耗在电阻压降、转子旋转引起的动生电动势(牵连运动)和牵引定子磁链在转子坐标系内的变化(相对运动)。

(2) 显然，在定子坐标系下，上述各空间矢量均是空间上不断旋转的交变量。因此，引入转子(磁场)同步运动dq坐标系，即对电压方程进行频率变换。

其推导过程如下，考虑矢量变换关系：

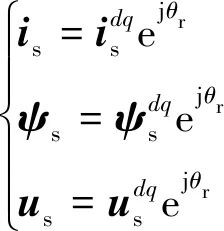
(6)

式中：上角标“dq”为以转子同步dq坐标系作为参考系。

式(6)代入式(5)则有：

(7)

化简式(7)得dq坐标系下的空间矢量方程：

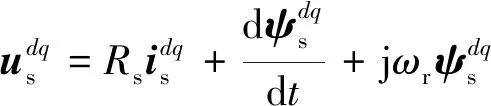
(8)

上述基于“矢量变换”的电压方程两步推导过程严谨，很多电机学教材均是基于这个逻辑建立运动参考系下的空间矢量方程。类似地，式(8)也可以通过“坐标变换”推导。但是上述推导过程较强依赖数学运算，物理意义不明确，不便于理解和记忆。

1 “法拉第参考系”与“非法拉第参考系”的概念

牛顿力学中区分“惯性参考系”和“非惯性参考系”。通常把适用牛顿运动定律的参考系叫做惯性参考系，简称惯性系；非惯性参考系是相对惯性参考系做加速运动的参考系，简称非惯性系[4-5]。一般地，在忽略地球自转和公转角速度的情况下(这两者均很小)，惯性系可以简单选成是相对地面静止的或者做匀速直线运动的参考系，而非惯性系则是相对地面做加速或者减速运动的参考系。

以质点直线运动为例，为分析方便，非惯性系中须引入附加“惯性力”：

fa=-ma

(9)

式中：a为非惯性系相对惯性系的加速度；m为质点的质量。

引入惯性力后，形式上，在非惯性参考系中也可以完全按照牛顿定律进行物体的力学分析了。

参照牛顿力学的惯性参考系概念，本文对电机分析里面的坐标系加以区分：(数学上)符合法拉第电磁感应定律的坐标系称为法拉第参考系，简称“法拉第系”；否则称为非法拉第参考系，简称“非法拉第系”。一般地，与线圈固结的坐标系为法拉第系，否则为非法拉第系。注意，对于电机中存在相对运动的不同绕组而言，其法拉第参考系的定义是不同的。

与非惯性系中引入惯性力的分析方法类似，在非法拉第参考系中，须补充由参考系牵连运动引起的动生电动势，然后才能按照法拉第电磁感应定律分析，在此称之为“牵连运动电动势”，简称“牵连电动势”。对于任意DQ旋转参考系，牵连电动势的表达式为

2.2.3措施组成主要包括沟头跌水、沟底植物水道、沟坡植物防护和沟岸防护林等多种措施。在实施过程中，应优先布设植物措施，不能直接布设但通过工程修整后可用植物措施的也优先选用；因地制宜选取适宜的植物种类及苗木；对于植物措施难以有效防控的沟段，辅以工程措施。

em=-jωDψD

(10)

式中：ωD为非法拉第系相对“线圈固结坐标系”的旋转角速度；ψD为磁链在对应非法拉第系下的矢量表示；上角标“D”为该物理量以任意DQ运动参考系作为参考系。

列写电压方程时，牵连电动势正方向定义与线圈供电电压一致，写在等式的左边。

牵连电动势的推导与前面分析过程基本类似。考虑DQ运动参考系，其旋转角速度为ωD。记定子磁链为

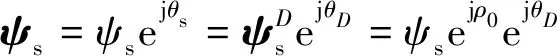
(11)

参照式(6)～式(8)的矢量变换过程，可以得到DQ坐标系下的电压方程为

(12)

移项后可得:

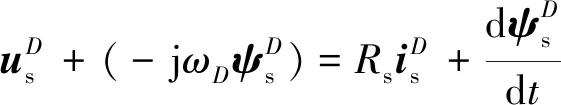
(13)

图2 任意旋转DQ参考系引入的牵连电动势

引入牵连电动势之后，形式上就可以直接在非法拉第系下建立电压方程，而无须由法拉第系经矢量或坐标变换得到。其基本步骤是在电压方程建立之前，先判断所分析的参考系是否属于法拉第系。若参考系为法拉第系，直接列写电压方程；若为非法拉第系，则须先在方程左边补充牵连电动势项，之后再列写电压方程。

2 基于附加牵连电动势的交流电机电压方程推导

2.1 PMSM电压方程

仍以PMSM定子电压方程推导为例。考虑到磁场同步dq坐标系为非法拉第系，若想直接在转子同步坐标系下列写电压方程，须补充牵连电动势项，其几何表示如图3所示。

图3 PMSM dq坐标系下的牵连电动势

考虑了牵连电动势之后，在运动坐标系(非法拉第系)下可以直接列写定子电压平衡方程为

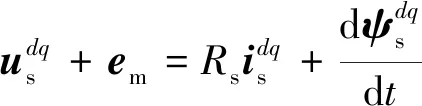
(14)

em表达式为

(15)

式(15)代入式(14)得到:

(16)

显然式(16)与式(8)相同。最终得到的电压方程对应的空间矢量几何描述如图4所示。

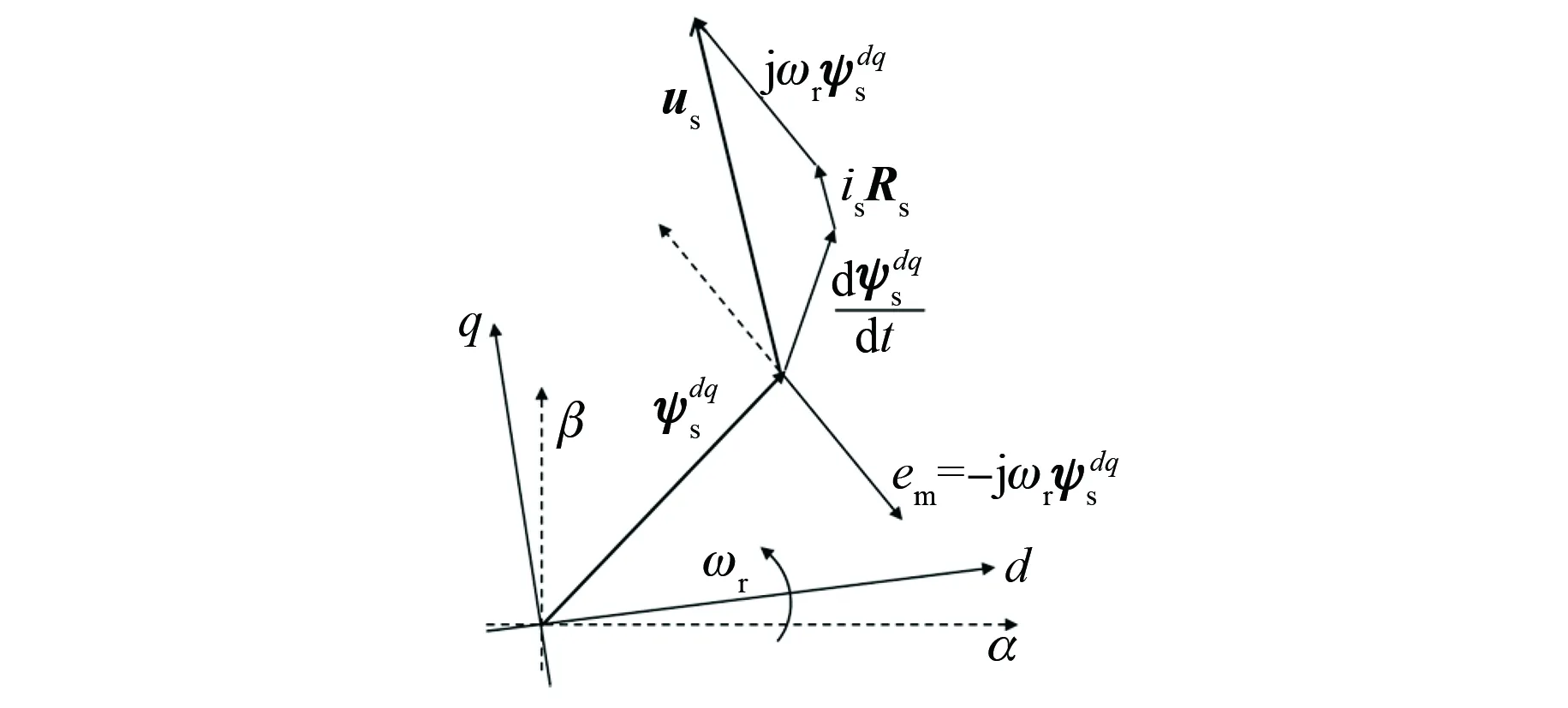
图4 PMSM dq参考系下的电压矢量平衡

图4电压矢量图清楚地表明了，在非法拉第系下，定子电压矢量对电流和磁链的调节要首先扣除参考系牵连运动引起的牵连电动势。

2.2 感应电机电压方程

与同步电机相比，感应电机分析相关的运动参考系要复杂很多。常见的参考系包括定子固结坐标系、转子固结坐标系、磁场同步坐标系等，详见图5。

图5 感应电机不同参考系及其旋转速度[2]

对于定子绕组而言，定子固结ABC坐标系与绕组固结，属于法拉第参考系，可直接列写静止坐标系下定子电压矢量方程：

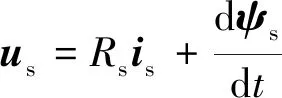
(17)

对于转子绕组而言，转子固结abc坐标系属于法拉第参考系，可得相应转子电压矢量方程为

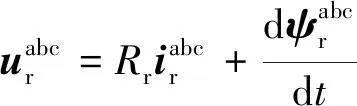
(18)

式中:上角标“abc”为转子abc坐标系中矢量的上标角；Rr为每相绕组电阻。

定子固结ABC坐标系对于转子来说是非法拉第参考系，相对旋转角速度是-ωr。因此，以定子固结ABC坐标系表示的转子电压方程，须附加牵连电动势：

em=-j(-ωr)ψr=jωrψr

(19)

此时，转子电压方程为

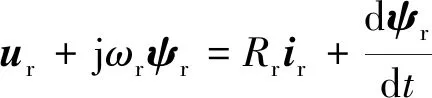
(20)

定子固结ABC坐标系下转子绕组附加牵连电动势几何解释如图6所示。

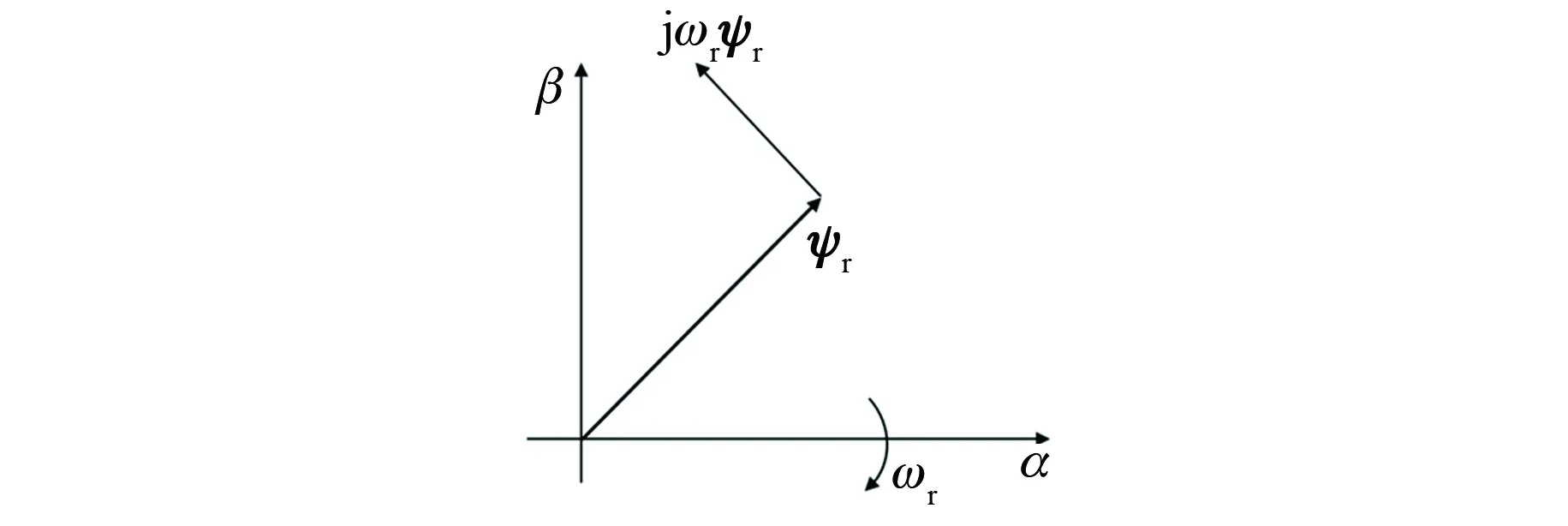
图6 定子固结ABC坐标系下转子绕组附加牵连电动势

在线圈固结坐标系下，感应电机各矢量是旋转的交变量，不易分析和控制。

为此，考虑在磁场同步旋转的DQ坐标系下建立电压矢量方程，而DQ坐标系对于定、转子绕组而言均是非法拉第系。

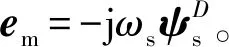
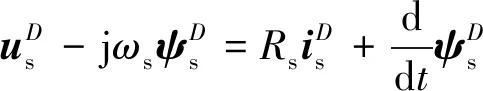
(21)

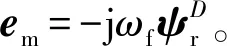
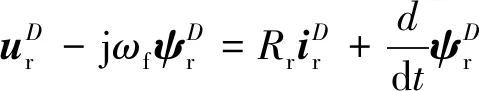
(22)

相对于基于旋转变换的推导方式，基于非法拉第参考系和附加牵连电动势，可直接在运动坐标系下列出电机电压方程，物理意义清晰，便于理解和工程应用。DQ坐标系也可以选为任意非磁场同步坐标系，推导过程基本一致。

3 结 语

在牛顿力学体系中，惯性参考系和惯性力概念的引入，极大地方便了动力学方程的推导，特定情况下，更可以将动力学问题转化为静力学问题，是一个重要的分析手段。

本文介绍的方法，创新地引入法拉第参考系和对应的牵连运动电动势的概念，其有益效果是赋予牵连运动引起的动生电动势明确的物理含义，进而可以直接在任意运动坐标系中建立绕组的电压平衡方程。

上述概念方法尽管只是一类数学推导的物理解释，但该方法的数理基础是矢量微分在运动参考系下的分解，一定程度上可以推广到其他需要引入(平动或者更复杂形式的相对运动)中间参考坐标系的类似电磁系统分析计算，具有普遍适用性。