远端电网故障下双馈式变速抽水蓄能机组平衡点存在性研究
2023-02-03孙士涛
雷 雨, 孙士涛, 宋 鹏, 张 杰
(华北电力科学研究院有限责任公司,北京 100045)
0 引 言
随着我国电力系统新能源接入占比持续增加,系统功率波动、调峰调频等问题凸显,抽水蓄能机组具有发电、水泵双运行模式,可完成功率的双向调节。抽水蓄能机组是解决系统功率平衡、调峰调频等问题的主要手段[1-3]。变速抽水蓄能机组调节范围宽、功率响应快、运行灵活,其中采用部分功率变流器的双馈式变速抽水蓄能机组(DF-VSPSU),近年来得到了广泛关注。
为确保电力系统的安全运行,低电压穿越已成为并网装备的基本并网要求:在电压跌落期间注入无功电流以支撑电网电压[4-5],也可以利用功率裕量注入有功电流,以防止系统出现有功缺额而影响系统频率稳定。低电压穿越期间,双馈电机稳定性主要可分为小扰动稳定、大扰动稳定。在小扰动方面,文献[6-7]指出锁相环(PLL)与双馈电机转子电流环间的相互作用导致中低频段阻尼不足是引起小扰动振荡失稳问题的关键原因。在此基础上,文献[8-9]研究了低电压穿越期间双馈电机有功电流受控目标对其运行稳定性的制约关系。文献[10-11]分析了不同故障位置对新能源发电并网系统稳定性的影响。这些研究[6-11]的本质要求是在稳定工作点处线性化模型状态矩阵或传递函数的特征值均位于左半平面,可借助特定平衡点处的线性化系统模型进行分析。在大扰动方面分析,文献[12-13]指出由于电网阻抗的存在会使新能源并网装备的稳定运行范围明显缩小,同时不合适的有功电流、无功电流受控目标会导致机组出现失稳现象。文献[14-15]建立了描述PLL动态的二阶微分方程,并借鉴相图分析方法识别并网稳定性。这些研究均基于非线性大信号模型,重点关注故障前后两个平衡点间的过渡过程。综上,前述研究关注机组在平衡点处的稳定性以及能否顺利过渡到新的平衡点,然而电网故障后机组有功、无功出力对系统平衡点存在性影响还有待研究,这也是制约机组低电压穿越运行成功与否的必要前提。
因此,本文以单DF-VSPSU无穷大系统为例,建立了DF-VSPSU机侧特性和网侧特性方程,刻画了不同接入环境下DF-VSPSU运行可行域,并分别从远端电压跌落深度、电网短路比、电网阻抗角、机组无功支撑系数4个因素分析对其运行平衡点存在性的影响。最后,通过MATLAB/Simulink仿真验证了理论分析。
1 低电压穿越策略
图1给出了DF-VSPSU接入电网阻抗不可忽略的单机无穷大结构图。其中,DF-VSPSU电流正方向指向电网,下标abc、dq分别表示电气量在三相静止abc坐标系、两相同步旋转dq坐标系下的形式,下标s、r分别表示双馈发电电动机定、转子绕组,E、Us、Is、Ir分别表示远端电压矢量、机端电压矢量、定子电流矢量、转子电流矢量;Zg∠θg=Rg+jXg为电网等效阻抗,Rg、Xg分别为电网等效电阻、电抗,Zg、δg分别为电网阻抗幅值和阻抗角;θr、ωr、ωpll分别表示双馈发电电动机转子位置角、角速度和PLL输出电网角频率;ωs=ωpll-ωr为滑差角速度;Ps、Qs、Psref、Qsref分别为双馈发电电动机定子有功、无功功率及其目标参考值。由于DF-VSPSU转差率一般在±4%~±7%之间,则其网侧变流器传输功率较小,而机侧变流器对功率传输起主导作用。为便于分析,忽略DF-VSPSU网侧变流器动态,后续分析重点关注DF-VSPSU机侧变流器与故障电网间的相互关系。
在低电压穿越期间,DF-VSPSU机侧变流器控制系统由常规定功率控制切换为定电流控制,通过对机端有功、无功电流进行调控,满足低电压穿越期间的技术标准要求。因此,远端电网故障期间,双馈发电电动机有功、无功电流受控目标可表示为
(1)
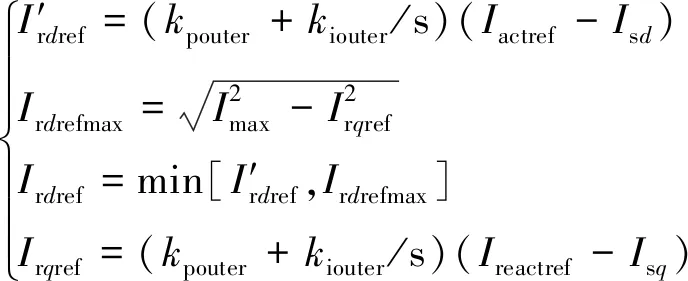
(2)
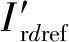
DF-VSPSU机组在检测到电网故障后,将进入定电流控制的低电压穿越控制模式,其中:无功电流受控目标由预设定的电压-无功电流曲线确定,有功电流受控目标由提供无功支撑后的变流器功率裕量决定。在低电压穿越期间,双馈发电电动机通过注入有功、无功电流,支撑电网电压,然而有功、无功电流注入过多后,可能会导致双馈发电电动机运行平衡点不存在,需进一步的研究。
2 数学模型
由于本文重点关注远端电网故障下DF-VSPSU机组运行平衡点存在性,则可采用准稳态模型,即忽略双馈发电电动机定子磁链动态,则电压、磁链方程可写为
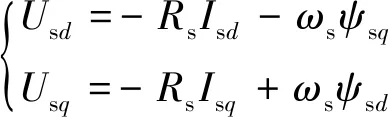
(3)
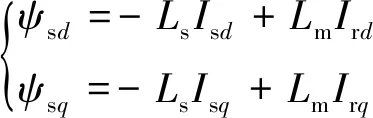
(4)
式中:Lm、Ls、Rs为励磁电感和定子电感、电阻;Usd、Usq为定子电压d轴、q轴分量;Ird、Irq为转子电流d轴、q轴分量;ψsd、ψsq为定子磁链d轴、q轴分量。
通常,对于大容量电机而言,其定子电阻一般较小而可忽略,则双馈发电电动机转子d、q轴电流可表示为
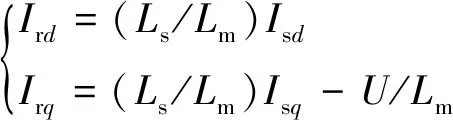
(5)
在准稳态模型中,可认为双馈发电电动机定、转子电流能够完成对受控目标的跟踪。在电网故障后,双馈发电电动机在提供无功电流的同时,充分利用其机侧变流器功率裕量输出有功电流,以支撑电网电压,此时双馈发电电动机转子电流达到最大值,则有:
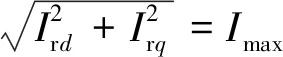
(6)
因此,根据式(2)、式(6),在远端电网故障下,双馈发电电动机转子电流可表示为
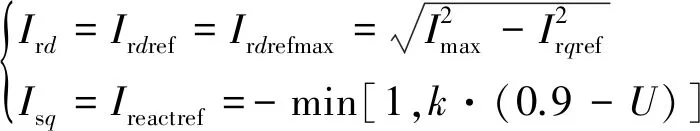
(7)
将式(5)代入式(7)后,可得双馈发电电动机有功电流,具体为
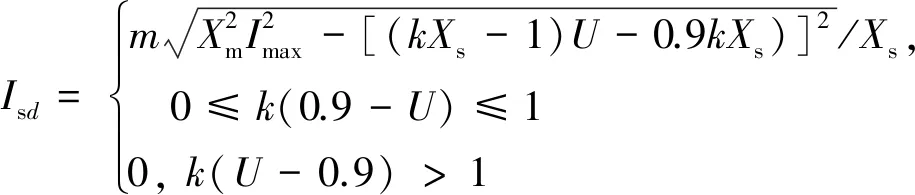
(8)
式中:Xm、Xs分别为励磁电抗、定子电抗;m为双馈式发电电动机运行状态参数,m=-1为水泵状态,m=1为发电状态。
同时,双馈发电电动机q轴电流,即无功电流,可表示为
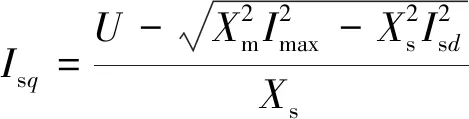
(9)
从双馈发电电动机机端向远端电网看,机端电压与远端电网电压关系可写为
E2=(U+IsqZ1sinθ1-IsdZ1cosθ1)2+
(IsdZ1sinθ1+IsqZ1cosθ1)2
(10)
可知,在远端电网故障下,DF-VSPSU机组输出有功、无功电流与电网阻抗、远端电网电压有关,同时也会受到变流器容量限制。为便于后文分析,将式(9)给出的DF-VSPSU机组定子电流特性称为机侧特性方程,并且将式(10)给出的远端电网特性称为网侧特性方程。这也就是说,在远端电网故障下,DF-VSPSU运行边界是由网侧特性方程和机侧特性方程共同决定。
3 边界条件
根据式(9),双馈发电电动机机侧特性方程,则有:
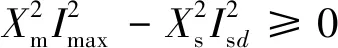
(11)
则定子电流边界条件可写为
-XmImax/Xs≤Isd≤XmImax/Xs
(12)
可知,机侧特性方程主要限制因素为机侧变流器最大允许电流,而与水泵、发电状态无关,则双馈发电电动机机侧特性方程决定的有功电流边界呈现对称特性。
根据式(10),在机端电压d轴定向的两相同步旋转坐标系中,远端电网电压dq轴分量可以表示为
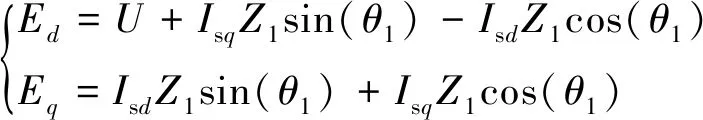
(13)
式中:Ed、Eq分别为远端电网电压的d轴、q轴分量幅值。
则双馈发电电动机机端电压可表示为
IsdZ1cos(θ1)-IsqZ1sin(θ1)
(14)
式中:E为远端电网电压。
在实际运行中,为获取式(13)所示的DF-VSPSU机端电压,则有如下要求:
-E≤IsdZ1sin(θ1)+IsqZ1cos(θ1)≤E
(15)
图2给出了远端电压跌落下DF-VSPSU运行边界,其中机侧边界由式(12)确定,网侧边界由式(14)确定。在图2中,DF-VSPSU接入短路比(SCR)为3.0,阻抗角为80°的电网,随着远端电压跌落深度逐渐减小,DF-VSPSU运行轨迹逐渐外扩,从而形成DF-VSPSU可行域。由于电网阻抗分压的作用,使得DF-VSPSU运行轨迹向上偏移,根据式(14)可知,在发电模式下,当无功电流与有功电流幅值的比值等于阻抗角正切值时,则DF-VSPSU支撑效果最优,而当有功输出电路继续增加时,DF-VSPSU无功电压支撑能力弱化,其下降水平将超过有功电流对线损的补偿水平,导致机端电压的下降。而在水泵模式下,DF-VSPSU有功电流增加将会导致无功电压支撑能力弱化,并叠加阻抗的分压作用,导致机端电压下降。综上,当远端电网故障后,DF-VSPSU可行域于机侧上、下边界之间与网侧边界左侧,如图2所示,并呈现椭圆状,且随着远端电压跌落深度的增加而逐渐缩小。
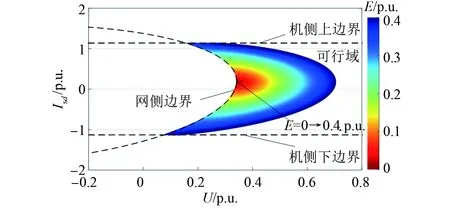
图2 DF-VSPSU运行边界
4 平衡点分析
根据前述分析,在低电压穿越期间,DF-VSPSU平衡点与远端电压跌落深度、电网SCR、电网阻抗角、无功支撑系数有关。因此,本节针对上述4种因素进行具体分析,以明晰对DF-VSPSU平衡点存在性的影响。
4.1 远端电压跌落深度
图3给出了电网SCR为3.0、阻抗角为80°时,不同远端电压跌落深度下DF-VSPSU机端电压与其有功电流的相平面图,其中:Isd>0表示输出有功电流,DF-VSPSU运行于发电状态;Isd<0表示吸收有功电流,DF-VSPSU运行于水泵状态。在故障电压下,根据式(9),DF-VSPSU无功支撑系数的增加会导致其可输出的有功电流将会降低,使得机侧特性运行轨迹逐渐向右侧偏移。在发电工况下,根据式(14),当无功电流与有功电流幅值的比值高于电网阻抗角正切值时,通过有功电流对线路压降的补偿,机端电压呈增加趋势。而随着有功电流的逐渐增加,使得无功电流与有功电流幅值的比值低于电网阻抗角正切值时,此时线路上无功电压支撑程度下降水平会超过有功电流对线损的补偿,导致机端电压下降。但在水泵工况下,有功电流的增加弱化了无功电压支撑水平,并叠加电网阻抗分压作用,使得机端电压呈现单调递减趋势。
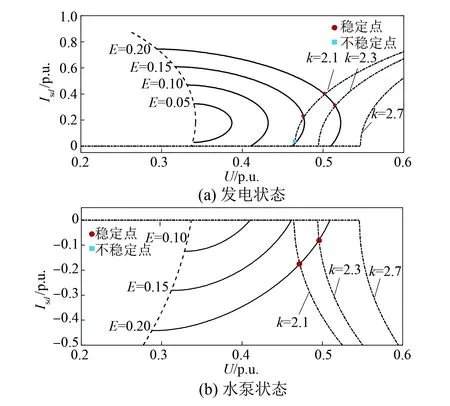
图3 不同电压跌落深度下机端电压-有功电流
从图3可见,随着无功支撑系数的增加,DF-VSPSU的机侧稳态运行轨迹与网侧稳态运行轨迹逐步由两个交点,变为一个交点,再到无交点。这里需要指出,在发电状态下,当DF-VSPSU机侧轨迹相交与网侧轨迹递减区间内时,该交点为稳定平衡点(圆点),而二者相交于网侧轨迹递增区间内时,该交点为不稳定平衡点(方块)。这主要由于当DF-VSPSU机端电压出现小扰动导致机端电压增加时,DF-VSPSU机侧轨迹的递增特性,其输出有功电流将会增加,根据式(14),DF-VSPSU机端电压会升高,而后进入网侧轨迹递减区间,在此区间内机端电压会随着有功电流的增加而递减,当二者再次相交后即为稳定平衡点。在水泵状态下,随着无功支撑系数的增加,机侧稳态运行轨迹与网侧稳态运行轨迹逐步由一个交点到没有交点。DF-VSPSU稳态运行轨迹的单调性不变,因而仅会存在一个平衡点,即为稳定平衡点。在该平衡点处,当受到小扰动而导致机端电压下降时,根据机侧轨迹可知,其输入的有功电流将会降低,并且根据式(14),机端电压会上升,进而使得输入有功电流增加,而后逐步收敛于稳定平衡点。在水泵状态下,机侧特性方程与网侧特性方程的运行轨迹的交点即为稳定平衡点。
4.2 电网SCR
图4给出了远端电压跌落为20%、阻抗角为80°时,不同电网SCR下DF-VSPSU机端电压与其有功电流的相平面图。其中,机侧稳态运行轨迹由于机组参数不变,而呈现出与图3相同的趋势;同时,根据式(14)可知,网侧稳态运行轨迹由于电网SCR降低,即电网阻抗增加,机组输出有功、无功电流对机端电压支撑效果更为明显。
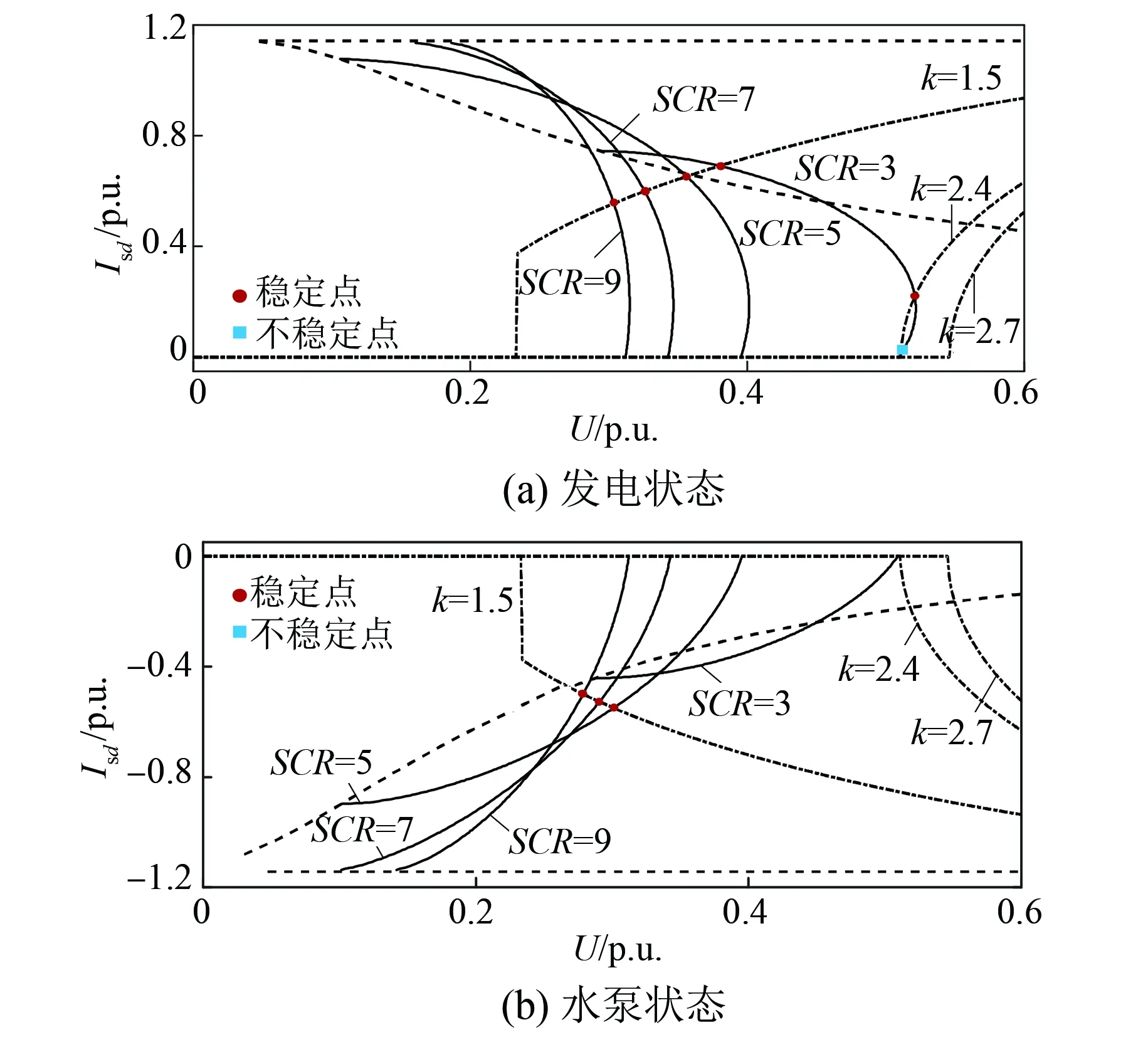
图4 不同电网SCR下机端电压-有功电流
从图4可见,在电压跌落深度相同时,机组运行轨迹先交于网侧边界,但随着电网SCR的增加,同样输出电流对电压影响逐渐降低,而达到机侧上、下边界,此时机侧变流器输出电流达到最大值。以电网SCR为3.0为例,当DF-VSPSU无功支撑系数为2.3时,DF-VSPSU机侧轨迹与网侧轨迹存在两个交点,根据前述分析可知,处于单调递减区间的圆点为稳定平衡点,而方块为不稳定平衡点。随着DF-VSPSU无功支撑系数逐渐减小,机侧轨迹与网侧轨迹交点逐渐左移,将会出现机侧轨迹与网侧稳态轨迹不存在相交的情况。当无功支撑系数为1.5时,处于水泵状态的DF-VSPSU机侧稳态运行轨迹与网侧稳态运行轨迹不存在交点,因而此种工况下不存在平衡点。
4.3 电网阻抗角
图5给出了远端电压跌落为20%、电网SCR为3.0时,DF-VSPSU在发电、水泵状态下机端电压与其有功电流的相平面图。其中,机侧稳态运行轨迹不变,而网侧稳态运行轨迹,而根据式(14)可知,由于电网阻抗角降低而其阻抗不变,DF-VSPSU的机端电压变化拐点将会升高,但其所对应的机端电压最大值不变。
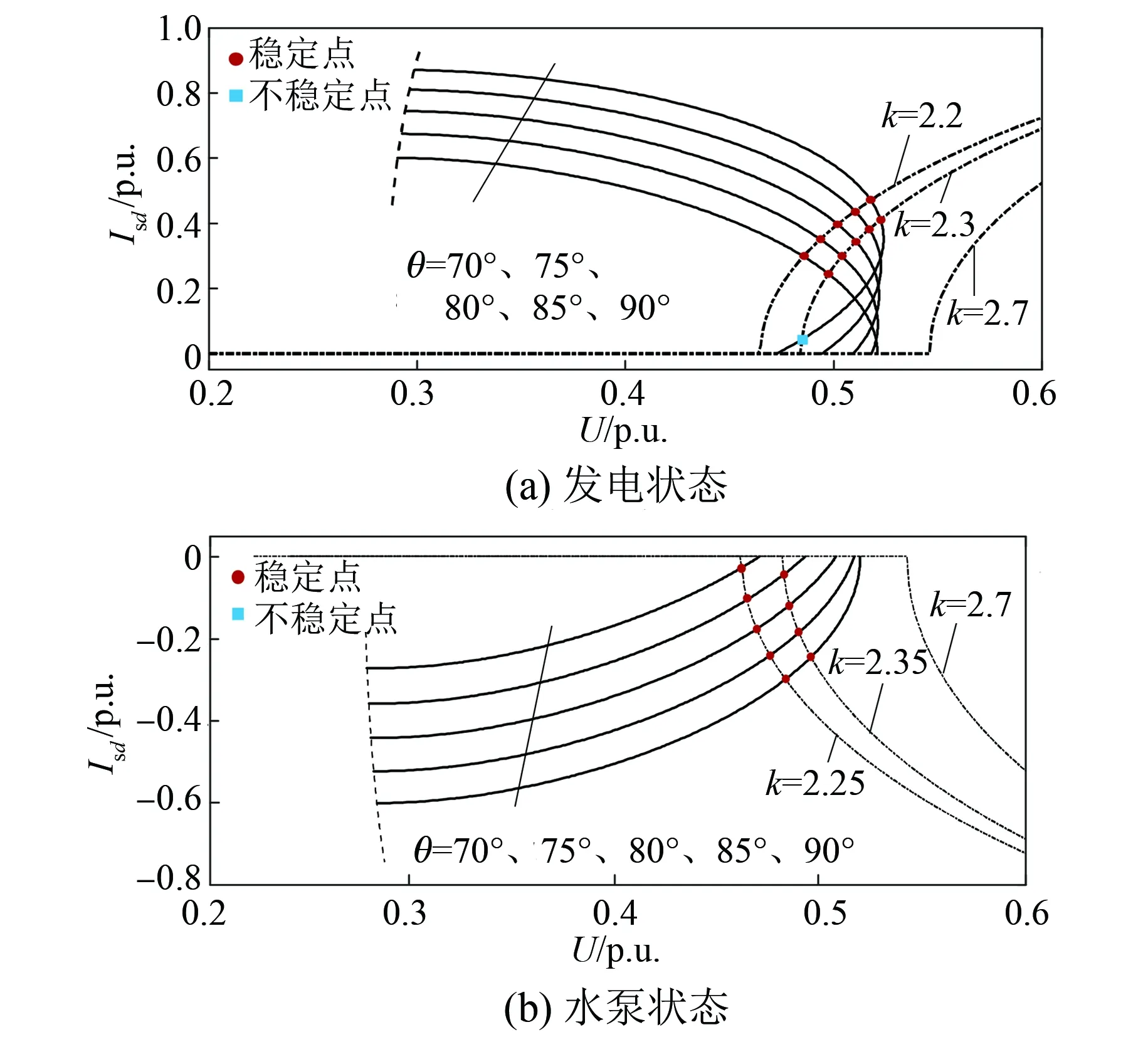
图5 不同电网阻抗角下机端电压-有功电流
从图5可见,随着无功支撑系数的增加,在发电模式下,机侧轨迹与网侧轨迹从一个交点,到两个交点,最后不存在交点。当无功支撑系数为2.3、阻抗角θ为90°时,DF-VSPSU的机侧、网侧稳态运行轨迹存在两个交点,其中处于单调递减区间的圆点为稳定平衡点,而方块为不稳定平衡点。而当无功支撑系数增加至2.7时,机侧轨迹与网侧轨迹无交点。在水泵状态下,DF-VSPSU机组的机侧轨迹与网侧轨迹最多有一个交点,即为稳定平衡点。随着无功支撑系数的增加,机侧轨迹与网侧轨迹也将出现无交点情况。
4.4 无功支撑系数
考虑电网阻抗角由线路电抗、电阻决定,而与线路长短、远端电压跌落深浅无关,则在假定电网阻抗角为80°时,图6给出了电网SCR、远端电压变化下DF-VSPSU无功支撑系数最大允许值。当DF-VSPSU无功支撑系数继续增加,则机侧稳态运行轨迹与网侧稳态运行轨迹无法相交,因而不存在平衡点。
从图6可见,DF-VSPSU无功支撑系数最大允许值随着远端电压跌落深度、电网SCR增加而减少。然而,在同样远端电压跌落与电网SCR下,发电状态下DF-VSPSU无功支撑系数要略低于水泵状态下无功支撑系数。这主要是处于发电状态的DF-VSPSU输出有功电流可以起到机端电压支撑作用,而处于水泵状态下机组消耗的无功电流所产生的电网阻抗分压,会使得机组的机端电压低于发电工况下机组的机端电压。
5 仿真分析
为验证对远端电网故障下DF-VSPSU机组平衡点分析的有效性,利用MATLAB软件,建立如图1所示的DF-VSPSU接入远端电网仿真模型,其中双馈发电电动机参数如表1所示,krp、kri分别为转子电流内环的比例、积分系数,ksp、ksi分别为低穿控制外环内环的比例、积分系数。
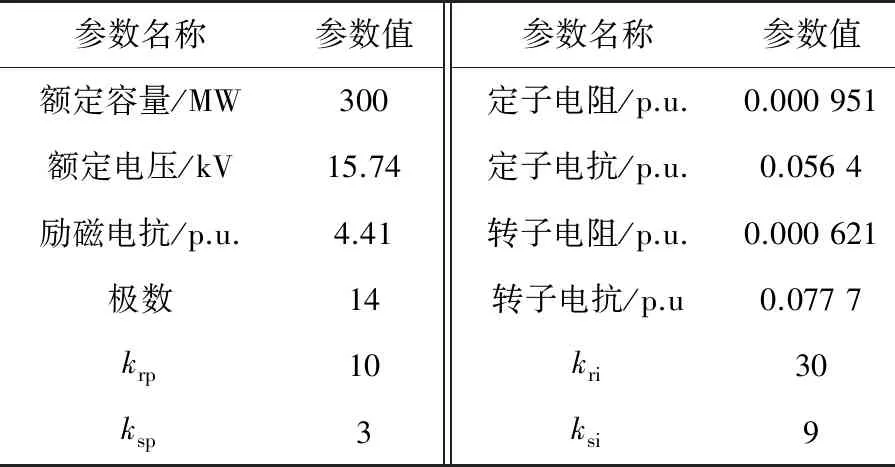
表1 双馈发电电动机参数
图7给出了远端电压跌落下DF-VSPSU发电工况仿真结果,其中:远端电压跌至0.2 p.u.、电网SCR为3.0、电网阻抗角为80°。DF-VSPSU无功支撑系统初始设定为k=1.8,在0.5 s时刻无功支撑系数阶跃为k=2.5。可见,在0~0.5 s期间,根据式(1),DF-VSPSU输出有功、无功电流目标参考值分别为0.57 p.u.、0.82 p.u.,而根据仿真结果可知,DF-VSPSU有功、无功电流分别为0.56 p.u.、0.83 p.u.,定子电流达到最大允许值1.0 p.u.,此时机端电压达到0.45 p.u.。根据图6(a),在此电网条件下,DF-VSPSU无功支撑系数最大为2.42,小于设定值,系统不存在平衡工作点。在0.5 s时,DF-VSPSU无功支撑系统变为k=2.5,其输出的功率、电流存在明显波动,机组出现振荡失稳现象,也说明系统不存在平衡点。
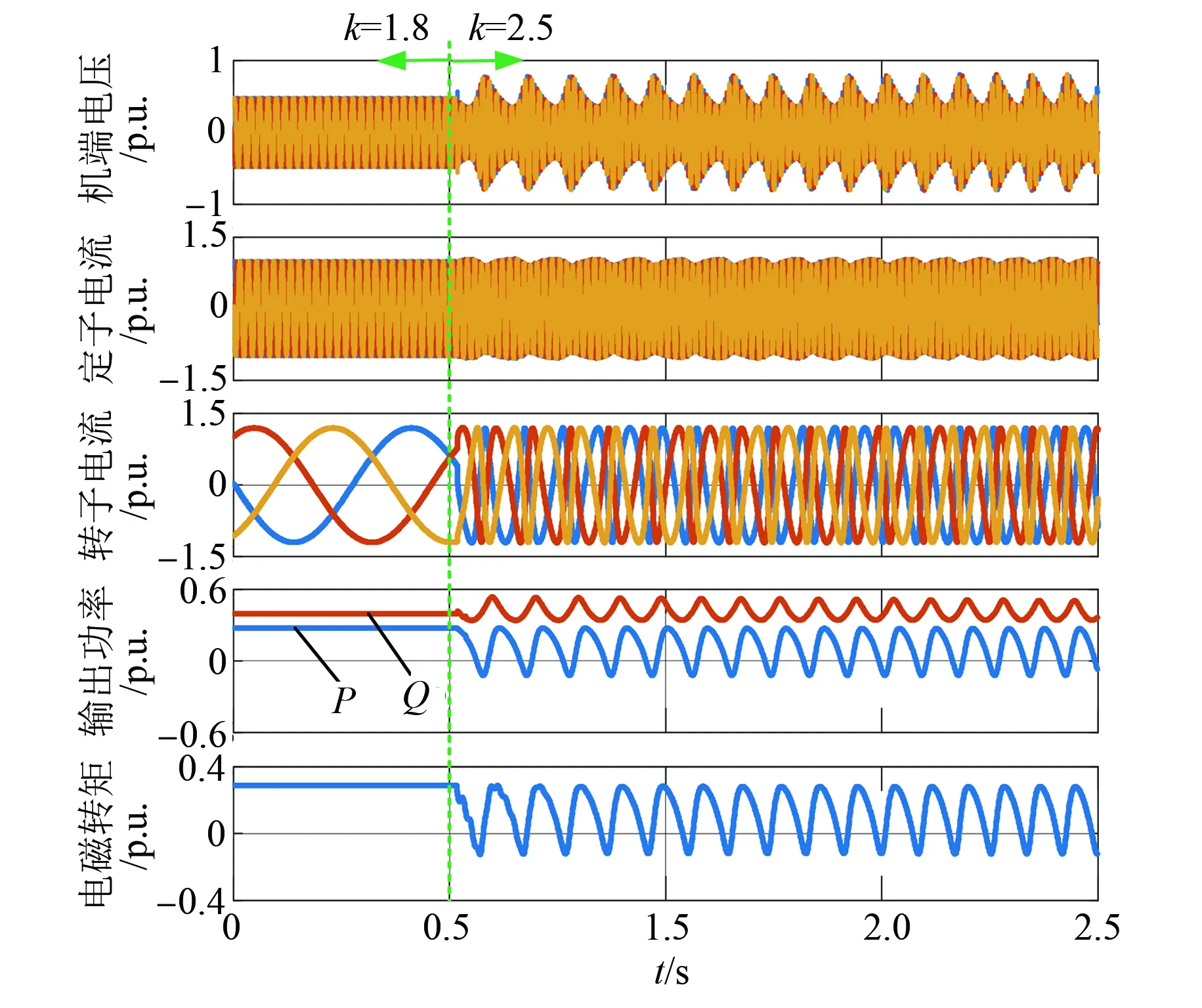
图7 远端电压跌落下DF-VSPSU仿真结果(发电)
图8给出了远端电压跌落下DF-VSPSU水泵工况仿真结果,其电网条件与图7相同。DF-VSPSU无功支撑系统初始设定为k=1.8,在0.5 s时刻无功支撑系数阶跃为k=2.5。可见,在0~0.5 s期间,根据式(1),DF-VSPSU输出有功、无功电流受控目标分别为0.36 p.u.、0.94 p.u.,而根据仿真结果可知,DF-VSPSU有功、无功电流分别为0.57 p.u.、0.93 p.u.,此时机组机端电压仅为0.35 p.u.。这主要是由于水泵工况下,DF-VSPSU输入的有功电流导致线路电阻分压,使得机端电压降低。根据图6(b),在此电网条件下,DF-VSPSU无功支撑系数最大为2.40,小于设定值,系统不存在平衡工作点。图8所示仿真结果在0.5 s后出现功率、转矩振荡失稳现象,验证了理论分析的合理性。
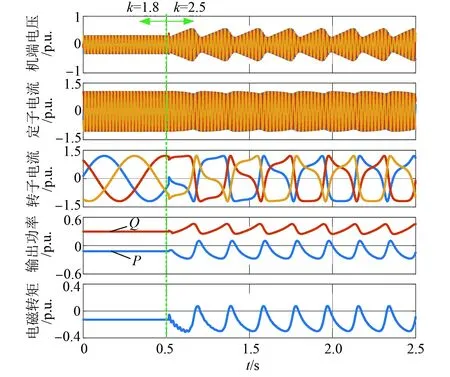
图8 远端电压跌落下DF-VSPSU仿真结果(水泵)
6 结 语
本文通过建立DF-VSPSU机侧特性和网侧特性方程,刻画了DF-VSPSU运行可行域,并探究了远端电压跌落深度、电网SCR、电网阻抗角、无功支撑系数对DF-VSPSU平衡点存在性的影响。同时,结合DF-VSPSU的机侧和网侧特性方程,本文给出了DF-VSPSU无功支撑系数最大允许值。当无功支撑系数超过最大允许值时,DF-VSPSU不存在平衡点,而出现振荡失稳情况。最后,通过仿真验证了本文理论分析的合理性。
