增材制造BCCZ点阵夹芯梁结构的自由振动分析

张武昆，谭永华，高玉闪，王 珺，赵 剑,耿小亮

(1.西安航天动力研究所，西安 710100；2.西安航天动力研究所液体火箭发动机技术重点实验室，西安 710100；3.航天推进技术研究院，西安 710100；4.西北工业大学 力学与土木建筑学院，西安 710072)

周期性多孔结构以其轻质高强等优异的力学性能和减振、能量吸收等多功能特性而受到国内外诸多学者的广泛关注[1]，在航空航天[2-3]、兵器[4]、船舶[5]等工业中有着非常广泛的应用。在这些工程应用中，多孔结构常常会承受长期振动等载荷[6]，且振动分析中得到的固有频率和模态振型是结构设计中非常重要的参数[7]。因此，周期性多孔结构的振动分析很有必要。

国内外许多学者对周期性多孔夹芯结构的振动行为进行了大量的研究。在对蜂窝、波纹等传统多孔结构的研究中，Kumar等[8]使用有限元法研究了蜂窝夹芯结构的振动性能，认为蜂窝芯子采用硬铝比软橡胶的固有频率高。袁文昊等[9]研究了波纹夹芯板结构的振动性能，认为波纹板结构随芯子壁厚的增加基频逐渐减小，不存在极值点。Zhang等[10]通过理论、试验和仿真方法研究了蜂窝-波纹混杂芯子结构的自由振动行为，认为蜂窝的填充增强了结构刚度，减少了局部模态及变形。点阵结构是一种新型周期性多孔结构，相比波纹和蜂窝等多孔结构，质量更轻，设计方式更灵活，是近年来多孔结构研究方向的热点。在点阵结构的振动性能研究方面，Guo等[11]基于 “折线”模型，研究了金字塔点阵夹芯板结构的固有频率特性，认为随着芯子高度的增加固有频率先增加后减小。钱若力等[12]研究了金字塔结构的固有频率随面板厚度的变化情况，认为一阶随厚度的增加出现波动情况，二阶和三阶均不断增加。Li等[13]认为双层金字塔点阵结构中固有频率随面板厚度增加而减小。上述关于点阵结构振动性能的研究以金字塔等简单构型为主，边界条件主要是简支，对较复杂胞元和其他边界条件下点阵结构的振动行为的研究较少。此外，不同多孔结构关于结构参数对固有频率的影响结论也不同。

BCC(体心立方)点阵结构是一种弯曲主导型点阵结构，在抗冲击和吸能方面性能优异[14]。近年来，由于增材制造技术的发展，其制造得以成熟和便捷，因此也成为研究的热点。在BCC点阵结构的振动研究方面，Kohsaka等[15]理论推导了多层BCC胞元的等效剪切模量，使用理论和有限元法研究了其在简支边界下的一阶固有频率，但尚未经过试验验证，且简支边界在工程应用中极少见到。在含固支边界的振动研究方面，Monkova等[16]测试了不同体积率下BCC点阵结构的振动阻尼性能。Zhang等[17]测试了BCC夹芯板组成卫星结构的振动性能，认为相比蜂窝夹层板，BCC点阵夹层板的比刚度、比强度和抗振性能更好。Z向增强的BCCZ点阵结构相比BCC点阵结构在能量吸收和承载等力学性能方面优势明显[18-19]。Rosa等[20]测试了BCC-XYZ三向边界增强点阵结构的振动阻尼性能，点阵的阻尼性能比实体结构更好。然而，上述研究多是通过试验和仿真手段获得振动性能，并未通过理论模型给出BCC点阵结构的振动机理。同时，材料性能和几何参数均会影响点阵结构的振动频率，但关于这些参数对BCCZ点阵结构振动性能影响的研究，目前还没有公开发表的文献。

随着增材制造点阵结构的广泛应用，其振动性能亟需研究。本文通过试验、理论和有限元方法研究了增材制造钛合金BCCZ点阵结构夹芯梁结构在悬臂边界条件的振动性能，并研究了芯子直径、芯子高度、面板厚度等几何参数和不同材料对其振动特性的影响规律。

1 试验及有限元模型建立

1.1 振动试验

BCCZ点阵单胞的胞元构型如图1所示，单胞的长宽高分别为Lx、Ly和Lz，胞元半径为Rc。基于BCCZ单胞，设计并制备的悬臂边界下的点阵夹芯梁试验件。单胞为立方体构型，设计尺寸为边长4 mm，杆件直径为0.4 mm，结构的整体外形设计尺寸为200 mm×48 mm×10 mm，试件几何模型和打印试件分别如图2(a)和图2(b)所示。其中，上下面板的厚度均为1 mm，芯子为两层，总厚度为8 mm，为固支约束起见，将一端打印为实体结构，长度20 mm，因此点阵夹芯结构的尺寸为180 mm×48 mm×10 mm，其中，长度方向分布45个单胞，宽度方向分布12个单胞，厚度方向分布2个单胞。点阵夹层结构试件由BLT-S400增材制造设备制备，采用SLM(选择性激光熔融)技术。打印参数为：激光功率为250 W，激光扫描速度为1 m/s，铺粉层厚度为50 μm。材料为TC4钛合金，材料试验测试其弹性模量为113.8 GPa，泊松比0.3，材料密度为4 430 kg/m3。

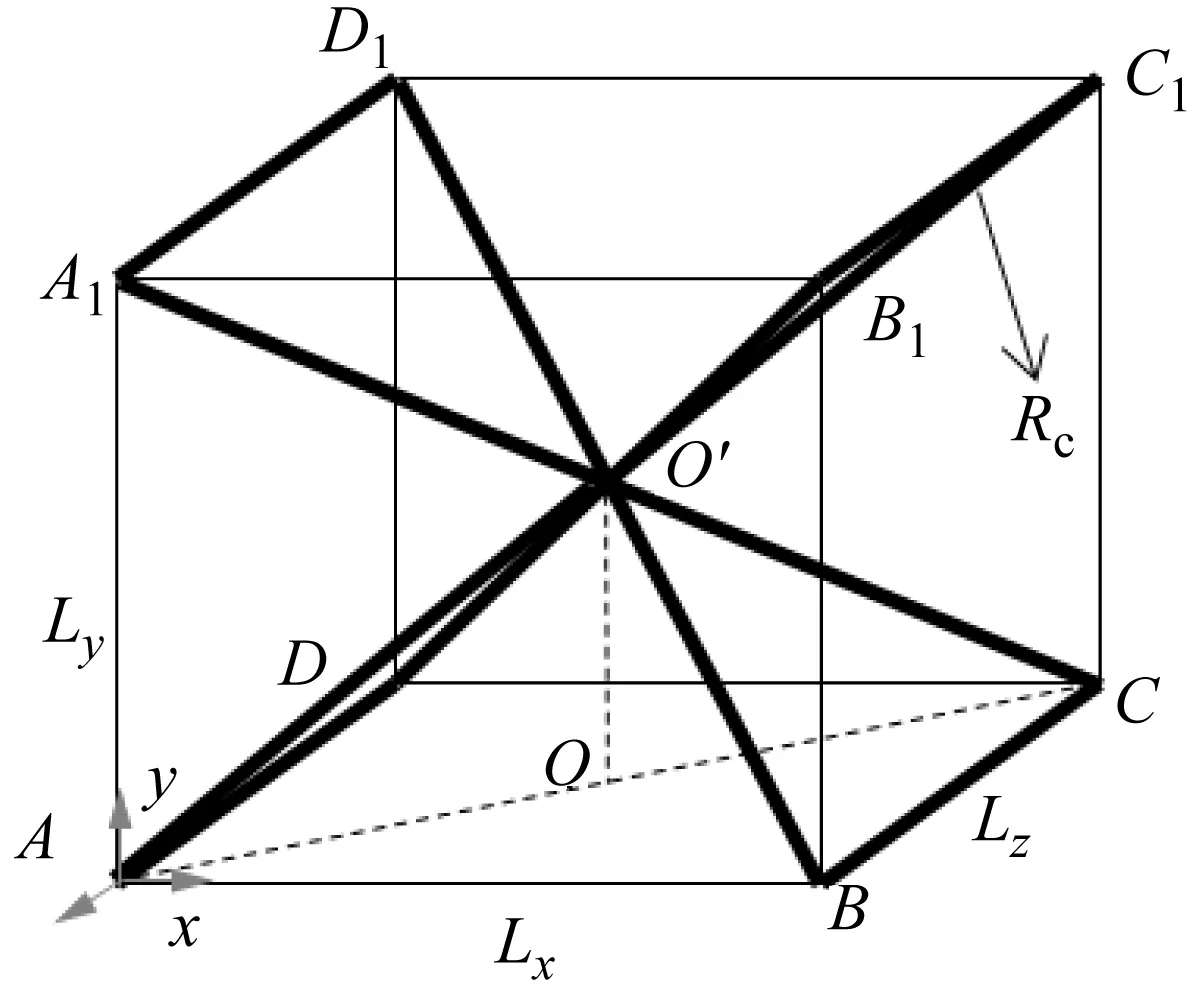
图1 BCCZ增强点阵胞元构型Fig.1 Enhanced BCCZ lattices configuration

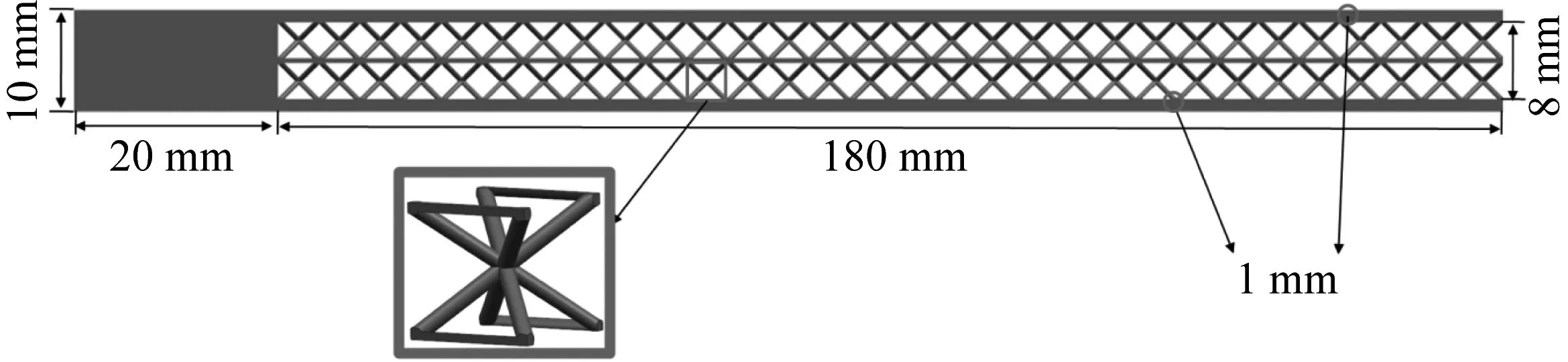
(a) 几何模型

采用力锤敲击获得夹芯板结构的自由振动模态，试验原理如图3 (a)所示，模态试验设备如图3 (b)所示，夹芯板振动试验状态如图3 (c)所示，试验件一端固支在夹具上，一端自由。采用的振动模态分析设备为LMS动态信号分析仪，力锤制造商为欧洲B&K公司，型号为8206，灵敏度为1.041 mV/N。传感器采用压电加速度计，制造商为DYTRAN，型号为3133A1，灵敏度为10 mV/g。为消除边界条件对试验模态频率的影响，采用力矩扳手控制固支端的螺栓拧紧力矩，经过通过不同力矩下的模态试验分析，采用40 N·m的拧紧力矩后模态频率数基本相差不大。

(a) 试验测试流程

采用单点激励多点响应锤击法，首先，在点阵夹芯结构试件表面上标记8个点，用环氧树脂胶粘贴传感器。设定仪器相关参数，然后用力锤对试件进行敲击，在保证良好相干性的前提下对敲击点平均敲击三次后取平均值，敲击产生的信号通过力传感器传到电荷放大器，放大后直接输送到动态信号分析仪，通过快速傅里叶变化后处理分析，以频率分辨率0.5 Hz完成垂直激励方向的模态试验，获得频响函数和试验件的固有频率、振型等相关的模态参数(2 000 Hz以内)。

试验得到的频响函数和振型如图4和图5所示，由于主要研究夹芯梁状点阵结构在悬臂边界下的动态性能，故模态试验振型提取纯弯曲振型，对其他扭转等板状结构特征的振型模态暂不考虑。下文中的不同阶数下的固有频率均指弯曲模态下的排序频率。试验中测得的一阶弯曲固有频率为260.5 Hz，二阶弯曲固有频率为1 546.71 Hz。

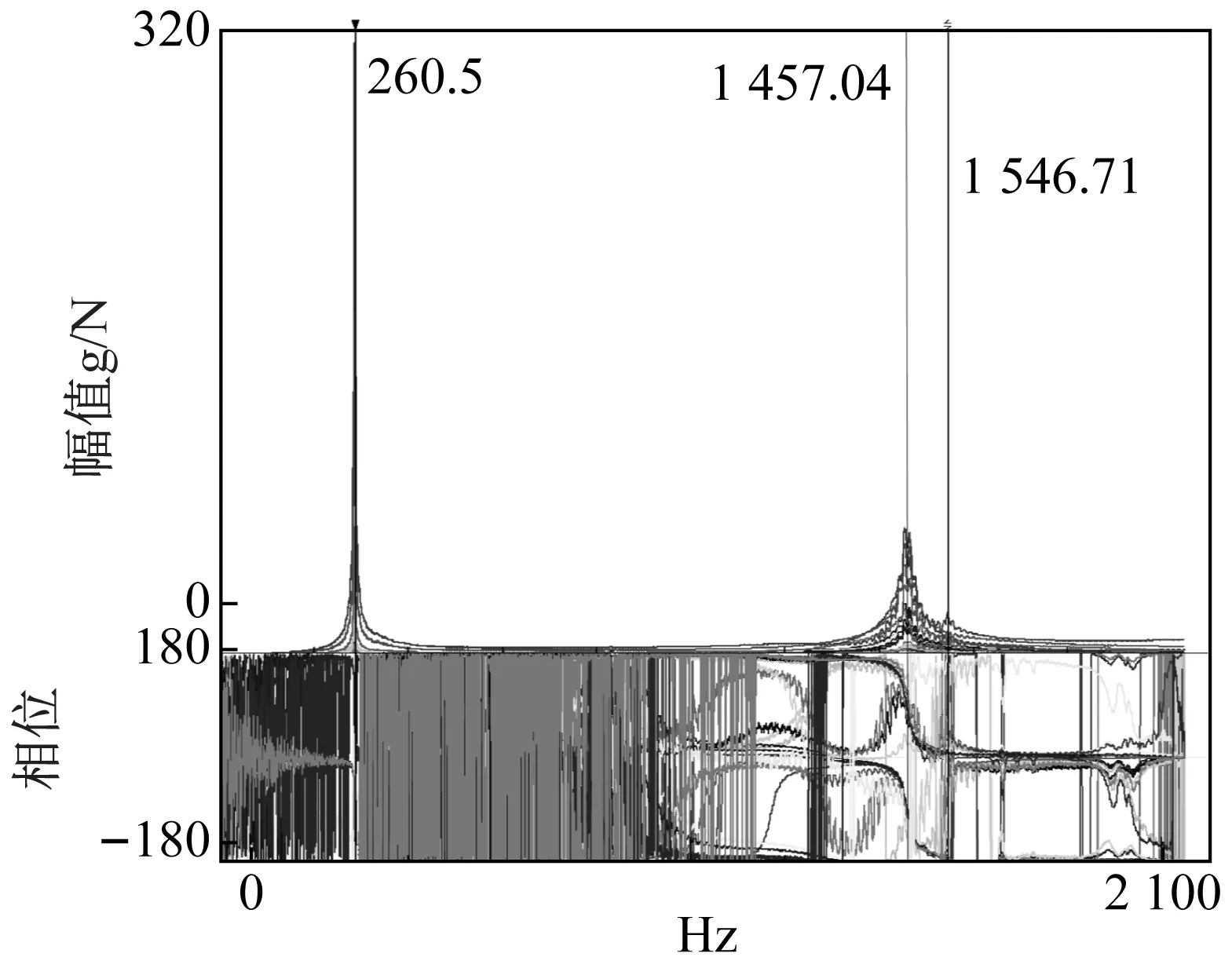
图4 悬臂边界BCCZ点阵结构频响函数Fig.4 Frequency response of BCCZ lattice structures under cantilever boundary

(a) 一阶弯曲模态

1.2 有限元模型

按照试验件尺寸建立有限元模型，采用ABAQUS软件的frequency模块进行模态分析，选用Eigensolver Lanczos求解器，上下面板为4节点壳单元S4R，中间芯子为2节点B31梁单元，固支端建立为实体solid C3D8R单元(八节点线性六面体缩减积分单元)，并进行固支约束，实体与点阵芯子和面板均采用tie连接，点阵芯子和上下面板也使用tie连接，整体结构通过单个胞元阵列产生，然后采用“merge”共节点方式连接芯子中所有点阵节点。有限元数值计算得到的模态振型如图6所示。有限元仿真计算出的一阶、二阶、三阶和四阶弯曲固有频率分别为269.93 Hz、1 443.5 Hz、3 377 Hz、5 467.5 Hz，对比有限元与试验得到的固有频率和振型结果，可知，悬臂边界下试验与有限元数值模型得到的模态振型及固有频率均比较吻合，验证了有限元数值模型的准确性。试验结果与有限元结果的差异，可能是因为增材制造点阵结构杆径分布不均匀、试验边界条件与仿真条件不完全相同或高频下传感器误差增大等原因导致。然而，两者最大相对误差小于7%，可以满足工程中模态频率研究的要求。

(a) 一阶弯曲模态

2 理论模型

基于Lou等[21]提出的“改进折线法”位移假设，使用哈密顿原理，可推导出悬臂状态下夹芯梁结构的振动微分方程如式(1)所示

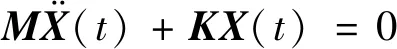
(1)

式中，M和K分别为夹芯梁结构的质量矩阵和刚度矩阵。

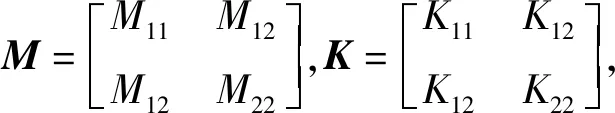
(2)

式中:B和L分别为夹芯梁结构的宽和长;ρf和ρc分别为面板的密度和芯子的等效密度;hf和hc分别为面板和芯子的厚度;Es和Gxz分别为基材的弹性模量和芯子的等效剪切模量。

ζ和ε分别为满足边界条件的位移和转角的振型函数，根据Guo等，表达式如式(3)所示

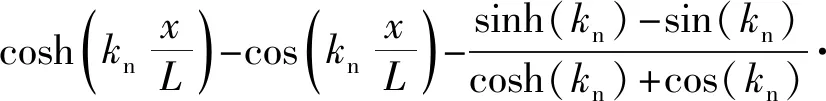
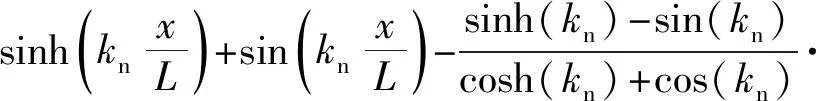
(3)

式中，n为模态阶数。kn前三阶为2.084，4.694，7.855，后面的高阶模态值为(2n-1)π/2。

BCCZ点阵结构的相对密度如式(4)所示。

(4)

(5)

根据Zhang等[23]对多层BCC点阵夹芯结构的等效剪切模量研究，有无面板边界约束状态下BCC点阵结构的等效剪切模量分别如式(6)和式(7)所示。而在沿芯子厚度方向的点阵结构数量很少时，BCCZ点阵结构在上下面板及增强杆边界的约束下，其剪切变形行为可以等效为有边界约束条件下的剪切变形

(6)

(7)

使用式(1)～式(6)的悬臂边界的公式计算得，理论公式计算出的一阶、二阶、三阶和四阶弯曲固有频率分别为261.2 Hz、1 518.6.5 Hz、3 418.3 Hz、5 422.8 Hz。将试验、理论和数值仿真结果计算得到的固有频率比较如表1所示。可以看出，试验和理论模型的最大相对误差为2.69%，理论与有限元仿真模型的最大相对误差为5.2%，平均相对误差2.62%。试验、理论和数值求解计算得到的BCCZ点阵结构夹芯板结构在悬臂状态下的各阶频率基本一致，验证了理论模型、数值模型的准确性。

为了比较有无面板的边界条件下的等效剪切模量对其固有振动频率的影响，将式(7)中的Gxz,uncon代入理论模型计算，一阶、二阶、三阶和四阶频率分别为126.2 Hz、438.6 Hz、762.5 Hz和1 181.5 Hz，与试验和有限元仿真结果差距均较大，无上下面板的芯子结构的固有频率远小于有上下面板的情况，说明上下面板的边界约束对BCCZ点阵夹芯结构的振动性能影响明显。

表1 悬臂边界BCCZ点阵结构模态频率对比Tab.1 Comparison of modal frequencies on BCCZ lattice structures under cantilever boundary

3 结果与讨论

3.1 几何参数

采用理论和有限元方法研究几何参数对悬臂状态下BCCZ点阵夹芯梁结构动态力学性能的影响规律。为体现点阵结构在固有频率方面相比实体结构的优势，采用频率参数η定义结构的振动质量效率，η=f/fs，其中，f为夹芯结构的固有频率，fs为相同长度、宽度、质量和边界条件下相同材料的实体结构的固有频率。

3.1.1 胞元直径

保持BCCZ点阵夹芯结构其他几何参数不变，设置半径为0.1、0.2、0.3、0.4、0.5 mm，得到其固有频率与杆件半径的变化关系如图7所示，其中Sim表示仿真计算结果，Ana表示理论计算结果，Mode 1、2、3、4分别表示第一、二、三、四阶，下同。由图7(a)可以看出，随着杆件半径的增加，BCC点阵结构的各阶固有频率呈现出先增加后减少的趋势，半径为0.2 mm时一阶固有频率最大，其余阶数半径为0.3 mm时最大。由图7(b)可以看出，随着杆件半径的增加，BCCZ点阵结构的一阶频率参数逐渐减小，而其余各阶频率参数呈现出先增加后减少的趋势，一阶频率参数最高，说明一阶固有频率下点阵夹芯结构的振动质量效率最高，所有的频率参数均大于1，反映出点阵夹芯结构在动态力学性能方面相比传统实体结构优势明显。理论解与数值仿真解相比误差较小，验证了理论模型的准确性。

3.1.2 面板厚度

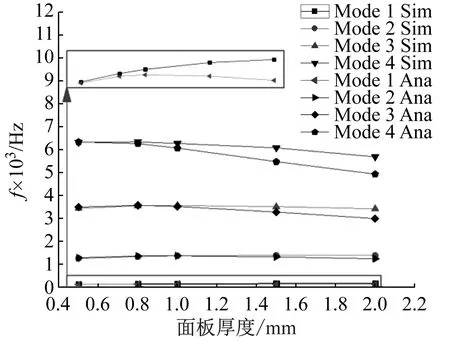
保持直径0.3 mm不变，改变面板厚度，研究面板厚度对悬臂边界条件下BCCZ点阵夹芯结构固有频率的影响。设置面板厚度分别为0.5、0.8、1、1.5和2 mm，得到其固有频率、频率参数与面板厚度的变化关系如图8所示。当面板厚度逐渐增大时，理论求解与数值仿真求解误差逐渐增大，这是由于理论模型假设为薄面板，而厚面板已经逐渐不满足假设条件，故使用有限元方法研究厚度的影响。

由图8(a)可知，随着面板厚度增加，结构的低阶固有频率有所提升，高阶固有频率下降。但是由图8(b)可知，随着面板厚度的增加，夹芯结构整体的频率参数均降低，说明增加面板厚度会降低夹芯结构动特性的结构质量效率。因此，如果要提高BCCZ点阵夹芯梁结构整体的固有频率特性，单纯增加面板厚度虽然会略微有效，但是会增加大的结构附加质量，导致结构的频率参数下降。

(a) 固有频率

3.1.3 芯子高度

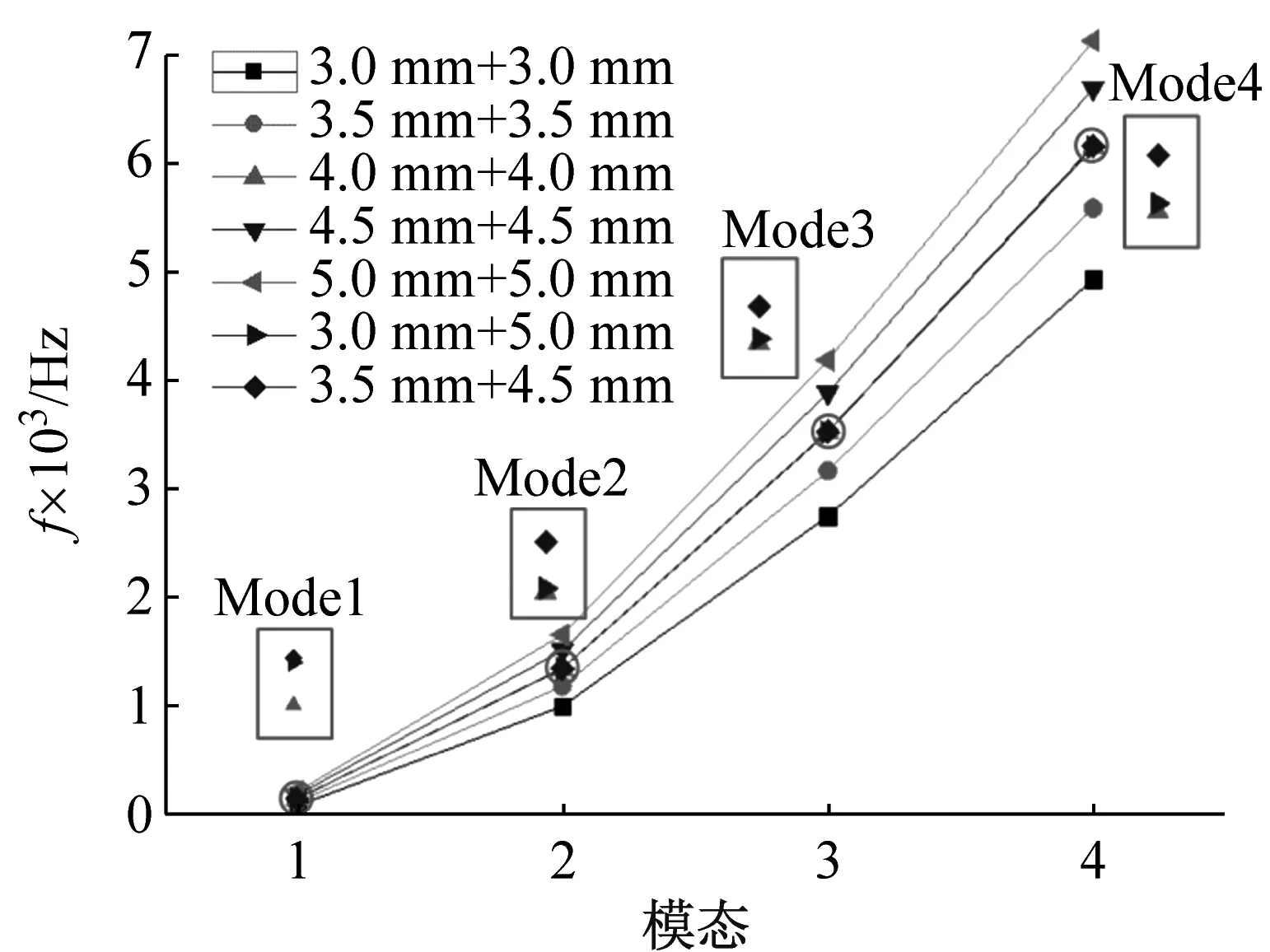
保持芯子胞元底面面积为4 mm×4 mm不变，改变胞元高度，芯子高度依次为3、3.5、4、4.5和5 mm。芯子为两层，杆件半径为0.3 mm，面板厚度为1 mm。不同芯子高度下BCCZ点阵夹芯结构的固有频率如图9所示。由图9(a)可知，随着芯子高度的增加，其结构频率也在不断增加，原因是芯子高度增加了结构的惯性矩。由图9(b)可知，随着芯子高度的增加，其频率参数也在不断增加。其中，一阶频率参数增加最明显。对比梯度高度组合下的点阵结构的性能，对于芯子高度“4 mm+4 mm”组合，设计总高度相同的两种梯度组合形式“3 mm+5 mm”和“3.5 mm+4.5 mm”，对比这三种形式的点阵结构的频率可以看出，梯度组合形式的点阵结构可以实现更高的各阶结构频率和频率参数。其中，“3.5 mm+4.5 mm”组合形式最好，“3 mm+5 mm”组合稍优于“4 mm+4 mm”组合。总体来看，通过梯度形式的设计，可以在不增加整体结构尺寸和不明显增加结构总体质量的情况下提高结构的固有频率及频率参数，但需要对其梯度设计参数进行优化设计。

(a) 固有频率

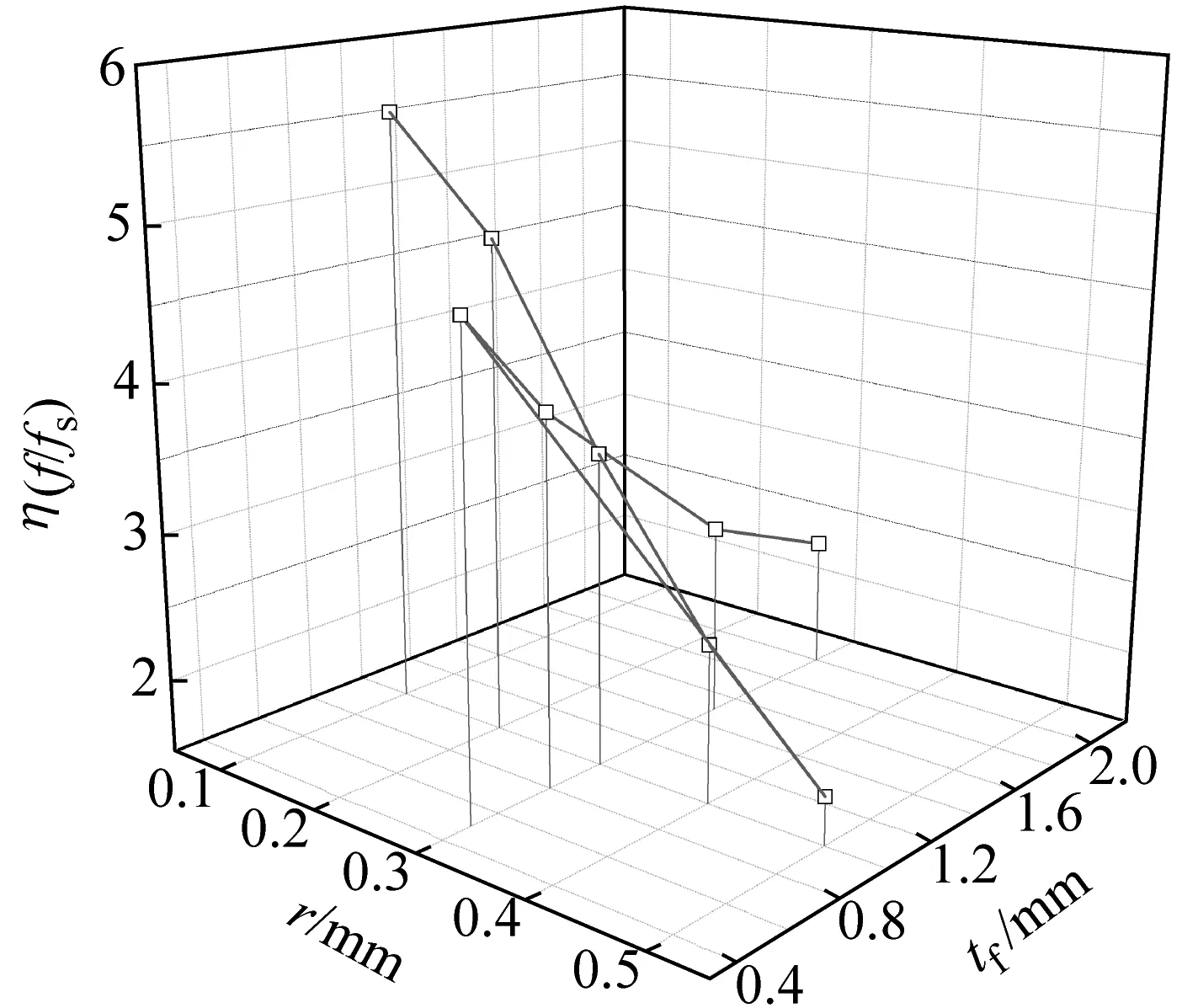
通过对三种几何参数的分析，由于结构参数会导致结构质量的变化，故采用无量纲化的一阶频率参数来衡量三种结构参数对固有频率的影响。图10(a)为胞元半径、面板厚度的一阶频率参数对比，图10(b)为面板厚度、芯子高度的一阶频率参数对比。由图10(a)可知，胞元半径为0.1 mm和面板厚度1 mm组合优于胞元半径0.3 mm和面板厚度0.5 mm组合，且随着尺寸的变化，胞元半径的梯度变化更大。由图10(b)可知，面板厚度0.5 mm和芯子高度4 mm组合优于面板厚度1 mm和芯子高度5 mm组合，且面板厚度的梯度变化更大。因此，改变相同的尺寸数值下，减小胞元半径对一阶频率参数的提高最明显，减小面板厚度次之，而增加芯子高度影响最小。

(a) 固有频率

(a) 半径(r)-面板厚度(tf)

3.2 材料性能

当前，航空航天工业中增材制造常用的金属材料主要包括高温合金，钛合金和铝合金等，分别选取三种材料系列典型的牌号进行振动性能对比分析，包括钛合金系的TC4材料、高温合金系的GH4169材料和铝合金系的AlSi10Mg材料，三种材料的比刚度基本相当。选用牌号的材料性能如表2所示。而双金属材料的增材制造技术已经逐渐成熟[24]，因此，基于不同材料的面板及芯子结构的增材制造也成为可能。

研究不同的芯子面板材料组合对夹芯结构振动性能的影响，按照面板和芯子材料的分布不同，夹芯板可以得到27种材料组合，根据上下面板的对称性，简化后得到18种组合方式。由于一阶频率在振动性能中最为关注，因此，以一阶固有频率为衡量指标。芯子半径为0.3 mm，高度为双层共8 mm，面板厚度为1 mm，其余结构尺寸及边界条件等均与上节相同，为了横向比较不同材料的性能，采用一阶比固有频率概念，为一阶固有频率除以结构质量(不含悬臂实体端)。计算结果如表3所示，表中材料TC4用Ti表示，GH4169用GH表示，AlSi10Mg用Al表示。由表3可知，当芯子为Al时，其一阶固有频率和一阶比固有频率优于芯子为Ti和GH。当使用GH材料时其动态力学性能均较差。当面板-芯子-面板材料组合顺序为Ti-Al-Ti时，一阶固有频率最高；而当材料均为Al或组合为Ti-Al-Al时，其一阶比固有频率较高。因此，采用比刚度较高的面板和密度小的芯子材料可以获得较高的振动频率，而如果追求质量效率最高，则要选择密度最小的全铝材料组合。

表2 增材制造典型材料性能Tab.2 Typical material properties of additive manufacturing technology

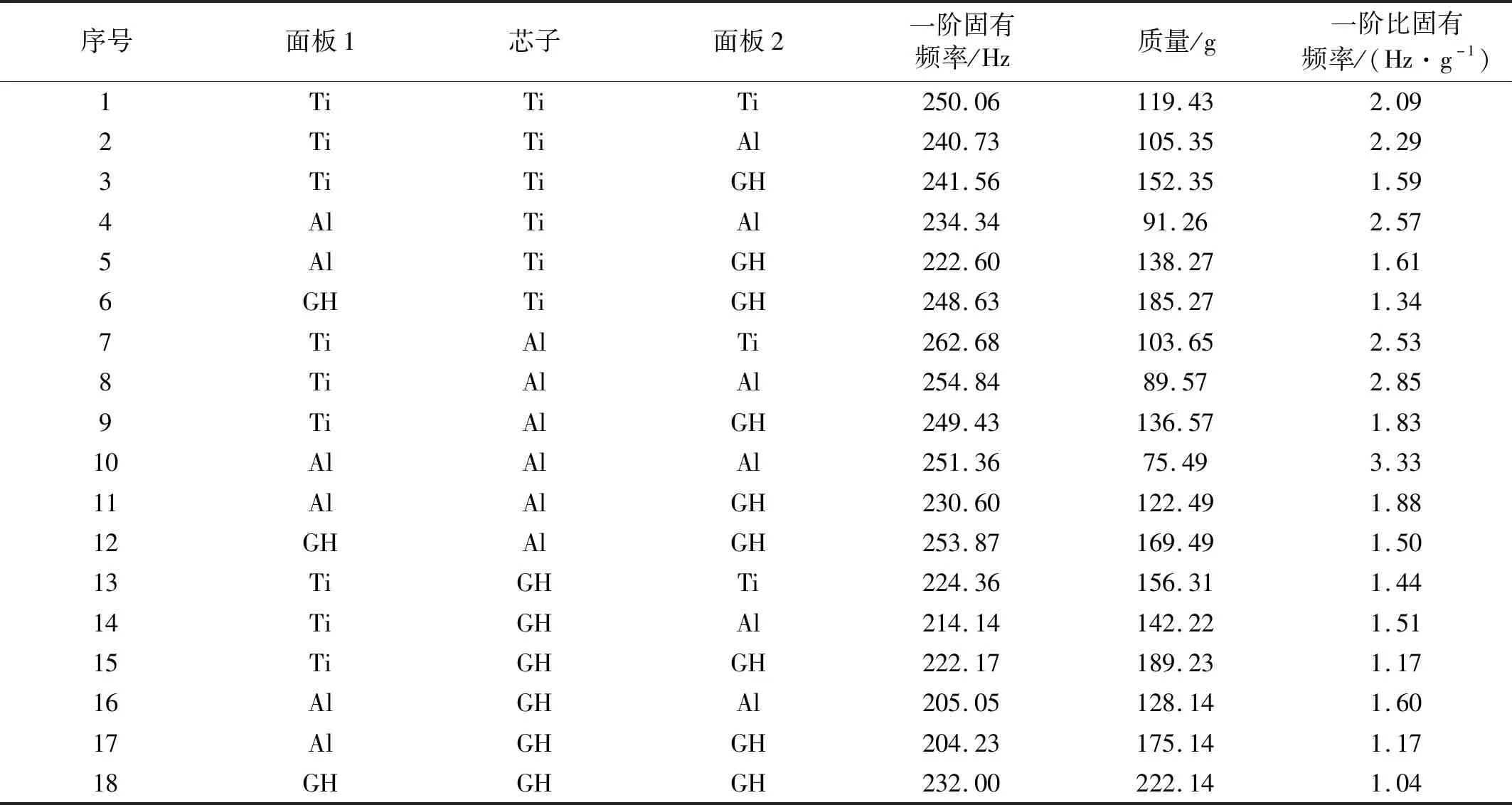
表3 不同材料组合下BCCZ点阵夹芯梁结构固有频率Tab.3 Natural frequency of BCCZ lattice sandwich beams with different material combinations

4 结 论

本文通过理论、有限元仿真和试验方法研究了悬臂边界条件下双层BCCZ点阵夹芯梁结构的振动力学性能，结论如下：

(1) 对比有限元仿真和试验结果，本文提出的自由振动理论模型可以准确预测悬臂边界下BCCZ点阵夹芯梁结构的固有频率。

(2) BCCZ点阵夹芯结构的几何参数对其振动性能影响明显。随着杆件半径的增加，BCC点阵结构的一阶频率参数逐渐减小。面板厚度的增加虽然会增强结构的振动性能，但是会增加结构附加质量，导致夹芯结构整体的频率参数降低。随着芯子高度的增加，其结构频率和频率参数均不断增加。综合来看，胞元直径对一阶频率参数影响最大，面板厚度次之，芯子高度最小。

(3) 不同的材料组合对BCCZ点阵夹芯梁结构的固有频率影响很大。使用钛合金系的TC4、高温合金系的GH4169和铝合金系的AlSi10Mg这三种不同材料组合形式制备的BCCZ夹芯结构的振动性能中，当面板-芯子-面板材料组合顺序为TC4-AlSi10Mg-TC4时，一阶固有频率最高；而当材料均为Al时，其一阶比固有频率最高。采用比刚度较高的面板和密度小的芯子材料可以获得更优的振动力学性能。