SH波入射下正交各向异性双相介质界面附近圆孔的动应力集中
2023-02-01兰国冠张村峰许华南张剑伟
兰国冠,张村峰,许华南,张剑伟
(1.龙岩学院 资源工程学院,福建 龙岩 364000;2.沈阳航空航天大学 航空航天工程学院,沈阳 110000)
随着工程领域(如石油和天然气勘探与开发、地球物理勘探、地震工程、定量无损检测与探伤(NDT)等)的快速发展,对复杂缺陷与弹性波的散射问题的研究一直是弹性动力学领域内的重要课题。现有的大部分研究成果主要研究均匀且各向同性的介质模型[1-11],而地球的实际介质性质通常是各向异性的。各向异性介质中复杂缺陷引起的位移场比较复杂,较难求解,目前这类问题的研究亦有部分成果[12-22],但多为半空间问题,问题模型也相对简单。目前已知的主要研究方法包括波函数展开法、复变函数法、格林函数法以及边界元法等。
各向异性双相介质界面附近复合缺陷的存在会引起局部应力集中,其产生的散射波场往往与缺陷的各种特征参数有关。目前,关于这一课题的理论研究成果还很薄弱,远远不能满足工程实践的理论指导要求,因此,在作者已发表文献[23]的基础上,采用复变函数理论并结合界面“契合”的思想,引入格林函数,给出了正交各向异性双相介质界面附近圆孔对SH波散射问题的解析解,并讨论了不同参数影响下的变化规律。
1 问题描述
图1给出了正交各向异性双相介质内圆孔对SH波散射问题的解析研究模型,区域Ⅰ为含圆柱形孔洞的正交各向异性半无限空间,区域Ⅱ为均匀各向同性的线弹性半空间。SH波以与水平方向呈αi的角度入射,区域Ⅰ和区域Ⅱ的质量密度和剪切模量分别为(ρ1,μ1)和(ρ2,μ2),设孔洞半径为R。分别建立XOY和X′O′Y′两个直角坐标系,关系如下:
x′=x,y′=y-h
(1)
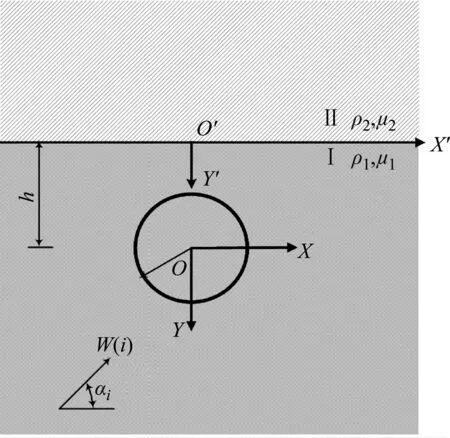
图1 正交各向异性双相介质内圆孔对SH波散射问题的解析研究模型Fig.1 Analytical model of SH wave scattering by a circular cavity in orthotropic biomaterials
2 Green函数
2.1 控制方程
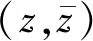
(2)

引入以下形式的变换
(3)
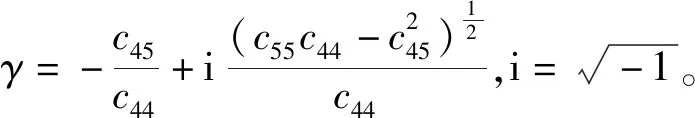
(4)
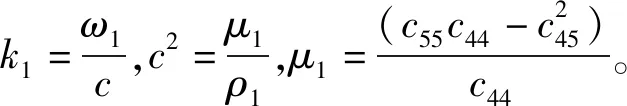
相应的应力表达式为
(5)
其中,
a1=(c55+c44)(1-iγ)+(c55-c44-2ic45)(1+iγ),
c1=(c55+c44)(1+iγ)+(c55-c44+2ic45)(1-iγ),
a2=i(c55+c44)(1-iγ)+(i(c55-c44)+2ic45)(1+iγ),
c2=(i(c44-c55)+2c45)(1-iγ)-i(c55+c44)(1+iγ),
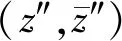
(6)

应力表达式为
(7)
2.2 Green函数G1
如图2所示,在区域Ⅰ的水平界面上任意一点施加时间简谐反平面线源波场,作为本文提出的第一个Green函数G1。
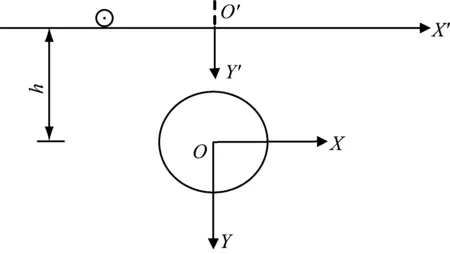
图2 含圆孔的各向异性介质表面作用出平面线源载荷Fig.2 Anisotropic medium model of circular cavity impacted by an out-plane source load on surface
该问题模型的边界条件为
(8)
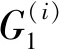
(9)
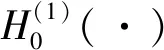
圆孔的激发的散射波G(s)不仅必须满足控制方程(4),而且还必须满足:①水平自由界面处的应力自由;②无穷远处的Sommerfeld辐射条件。对应的表达式为
(10)
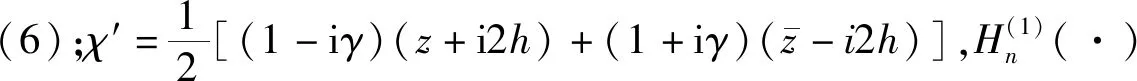
则总波场可表达成
(11)
(12)
其中:
对于求解波场表达式中的待求系数An,采用最小二乘法
(m=0,±1,±2…n)
(13)
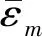
2.3 Green函数G2
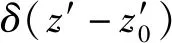
(14)
3 SH波的入射
SH波以αi角度入射后在水平界面Y′=0处发生反射和透射,引入复变量z=x+iy,可将入射波W(i)和反射波W(r)分别表示为如下形式
(15)
(16)
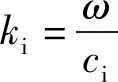
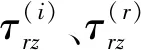
圆孔激发产生的散射波W(s)与2.2节中的G(s)具有一样的表达式和性质,参见式(10)。
4 定解积分方程
至此,区域Ⅰ中的入射波W(i)、反射波W(r)以及散射波W(s)的解析表达式均已给出,从而两个半空间的“剖分”界面y=-h上的总位移场和总应力场亦可得到。
(17)
考虑到界面处切向应力为零的边界条件,波场W(i)、W(r)和W(s)的表达式均严格满足,那么“剖分”界面上的总应力满足如下关系式
(18)
对于区域Ⅱ,“剖分”界面上总位移场与总应力场可表示为
(19)
(20)
如图3所示,由于在水平界面y=-h处位移和应力连续,若将两半空间“契合”,则需分别在区域Ⅰ和区域Ⅱ对应的界面处施加一组未知的外力系F1(r0,θ0)和F2(r0,θ0)。
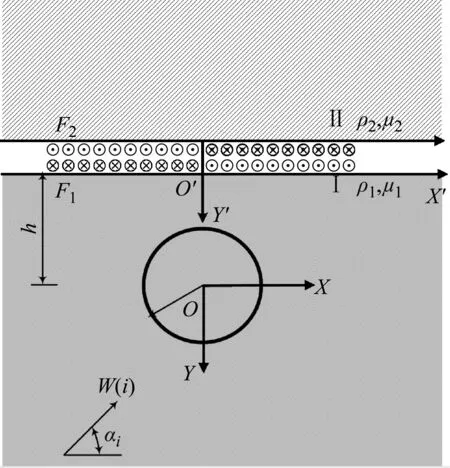
图3 “剖分”界面装配模型Fig.3 The conjunction model of “subdivision”surface
考虑外力系产生的位移场和应力场,可得到两个区域界面处对应的总位移场和总应力场如下
(23)
(24)
其中:G1和G2分别由式(11)和(14)定义。
F1(r0,θ0)=F2(r0,θ0)
(25)
根据界面上位移连续条件,有:
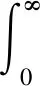
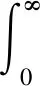
-[W(i)+W(r)+W(s)]θ=π
(26)
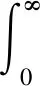
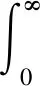
-[W(i)+W(r)+W(s)]θ=0
(27)
上述两个方程属于半无限域上的第一类Fredholm定解积分方程,该方程具有弱奇异性,因此本文选择利用弱奇异积分方程的直接离散方法,将式(26)和式(27)分别转化为线性代数方程组,从而计算出附加外力系F1和F2的值,经验算,可使界面处位移连续的计算精度达10-16~10-17。
5 孔洞周围的动应力集中系数(DSCF)
(28)
6 算例分析
根据以上理论推导,本章提供了大量的计算实例探讨ξ和η(ξ=c45/c55,η=c44/c55)、入射波数k1R、入射角α、孔洞埋深h/R以及两个无量纲参数k2/k1和μ1/μ2等参数对圆形孔洞周边动应力集中系数(DSCF)的影响规律。为了验证本文理论推导的精确性和可行性,将本文问题模型退化为带圆孔的各向异性弹性半空间模型,即文献[12]的分析模型,并令ξ=0.2,η=0.8,h/R=1.5,得出圆孔周边DSCF的变化曲线图如图3所示,经验证,图3的数据结果与文献[12]高度吻合。
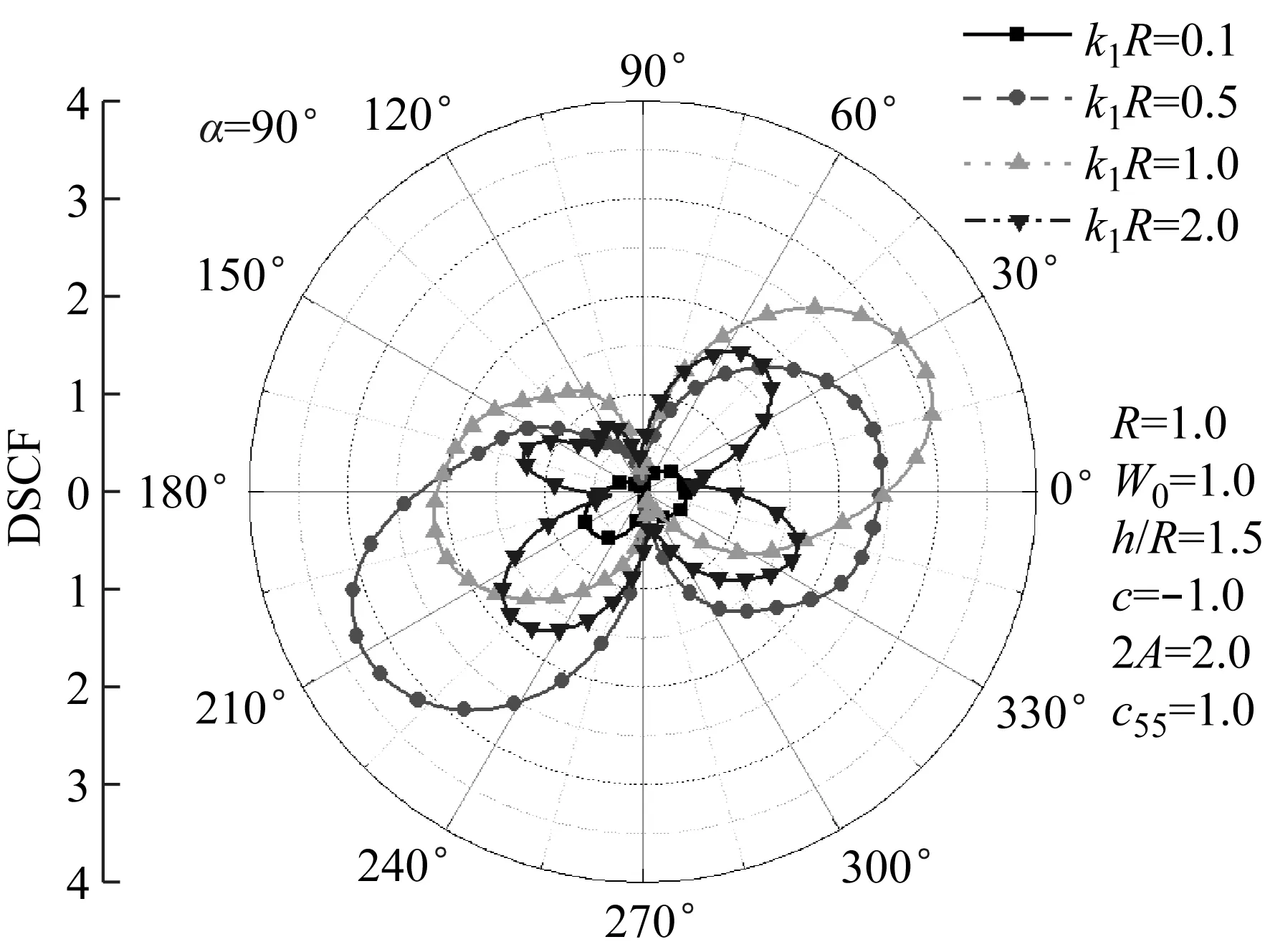
图4 圆孔周边DSCF随k1R的变化(ξ=0.2,η=0.8)Fig.4 DSCF around the cavity with k1R(ξ=0.2,η=0.8)
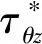
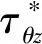
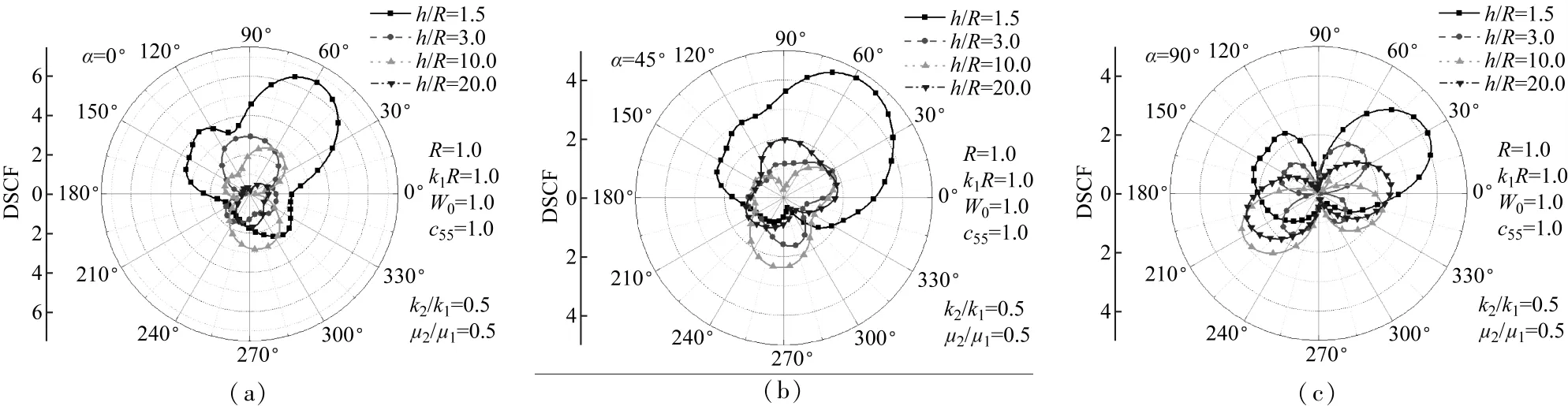
图5 圆孔周边DSCF随h/R的变化(ξ=0.2,η=0.8)Fig.5 DSCF around the cavity with h/R(ξ=0.2,η=0.8)
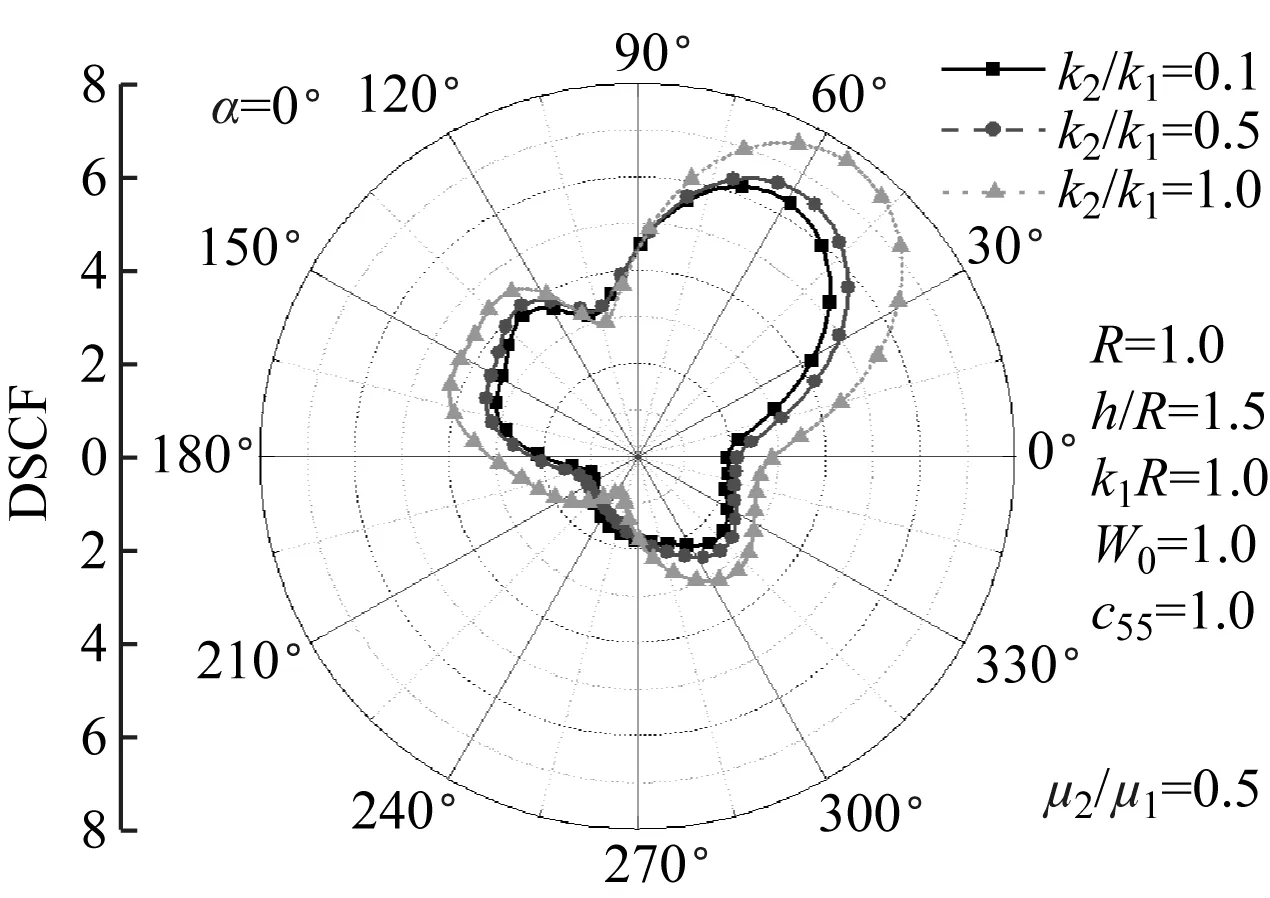
(a)
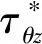
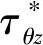
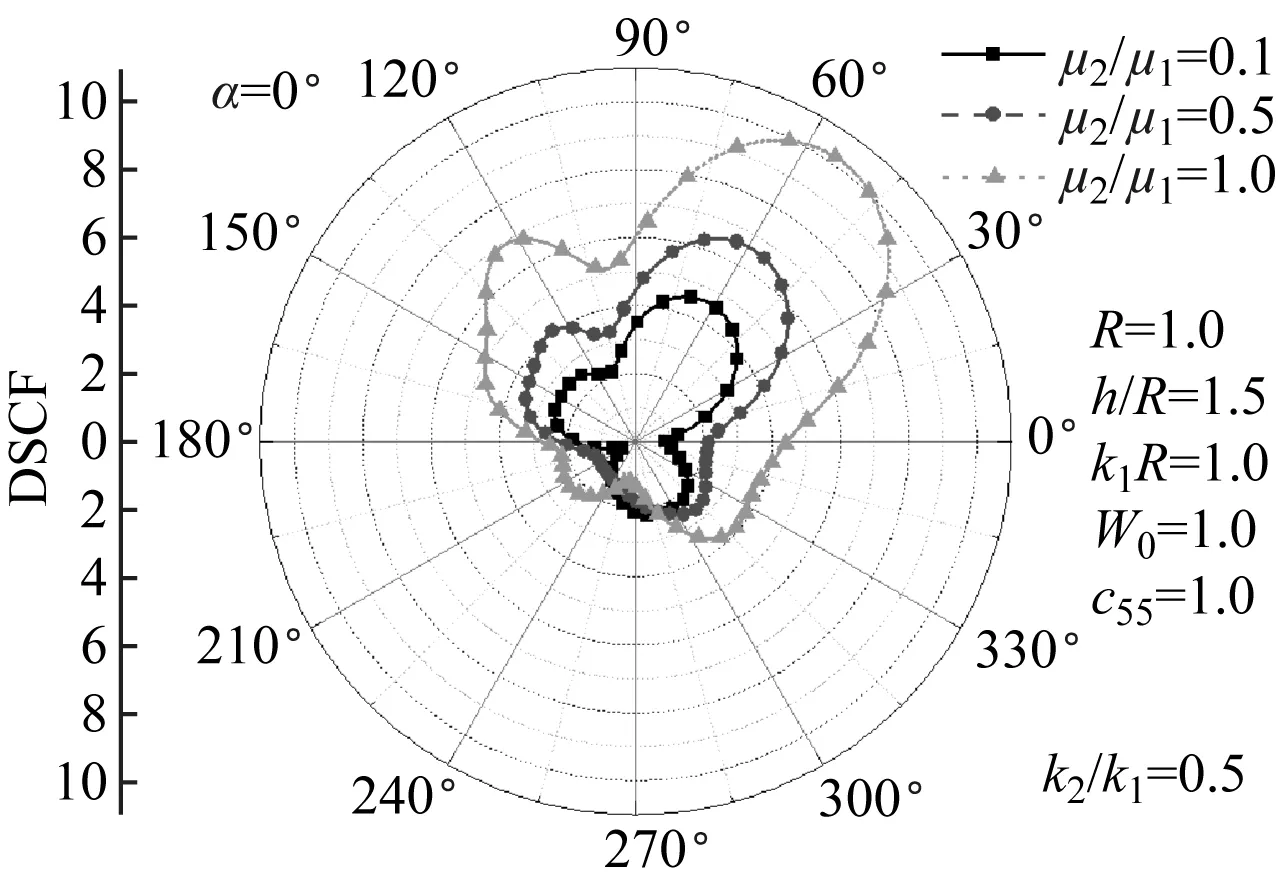
(a)
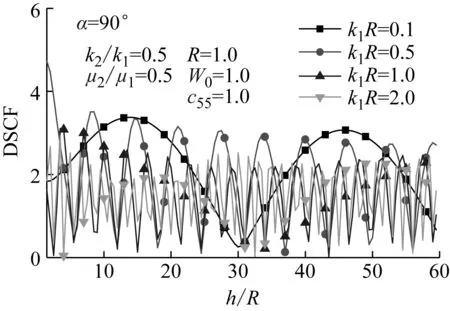
图8 θ=0°处DSCF随h/R的变化(ξ=0.2,η=0.8)Fig.8 Variation of DSCF at θ=0° with h/R(ξ=0.2,η=0.8)
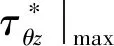
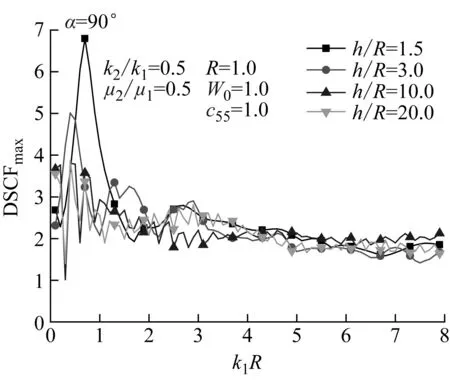
(a) ξ=0.2,η=0.8
7 结 论
本文研究了不同参数下正交各向异性双相介质中圆孔对SH波入射下的动态响应问题。通过详细分析大量算例,得出以下结论:
(1) 入射波频率越大,动应力集中现象越明显。当SH波水平入射和斜入射时,入射波沿各向异性介质的不同方向表现出的传播特性存在差异,孔和界面之间产生的位移场更加复杂,尤其是孔洞深度较浅的情况,动应力集中更剧烈。在工程实践中解决界面问题时,需要重点考虑孔洞埋深、不同介质的波数比和剪切模量比等。
(2) 本文揭示的力学规律对工程实践具有一定的参考价值,有助于材料性能的研究。结合复变函数中的“保角映射”方法,可进一步研究正交各向异性双相介质界面附近的多个不规则形状孔洞、夹杂和多裂纹的动力响应问题。
