考虑反射波震荡的饱和土中大直径现浇混凝土管桩低应变测试解析解

邸同宇，吴文兵，张云鹏，刘 浩

(1.中国地质大学(武汉) 工程学院，武汉 430074；2.中国地质大学(武汉) 浙江研究院，杭州 311305)

桩基纵向振动理论是进行桩基动力设计和低应变检测的重要理论基础，目前国内外学者在桩基纵向振动领域取得了众多研究成果。Winker地基模型[1]是目前在工程实践中被最为广泛应用的一种桩土相互作用模型，该模型通过将桩土相互作用简化为弹簧和阻尼元件实现了桩土相互作用问题的快速求解。但是该模型参数选取依赖于经验和试验，且该离散化的土体模型无法有效反映波在土体中的传播规律。Novak等[2-3]提出了平面应变模型，模型中土体被简化为纵向无主应力差的无限薄层，从而忽略了土体位移在竖直方向的变化，因此该模型只能够反映土体中剪切波的径向传播。通过改进平面应变模型，Nogami等[4]提出了竖向波动模型，解决了土体中纵波沿竖向传播问题。平面应变模型和竖向波动模型由于具备良好的可延展性，因此被广泛应用于桩土相互作用模型推导[5-6]。Wu等[7]和Zheng等[8]先后建立了适用于实心桩和管桩的考虑土体径向位移的真三维波动模型，并用其分析了半正弦脉冲下桩顶的速度时域响应问题。但是，土体材料通常是一种复杂的多相介质，上述理论都假定土体为单相连续介质，忽略了孔隙流体的作用，与真实的桩-土相互作用仍有差距。Biot[9]提出的饱和介质动力固结理论较好地解决了饱和多孔介质的振动问题，且在线弹性范围内可得到严格的解析解，因而被广泛利用。

在桩体振动理论方面，一维杆件模型被广泛用作低应变检测理论的基础，其考虑了应力波在桩身内的纵向传播，对于一般尺寸的桩基测试信号具有较好的解译结果[10-12]。但是，随着大直径桩基的推广应用，应力波在桩身内传播的三维效应已经成为影响低应变测试解译结果的不可忽略的因素[13]。Chow等[14]利用现场试验和有限元方法，发现在对一定直径的桩基进行低应变检测时，检测信号会受到严重的高频干扰，且在反射信号后会出现显著的负向脉冲。为了模拟大直径桩基低应变检测时的三维效应，丁选明等[15-16]、刘浩等[17]、孟坤等[18]、Liu等[19-20]用三维连续介质理论模拟桩身材料，再通过桩土应力边界的连续条件实现桩土微分方程的耦合求解，建立了真三维耦合的桩土低应变测试理论，并发现应力波在桩身内的横向传播和不断发生的界面反射以及局部荷载作用导致的弯曲振动模态是造成高频干扰的主要原因。基于三维连续理论的桩-土耦合低应变理论，其数学求解过于复杂，常常涉及到复平面上超越方程的数值求解问题，尤其在成层地基问题中计算效率较低。不仅如此，三维效应导致的横波干扰已经有了较好的消除方式，对于径向横波可以通过在桩芯和桩壁分别布置的传感器进行双速度叠加进行消除，而对于切向传播的横波则可以通过将激振和接收器布置呈90°来消除[21]。张敬一等[22-23]在桩基低应变检测中采用小波变换法，有效减少了干扰信号的影响，提高了桩底及缺陷段反射信号的拾取精度。因此，现在耗费大量的计算能力以模拟真三维效应已经不是低应变检测的主要需求，相反由于横向惯性效应导致的反射波震荡问题逐渐成为阻碍精确化缺陷识别的又一问题。为了能在有限的计算量下模拟桩土系统内应力波的传播并真实地模拟横向惯性效应，Li等[24]和吴文兵等[25]从能量法的角度修正了一维杆件理论，提出了适用于桩基低应变测试的Rayleigh-Love杆件模型，该模型建模简单，且有严格的完全解析解，具有较好的可编程性。

随着工程建设对桩基承载能力的要求不断提高，大直径现浇混凝土管桩开始得到学者们的重视[26]。与实心桩不同，大直径现浇混凝土管桩在成桩的过程中，管桩内会形成一定高度的桩芯土(亦称“土塞”)，桩芯土的存在使得管桩的承载能力和动力学复刚度得到提升，但也使得其振动情况变得复杂，理论求解的难度也进一步增大[27]。郑长杰等[28]基于分布式Voigt模型模拟桩芯土与管桩内壁相互作用关系，进一步研究了管桩的扭转振动响应解析解；吴文兵等[29]提出了土塞附加质量模型，并在此基础上给出了桩侧土-管桩-桩芯土的纵向耦合振动解析解；刘林超等[30]将桩芯土和管桩内壁之间的相互作用简化成动摩擦作用，并且给出了桩土纵向耦合振动解析解。以上模型中均将桩芯土视为单相介质，而忽略了真实的饱和土体中的土水相互作用，不能反映饱和土体中的真实桩基检测结果。

本文基于轴对称下Biot三维饱和多孔介质理论和Rayleigh-Love杆件模型，建立了三维饱和土中考虑管桩横波效应的桩周土-管桩-桩芯土纵向耦合振动模型，并以此为基础对饱和土中大直径管桩低应变测试时的横向振动导致的反射波震荡进行了研究。

1 数学模型建立

1.1 计算模型

本文研究对象为三维饱和土中的大直径管桩，桩土间相互作用模型如图1所示。管桩高度为H，内外半径分别为r1和r2，桩周土和桩芯土均为单层饱和土，模型中桩周土与桩芯土高度和管桩一致。根据连续模型的基本思想，将桩芯土和桩周土与管桩内外壁之间的相互作用简化为动摩擦力。假设管桩为端承桩，桩顶无位移，同时在桩顶施加激振力p(t)。

1.2 基本假设

(1) 桩侧土与桩芯土为均匀各向同性的三维饱和线弹性体，桩周土体沿径向无限延伸，土体表面均为自由表面，表面上既无正应力也无剪应力。

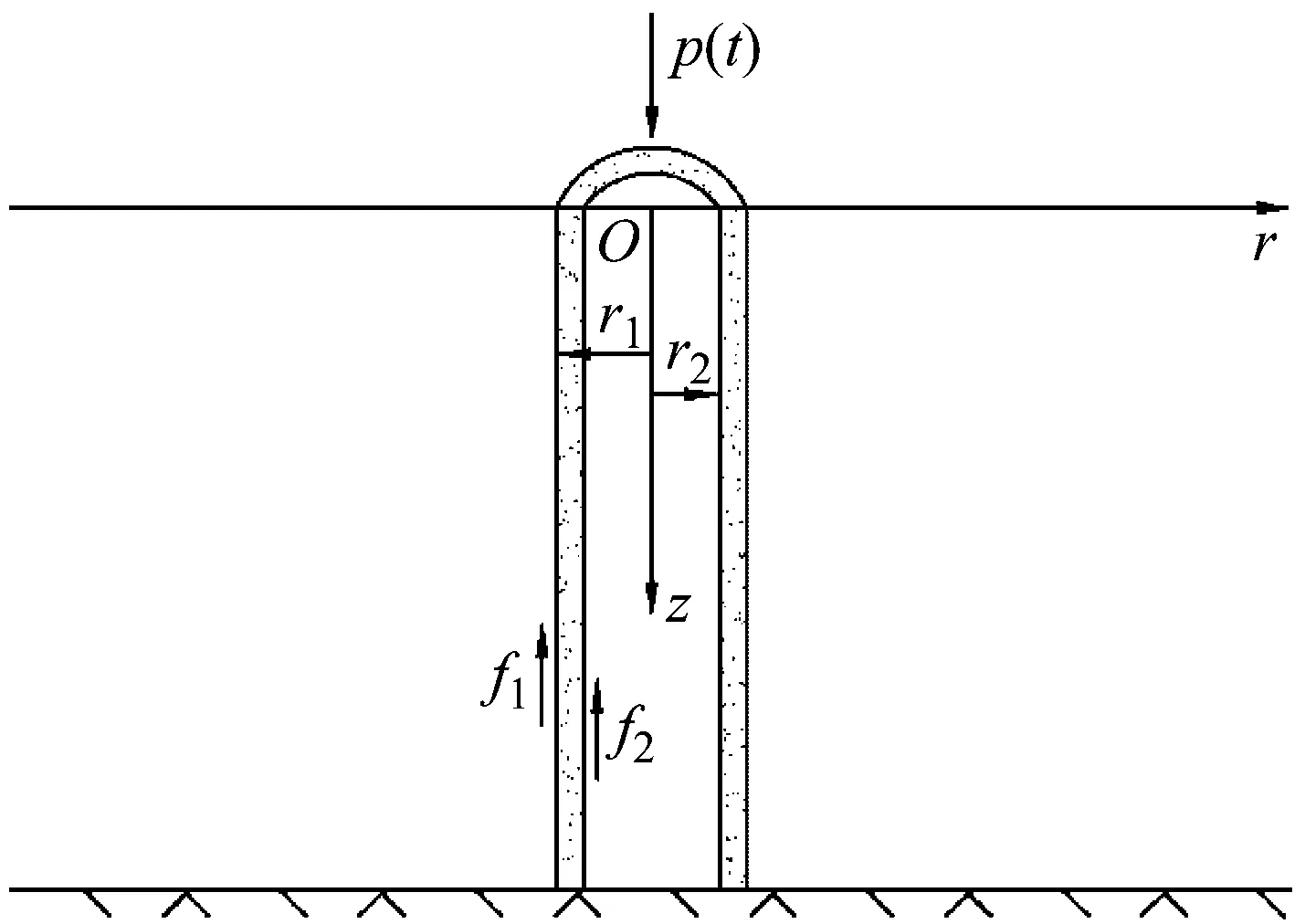
图1 计算模型Fig.1 Computational models

(2) 管桩简化为具有均匀环形截面的黏弹性Rayleigh-Love杆件，其径向位移大小通过能量法和泊松效应进行换算。

(3) 在振动过程中，管桩外壁和内壁分别与桩周土和桩芯土保持完全接触，即桩土界面在整个振动过程中始终保持应力和变形连续，桩土界面无滑移。

(4) 在振动过程中，桩土系统发生的变形满足几何方程的小变形假设。

(5) 系统在初始时刻无任何速度和加速度，桩顶施加的纵向激振是桩土系统发生动力响应的唯一因素。

1.3 控制方程及边界条件

1.3.1 控制方程

(1) 饱和土体振动方程

基于Biot理论建立的饱和土体振动方程如下

(1)

(2)

(3)

(4)

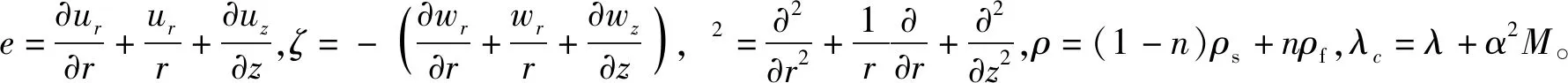
式中：u和w分别表示饱和土体中固相位移和液相相对于固相的位移；r和z分别表示圆柱坐标系中径向方向和纵向方向；λ和μ为土骨架的Lame常数；ρ、ρf和ρs分别表示土体密度、流体密度和土颗粒密度；m=ρf/n，n为饱和土孔隙率，b=η/k，表征流体对土骨架变形的渗透力的系数，η和k分别为流体黏滞系数和流体渗透系数；a和M为表征土体颗粒以及流体压缩性的常数，定义如下

Kd=Ks[1+n(Ks/Kf-1)]

式中，Ks、Kf及Kb分别为土颗粒、流体及土骨架的体积压缩模量。后续标有上标s的方程和变量对应桩芯土，未携带上标的方程和变量对应桩周土。

(2) 管桩竖向振动方程

考虑管桩横向效应后，管桩的纵向振动平衡方程如下

(5)

1.3.2 边界条件

(1) 土体边界条件：

土体无穷远处与中心的径向、纵向位移均为0

(6)

土体表面均为自由界面，纵向应力为0

因此，应对完善本科高校现有的实践教学团队，同时增加双素质教师培养，如成立实践指导小组，由《中级财务会计》专业授课教师和企事业单位的会计人员共同组成指导小组，共同负责、监督实践教学实施。

(7)

桩周土与桩芯土底面边界条件如下

(8)

饱和土孔压边界条件

(9)

(2) 桩土接触界面连续性条件：

(10)

(11)

(3) 管桩桩顶和桩端边界条件:

(12)

(13)

(4) 饱和土与管桩初始条件：

(14)

(15)

2 控制方程求解

2.1 桩周土振动方程求解

为了耦合固相和液相，引入势函数如下

(16)

(17)

(18)

(19)

将势函数代入上述方程，再对时间进行拉普拉斯变换得到以下方程

(20)

(21)

(22)

(23)

将上式表示成矩阵形式

(24)

(25)

(26)

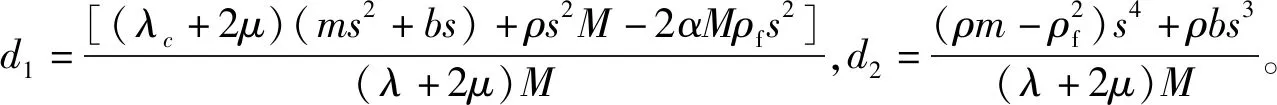
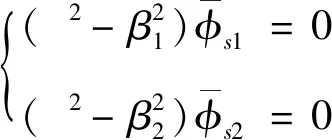
(27)

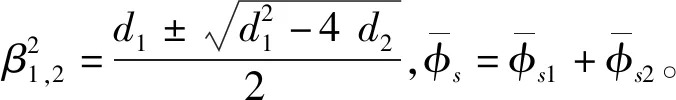
(28)

(29)

(30)

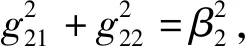
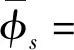
(31)

(32)

(33)

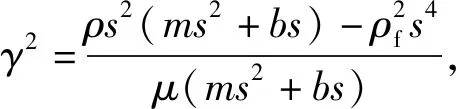
(34)

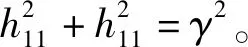
(35)

将势函数代入式(16)～(19)，得到以下结果：

K0(g21r)(C2g22eg22z-D2g22e-g22z)-

(36)

K1(g21r)g21(C2eg22z+D2e-g22z)-

h11K1(h11r)(C5h12eh12z-D5h12e-h12z)

(37)

K0(g21r)(C4g22eg22z-D4g22e-g22z)-

(38)

K1(g21r)g21(C4eg22z+D4e-g22z)-

h11K1(h11r)(C6h12eh12z-D6h12e-h12z)

(39)

结合饱和土边界条件式(7)以及K0(g11r)、K0(g21r)、K0(h11r)之间非线性关系，可以得到如下关系

C1+D1=C2+D2=C5-D5=0

(40)

由土体底面边界条件(8)，可以得到g12，g22，h12同时满足如下方程

(41)

再结合桩土接触界面孔压边界条件(9)，可以得到如下方程

λ1g1nC1nK1(g1nr1)+λ2g2nC2nK1(g2nr1)+

λ5h1nhnC5nK1(h1nr1)=0

(42)

通过式(42)，C5n可用C1n、C2n表示如下

(43)

代入上述待定系数后，桩土接触界面处桩周土纵向表达式可表示为

(44)

其中，

桩土接触面处桩周土剪应力为

(45)

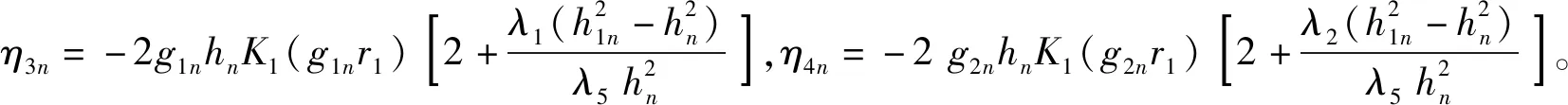
桩土接触面处桩周土水平位移

(46)

2.2 桩芯土振动方程求解

由连续模型可知，桩芯土振动方程与桩周土一致，采用相同的求解步骤，可以得到桩芯土的纵向及径向位移表达式如下

I0(g41r)(E2g42eg22z-F2g42e-g42z)-

(47)

I1(g41r)g41(E2eg42z+F2e-g42z)+

h11I1(h21r)(E5h22eh22z-F5h22e-h22z)]

(48)

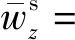
I0(g41r)(E4g42eg42z-F4g42e-g42z)-

(49)

I1(g41r)g41(E4eg42z+F4e-g42z)+

h11I1(h21r)(E6h22eh22z-F6h22e-h22z)]

(50)

式中，E1、E2、E3、E4、E5、E6为待定系数。

结合桩芯土的边界条件，桩土接触界面处桩芯土纵向位移、剪应力及径向位移为

(51)

(52)

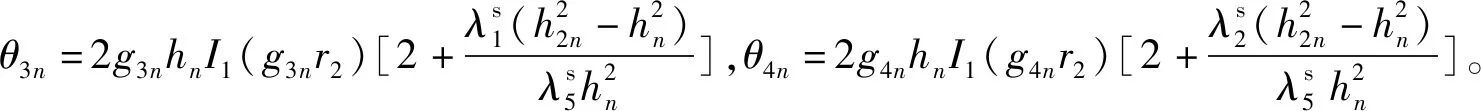
(53)

由式(10)和式(11)可以得到桩周土与桩芯土位移表达式的系数之间具有如下关系

E1n=m1C1n+n1C2n

(54)

E2n=m2C1n+n2C2n

(55)

2.3 管桩振动方程求解

结合初始条件式(15)，对管桩纵向振动方程进行Laplace变换

(56)

式中，Up为up拉普拉斯变换，式(56)的通解为

Up=αeκz+βe-κz+

(57)

由管桩边界条件(12)、(13)容易求得α、β

(58)

(59)

由桩土边界连续条件(10)、(11)以及函数sinh的正交性，求C1n和C2n

(60)

(61)

最后得C1n、C2n：

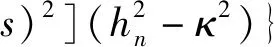
(62)

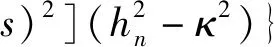
(63)

桩顶的位移阻抗函数为

(64)

桩顶界面处的速度传递函数为

(65)

在式(65)中令s=iω，则得到桩顶速度频域响应函数Hv。当桩顶作用瞬态半正弦脉冲荷载p(t)=Qmaxsin(ω0t)(0≤t≤π/ω0)，可得到桩顶速度时域响应半解析解

(66)

3 模型验证

本文解采用的管桩模型为Rayleigh-Love杆件，当Rayleigh-Love杆件的泊松比取值为0时，本文解退化为一维杆件模型。当管桩内部桩芯土的弹性模量取值为0时，本文解退化为忽略桩芯土的桩周土-管桩纵向耦合振动模型。

讨论中采用的桩土参数为：饱和土密度2 200 kg/m3，土体剪切波速为120 m/s，Ks=36 GPa，Kf=2 GPa，孔隙率n=0.4，泊松比v=0.35，常数α=0.97；管桩密度为2 500 kg/m3，桩身纵波波速为4 000 m/s，泊松比vp=0.3，管桩高度为15 m，内外半径分别为1.0 m、0.8 m；激振荷载ω0=4 000 rad/s。下文的参数分析未作说明时均采用上述参数。

从图2中可以看出，本文解与一维杆件解的曲线趋势大致保持一致。本文解的桩尖反射信号幅值较一维杆件理论有所下降，并且时间上具有一定的滞后性。反射信号幅值的下降是由于在本文解中部分应力波能量发生在了横向变形上，导致本文解的幅值相比于只考虑纵向变形的一维杆件模型发生下降。同时，相对于一维解，本文解较好地考虑了桩底反射波到达桩顶后沿径向散射导致的震荡效应。

图2 本文解与一维杆件解对比Fig.2 Comparison between the paper’s solution and one- dimensional solution

管桩由于存在桩芯土，其纵向振动情况会变得更加复杂。本文假设桩芯土高度与管桩相同，从图3中可以看出，忽略桩芯土模型的桩顶速度时域曲线比考虑桩芯土的模型具有更强的振荡现象，并且桩尖反射信号的幅值更高。此外，桩芯土的存在会导致模型桩的桩顶速度时域曲线在振荡效应结束后具有更高的幅值。综上所述，大直径管桩的纵向振动过程必须要考虑桩芯土对结果的影响。

图3 桩芯土的影响Fig.3 Influences of the presence of pile core soil

4 参数分析

4.1 管桩泊松比对桩顶纵向振动特性的影响

本文建立的模型考虑了桩身横波干扰效应，因此下面详细讨论管桩泊松比变化对管桩纵向振动特性的影响。分别设置管桩泊松比为0，0.1，0.2，0.3。从图4中可以看出，不同管桩泊松比下，管桩的桩顶速度时域响应曲线在桩尖反射信号处具有较大的差异性。随着管桩泊松比的增大，第一次桩尖反射信号会逐渐延迟，并且桩尖反射信号的幅值也呈现逐渐下降的趋势。随着管桩泊松比的增大，第一次桩尖反射信号后的曲线振荡程度逐渐增强。应力波在经过桩尖反射回到桩顶后会产生大量的横波，横波沿径向传播产生了振荡效应。当管桩泊松比越大时，横波的影响越大，桩顶接收到信号振荡效应越明显。

图4 泊松比对桩顶速度响应的影响Fig.4 Influences of Poisson’s ratio on the velocity responseat pipe top

4.2 管桩壁厚比对桩顶纵向振动特性的影响

本文采用的管桩模型为Rayleigh-Love杆件，该模型在分析大直径桩的振动方面具有较好的适用性，因此该部分主要分析管桩壁厚对桩顶纵向振动的影响。分别改变内半径为0.9 m，0.8 m，0.7 m，0.6 m，管桩壁厚分别为0.1 m,0.2 m,0.3 m,0.4 m，得到的桩顶速度时域曲线如图5所示。

图5 壁厚对桩顶速度响应的影响Fig.5 Influences of width of pile shaft on the velocity response at pipe top

从图中可以看到，管桩壁厚对桩尖信号反射前的速度时域曲线影响程度很小，但是对桩尖反射信号的幅值影响较大。随着管桩壁厚增大，桩尖反射信号幅值逐渐提高。这说明在进行桩基低应变检测中，在相同条件下，壁厚较大的管桩更容易接收到桩尖反射信号。

4.3 管桩长细比对桩顶纵向振动特性的影响

图6为管桩长细比对桩顶速度时域曲线的影响，讨论中保持管桩高度，壁厚不变，分别改变管桩外半径。从图中可以看到，随着管桩长细比的增大，第一次桩尖反射信号没有发生明显的改变，反射信号的宽度稍微减小。随着管桩长细比增大，第一次反射信号后的曲线振荡现象提前。

图6 管桩长细比对桩顶速度响应的影响Fig.6 Influences of slenderness on the velocity response at pipe top

4.4 桩芯土剪切模量对桩顶纵向振动特性的影响

桩芯土的性质一直是桩土系统之间相互作用的重要参数。本文中的桩周土与桩芯土均为饱和土体，为了区别桩芯土与桩周土作用的不同，单独改变桩芯土的剪切模量，分析其对桩顶纵向振动的影响。

图7为Eb/μ分别为500，1 000，1 500时的桩顶速度时域曲线。从图中可以看到，随着桩芯土剪切模量的降低，曲线振荡幅度在逐渐减小，高频干扰的现象也在逐渐减弱。桩芯剪切模量的改变对第一次反射信号的影响较小，但会导致反射信号之后的曲线产生明显的幅度差。

图7 桩土模量比对桩顶速度响应的影响Fig.7 Influences of pile-soil modulus ratio on the velocity response at pipe top

4.5 桩芯土渗透力对桩顶纵向振动特性的影响

表征饱和土渗透能力的系数b分别取0，105,1010时，桩顶速度时域曲线如图8所示。从图8中可以看出，当b=0与b=105N·s/m4,两者的桩顶速度时域曲线很相近，当b=1010N·s/m4时，第一次桩尖反射信号较前者的反射信号幅值有一定程度的下降。

图8 渗透力对桩顶速度响应的影响Fig.8 Influences of osmotic force on the velocity responseat pipe top

5 结 论

本文推导得到了考虑横波干扰的饱和土下大直径管桩的纵向振动解析解。土体由Biot多孔介质连续方程控制，为了考虑大直径桩的桩底反射信号受到横向振动发生的振荡效应，Rayleigh-Love杆模型在本文中用于管桩振动的模拟。通过与经典理论解的对比，本文解的正确性得到了验证，并通过与忽略桩芯土的模型对比，证明了桩土模型考虑桩芯土的必要性。主要结论如下：

(1) 随着管桩泊松比增大，管桩横向惯性效应增强，桩尖反射信号幅值逐渐降低，反射信号宽度逐渐增大，并且在时间上具有延迟的趋势。

(2) 随着管桩壁厚增大，桩尖反射信号幅值增大，反射信号宽度增大，反射信号后的曲线振荡幅值逐渐增大，但随着时间推移，管桩壁厚增大带来的振荡增强现象会逐渐减弱。

(3) 管桩长细比变化对桩顶速度时域曲线影响相对较小，随着管桩长细比的减小，桩尖反射信号逐渐延迟，随着时间的推移，桩尖反射信号后的延迟现象逐渐明显。

(4) 当桩芯土渗透系数逐渐增大时，在b=0和b=105N·s/m4，桩顶速度时域曲线并未发生存在明显变化，当b取值1010N·s/m4时，即桩芯土几乎失去渗透性时，桩顶速度时域曲线的反射信号幅值比之前情况有所下降，这种现象在反射信号之后的振荡曲线中逐渐增强。

(5) 当管桩与桩芯土模量比值增大时，桩尖反射信号幅值呈现微弱的下降趋势，速度时域曲线振荡减弱。