Double sketch：双层计数数据略图的流测量方法

吴慧敏，陈世平，2，梁 坤

1(上海理工大学 光电信息与计算机工程学院，上海200093) 2(上海理工大学 信息化办公室，上海200093)

1 引 言

随着网络业务的快速发展，爆发式增长的数据流量对网络管理提出了巨大的挑战，流量测量成为当前研究的热点.流量测量对于云和数据中心的现代网络管理是不可或缺的.管理员测量各种流量统计数据，如流频率测量，以推断运行网络中的关键行为或任何异常模式.不幸的是，面对海量的网络流量和大规模的网络部署，测量流量统计并不简单.无误差测量需要对每流进行跟踪，然而今天的数据中心网络可以在非常短的时间内拥有数千个并发流，这将需要大量资源来执行每个流的跟踪.同时，真实的网络流是偏斜的，即一小部分流的规模非常大称之为象流，而大多数流的规模较小称之为小流.这些问题给流量测量带来不小的挑战.

流量测量方法主要包括基于采样技术以及基于流技术.在传统的基于采样的方法中，如sflow[1]，netflow1等，只能实现粗粒度的测量，如果要实现细粒度的测量则需要提高采样率，这需要大量的内存空间，且采样对于小流并不友好.基于流技术的方法中，使用数据略图(sketch)来近似记录和估算流数据已成为一种流行.数据略图是一种紧凑的数据结构，具有内存占用小、精度高、插入和查询速度快等特点.目前数据略图被广泛应用于象流检测[2-8]，数据流分布[4，9]，基数估计[4，10]，熵估计[2，4，7，9]，DDOS检测[2]，流大小估计[3，4，6，9，11-16]，重大变化检测[2-4，7，9]，流频率估计[17-22]等流测量任务中.

但是，由于当前流量的是偏斜且高速的，单层数据略图的计数器要足够大，以适应象流，因此小流的计数器高位内存被浪费；多层数据略图使用多个原子数据略图相互调节，其内存分配复杂且高层次略图空间往往被浪费.综上所述，目前基于数据略图的测量方案在速度、内存使用以及准确性的衡量之间仍然还有上升空间.本文的目标是设计一个新颖的数据略图，在保证速度的前提下，对相应的测量任务可达到比现有技术更高的准确性，特别是针对只使用很小的内存处理非均匀分布的网络流量情形.

本文提出名为Double sketch的双层数据略图，主要贡献为：1)提出了一种新的双层数据略图Double sketch，使用单独的辅助结构数据略图，记录计数器满的次数，提高了内存的使用效率.2)使用Double sketch来估算流的数据包数量，以此完成流大小估计和象流检测两个重要的网络测量任务.同时，该数据略图可用于流频率估计.3)本文进行了大量的实验，实验结果表明，本文的数据略图比其它的数据略图有更高的准确性，更快的速度.

2 相关工作

3种典型的数据略图：CM sketch[11]，CU sketch[12]和Count sketch[14]和近年提出的多层数据略图Diamond sketch[14]被广泛用于流量测量.CM sketch由d个数组组成：A1，A2…Ad，其中每一个数组都由w个计数器组成，并且与散列函数hi(.)(1≤hi(.)≤w，1≤i≤d)相对应.当插入流f时，CM sketch首先计算d个散列函数并定位d个计数器：A1[h1(f)]，A2[h2(f)]，…，Ad[hd(f)]，然后它将对应的d个计数器的值均加1.当查询流f时，CM sketch报告d个散列计数器的最小值.与CM sketch相比，CU sketch进行了轻微但有效的修改，即保守更新.在插入过程中，CU草图只增加d个散列计数器中的最小计数器(可能有两个或更多个最小计数器)，而查询过程保持不变.Count sketch也类似于CM sketch，区别在于在Count sketch中每个数组使用额外的散列函数来平滑意外出现的错误.在这些数据略图中，CU sketch在精度和速度方面都表现最好.但是上述的数据略图均存在内存效率低下，在有限内存下准确性较低的问题.

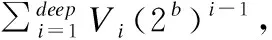
Double sketch与Diamond sketch最相似.在Double sketch中，采用两层数据略图L1与L2层.两个原子数据略图均采用较小的计数器.在执行插入操作时，用L1对应的计数器记录流，当计数器满时，将其置0，同时在L2上插入1，代表满计数器次数增加一次.在执行查询操作时，先查询L2层计数器满的次数为c1，再查询L1层的余包数c2，最终的结果为：c1*2b+c2，其中b为L1层原子数据略图的计数器位数.在执行插入或查询操作时，本文的方法哈希计算少，内存分配简单，各层次协调效果好，这减少了内存浪费，提高的准确性和速度.

3 双层计数数据略图(Double sketch)

在本节中我们将介绍Double sketch的数据结构及其插入与删除操作.同时简要说明该数据结构用于的其他网络流量测量任务.

3.1 基本原理

实际的流量数据是倾斜的，现有的数据略图对这些数据集的估算准确性较低，为了解决这个问题，我们提出了Double sketch，它是由两个原子数据略图组成的新的数据略图.此处的原子数据略图可以是C、CU、CM数据略图中的任意一个，本文采用CU数据略图作为原子数据略图，原因是在算法中频繁执行插入与查询操作，而CU作为原子草图能够获得更高的准确性.

我们首先用一个原子数据略图L1记录流数据包的数量.由于其计数器较小，当遇到数据包个数较多的流时，计数器可能会满，即达到计数器的最大值.当在L1层对应的计数器值达到最大值时，将L1所在的计数器值置为减去对应计数器最大值后的余包量(本文中余包量为0)，然后，在第2个原子数据略图L2中记录当前流填满计数器的次数.这样，对偏斜的流数据集，小流的数据包数量直接存储在L1层，没有发生计数器满的现象，L2层不更新；数据包数量较多的大流，达到计数器的最大值，需要记录填满计数器的次数，更新L2层.当查询流的数据包数量时，分别查询L1和L2的结果，利用L1和L2的结果，可以实现象流和小流的数据包个数的高准确性估计.

3.2 数据结构

表1中记录Double sketch算法中用到的变量及其含义的相关信息.

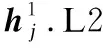
L1层第i个数组的第j个计数器记为L1[i][j](1≤i≤d1；1≤j≤w1)，L2层第i个数组的第j个计数器记为L2[i][j](1≤i≤d2；1≤j≤w2).Double sketch的初始化是将所有的计数器初始值置为0.接下来，我们讨论Double sketch的插入和删除操作.

表1 变量含义表Table 1 Variable meaning table

3.3 插入操作

综上所述，插入操作会出现以下2种情况：1)L1层对应计数器未满.将(f，1)插入到L1层时，所有计数器的值都小于2b1-1，将值最小的计数器值加1，插入结束.2)L1层对应计数器值满.将(f，1)插入到L1层时，所有计数器的值都等于2b1-1，将L1所有计数器的值置0，更新L2，插入结束.

插入操作的伪代码如算法1所示.

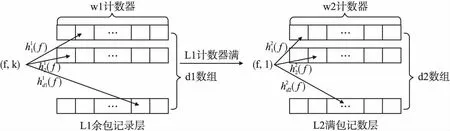
图1 Double sketch数据结构图Fig.1 Data structure of the Double sketch

算法1.Double sketch插入操作

输入：f to insert

1.Function：insert(f)

3.Vmin1←min(S1)

4.ifVmin1=2b1-1 then

5. for each countc∈S1 do

6.c←0

8.Vmin2←min(S2)

9. for each countc′∈S2 do

10. ifc′=Vmin2then

11.c′←Vmin2+1

12.else

13. for each countc∈S1 do

14. if c=Vmin1then

15. c←Vmin1+1

3.4 查询操作

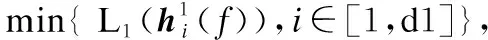
查询操作的伪代码如算法2所示.

算法2.Double sketch查询操作

输入：f to query

输出：resultVquery

2.Vmin1←min(S1)

4.Vmin2←min(S2)

5.ifVmin2=0

6.Vquery←Vmin1

7.else

8.Vquery←Vmin1+Vmin2*2b1

9.returnVquery

3.5 测量任务

Double sketch可用来解决网络测量中的几种测量任务.

流大小估计：估计任何流量标识的流量大小.流标识可以是五元组的任意组合，如源IP地址和源端口，也可以是唯一的协议.在本文中，我们将一个流包含的数据包个数视为流的大小.

象流检测：在本文中指报告流数据包数量大于预定义阈值的流.

流频率估计：流频率估计对应本文中的流数据包数量估计.在本文中，插入操作在一个流标识为f的数据包到达时，将f的数据包数量加1；查询时，返回数据略图中估计的流数据包数量.对应的，在执行流频率估计时，每遇到一个标识为f的流，插入操作将其流频数增加1；查询时，数据略图返回流频率估计数.Double sketch在流频率估计与流包数估计上有相同的准确性与吞吐量，故实验部分并无详细区分.

2http：//www.caida.org/data/overview/

3http：//burtleburtle.net/bob/hash/evahash.html

3.6 性能分析

1)时间复杂度：数据包的插入过程决定了Double sketch算法的时间复杂性，在插入操作中哈希函数的计算量与内存的访问次数影响算法的时间复杂度.Double sketch算法包含两个CU原子数据略图的hash操作，执行一次插入时最好的情况下执行d1次哈希计算，最坏的情况下执行d2次哈希计算，d1、d2分别为L1层、L2层的哈希函数个数，均为常数，因此执行一次插入哈希部分时间复杂度为O(1)，执行一组数据流的插入操作哈希部分的时间复杂度为O(N)，其中N为数据包的个数.

2)空间复杂度：Double sketch算法的时间复杂性主要取决于两个CU原子数据略图的空间使用量，其所需内存为w1×d1×b1+ w2×d2×b2.

4 实验评估

4.1 实验装置

数据集：我们使用了从CAIDA收集的ip追踪流量数据2，此数据集包括11个.data二进制流文件，其中，每13字节的字符串是一个5元组(原ip地址；源端口；目的ip地址；目的端口；协议).每个流文件中约有2.5M个数据包，110K个独特流，每个流的数据包数量从1-17491不等，其中数据包数量为1的流约占29%.数据集参数如表2所示.

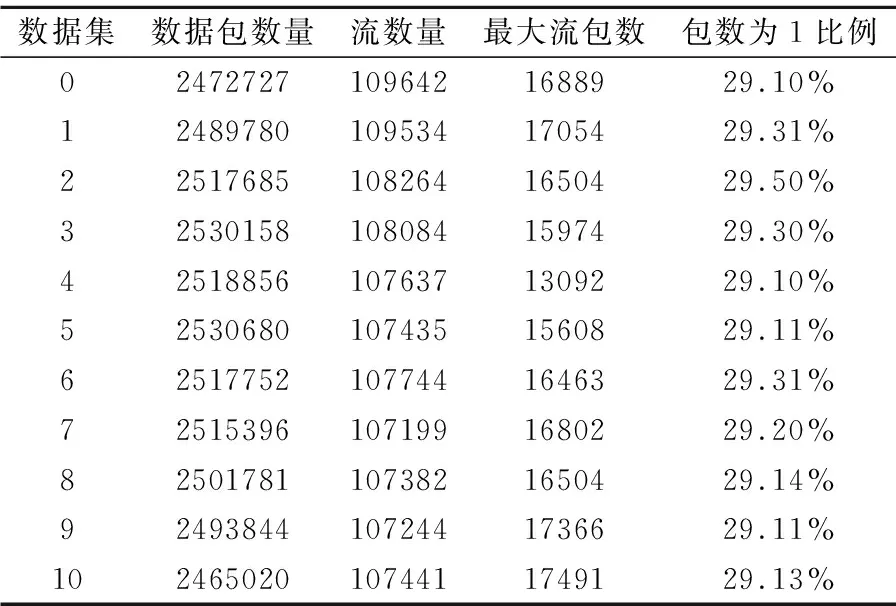
表2 不同数据集流数、包数统计表Table 2 Statistical table of stream number and packet number of different data sets

实现：我们使用c++编写程序，以执行CM、CU、Count、 Diamond sketch和double sketch的插入与查询操作.在我们的代码中，我们使用单核实现了单线程的数据结构.我们使用的哈希函数是从开源网站3获得的32位BOB哈希.

计算平台：我们在一台运行g++的8核CPU(11th Gen intel®coreTMi7-1165G7 @2.8 GHz)和16GB总动态内存的机器上执行了所有实验.CPU有三级缓存内存：每个内核共享两个320kb(1kb=210字节)的L1缓存，每个内核共享一个5mb的L2缓存，每个内核共享一个12mb(1mb B=220bytes)的L3缓存.

参数设置：我们将Double sketch与4个典型的数据略图进行比较：CM sketch、CU sketch、Count sketch和Diamond sketch.对于这5种数据略图，包括Diamond和Double数据略图中的原子数据略图，每个数据略图有3个32位的BOB哈希函数，对应每个略图有3个数组.为了适应上述数据集中出现出现的最大流的数据包数量，我们需要设置5种数据略图计数器的合适大小.我们将C、CU、count sketch计数器大小设置为16位；将Diamond sketch进位部分的原子略图的计数器大小设置为2位，增量部分的所有的原子略图的计数器大小均设置为8位；将Double sketch的L1层和L2层的原子sketch的计数器大小均设置为8位.在我们的实验中为了达到较高的准确性，Diamond sketch的增量部分使用4个原子数据略图，进位部分与增量部分内存使用量的比值设置为0.2.Double sketch的满包计数层L2与余包记录层L1的内存使用比值设置为0.25.

4.2 评估指标

数据略图的性能通常是通过在固定内存大小下的准确性和速度来评估的.本文采用平均相对误差(ARE)和正确率(Accuracy)作为流大小估计或流频率估计的准确性衡量标准，F1-score作为象流检测的准确性衡量标准，吞吐量作为速度的衡量标准.

1)平均相对误差(ARE)

ARE的公式如公式(1)所示：

(1)

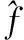
2)正确率(Accuracy)

Accuracy的定义如公式(2)所示：

(2)

其中n为被数据略图准确估计大小或频率的流个数，N为流的总数.

3)F1-score

F1-score是精确率和召回率的调和平均数，最大为1，最小为0，在本文中用于象流检测的准确性衡量.其公式如公式(3)-公式(5)所示：

(3)

(4)

(5)

其中，P为精确率，R为召回率，TP为预测且实际均为象流的流数，FP为错将非象流的流估算成象流的流数，FN为实际为象流而预测为非象流的流数.

4)吞吐量(Throughput)

吞吐量的公式如公式(6)所示：

(6)

其中c是数据略图中执行插入操作的数量，t为执行操作的总时间，MSPS是每秒一百万次的缩写.

4.3 准确性

在本节中，展示Double sketch和其他几个典型数据略图在CAIDA数据集上的ARE、Accuracy、F1-score的实验结果.

1)ARE

实验中，将5个数据略图的内存大小均设置为200kb.图2(a)绘制了不同数据略图在11组CAIDA追踪数据集上的ARE实验结果.由图2(a)可知，在内存大小固定为200kb时，Double sketch的ARE最小，分别比Count，CM，CU，Diamond sketch的ARE低5.64、3.62、2.46、1.27倍.

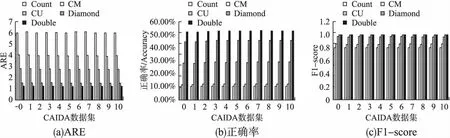
图2 CAIDA数据集ARE、Accuracy、F1-score比较Fig.2 ARE、Accuracy、F1-score comparison of CAIDA datasets

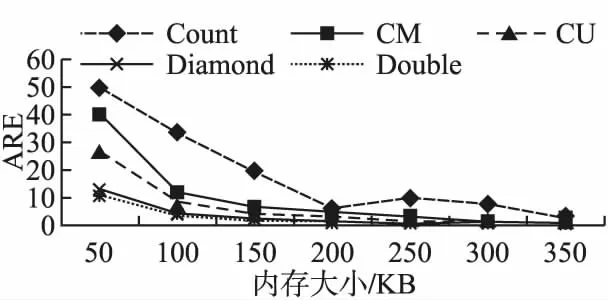
图3 不同内存ARE比较Fig.3 Comparison of ARE of different memory

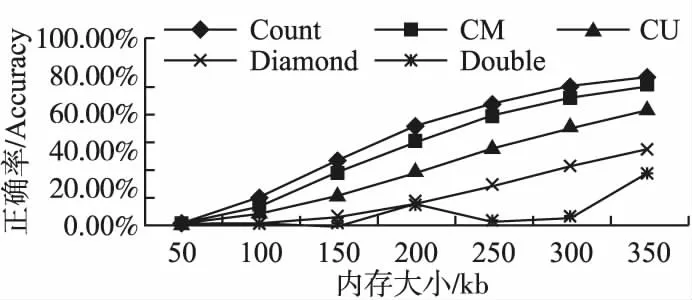
图4 不同内存Accuracy比较Fig.4 Comparison of different memory Accuracy

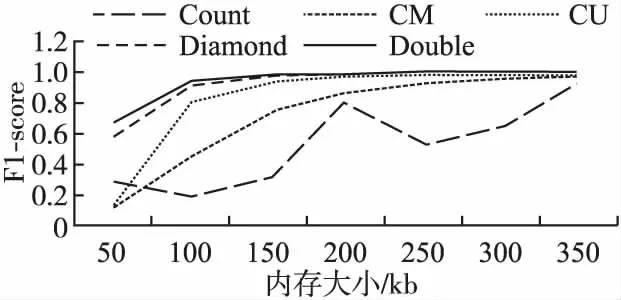
图5 不同内存F1-score比较Fig.5 F1-score comparison of different memory

2)Accuracy

由图2(b)所示，实验结果表明在内存大小为200kb时，对CAIDA追踪数据的11个数据集，Doubel sketch的正确率最高，是实验中唯一一个正确率大于50%的数据略图，分别约是Count，CM，CU，Diamond sketch的5.02、4.36、1.83、1.16倍.

3)F1-score

由图2(c)所示，在内存大小为200kb时，5种数据略图在11组数据集上的F1-score几乎相同，其中，Diamond sketch与Double sketch的F1-score值最接近1，为0.99，Count、CM、CU sketch的F1-score值分别为[0.79，0.8]、[0.85，0.86]、[0.96，0.97].因此，Double sketch和Diamond sketch对象流检测更为准确.

4)ARE随内存大小变化

在这一部分，通过改变数据略图所用内存大小，在CAIDA追踪数据集0上测试ARE的变化.实验内存大小从50kb到350kb，以50kb的步长增长.由图3可知，随着内存增大，数据略图的(Count sketch除外)ARE逐渐下降，在实验设置的内存中，无论内存多大，Double sketch的ARE均是最小的，即使在50kb的内存下，Double sketch的ARE也仅约为10.因此，在内存紧张的情况下，Double sketch是更好的方法.

5)Accuracy随内存大小变化

实验设置同ARE随内存大小变化相同.Accuracy随内存大小变化实验结果如图4所示.从图中可知，数据略图(Count sketch除外)的正确率随着内存的增加而升高.无论内存为多大，Double sketch的正确率均最高.

6)F1-score随内存大小变化

实验结果如图5所示，随着内存大小增加，数据略图的F1-score向1趋近，内存大小在[50，250]kb之间时，Double sketch的F1-score最接近1，到250kb时，Double sketch的F1-score已经达到了1.因此，在内存有限的情况下，Double sketch对象流检测更准确.

4.4 速 度

在本节中，展示Double sketch和Diamond sketch插入吞吐量的实验结果.

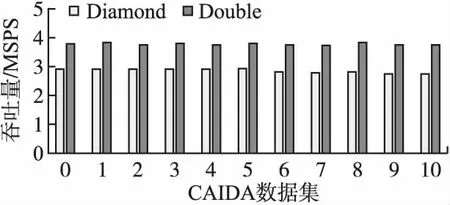
图6 CAIDA 数据集吞吐量比较Fig.6 Throughput comparison of CAIDA dataset

由图6所示，Double sketch和Diamond sketch在11组CAIDA追踪数据集上的插入吞吐量较稳定，Double sketch的吞吐量约为3.8MSPS，而Diamond sketch的吞吐量约为2.8MSPS.因此，Double sketch的速度比Diamond sketch的速度约快1.36倍.

5 结束语

数据略图是一种紧凑的数据结构，在流量测量领域有重要意义.在本篇文章中，我们提出了一个新的数据略图—Double sketch，包括余包记录层和满包计数层，动态记录流数据包数量，从而优化内存效率.我们已经将 Double Sketch与其他典型结构 Count sketch 、CM sketch、 CU sketch和 Diamond sketch 进行比较.实验结果表明，在保证速度的同时，在准确性上，我们的Double sketch数据略图有更好的表现.