自适应两阶段分组求解大规模全局优化问题
2023-01-31王宇嘉聂方鑫孙福禄
贾 欣,王宇嘉,聂方鑫,孙福禄
(上海工程技术大学 电子电气工程学院,上海 201620)
1 引 言
许多工程优化中涉及到数量庞大的参数问题、聚类问题[1,2]、特征选择问题[3,4],这类问题的特点是决策变量个数多,变量之间存在较强的相关性,称具有这类特点的问题为大规模全局优化(Large Scale Global Optimizations,LSGO)[5]问题.进化计算在低维问题求解中,取得了较好的效果,但是在求解LSGO问题时,往往会遭遇“维数灾难”,为了缓解维度灾难问题,研究者们提出了分治策略,即对一个LSGO问题首先进行分解,将其分解成多个低维问题,然后对分解后的低维问题分别进行求解.采用分治策略,缓解了维数灾难导致的进化算法性能下降的问题.
协同进化(Cooperative Coevolution,CC)[6]是采用分治策略解决LSGO的一般选择.协同进化算法(Cooperative Coevolution Evolutionary Algorithms,CCEAs)的难点是进行有效的分组[7,8],在处理LSGO问题时,由于决策变量之间相关性,使得CCEAs在分治求解的过程中并没有最优的方法将决策变量进行分组.
在CCEAs发展之初,静态分组和随机分组被广泛应用.Potter和De Jong[9]提出了静态变量分组算法(Cooperative Coevolution Genetic Algorithm,CCGA),该算法将LSGO问题的n个变量分解为n个一维的问题,通过GA对分解后的一维问题进行协同优化.Yang等人[10]提出随机分组的差分协同进化算法(Differential Coevolution Evolution random Grouping,DECC-G),DECC-G将LSGO问题的n个决策变量随机进行分组,通过DE对分组后的组件进行协同优化.CCGA和DECC-G在解决完全可分离的LSGO问题时取得了较好的优化结果,但在处理变量之间存在相关性的LSGO问题时,破坏了变量之间的相互作用,导致最终优化结果不佳.随后,研究者们提出了变量交互学习[11,12]分组方法,Omidvar等人[13]提出差分分组(Differential Group,DG),相比随机分组不考虑变量之间的相互影响,DG通过检测变量之间的相关性,将相互影响的变量分到同一组,增大组内变量相互作用,减少组间变量相互作用,提高了算法的优化性能.Mohammad等人[14]提出递归分组(Recursive Difference Grouping,RDG),RDG使用贪婪分解策略[15],将相互重叠的变量随机分配给与之交互的组件,提高了算法在处理变量重叠问题时的优化性能;但是DG和RDG在分组时仅考虑变量之间的相互作用,未考虑变量对适应度值的影响,所以降低了算法的收敛性.Philip等人[16]提出全局分组(Global Differential Grouping,GDG),首先对问题进行建模,然后采用微分分组策略对问题进行分组,提高了分组精度.Li等人[17]提出改善的差分分组(Effective Differential Grouping,DG2),该方法通过成对变量交互作用来估计舍入误差,提高算法分组精度.但是因为GDG和DG2增加了建模和估计误差操作,所以在分组时导致适应度评估次数和时间计算成本的增加.
为了克服以上的问题,本文提出了一种基于自适应两阶段分组的差分协同进化算法(Cooperative-Coevolution-DE with Two-StageGrouping in LSGO,DECC-TSL)来求解大规模全局优化问题.该算法通过两个阶段对变量进行分组操作,在第1阶段分组中,判断决策变量贡献度正负性,将其分为正促进组和负抑制组.在第2阶段分组中,分别对两组内的变量进行相关性的识别,统计并记录每个变量与之直接相关的变量个数,根据相关变量个数所占比例,确定组内变量个数.由于分组时增加了变量对函数贡献度的正负性判断,因此可以更好的避免将两个正负性相反的变量分到同一组内.在整个演化过程中,采用差分协同进化框架,使算法能快速地向问题的最优解方向收敛,有效地提高算法性能.
2 相关工作
2.1 大规模全局优化问题
在优化算法的发展初期,含有几十或上百个决策变量的问题被认为时LSGO问题,但随着优化问题复杂性的提高,现在一般认为存在上千个决策变量的问题为LSGO问题.LSGO问题可以描述为:
(1)
其中,f表示目标函数,x1,x2,…,xn表示决策变量,n表示决策变量的个数.
2.2 变量分离问题
定义变量分离问题[18]建立在变量相互依赖的基础上,变量的相互依赖性由公式(2)定义:
(2)
定义1.(直接相关作用):给定一个n维函数f(X)X=(x1,x2,…,xn),n≥2,当且仅当满足公式(2)时,xp和xq(1≤p≤q≤n)互为直接相关作用.
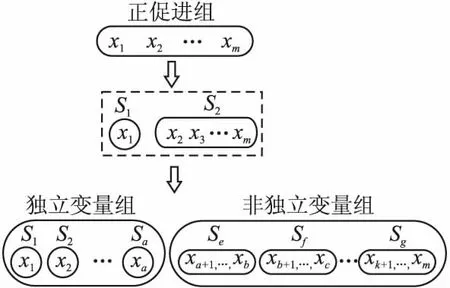
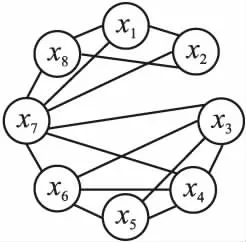
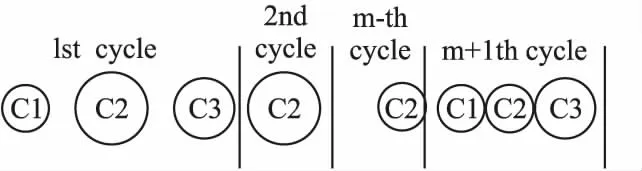
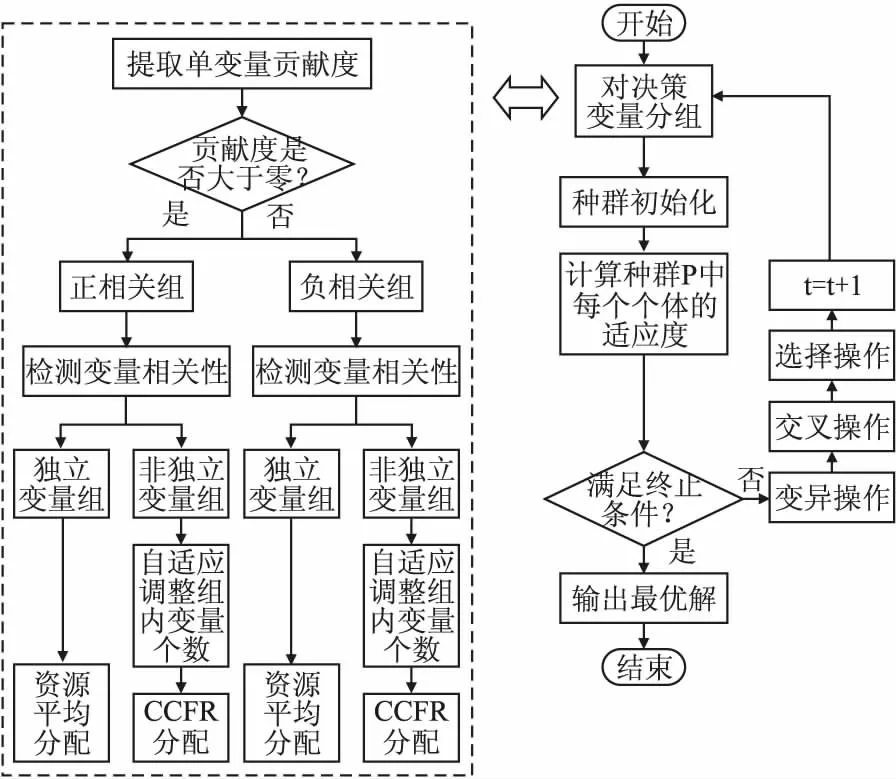
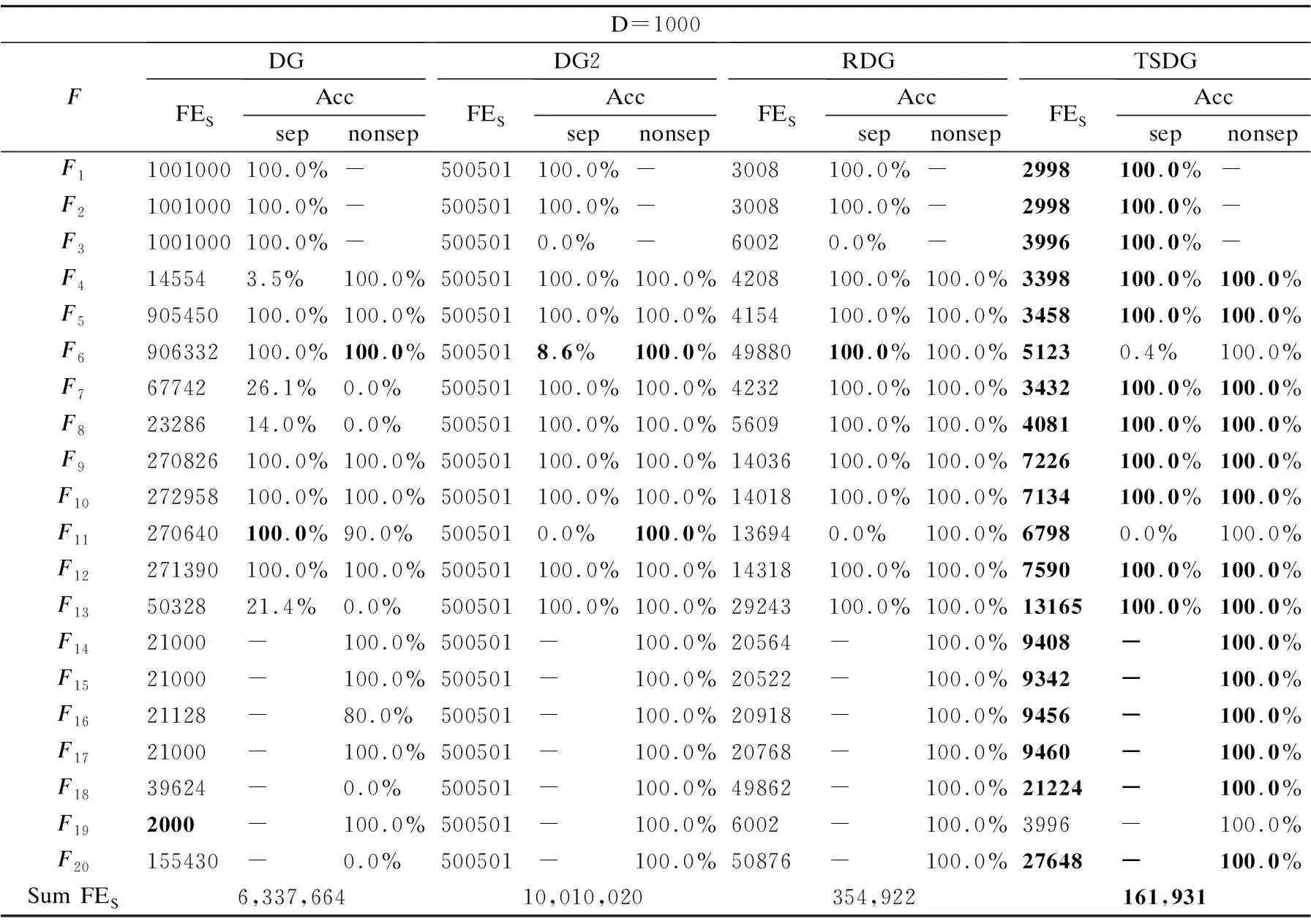
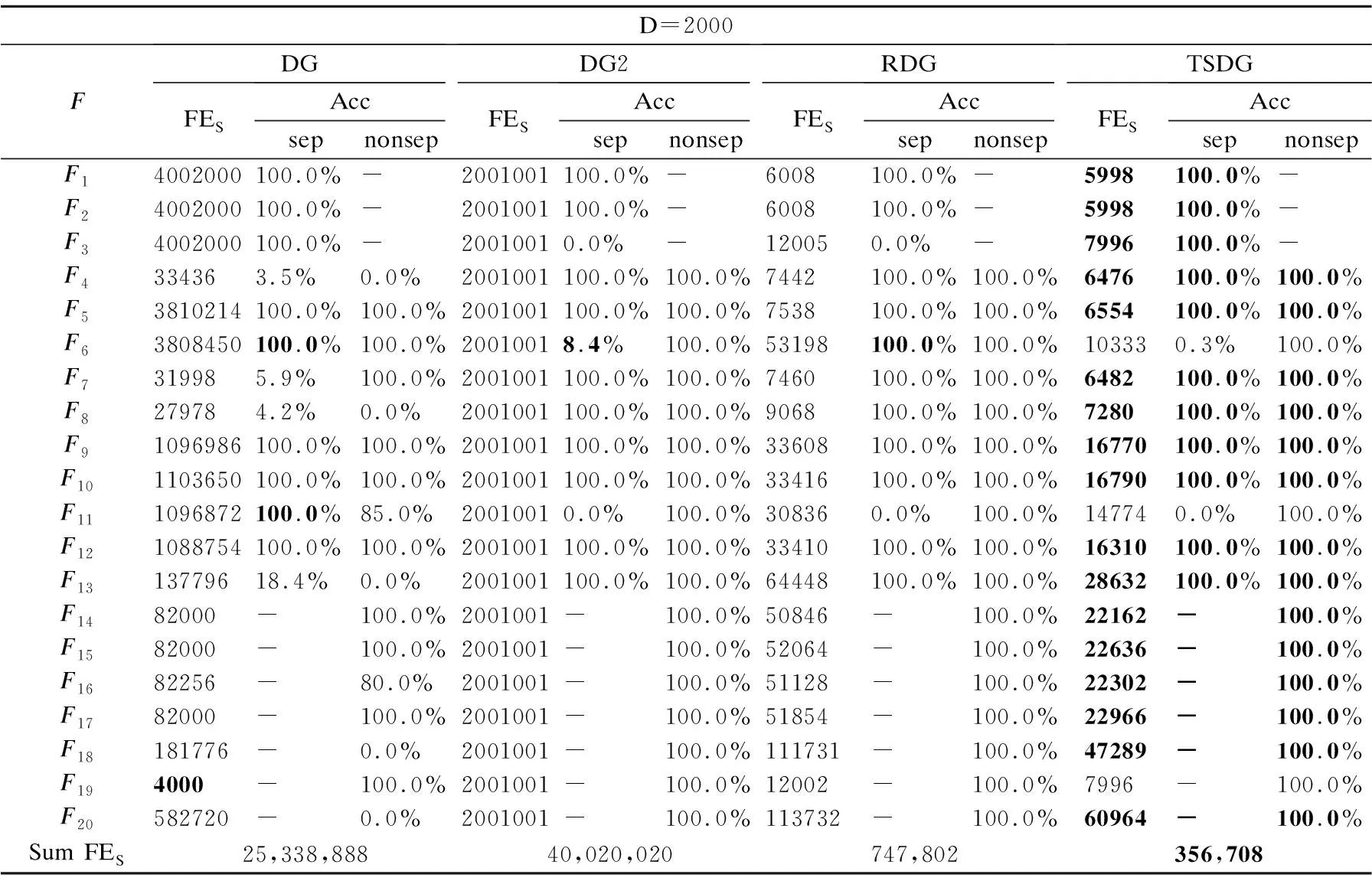
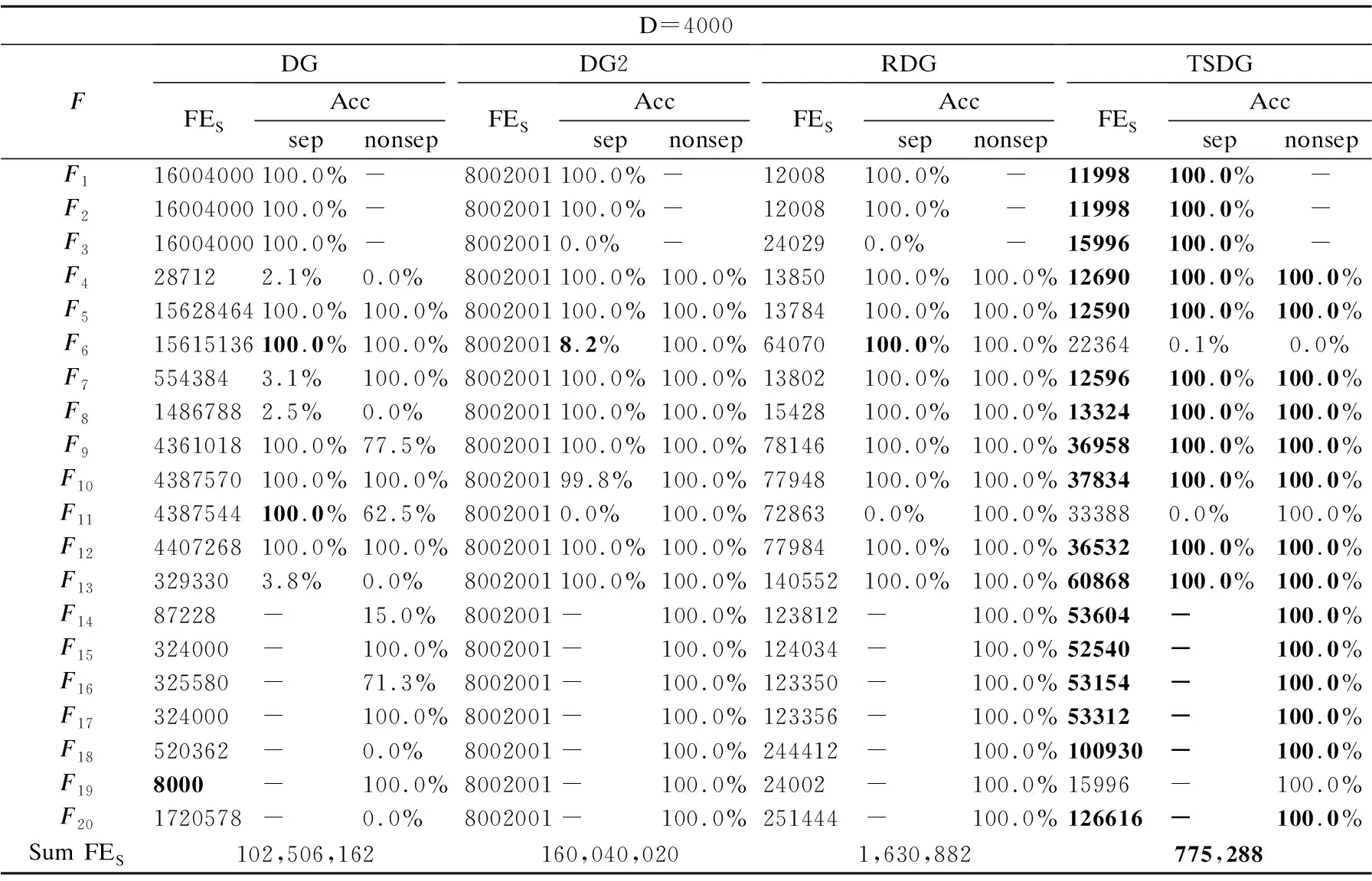
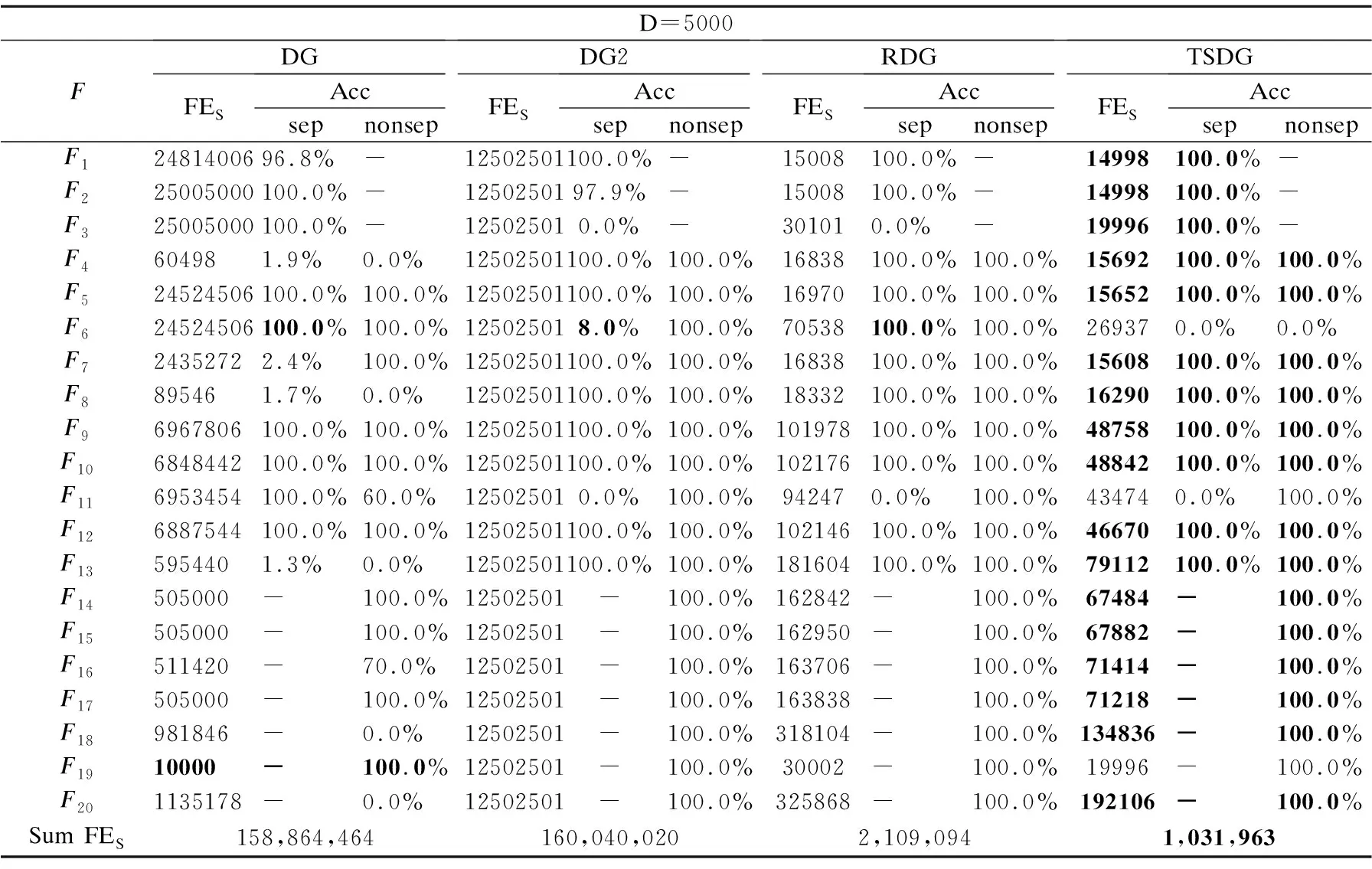
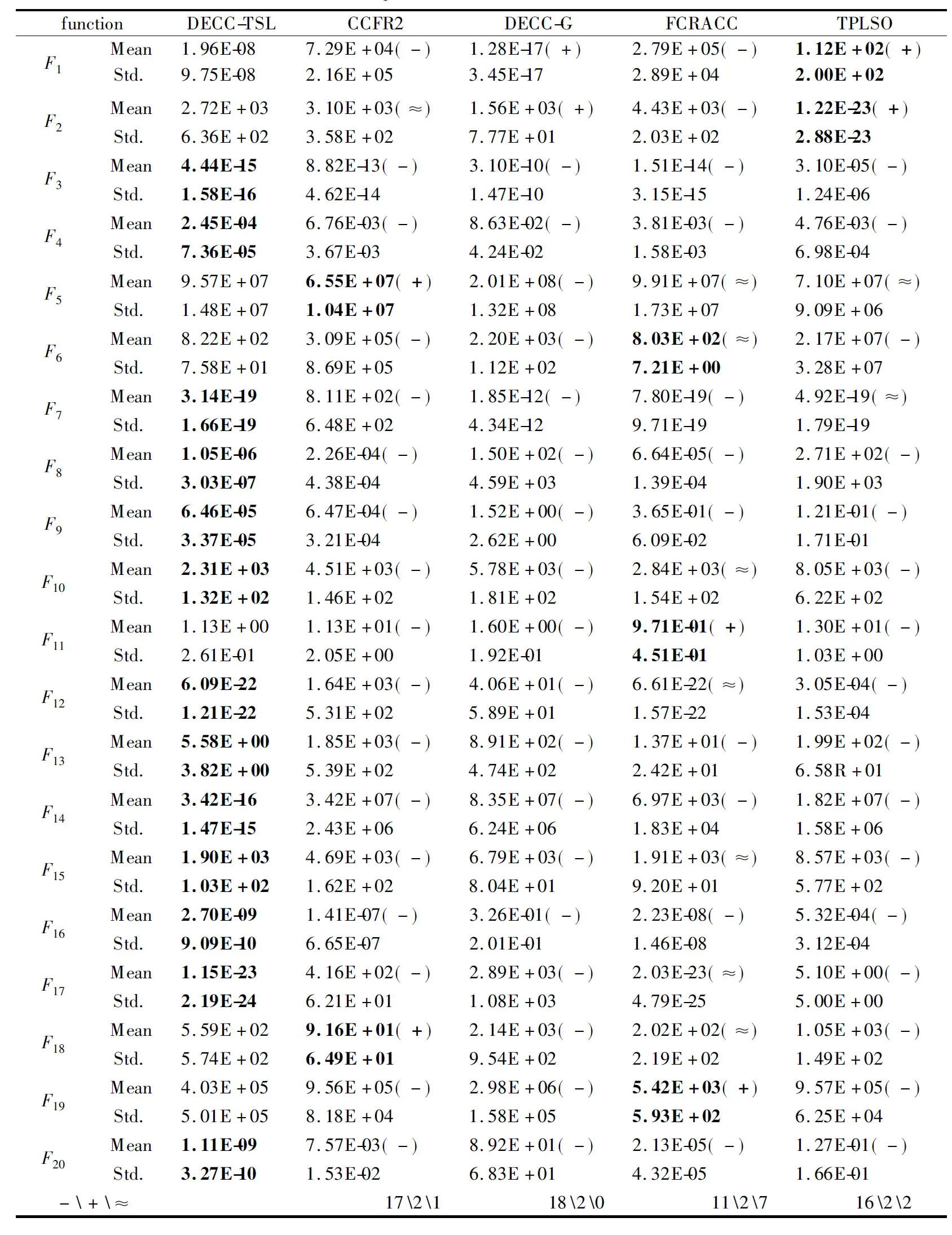
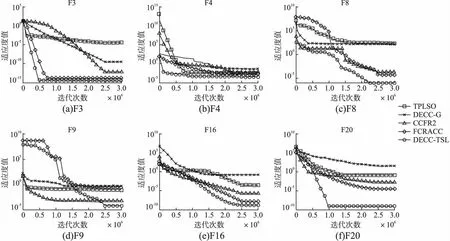
定义2.(间接相关作用):给定一个n维函数f(X),X=(x1,x2,…,xn),n≥3,当且仅当它们没有直接相互作用且存在子集合Θ,Θ⊂X,Θ=(x1,x2,…,xm),0 定义3.(独立变量):给定一个n维函数f(X),X=(x1,x2,…,xn),n≥2,当且仅当xp和xq既不存在直接相关作用也不存在间接相关作用时,xp和xq为独立变量. 根据上述3种定义,可以将LSGO问题大致分为两类,分别为可分问题和不可分问题. 定义4.(可分问题):当∃p,q∈{1,2,…n},p≠q,xp和xq为独立变量,则函数f(X)是可分问题. 定义5.(不可分问题):当∀p,q∈{1,2,…n},p≠q,xp和xq之间存在直接或者间接相关作用,则函数f(X)是不可分问题. 以变量为节点,直接相关作用为边,每对变量之间的相关性如图1所示. 图1 大规模问题分类 根据以上定义,图1(a)和图1(b)分别表示部分可分离函数和完全可分离函数;图1(c)是含有重叠变量的不可分离函数;图1(d)是完全不可分离函数. 差分进化算法(Differential Evolution,DE)[19]采用了遗传算法的基本框架,设计了独特的差分变异算子. 2.3.1 初始化 初始化种群: (3) (4) 其中,t代表迭代次数,dim代表问题的维数.当前迭代中的解x为目标向量.初始化之后,优化过程主要有3个步骤:变异、交叉和选择. 2.3.2 变异 变异产生的解称为供体载体v.有5种常见的突变策略,它们具有不同的差异载体. (5) (6) (7) (8) (9) 其中,r1、r2、r3、r4和r5是从[1,NP]中随机选择的,xbest是第t代中的最佳解.突变的形式可以表示为DE/a/b,其中′a′表示要扰动的向量,而′b′表示扰动向量′a′的差向量的数量. 2.3.3 交叉操作 对变异产生的供体载体v进行交叉操作,交叉产生的向量为m,在交叉过程中,供体载体向量和v决策变量x以概率CR随机选择. (10) 其中,qrand是从[1,dim]中的一个随机整数,用来保证变量中至少有一个向量进行了交叉操作.交叉概率CR∈[0,1]. 2.3.4 选择操作 选择操作判断是否可以将交叉向量m或目标向量x迭代到下一次popt+1中. (11) 其中,f(·)表示最小化问题中的目标函数. 3.1.1 变量贡献度 基于贡献度的分组策略,是一种根据变量收敛程度而进行分组的策略.所谓变量贡献度,是每个变量在迭代过程中,使适应度值减小的程度,变量贡献度计算过程如公式(12)所示,随机生成的适应度值作为变量贡献度的初始值. (12) 其中,xi表示第i个变量;t表示迭代次数;bi,t表示变量i在第t次迭代时的最佳变量;f(x|xi=bi.t)-f(x|xi=bi.t+1)表示两次迭代适应度的差值. 3.1.2 贡献度分组 通过对决策变量贡献度的计算,考虑到决策变量可能会对函数适应度值的改变具有正促进或负抑制的作用,如果把作用相反的两个变量分到同一组内,适应度值可能会由于相互抑制,而不能朝着最优解的方向进行.针对这个问题,在第1阶段分组时,判断所有变量的Fxi,将Fxi>0的变量分到正促进组,Fxi<0的变量分到负抑制组.第1阶段变量贡献度分组过程如图2所示. 图2 第1阶段分组Fig.2 First stage grouping 3.2.1 变量相关性 在优化问题中,决策变量之间相互作用,称这样的变量具有相关性.变量相关性由公式(13)和公式(14)表示: Δδ,xpf(x)|xp=a,xq=b≠Δδ,xpf(x)|xp=a,xq=c (13) Δδ,xpf(x)=f(…,xp+δ,…)-f(…,xp,…) (14) 其中,a,b,c代表不同的实数,δ代表对xp的扰动,且δ≠0,当xq取不同数值时,若对决策变量xp进行δ扰动导致适应度值发生变化,那么变量xp和xq具有相关性,称xp和xq互为非独立变量. 3.2.2 变量相关性识别 在第2阶段分组中,分别对正促进组和负抑制组内变量进行变量识别,分为独立变量组和非独立变量组. 图3 变量相关性识别Fig.3 Variable correlation recognition 第2阶段变量相关性识别过程如图3所示,以正促进组为例,具体步骤如下: Step1.从正促进组选取x1作为被检测变量,将其存入名为s1的变量组中,剩余变量存入名为s2的变量组; Step2.从s2中选择变量x2,根据公式(13)-公式(14),检测x1和x2的相关性; Step3.若x1与x2相关,则将x2放入s1中,若不相关,x2放入原变量组中; Step4.从s2中依次选取变量与x1进行相关性检测,重复Step 2-Step 3;直到x1与s2中m-1个变量完成相关性识别; Step5.若x1与s2中m-1个变量均不相关,则将x1放入独立变量组中,否则,将s1放入非独立变量组; Step6.重复上述Step 1-Step 5,直到将m个变量分别放入独立变量组和非独立变量组. 3.2.3 确定组内变量个数 通过变量相关性的识别,将所有变量分为独立变量组和非独立变量组.对于非独立变量组,变量之间存在相互作用,若组内变量个数过多,容易导致算法收敛性不佳.针对这个问题,在固定分组和随机分组策略中,均是提前定义好组内变量个数,然后进行分组.该策略易使算法陷入局部最优而无法跳出,最终导致算法无法找到最优解.本文提出一种自适应确定组内变量个数大小的差分分组策略(Two-stage Differential Grouping,TSDG),该策略选取变量所占比例较高的组内变量个数为分组大小,确定组内变量个数.当算法陷入局部最优时,该策略通过自适应调整组内变量个数,使算法跳出局部最优. 如图4所示8个变量为例,以变量为节点,直接相关作用为边,与x1,x2,x5,x8直接相关的变量有3个,占总变量1/2;与x3,x4,x6直接相关的变量有4个,占总变量3/8;与x7直接相关的有6个变量,占总变量1/8.所以首先选择分组大小为每组4个,以组内贡献度最大原则进行变量的分组.在迭代过程中,算法由于陷入局部最优而无法跳出时,通过自适应调整组内变量个数,形成自适应的分组策略.使算法跳出局部最优. 图4 分组策略Fig.4 Grouping strategy LSGO问题分组后,相比分组之前,组件的数量会变多.目前,将计算资源平均分配给每一个组件是较为方便的一种策略,但是每一个组件对适应度值的影响程度不同,若采用平均分配计算资源给每一个子组件,会使贡献度较高的组件和贡献度低的组件分配一样的计算资源,显然这种分配策略是不合理的.为了解决计算资源均匀分配的不足,本文主要采用CC算法下有效的资源分配(Resource Allocation in CooperativeCo-Evolution,CCFR)[20].CCFR采用公式(15)计算组件贡献度,根据组件在最近两次迭代中的平均贡献度来分配计算资源. (15) 其中,fb和fbi分别表示组件ci在上一次迭代和当前迭代的最佳适应度值,Fci是组件在上一个迭代的贡献值. 图5 自适应资源分配Fig.5 Self-adaptive resource allocation CCFR资源分配过程如图5所示,假设该问题包含3个组件,图中每一个圆代表一个组件,圆的大小表示贡献度大小.具体步骤如下: Step1.在初始阶段,根据公式(15)计算3组件的初始贡献度; Step2.在第2阶段选择最大贡献度组件C2,分配计算资源; Step3.循环Step 2,判断C2贡献度是否小于C3; Step4.若小于,在下一阶段选择此时最大贡献度组件C3,分配计算资源; Step5.循环Step 2-Step 4,当算法达到最大迭代次数时,算法停止. DECC-TSL算法流程如图6所示.它与传统的协同差分分组算法主要有两个不同之处:1)在第1阶段分组,判断变量贡献度的正负性,避免贡献度值相反的变量分到同一个组件中;2)在变量相关性识别中检测出非独立变量组,选取变量所占比例较高的组内变量个数为分组大小,确定组内变量个数.在整个优化过程中,通过自适应的调整组内变量的个数,避免算法陷入局部最优.DECC-TSL算法具体步骤如下: 图6 自适应两阶段差分分组算法流程图Fig.6 Flow of adaptive two-stage differential grouping algorithm Step1.根据公式(12)对变量贡献度FX进行计算; Step2.判断FX的正负性; Step3.若FX>0,则将该变量分到正促进组,反之进入负抑制组; Step4.根据公式(13)和公式(14),分别对正相关组和负相关组内的变量进行变量相关性检测; Step5.依次选取变量作为被检测变量,判断被检测变量和剩余变量之间是否存在相关性; Step6.若存在,将相关变量与被检测变量放置在同一个组件内.若不存在,则将被检测变量放在独立变量组内; Step7.重复Step 5、Step 6,直到所有变量分到独立变量组和非独立变量组; Step8.对于非独立变量组,选取组内数量比例较高的一组作为组内变量个数,自适应的调整组内变量个数; Step9.在资源分配阶段,给独立变量组中每个变量分配相同的计算资源进行优化,对非独立变量组采用CCFR资源分配,在每次进化周期中,选择对适应度值贡献度最大的组件进行优化; Step10.重复Step 8、Step 9,直到达到函数的最大评估次数,算法停止. 本文采用标准测试函数集CEC2010[21]验证算法的有效性.CEC2010函数集一共包含20个测试函数,依据变量的不同性质,可以将20个测试函数分为4大类: 1)F1-F3:此函数只包含独立变量,称该函数为完全可分离函数; 2)F4-F13:此函数同时包含独立变量和非独立变量组,称该函数为第1类部分可分离函数; 3)F14-F18:此函数同时包含多个非独立变量组,称该函数为第2类部分可分离函数; 4)F19-F20:此函数仅包含一个非独立组,称该函数为完全不可分离函数. 为了验证所提分组策略的有效性,利用CEC 2010测试集提出的20个测试函数对TSDG的性能进行研究.将TSDG与DG、 DG2、RDG分别在D=(1000,2000,3000,4000,5000)维下进行对比. 两个指标用于评价分组方法的性能:用于分解问题的函数评估的数量(FEs)和分组精度(Acc).FEs个数越少,Acc越高,则分组方法的性能越好. 分组方法的分组精度定义如下: (16) (17) 其中,sep代表函数包含可分变量的总数,nonsep代表函数包含不可分变量的总数,sep′和nonsep′分别代表真正正确识别出的可分变量和不可分变量. 如表1-表5所示,分别为TSDG在1000-d、2000-d、3000-d、4000-d、5000-d下与其他3种策略的对比结果.在分组精度上与其他策略对比,所提出的TSDG可以正确地分解除F6、F11之外的其他测试函数;在函数评估数量上与其他策略对比,仅F19在DG使用的评估次数少于TSDG,在其他19个函数上TSDG使用的FEs最少. 如表1所示1000维下TSDG与其他3种策略对比,针对分组精度,与DG相比,DG虽然在F6和F11上分组准确率略好于TSDG,但在F4、F7、F8、F13、F18函数上TSDG分组准确率高于DG;与DG2、RDG相比,虽然DG2、RDG在F6可分变量上分组精度略高于TSDG,但是DG2在F6上使用的FES是TSDG的100多倍,RDG在F6上使用的FES是TSDG的10多倍.此外,TSDG在F3上能进行正确的分组,但DG2、RDG则不能.在剩余函数分组精度相同时,对比FEs,DG除了在F19上使用的FES略少于TSDG,在其他函数上使用的FES均高于TSDG,尤其是在完全可分离的函数F1-F3上,DG使用的FES是TSDG的300多倍;与DG2和RDG相比,TSDG使用的FES远少于DG2和RDG使用的FES,这是因为TSDG在变量识别时,分别对正促进组和负抑制组两组内变量同时进行识别,极大地减少了FEs在时间上的成本. 表1 CEC2010测试集在1000维上分组结果Table 1 Grouping results on the 1000-d CEC2010 functions 如表2所示2000维下TSDG与其他3种策略对比,在分组精度上与1000维结果一样,但是随着维度的增加,变量之间的相关性更加复杂,使得DG在F4、F7、F8、F13、F18函数上分组精度相比于在1000维上的分组精度减少,导致分组精度下降.在分组精度相同的函数中,对比FES,TSDG使用的FES远少于其他3种策略使用的FES.与DG相比,在完全可分函数F1-F3上,DG使用的FES是TSDG的600多倍,在部分可分函数上,DG使用的FES同样高于TSDG使用的FES;与DG2相比,在可分离函数上DG2使用的FES是TSDG的300多倍,在部分可分离函数上,DG2使用的FES同样高于TSDG使用的FES;与RDG相比,在可分离函数上RDG使用的FES略高于TSDG,但在部分可分离函数上,RDG使用的FES是TSDG的2-3倍;由此可见随着维度的不断增加,DG、DG2和RDG使用的FES远远高于TSDG使用的FES,且成倍数增加趋势. 表2 CEC2010测试集在2000维上分组结果Table 2 Grouping results on the 2000-d CEC2010 functions 同上述分析一致,表3-表5分别为TSDG在3000-d、4000-d、5000-d下与其他3种策略的对比结果.随着维度的增加,由于变量之间的相关性更加复杂,导致分组精度下降、FES增加. 表3 CEC2010测试集在3000维上分组结果Table 3 Grouping results on the 3000-d CEC2010 functions 表4 CEC2010测试集在4000维上分组结果Table 4 Grouping results on the 4000-d CEC2010 functions 表5 CEC2010测试集在5000维上分组结果Table 5 Grouping results on the 5000-d CEC2010 functions 但是TSDG在更高维度下测试20个函数,仍然能将18个测试函数进行正确分组,同时TSDG在19个测试函数上使用了更少的FES.综上所述,TSDG可以用更少的FEs将大部分测试函数的可分离变量和不可分离变量能进行正确的分解,TSDG性能更好. 4.2.1 对比测试算法 为了分析所提算法的收敛速度和收敛精度,将提出的DECC-TSL算法与两阶段学习的粒子群算法(TPLSO)[22]、改进的资源分配协同算法(CCFR2)[23]、随机分组的差分算法(DECC-G)[24]、基于贡献度分组策略(FCRACC)[25]、进行仿真对比.其中,3个算法采用了不同的分组策略进行优化求解,具体区别如表6所示. 表6 算法分类描述 4.2.2 实验结果分析 在实验对比中,测试问题维度D=1000,函数的最大评估次数FEs=3×106,实验中每一个算法对于每一个测试函数均独立运行25次.DECC-TSL算法种群大小N=50,分组阈值ξ=50.实验结果如表7所示,部分收敛曲线如图7所示. 为了更直观的了解DECC-TSL算法的性能,采用Wilcoxon秩和检验,对实验结果进行统计分析,显著性水平为0.05.秩和检验结果在表7底部用符号“-”、“+”和“≈”表示,分别表示劣于、优于和相当于DECC-TSL的结果. 表7和图7分别为改进算法与其他4种算法的对比结果和对照图.其中,“Mean”和“Std”是每一个测试函数25次独立运行后所获得的平均值和标准差,黑体字的值表示算法获得的值在对应测试函数上是最好的.从表7中我们可以看到在测试函数F3、F4、F7、F8、F9、F10、F12、F13、F14、F15、F16、F17、F20上,本文提出的DECC-TSL算法性能明显优于其他4种算法.在20个测试函数上,DECC-TSL算法性能仅在完全可分离函数F1、F2上优化性能次于DECC-G和TPLSO,而在剩余18个测试函数(包含部分可分离函数和完全不可分离函数)都优于DECC-G和TPLSO,这是因为TPLSO采用无分组的竞争学习策略,算法容易陷入局部最优,而DECC-G采用随机分组策略,破坏了变量之间的相关性,导致算法收敛性降低,而DECC-TSL通过两阶段分组,考虑变量之间相关性,提高了算法的收敛性.有效的避免算法陷入局部最优. 表7 测试函数仿真结果 图7 各算法对比收敛图Fig.7 Algorithms convergence graph 与CCFR2算法对比,虽然DECC-TSL和CCFR2在进化过程中均采取了分治策略,但是DECC-TSL仅在F5、F18两个函数上优化性能次于CCFR2,在剩余17个测试函数(F2除外,在F2函数上两种算法表现相似)都要优于CCFR2.这是因为CCFR2是对种群进行的随机分组,未考虑变量之间的相关性,DECC-TSL通过检测变量之间相关性,将其分为独立变量组和非独立变量组,在资源分配时,分别采用不同分配策略,使算法更加具有有效性和适用性. 与FCRACC算法对比,因为两个算法均对变量进行多次分组的操作,所以从实验结果看出,对于部分函数,两个算法最终收敛结果相差不大.但是DECC-TSL在F1、F2、F3、F4、F7、F8、F9、F11、F16这9个函数上优于FCRACC.这是因为FCRACC仅考虑变量贡献度的大小,而DECC-TSL考虑变量贡献度对函数适应度值的正负性影响,避免将具有相反贡献度的变量分为一组,从而提高了算法的收敛性. 分析表7底部Wilcoxon秩和检验的统计结果,DECC-TSL算法相比于其他4种算法显示出更好的优势.综合以上分析可以说明DECC-TSL算法与文中其他4种算法相比,具有较强的收敛性和适用性,在解决LSGO问题时,提高了算法的性能. 目前协同进化是解决大规模全局优化问题的一种有效策略,但是在处理变量之间存在相互作用的LSGO问题时,现有的协同进化分组机制不能进行有效的分组,最终导致算法优化性能不佳.针对这一情况,本文提出一种基于自适应两阶段分组的差分协同进化算法.该算法通过对决策变量进行变量贡献度的提取并判断其贡献度的正负性,利用正负性进行第1阶段分组,分为正促进组和负抑制组;然后分别对两组内的变量进行变量相关性的识别,统计并记录每个变量与之直接相关的变量个数,确定组内变量个数.为了验证算法的有效性,通过实验将本文提出的DECC-TSL算法与TPLSO、CCFR2、DECC-G、FCRACC 4个算法进行对比,通过20个Benchmark测试函数,实验结果验证了DECC-TSL算法在求解LSGO问题上,提高了算法的收敛性和有效性.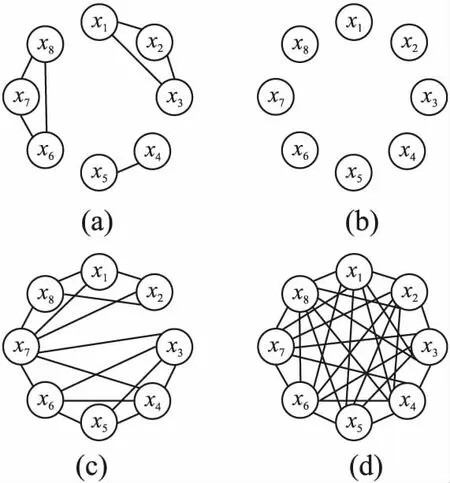
2.3 差分进化算法
3 算法框架
3.1 第1阶段分组
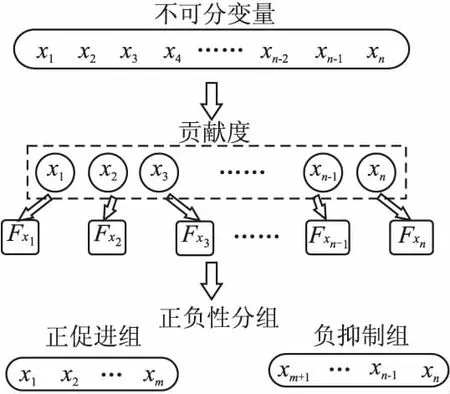
3.2 第2阶段分组
3.3 资源分配
3.4 基于自适应两阶段分组的差分协同进化算法
4 仿真结果与分析
4.1 分组有效性分析

4.2 DECC-TSL收敛性分析

5 结 论
