数学教学中应注意以启促思、以思促悟*

戴 悦

“启·悟”课堂是指以教师的“启”为手段，以学生的“悟”为目的，通过教师适时适度的“启”，助推学生对表层的数学信息进行加工内化，促进他们深度地思考、透彻地感悟。情境“启·悟”、问题“启·悟”、经验“启·悟”、实践“启·悟”等是小学数学“启·悟”课堂常用的几种方式，有助于学生通过观察、分析、比较、思辨悟出数学本质、数学思想、数学价值。

1.情境“启·悟”，培养学生多元思维能力

在教学中创设情境，有助于激发学生的学习兴趣，促使他们在课堂中自由地表达，放飞求异思维的翅膀，培养多元思维能力。例如，在教学苏教版五下《解决问题的策略：转化》一课时，教师可以通过故事导入引发学生思考：同学们看过赛马吗？赛马时一般都是比谁的马跑得快。可是，有这样一对兄弟，他们赛马时比谁的马跑得慢，谁的马最后到达终点谁就赢。兄弟俩比赛时总是想让自己的马跑得越慢越好，天都快黑了还没分出胜负来。这时，一位头发花白的老人对兄弟俩说了一句话，兄弟俩立刻就骑着马飞奔起来，很快就分出了胜负。你知道老人对兄弟俩说了一句什么话吗？学生由兴奋到疑虑，到分析，到讨论，到顿悟：兄弟俩换马骑了。教师追问：为什么换马骑时他们就要飞奔起来呢？学生纷纷表达自己的想法：比赛的规则没变，只是现在兄弟俩分别骑着对方的马，当然都希望让对方的马跑得快一些，谁骑着对方的马最先到达终点，谁就赢了。教师趁机引入课题：这种转化的策略对我们的数学学习有什么启发呢？生动有趣的故事情境唤起了学生学习的积极情感，使他们深度投入学习过程中，这其中有理解、有辨析、有推理、有发现，发展了学生的多元思维能力。

2.问题“启·悟”，推动学生进行深度学习

问题是数学“启·悟”课堂的启动器。教师应注意依据教学内容设计能体现数学本质的核心问题，并以此作为引领学生深入思考的课堂主线，带动学生展开多维度的思考，逐步将学生的思维引向深入。例如，教学苏教版五下《圆的认识》一课时，教师创设了如下问题情境：三只小动物正骑着不同形状车轮的自行车比赛呢。同学们猜一猜，谁会赢？为什么会是小兔子赢呢？我们生活中的自行车车轮为什么要做成圆的？圆作为平面图形中最美的图形，有哪些特征呢？上述问题的提出，由猜问到启问再到自问，激起了学生对圆的思考与探究，促进他们的思维向理性化、科学化升华，驱动其在画圆、剪圆、折圆的过程中探究圆的特点。

3.经验“启·悟”，促进学生感悟知识本质

数学学习是学生基于已有经验主动建构知识结构的过程。在教学中，教师应注意引导学生结合已有经验，找准认知起点，打通已知和新知之间的内在联系，启发学生在深度思辨中理解和构建知识，感悟知识本质。例如，教学苏教版六上《比的认识》一课时，教师提问：“比”在你们心中长什么样？接着让不同的学生配制不同比例的糖水，分别为1∶8、10∶80、20∶160。在学生初步理解“比”的知识、建立“比”的概念之后，出示：从北京到上海的路程大约是1500千米，一列高铁行驶了5小时。在学生写出1500∶5之后追问：这是“比”吗？它是什么意思？还可以怎样写？学生通过讨论、交流，发现1500∶5反映的是路程和时间的关系，也可以写成除法式子1500÷5，其计算结果就是速度。这里的“比”不仅表示一种倍数关系，还表示两个量度量的结果，这其实就是“比”的本质。上述教学中，教师“有结构地教”，启发学生“有关联地学”，不断丰富学生对“比”的认识，使他们不但知道了“比”是从除法、份、倍、分数中来的，还找到了“比”这一概念的生长点和延伸点。

4.实践“启·悟”，助力学生领悟思想方法

开展数学实践活动，让学生在动手、动口、动脑的过程中发现、提出、分析和解决问题，能使他们对数学知识和规律有真切的体会，对数学思想方法有深刻的感悟。例如，《解决问题的策略：转化》一课有如图1所示的一道习题，要求学生用分数表示各图中的涂色部分。当教师问学生第三个图形用什么分数来表示时，学生异口同声说出“十六分之九”。他们认为：绕着一个顶点旋转，正好和9格一样大，整个图形16格，所以涂色部分是整个图形的十六分之九。这是学生在观察和想象基础上形成的直观判断。为了让学生真切地感受到自己的判断有误，教师要求他们通过动手画一画、剪一剪来验证。学生通过动手操作，发现涂色部分比原来的9格还要多一些，逐渐有了困惑和思考：将图中涂色的部分直角三角形进行平移，这样涂色部分正好是10格，占整个图的十六分之十。还有学生想到把4个空白的直角三角形合起来正好是6格，这样涂色部分就是10格，用分数表示也是十六分之十。如此，学生体验得更深刻，尤其是在活动过程中将转化的思想方法直观化，加深了他们对数学思想方法的理解。

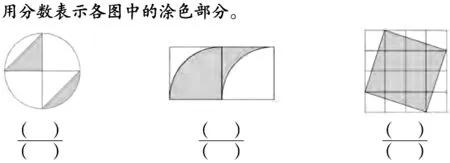
（图1）

总之，在小学数学“启·悟”课堂中，教师应注意整体把握学生的认知水平和教学内容，以启促思，以思促悟，让学生充分经历探究过程，从而促进他们发展数学思维，培育核心素养。