以结构化教学化数学知识为数学素养*

王 翠

《义务教育数学课程标准（2022年版）》鲜明地提出了“结构化”的观点，从课程理念、课程目标到课程实施，“结构”一词出现了近二十次。可见，结构化教学已经成为新课改的重点，是学生核心素养培育落地的重要切入点。

数学是一门结构性很强的学科，但知识点被分散在一节节课堂中，很容易被视作数学知识和基本技能的简单堆砌和排列。结构化教学能打破这种碎片化的教学样态，它是指基于学生的认知经验和思维特点，用高观点、大视野和关系思维统摄多个独立而又具有关联的知识点，引领学生经历层次化、结构化、逻辑化、整体化的学习过程，通过主动迁移、彼此融合、抽象建模、整体架构等建构知识网络。

1.串联“知识点”，从具体经验上升为抽象经验

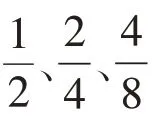
2.链接“方法群”，由点状探究转向整体建模

数学学习不能只停留于线性知识的习得，还要深入思想方法的“腹地”——方法关联。结构化教学倡导超越知识内容的局限，将不同领域的知识用相同的数学思想方法、策略等统整起来，生成方法（策略）结构，从而引导学生在更高层面通过整体建模来理解和应用数学方法（策略）解决问题。如教学苏教版五下《和与积的奇偶性》一课时，大多数学生都能通过列举验证猜想，但未能深入知识本质，难以举一反三，引导他们通过画图（如图1）来理解能起到“四两拨千斤”的作用。从图1中可以看出：奇数都单着一个，除以2都余1；偶数都成双成对出现，除以2没有余数。所以，当奇数和偶数相加时还会单着1个，即奇数+偶数=奇数；而当奇数和奇数相加时，两个单着的1就凑成了2，所以奇数+奇数=偶数；偶数和偶数相加，始终是成双成对的，所以偶数+偶数=偶数。学生通过图形建构的模型还可以应用于研究“多个数相加的和的奇偶性”“差的奇偶性”“积的奇偶性”等相关知识。在教学本课之后，教师还可以引导学生回忆“以前学习的内容哪些也是通过图形来解决问题的？”，从而有效联结学生潜意识里的“方法群”，如“乘法分配律”“间隔排列的规律”等，启发学生在后续学习中能自主想到运用画图的方法来解决问题。

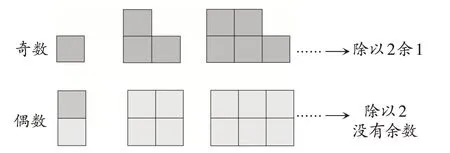
（图1）

3.统整“类教学”，将知识结构内化为认知结构

结构化教学主张从“类”的视角建构课，一方面，教师基于全局视野安排分散在教材中的散乱知识，重组优化，将一节课的“特殊性”延展为一类课的“一般性”；另一方面，学生探究知识形成的过程结构和逻辑，将习得知识的路径在更大范围内进行迁移与拓展，逐步形成联系的、发展的、辩证的眼光和思维方式。如教学苏教版五上《认识负数》一课时，笔者提出“你能用自己的方式表示对-2的理解吗？”这一问题，并组织学生展开探究。有的学生用温度计表示-2℃的含义，有的画图表示地下停车场-2层，有的表示海拔高度-2米……有文字表征，有画图表征，还有算式表征……虽然学生对“-2”的表征方法不同，但他们找到了“-2”背后共同的本质——比标准少2的数。以典型例子切入，以问题驱动，唤醒学生的已有经验，引导学生进行多元表征，建构属于他们自己的数学理解，这样的教学模式也适用于其他数的认识的教学。

总之，结构化教学通过梳理、归纳和整合，将离散、断裂、碎片化的知识连成线、结成网、筑成块、构成体，从而使学生看到知识发生、发展的全过程，习得重要的数学思想方法，探索出了思维生长的有效路径——从静态单一思维到动态辩证思维，从结果思维到过程思维，从简单思维到复杂思维，从借鉴、传承思维到质疑、批判、创新思维，真正彰显出数学学科独特的育人价值。